클러스터 분석

시리즈의 일부
기계 학습 및 데이터 마이닝
문제 분류 클러스터링 회귀 이상 검출 데이터 클리닝 자동 ML 어소시에이션 규칙 강화 학습 구조화된 예측 기능 엔지니어링 기능 학습 온라인 학습 준지도 학습 비지도 학습 순위 매기기 학습 문법 유도
지도 학습 (분류 • 회귀) 의사결정 트리 앙상블 배깅 부스팅 랜덤 포레스트 k-NN 선형 회귀 네이비 베이즈 인공신경망 로지스틱 회귀 분석 퍼셉트론 관련 벡터 머신(RVM) 서포트 벡터 머신(SVM)
클러스터링 버치 치유하다 계층적 k자형 기대 최대화(EM) DBSCAN 광학 평균 이동
치수 축소 인자 분석 CCA ICA LDA NMF PCA PGD t-SNE
구조화된 예측 그래픽 모델 베이즈 네트 조건부 랜덤 필드 히든 마르코프
이상 검출 k-NN 국소 특이치 계수
인공신경망 자동 인코더 인지 컴퓨팅 딥 러닝 딥 드림 다층 퍼셉트론 RNN LSTM GRU ESN 저장고 계산 제한 볼츠만 기계 GAN somerset. 컨볼루션 뉴럴 네트워크 유넷 트랜스포머 비전. 스파이킹 뉴럴 네트워크 메모리 트랜지스터 전기화학 RAM(ECRAM)
강화 학습 Q-러닝 사사 시간차(TD) 멀티 에이전트 셀프 플레이
인간과의 학습 액티브 러닝 크라우드 소싱 휴먼 인 더 루프
모델 진단 학습 곡선
이론. 커널 머신 바이어스-분산 트레이드오프 컴퓨터 학습 이론 경험적 리스크 최소화 오컴 러닝 PAC 학습 통계학 학습 VC 이론
기계학습장 NeurolIPS ICML ML JMLR ArXiv:cs.LG
관련 기사 인공지능 용어집 기계 학습 연구를 위한 데이터 세트 목록 기계학습의 개요
v t

클러스터 분석 또는 클러스터화는 동일한 그룹(클러스터라고 함)의 개체가 다른 그룹(클러스터)의 개체보다 서로 더 유사(어떤 의미에서는)하도록 개체 집합을 그룹화하는 작업입니다.탐색적 데이터 분석의 주요 업무이며, 패턴 인식, 이미지 분석, 정보 검색, 생물 정보학, 데이터 압축, 컴퓨터 그래픽스 및 기계 학습을 포함한 많은 분야에서 사용되는 통계 데이터 분석을 위한 공통 기술이다.

클러스터 분석 자체는 하나의 특정 알고리즘이 아니라 해결해야 할 일반적인 작업입니다.클러스터를 구성하는 요소와 클러스터를 효율적으로 찾는 방법에 대한 이해도가 크게 다른 다양한 알고리즘을 통해 이를 달성할 수 있습니다.군집의 일반적인 개념에는 군집 구성원 간의 거리가 작은 그룹, 데이터 공간의 밀도가 높은 영역, 구간 또는 특정 통계 분포가 포함됩니다.따라서 클러스터링은 다목적 최적화 문제로 공식화할 수 있습니다.적절한 클러스터링 알고리즘과 파라미터 설정(사용할 거리 함수, 밀도 임계값 또는 예상 클러스터 수와 같은 파라미터 포함)은 개별 데이터 세트 및 결과의 의도된 용도에 따라 달라집니다.클러스터 분석은 자동 작업이 아니라 시행과 실패를 수반하는 지식 발견 또는 대화형 다목적 최적화의 반복 프로세스입니다.결과가 원하는 속성을 얻을 때까지 데이터 전처리 및 모델 파라미터를 수정해야 하는 경우가 많습니다.

군집화라는 용어 외에도 자동분류, 수치분류, 식물학(그리스어 βββδδδδα "grape"에서 유래), 유형학적 분석, 군집탐지 등 유사한 의미를 가진 용어들이 많이 있다.미묘한 차이는 종종 결과의 사용에 있다. 데이터 마이닝에서는 결과 그룹이 관심사이며, 자동 분류에서는 결과적인 차별력이 관심사이다.

클러스터 분석은 1932년^[1] Driver와 Krober에 의해 인류학에서 시작되었고^[2] 1938년 Joseph Zubin과 1939년^[3] Robert Tryon에 의해 심리학에 도입되었고 1943년부터^[4] Cattell에 의해 성격 심리학 특성 이론 분류에 사용된 것으로 유명하다.

정의.

「클러스터」의 개념은 정확하게 정의할 수 없기 때문에, 클러스터링 알고리즘이 ^[5]많은 이유 중 하나입니다.데이터 객체 그룹이라는 공통 분모가 있습니다.그러나 서로 다른 연구자가 서로 다른 클러스터 모델을 사용하며, 이러한 클러스터 모델 각각에 대해 서로 다른 알고리즘을 제공할 수 있습니다.클러스터의 개념은 알고리즘에 따라 특성이 크게 다릅니다.이러한 「클러스터 모델」을 이해하는 것은, 다양한 알고리즘의 차이를 이해하는 열쇠입니다.일반적인 클러스터 모델은 다음과 같습니다.

• 연결 모델: 예를 들어 계층형 클러스터링은 거리 연결을 기반으로 모델을 구축합니다.
• 중심 모형: 예를 들어, k-평균 알고리즘은 각 군집을 단일 평균 벡터로 나타냅니다.
• 분포 모형: 기대 최대화 알고리즘에서 사용되는 다변량 정규 분포와 같은 통계 분포를 사용하여 군집을 모형화합니다.
• 밀도 모델(예: DBSCAN 및 Optics)은 데이터 공간에서 클러스터를 연결된 밀도 영역으로 정의합니다.
• 서브스페이스 모델: 바이클러스터링(공동클러스터링 또는 2-모드클러스터링이라고도 함)에서는 클러스터 멤버와 관련 속성을 모두 사용하여 클러스터를 모델링합니다.
• 그룹 모델: 일부 알고리즘은 결과에 대한 정교한 모델을 제공하지 않고 그룹 정보만 제공합니다.
• 그래프 기반 모델: 그룹, 즉 하위 집합의 각 두 노드가 가장자리에 의해 연결되도록 그래프에서 노드의 하위 집합으로 간주할 수 있습니다.완전한 접속 요건의 완화(에지의 일부가 누락될 수 있음)는 HCS 클러스터링 알고리즘과 같이 준클릭이라고 불립니다.
• 부호 있는 그래프 모델: 부호 있는 그래프의 모든 경로에는 가장자리에 있는 기호의 곱에서 온 기호가 있습니다.균형 이론의 가정 하에서 모서리는 부호를 바꾸고 분기 그래프를 만들 수 있습니다.더 약한 "클러스터빌리티 공리"(정확히 음의 가장자리가 하나만 있는 사이클은 없음)는 세 개 이상의 클러스터 또는 양의 ^[6]가장자리만 있는 하위 그래프로 결과를 산출합니다.
• 뉴럴 모델: 가장 잘 알려진 비감독 뉴럴 네트워크는 자기조직화 맵이며, 이러한 모델은 보통 위의 모델 중 하나 이상과 유사하며, 뉴럴 네트워크가 주성분 분석 또는 독립성분 분석의 형태를 구현할 때 하위 공간 모델을 포함하는 것으로 특징지을 수 있습니다.

"클러스터링"은 기본적으로 이러한 클러스터 집합이며, 일반적으로 데이터 집합의 모든 개체를 포함합니다.또한 클러스터 간의 관계를 지정할 수 있습니다(예: 서로 내장된 클러스터 계층).클러스터화는 대략 다음과 같이 구분할 수 있습니다.

• 하드 클러스터링: 각 개체가 클러스터에 속하는지 여부
• 소프트 클러스터링(퍼지 클러스터링): 각 오브젝트는 어느 정도 각 클러스터에 속합니다(클러스터에 속할 가능성 등).

다음과 같은 미세한 차이도 있습니다.

• 엄격한 파티셔닝 클러스터링: 각 개체는 정확히 하나의 클러스터에 속합니다.
• 특이치를 사용한 엄격한 분할 클러스터링: 개체도 클러스터에 속하지 않을 수 있으며 특이치로 간주됩니다.
• 중복 클러스터링(또한 대체 클러스터링, 멀티 뷰 클러스터링): 오브젝트는 여러 클러스터에 속할 수 있습니다.일반적으로 하드 클러스터가 포함됩니다.
• 계층 클러스터링: 하위 클러스터에 속하는 개체도 상위 클러스터에 속합니다.
• 서브스페이스 클러스터링: 중복되는 클러스터링은 고유하게 정의된 서브스페이스 내에서 중복되지 않을 것으로 예상됩니다.

알고리즘

위와 같이 클러스터링 알고리즘은 클러스터 모델에 따라 분류할 수 있습니다.다음 개요에서는 클러스터링 알고리즘의 가장 중요한 예만을 보여 줍니다.이는 퍼블리싱된 클러스터링 알고리즘이 100개를 넘을 가능성이 있기 때문입니다.모두 군집에 대한 모형을 제공하는 것은 아니므로 쉽게 분류할 수 없습니다.위키피디아에서 설명된 알고리즘의 개요는 통계 알고리즘 목록에서 찾을 수 있다.

객관적으로 "올바른" 클러스터링 알고리즘은 없지만, 이미 언급했듯이 "^[5]클러스터링은 보는 사람의 눈에 달려 있습니다."특정 문제에 가장 적합한 클러스터링 알고리즘은 어떤 클러스터 모델을 다른 클러스터 모델보다 선호하는 수학적 이유가 없는 한 종종 실험적으로 선택해야 합니다.한 종류의 모델을 위해 설계된 알고리즘은 일반적으로 근본적으로 다른 종류의 ^[5]모델을 포함하는 데이터 세트에서 실패합니다.예를 들어, k-평균은 볼록하지 않은 ^[5]군집을 찾을 수 없습니다.

접속 기반 클러스터링(계층형 클러스터링)

계층형 클러스터링이라고도 하는 연결 기반 클러스터링은 객체가 멀리 있는 객체보다 가까운 객체와 더 관련이 있다는 핵심 개념을 기반으로 합니다.이러한 알고리즘은 "객체"를 연결하여 거리에 따라 "클러스터"를 형성합니다.클러스터는 주로 클러스터의 일부를 연결하는 데 필요한 최대 거리로 설명할 수 있습니다.서로 다른 거리에서는 서로 다른 클러스터가 형성되며, 덴드로그램(dendrogram)을 사용하여 나타낼 수 있습니다. 덴드로그램은 "계층형 클러스터링"이라는 공통 이름의 유래를 설명합니다. 이러한 알고리즘은 데이터 세트의 단일 분할을 제공하는 것이 아니라 특정 거리에서 서로 병합되는 광범위한 클러스터 계층을 제공합니다.덴드로그램에서 Y축은 클러스터가 병합되는 거리를 표시하고 개체는 클러스터가 혼합되지 않도록 X축을 따라 배치됩니다.

연결 기반 클러스터링은 거리 계산 방식에 따라 다른 전체 메서드 패밀리입니다.거리 함수의 일반적인 선택과는 별도로, 사용자는 사용할 연결 기준(클러스터가 여러 개체로 구성되므로 거리를 계산할 여러 후보가 있음)도 결정해야 합니다.일반적인 선택지는 단일 링크 클러스터링(객체 거리의 최소), 완전한 링크 클러스터링(객체 거리의 최대), UPGMA 또는 WPGMA(평균 링크 클러스터링이라고도 함)입니다.게다가 계층형 클러스터링은, 집약형(단일 요소로부터 시작해 클러스터로 집약) 또는 분할형(전체 데이터 세트로부터 시작해 파티션으로 분할)으로 할 수 있습니다.

이러한 방법을 사용하면 데이터 세트의 고유한 파티셔닝이 아니라 사용자가 적절한 클러스터를 선택해야 하는 계층이 생성됩니다.이들은 특이치에 대해 매우 강력하지 않으며, 이는 추가 클러스터로 나타나거나 다른 클러스터(특히 단일 링크 클러스터링의 경우 "체인 현상"으로 알려져 있음)를 발생시킵니다.일반적인 경우, 복잡도는${\displaystyle }$O(${\displaystyle {n\mathrm{}}^{}}$ 3$)($응집 클러스터링의 경우 {$displaystyle {O}(n^{3})$이고,^[7] 분할 클러스터링의${\displaystyle {경우}^{}}$O($)$ {$displaystyle {O}(2^{n-1})$로, $대규모{\displaystyle \mathcal{}}$ 데이터 세트에는 너무 느립니다.일부 특수한 경우($복잡도{\displaystyle \mathcal{}}$O ( ${\displaystyle {n\mathrm{}}^{}}$)$${$displaystyle {mathcal {O}}(n^{2$의 최적의 효율적인 방법이 알려져 있습니다. 단일^[8] 링크의 경우 SLINK, 완전한^[9] 링크 클러스터링을 위한 CLINK입니다.

• 링크 군집화
• 

  가우스 데이터에 대한 단일 링크.35개의 클러스터에서는 가장 큰 클러스터가 작은 부분으로 분할되기 시작하지만 단일 링크 효과로 인해 두 번째로 큰 클러스터가 여전히 연결됩니다.

• 

  밀도 기반 클러스터 상의 단일 링크. 링크 클러스터링에는 "노이즈" 개념이 없기 때문에 대부분 단일 요소를 포함하는 20개의 클러스터가 추출됩니다.

중심 기반 클러스터링

중심 기반 군집 분석에서 각 군집은 데이터 집합의 구성원이 아닌 중심 벡터로 표시됩니다.군집 수가 k로 고정된 경우 k-평균 군집 분석은 최적화 문제로 공식적인 정의를 제공합니다. 즉, 군집으로부터의 거리 제곱이 최소화되도록 k 군집 중심을 찾고 개체를 가장 가까운 군집 중심에 할당합니다.

최적화 문제 자체는 NP-hard로 알려져 있기 때문에 일반적인 접근방식은 대략적인 솔루션만을 검색하는 것입니다.특히 잘 알려진 대략적인 방법은 로이드 ^[10]알고리즘으로, 종종 "k-평균 알고리즘"이라고 불린다(다른 알고리즘이 이 이름을 도입하긴 했지만).그러나 로컬 최적값만 찾으며 일반적으로 서로 다른 랜덤 초기화로 여러 번 실행됩니다.k-평균의 변동에는 종종 다중 런의 최적화를 선택할 뿐 아니라 중심점을 데이터 집합의 멤버로 제한(k-중위수 군집 분석), 중위수 선택(k-중위수 군집 분석), 초기 중심을 덜 랜덤하게 선택(k-평균+)하거나 애매한 군집 할당을 허용(퍼지 c-평균)하는 등의 최적화가 포함됩니다.

대부분의 k-평균형 알고리즘에서는 클러스터 수 k를 미리 지정해야 하며, 이는 이러한 알고리즘의 가장 큰 결점 중 하나로 간주됩니다.또한 알고리즘은 항상 가장 가까운 중심에 개체를 할당하기 때문에 크기가 거의 비슷한 클러스터를 선호합니다.이로 인해 클러스터 경계선이 잘못 절단되는 경우가 많습니다(알고리즘에 의해 클러스터 경계선이 아닌 클러스터 중심이 최적화되므로 놀랄 일도 아닙니다).

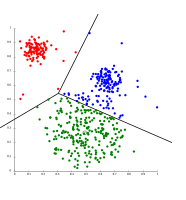
K-평균은 여러 가지 흥미로운 이론적 성질을 가지고 있다.먼저 데이터 공간을 Voronoi 다이어그램으로 알려진 구조로 분할합니다.둘째, 개념적으로 가장 가까운 이웃 분류에 가깝기 때문에 기계 학습에서 인기가 있다.셋째, 모델 기반 클러스터링의 변형으로 볼 수 있으며, Lloyd의 알고리즘은 아래에서 설명한 이 모델의 기대 최대화 알고리즘의 변형으로 볼 수 있습니다.

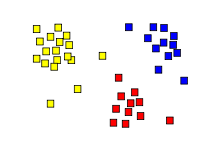
• k-표준 군집 분석 예제
• 

  k-평균은 동일한 크기의 클러스터를 가정하는 Voronoi 셀로 데이터를 분리한다(여기서는 적절하지 않음).

• 

  k-module은 밀도 기반 클러스터를 나타낼 수 없습니다.

k-평균 및 k-중간체와 같은 중심 기반 클러스터링 문제는 운영 연구 및 계산 기하학 커뮤니티의 표준 문제인 캡슐화되지 않은 미터법 시설 위치 문제의 특별한 경우이다.기본적인 시설 위치 문제(더 정교한 설정을 모델링하는 수많은 변종들이 있음)에서는 주어진 일련의 소비자에게 최적의 서비스를 제공할 수 있는 최적의 창고 위치를 찾는 것이 과제입니다.「웨어하우스」는 클러스터 중심, 「컨슈머 로케이션」은 클러스터화할 데이터로 간주할 수 있습니다.이를 통해 시설 위치 문헌에서 잘 개발된 알고리즘 솔루션을 현재 고려되고 있는 중심 기반 클러스터링 문제에 적용할 수 있다.

분산 기반 클러스터링

통계량과 가장 밀접한 관련이 있는 군집화 모형은 분포 모형을 기반으로 합니다.클러스터는 동일한 분포에 가장 많이 속하는 개체로 쉽게 정의할 수 있습니다.이 접근법의 편리한 속성은 이것이 분포에서 랜덤 객체를 추출함으로써 인공 데이터 세트가 생성되는 방식과 매우 유사하다는 것이다.

이러한 방법의 이론적 기초는 훌륭하지만, 모델의 복잡성에 제약이 가해지지 않는 한, 과적합이라고 하는 중요한 문제가 있습니다.일반적으로 더 복잡한 모델은 데이터를 더 잘 설명할 수 있기 때문에 적절한 모델 복잡성을 선택하는 것이 본질적으로 어렵습니다.

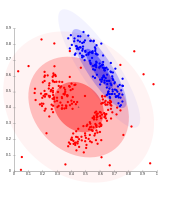
대표적인 방법은 가우스 혼합 모델(기대-최대화 알고리즘 사용)로 알려져 있습니다.여기서 데이터 세트는 일반적으로 랜덤으로 초기화되고 파라미터가 데이터 세트에 더 잘 적합하도록 반복적으로 최적화되는 고정된 수의 가우스 분포로 모델링됩니다.이 값은 로컬 최적값으로 수렴되므로 런을 여러 번 실행하면 서로 다른 결과가 나올 수 있습니다.하드 클러스터링을 취득하기 위해 오브젝트는 대부분의 경우 그들이 속할 가능성이 가장 높은 가우스 분포에 할당됩니다.소프트 클러스터에서는 이것이 필요하지 않습니다.

분산 기반 클러스터링은 속성 간의 상관 관계와 종속성을 캡처할 수 있는 복잡한 클러스터 모델을 생성합니다.그러나 이러한 알고리즘은 사용자에게 추가적인 부담을 준다. 즉, 많은 실제 데이터 세트의 경우, 간결하게 정의된 수학적 모델이 없을 수 있다(예: 데이터에 대한 가우스 분포가 다소 강력한 가정이라고 가정).

• 가우스 혼합물 모델 클러스터링 예제
• 

  가우스 분포 데이터에서는 클러스터 모델링에 가우시안(Gaussian)을 사용하기 때문에 잘 작동한다.

• 

  밀도 기반 클러스터는 가우스 분포를 사용하여 모델링할 수 없습니다.

밀도 기반 클러스터링

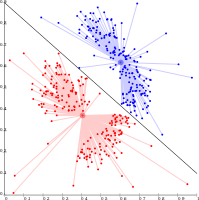
밀도 기반 ^[11]클러스터링에서 클러스터는 데이터 세트의 나머지 영역보다 밀도가 높은 영역으로 정의됩니다.클러스터를 분리하기 위해 필요한 희박한 영역의 개체는 일반적으로 노이즈와 경계점으로 간주됩니다.

가장 일반적인^[12] 밀도 기반 클러스터링 방법은 DBSCAN입니다.^[13]새로운 많은 방법과는 달리, "밀도 도달 가능성"이라고 불리는 잘 정의된 클러스터 모델을 특징으로 합니다.링크 기반 클러스터링과 마찬가지로 특정 거리 임계값 내의 연결 지점을 기반으로 합니다.그러나 이 반지름 내의 최소 다른 개체 수로 정의된 원래 변형에서 밀도 기준을 충족하는 점만 연결합니다.클러스터는 모든 밀도 연결 개체(다른 많은 메서드와 달리 임의 모양의 클러스터를 형성할 수 있음)와 이러한 개체의 범위 내에 있는 모든 개체로 구성됩니다.DBSCAN의 또 다른 흥미로운 특성은 복잡성이 상당히 낮다는 것입니다. 즉, 데이터베이스에 선형적인 수의 범위 쿼리가 필요하며 각 실행에서 기본적으로 동일한 결과(핵심 및 노이즈 포인트에 대해서는 결정적이지만 경계 포인트에 대해서는 결정적이지 않음)를 발견하기 때문에 여러 번 실행할 필요가 없습니다.Optics는^[14] DBSCAN의 일반화로 범위 파라미터 $"\display\varepsilon$에 적절한 값을 선택할 필요가 없어지며 링크 클러스터링과 관련된 계층적 결과를 생성합니다.DeLi-Clu,^[15] Density-Link-Clustering은 $단일{\displaystyle }$ 링크 클러스터링과 Optics의 아이디어를 결합하여 $§\displaystyle\varepsilon$ 파라미터를$$ 완전히 삭제하고 R-tree 인덱스를 사용하여 Optics보다 성능을 향상시킵니다.

DBSCAN 및 Optics의 주요 단점은 클러스터 경계를 감지하기 위한 밀도 저하가 예상된다는 것입니다.예를 들어 가우스 분포가 겹치는 데이터 세트(인공 데이터의 일반적인 사용 사례)에서는 클러스터 밀도가 지속적으로 감소하기 때문에 이러한 알고리즘에 의해 생성되는 클러스터 경계는 종종 임의적으로 보입니다.가우시안 혼합으로 구성된 데이터 집합에서 이러한 알고리즘은 거의 항상 이러한 종류의 데이터를 정밀하게 모델링할 수 있는 EM 클러스터링과 같은 방법에 의해 성능이 향상된다.

평균 이동은 커널 밀도 추정에 기반하여 각 개체를 근처의 가장 밀도가 높은 영역으로 이동하는 클러스터링 방법입니다.결국, 물체는 국소 밀도의 극대치로 모인다.k-평균 군집 분석과 마찬가지로 이러한 "밀도 유인기"는 데이터 집합을 대표하는 역할을 할 수 있지만, 평균 이동은 DBSCAN과 유사한 임의 모양의 클러스터를 탐지할 수 있습니다.비용이 많이 드는 반복 절차와 밀도 추정 때문에 평균 이동은 일반적으로 DBSCAN 또는 k-평균보다 느립니다.게다가 다차원 데이터에 대한 평균 시프트 알고리즘의 적용 가능성은,^[15] 클러스터 테일의 과잉 프래그먼테이션을 초래하는 커널 밀도 추정의 매끄러운 동작에 의해서 방해된다.

• 밀도 기반 클러스터링 예시
• 

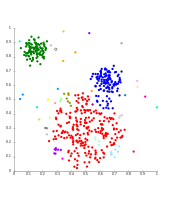
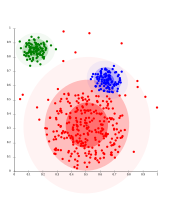
  DBSCAN을 통한 밀도 기반 클러스터링

• 

  DBSCAN은 같은 밀도의 클러스터를 상정하고 있으며, 인근 클러스터를 분리하는 데 문제가 있을 수 있습니다.

• 

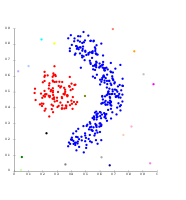
  Optics는 DBSCAN의 변종이며, 다양한 밀도의 클러스터의 처리 능력을 향상시킵니다.

그리드 기반 클러스터링

그리드 기반 기술은 다차원 데이터 ^[16]세트에 사용됩니다.이 기술에서는 그리드 구조를 만들고 그리드(셀이라고도 함)에서 비교가 수행됩니다.그리드 기반 기술은 빠르고 계산 복잡도가 낮습니다.그리드 기반 클러스터링 방법에는 STING과 CLIQUE의 두 가지 유형이 있습니다.그리드 기반 클러스터링 알고리즘과 관련된 단계는 다음과 같습니다.

1. 데이터 공간을 한정된 수의 셀로 분할합니다.
2. 셀 'c'를 랜덤으로 선택합니다.여기서 c는 사전에 횡단하지 마십시오.
3. 'c'의 밀도를 계산합니다.
4. 'c' 밀도가 임계값 밀도보다 큰 경우
   1. 셀 'c'를 새 클러스터로 표시
   2. 'c'의 모든 인접 밀도를 계산합니다.
   3. 네이버 셀의 밀도가 임계값 밀도보다 클 경우 클러스터에 셀을 추가하고 임계값 밀도보다 밀도가 큰 네이버가 없을 때까지 스텝 4.2와 4.3을 반복합니다.
5. 모든 셀이 통과할 때까지 스텝 2, 3, 4를 반복합니다.
6. 이제 그만.

최근의 동향

최근 몇 년 동안 ^[17][18]기존 알고리즘의 성능을 개선하기 위해 상당한 노력을 기울였다.CLARANS와 ^[19]BIRCH가 ^[20]그 중 하나입니다.최근에는 대규모 데이터 세트(빅 데이터라고도 함)를 처리할 필요가 있어 퍼포먼스를 위해 생성된 클러스터의 의미적 의미를 교환할 의향이 높아지고 있습니다.이로 인해 캐노피 클러스터링과 같은 사전 클러스터화 방법이 개발되었지만, 그 결과 발생하는 "클러스터"는 데이터 세트의 대략적인 사전 파티션화일 뿐이며, k-평균 클러스터링과 같은 기존의 느린 방법으로 파티션을 분석합니다.

고차원 데이터의 경우, 많은 기존 방법이 차원성의 저주로 인해 실패하며, 이로 인해 고차원 공간에서 특정 거리 함수가 문제가 된다.그 결과 서브스페이스 클러스터링(일부 속성만 사용되며 클러스터 모델에는 클러스터의 관련 속성이 포함됨)에 초점을 맞춘 고차원 데이터에 대한 새로운 클러스터링 알고리즘과 상관관계를 제공함으로써 모델링할 수 있는 임의의 회전("상관된") 서브스페이스 클러스터를 찾는 상관관계 클러스터링도 도입되었습니다.그들의 속성.^[21]이러한 클러스터링 알고리즘의 예로는 CLIQU 및 SUBBU가 ^[23]있습니다^[22].

density-based 말씀 드렸다시피 방법(특히 DBSCAN/OPTICS 가족의 알고리즘)에서 아이디어 subspace 클러스터링(HiSC,[24]계층적 부분 공간까지 군집 화가 되고 DiSH[25])과 상관 관계(HiCO,[26]계층적 상관 군집화, 4C[27]"상관 연결"과 ERiC[28]을 사용하여 클러스터링도록 계층적 D를 탐험하면서 각색되었다correlaensity-based클러스터).

상호 정보를 기반으로 하는 몇 가지 다른 클러스터링 시스템이 제안되었습니다.하나는 Marina Meilher의 정보 ^[29]메트릭의 변화이며, 다른 하나는 계층적 ^[30]클러스터링을 제공합니다.유전자 알고리즘을 사용하여 상호 ^[31]정보를 포함하여 다양한 적합성 기능을 최적화할 수 있다.또한 컴퓨터 과학과 통계 물리학에서 최근 발전된 믿음 전파는 새로운 유형의 클러스터링 알고리즘의 ^[32]창조로 이어졌다.

평가 및 평가

클러스터링 결과의 평가(또는 "검증")는 클러스터링 ^[33]자체만큼 어렵습니다.일반적인 접근법에는 클러스터링을 단일 품질 점수로 요약하는 "내부" 평가, 클러스터링을 기존 "근거 진실" 분류와 비교하는 "외부" 평가, 인간 전문가의 "수동" 평가 및 의도된 애플리케이션에서의 클러스터링의 효용성을 평가하여 "간접" 평가가 포함됩니다.n.^[34]

내부평가척도는 그 자체가 클러스터링 대상으로 볼 수 있는 기능을 나타낸다는 문제로 어려움을 겪고 있다.예를 들어, 실루엣 계수로 데이터 세트를 클러스터링할 수 있지만, 이를 위한 알려진 효율적인 알고리즘은 없습니다.이러한 내부측정을 평가에 사용함으로써 ^[34]최적화 문제의 유사성을 비교하고 클러스터링이 얼마나 유용한지는 비교하지 않는다.

외부 평가에도 유사한 문제가 있습니다. 이러한 "실질적" 라벨이 있으면 클러스터화할 필요가 없습니다.실제 적용에서는 보통 이러한 라벨이 없습니다.한편, 라벨은 데이터 세트의 가능한 분할을 1개만 반영합니다.이것은 다른 클러스터링이 존재하지 않는 것을 의미하지는 않습니다.

따라서 이러한 접근법 중 어느 것도 궁극적으로 클러스터화의 실제 품질을 판단할 수는 없지만,^[34] 이는 매우 주관적인 인간의 평가가 필요합니다.그럼에도 불구하고, 그러한 통계는 나쁜 ^[35]집단을 식별하는 데 매우 유익할 수 있지만, 주관적인 인간 ^[35]평가를 무시해서는 안 된다.

내부평가

클러스터링된 데이터 자체를 기반으로 클러스터링 결과를 평가하는 경우 이를 내부 평가라고 합니다.이러한 방법은 일반적으로 클러스터 내에서 유사성이 높고 클러스터 간 유사성이 낮은 클러스터를 생성하는 알고리즘에 최고의 점수를 할당합니다.클러스터 평가에서 내부 기준을 사용하는 것의 한 가지 단점은 내부 측정 점수가 높다고 해서 반드시 효과적인 정보 검색 애플리케이션이 ^[36]되는 것은 아니라는 것입니다.또한 이 평가는 동일한 클러스터 모델을 사용하는 알고리즘에 치우쳐 있습니다.예를 들어, k-평균 군집화는 자연스럽게 객체 거리를 최적화하며 거리 기반 내부 기준은 결과 군집화를 과대평가할 가능성이 높다.

따라서 내부 평가 척도는 한 알고리즘이 다른 알고리즘보다 더 나은 성능을 발휘하는 상황에 대한 통찰력을 얻는 데 가장 적합하지만, 이것이 한 알고리즘이 다른 ^[5]알고리즘보다 더 유효한 결과를 산출한다는 것을 의미하지는 않는다.이러한 지수에 의해 측정되는 유효성은 데이터 집합에 이러한 구조가 존재한다는 주장에 따라 달라집니다.데이터 세트에 근본적으로 다른 모델 세트가 포함되어 있거나 평가가 근본적으로 다른 ^[5]기준을 측정하는 경우, 어떤 종류의 모델에 대해 설계된 알고리즘은 가능성이 없습니다.예를 들어, k-평균 군집 분석에서는 볼록 군집만 찾을 수 있으며 많은 평가 지수는 볼록 군집을 가정합니다.비볼록 클러스터가 있는 데이터 집합에서는 k-평균의 사용이나 볼록성을 가정하는 평가 기준의 사용이 타당하지 않다.

일반적으로 동일한 군집의 항목이 서로 다른 ^{[37]: 115–121} 군집의 항목보다 더 유사해야 한다는 직관에 따라 12개 이상의 내부 평가 척도가 존재합니다.예를 들어 다음 방법을 사용하여 내부 기준에 따라 클러스터링 알고리즘의 품질을 평가할 수 있습니다.

• 데이비스-볼딘 지수

데이비스-볼딘 지수는 다음 공식으로 계산할 수 있다.

${\displaystyle DB=black {1}{n}\sum _{i=1}^{n}\max _{j\neq i}\leftflac {j}{d(c_{i}+\flac _{j}}}{d(c_i},c_{j}}}}}}\right}$

여기서 n은 클러스터 수, $c{\displaystyle {}_{}}$ {\$displaystyle c_$${i$$}$는 $클러스터{\displaystyle }$i {\$displaystyle$$$i$\}$의 중심, ${\displaystyle i_{}}$i {$$$displaystyle i$는 $클러스터{\displaystyle {}_{}}$$$${\displaystyle i_{}}$의 모든 요소의 중심 및 $d{\displaystyle ({}_{}{}_{}}$ j$)$에 대한 평균 거리입니다.$e$ d$(c_{i}, c_{j})$는 $centroids{\displaystyle {}_{}}$ ${\displaystyle {ci}_{}}${{$displaystyle c_{i$}}와 ${\displaystyle c_{}}${\$displaystyle c_{$j$\}\}$ 사이의 거리입니다.클러스터 내 거리(클러스터 내 유사성이 높음)와 클러스터 간 거리(클러스터 간 유사성이 낮음)를 갖는 알고리즘은 클러스터,가장 작은 Davies-Bouldin 지수를 가진 클러스터의 컬렉션을 생성하는 에링 알고리즘은 이 기준에 따라 최적의 알고리즘으로 간주됩니다.

• 던 지수

Dunn 지수는 밀도가 높고 잘 분리된 클러스터를 식별하는 것을 목표로 합니다.이는 최소 클러스터 간 거리와 최대 클러스터 간 거리 간의 비율로 정의됩니다.각 클러스터 파티션에 대해 Dunn 인덱스는 다음 ^[38]공식으로 계산할 수 있습니다.

${\displaystyle D=param frac {1\leq i<j\leq n}d(i,j)}{\max _1\leq k\leq n}d^{\prime }(k)},},}$

여기서 d(i,j)는 군집 i와 j 사이의 거리를 나타내고 d '(k)'는 군집 k의 군집 내 거리를 측정합니다.두 군집 사이의 군집 간 거리 d(i,j)는 군집의 중심 간 거리 등 임의의 수의 거리 측도가 될 수 있습니다.마찬가지로, 클러스터 내 거리 d '(k)'는 클러스터 k 내의 모든 요소 쌍 사이의 최대 거리 등 다양한 방법으로 측정될 수 있다.내부 기준은 클러스터 내 유사성이 높고 클러스터 간 유사성이 낮은 클러스터를 추구하기 때문에 Dunn 인덱스가 높은 클러스터를 생성하는 알고리즘이 더 바람직합니다.

• 실루엣 계수

실루엣 계수는 동일한 군집의 요소까지의 평균 거리와 다른 군집의 요소까지의 평균 거리를 비교합니다.실루엣 값이 높은 객체는 잘 클러스터된 것으로 간주되며 값이 낮은 객체는 특이치일 수 있습니다.이 지수는 k-평균 ^{[citation needed]}군집 분석과 잘 작동하며 최적의 군집 수를 결정하는 데도 사용됩니다.

외부평가

외부 평가에서 클러스터링 결과는 알려진 클래스 레이블 및 외부 벤치마크와 같이 클러스터링에 사용되지 않은 데이터를 기반으로 평가됩니다.이러한 벤치마크는 사전 분류된 항목 집합으로 구성되며, 이러한 집합은 종종 (전문가가) 인간에 의해 작성된다.따라서 벤치마크 세트는 평가를 ^[33]위한 골드 스탠다드로 간주할 수 있습니다.이러한 유형의 평가 방법은 클러스터링이 미리 결정된 벤치마크 클래스에 얼마나 가까운지를 측정합니다.그러나 클래스는 내부 구조를 포함할 수 있기 때문에 클래스는 클러스터 분리를 허용하지 않거나 클래스가 ^[39]이상을 포함할 수 있기 때문에 이것이 실제 데이터에 적합한지 또는 사실에 근거한 사실을 가진 합성 데이터 세트에만 적합한지에 대해 최근 논의되었다.또, 지식 발견의 관점에서는, 기존의 지식의 재현이 반드시 의도한 ^[39]결과는 아닐 수도 있습니다.clustering 프로세스에서 이미 메타데이터 정보(클래스 라벨 등)가 사용되고 있는 제약이 있는 clustering의 특수한 시나리오에서는 평가 목적의 정보의 홀드아웃은 ^[40]간단하지 않습니다.

분류 작업을 평가하는 데 사용되는 변형에서 많은 측정이 수정된다.이러한 페어 카운트 메트릭은 클래스가 단일 데이터 포인트에 올바르게 할당된 횟수(진정한 긍정)를 ^[33]카운트하는 대신 실제로 동일한 클러스터에 있는 각 데이터 포인트 쌍이 예측되는지 여부를 평가합니다.

내부 평가와 마찬가지로 다음과 같은 몇 가지 외부 평가 척도가 존재합니다.^{[37]: 125–129}

• 순도: 순도는 군집이 단일 ^[36]클래스를 포함하는 정도를 나타내는 척도입니다.이 계산은 다음과 같이 생각할 수 있습니다.각 클러스터에 대해 해당 클러스터에서 가장 일반적인 클래스의 데이터 지점 수를 세십시오.이제 모든 군집의 합계를 총 데이터 점 수로 나눕니다.공식적으로 클러스터 $(\displaystyle$ M$)$ 및$$ $클래스{\displaystyle }$ D$(\displaystyle$ D$)$의 일부 세트가 N$(\displaystyle$ N$)$ 데이터$$ 포인트를 $분할$하는 경우 순도는 다음과 같이 정의할 수 있습니다.

${\displaystyle {1}{N}\sum _{m\in M}\max _{d\in D}{m\cap d}}$

이 척도는 클러스터 수가 많다고 해서 불이익을 주는 것은 아니며 클러스터 수가 많을수록 순도가 높아집니다.순도 점수 1은 각 데이터 점을 자체 클러스터에 배치함으로써 항상 가능합니다.또한 성능이 낮은 클러스터링 알고리즘에서도 높은 순도 값을 제공하는 불균형 데이터에는 순도가 잘 작동하지 않습니다.예를 들어 크기 1000의 데이터 세트가 999개의 포인트를 포함하는 클래스와 1개의 포인트를 포함하는 클래스로 구성되어 있는 경우 가능한 모든 파티션의 순도는 99.9% 이상입니다.

• 랜드 인덱스^[41]

랜드 지수는 군집 분석 알고리즘에 의해 반환된 군집이 벤치마크 분류와 얼마나 유사한지를 계산합니다.다음 공식을 사용하여 계산할 수 있습니다.

${\displaystyle RI=black {TP+}TN}{TP+FP+FN+TN}}}$

${\displaystyle \mathrm{여기}}$서 T P$(\displaystyle$ TP$)$는 참 음수, $TN{\displaystyle }$$(\displaystyle TN)$은 참 음수, $(\displaystyle$ FP$)$는 거짓 음수, $(\displaystyle$ FN)은$$거짓$$ 음수입니다.여기서 카운트되는 인스턴스는 올바른 쌍별 할당 수입니다.즉, T $(\displaystyle$TP)는 예측된 파티션에서 함께 군집된 점 쌍의 수이며, F $(\displaystyle$ FP$)$는 예측된 파티션에서 군집된 점 쌍의 수이며, 접지된 점 파티션 등에서 군집되지 않은 점 쌍의 수입니다.데이터 세트가 N 크기이면 ${\displaystyle T}$P + ${\displaystyle T}$N + ${\displaystyle F}$P + ${\displaystyle F}$ N ${\displaystyle =}$ ( ${\displaystyle N\genfrac{}{}{0ex}{}{}{}}$ ${\displaystyle \genfrac{}{}{0ex}{}{2}{}}$ $)(\$ TP$+)$$TN+FP+FN=binom {N}{2$

랜드 지수의 한 가지 문제는 거짓 긍정과 거짓 부정의 가중치가 동일하다는 것이다.이는 일부 클러스터링 애플리케이션에서는 바람직하지 않은 특성일 수 있습니다.F-measure는 이 ^{[citation needed]}문제를 해결하며, 기회 보정된 랜드 지수 또한 해결합니다.

• F-measure

F-measure는 $파라미터{\displaystyle }$ ${\$ 0(\style$\display\beta\geq$ 0$)$을 통해 호출의 가중치를 부여함으로써 잘못된 음의 기여 균형을 맞출 수 있다. 정밀도 및 호출(외부 평가 척도 자체)은 다음과 같이 정의한다.

${\displaystyle P=param frac {TP}{TP+FP}}}$

${\displaystyle R=param frac {TP}{TP+FN}}}$

$여기$서$$P(\$displaystyle$ P$)$는 정밀도 비율이고 R$(\displaystyle$ R$)$은 회수율입니다.F 측정은 다음 ^[36]공식을 사용하여 계산할 수 있습니다.

${\displaystyle F_{\beta }= flac {(\display ^{2}+1)\cdot P\cdot R}{\beta ^{2}\cdot P+R}}}$

${\displaystyle \mathrm{\beta }}$ ${\displaystyle =}$0 {$displaystyle \displaystyle$ $=$$$0$}$일 때 $F{\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle P}$ ${\displaystyle$F_{0}=$P$ 즉, β ${\displaystyle =}$ ${\displaystyle 0}$ {$displaystyle \display$= 0$\}$일 $때{\displaystyle }$ 리콜은 F 측정에 영향을 주지 않으며, β$${$displaystyle \dicle }$이 증가하면 F-mature }이 호출에 가중치가 할당됩니다.

${\displaystyle \mathrm{또한}}$ TN$(디스플레이$ 스타일 TN$)$은 고려되지 않으며 0에서 0까지 바운드 없이 변경될 수 있습니다.

• 자카드 지수

Jaccard 지수는 두 데이터 세트 간의 유사성을 정량화하는 데 사용된다.Jaccard 인덱스는 0 ~1의 값을 취합니다.인덱스가 1이면 두 데이터 세트가 동일하고 인덱스가 0이면 데이터 세트에 공통 요소가 없음을 나타냅니다.Jaccard 지수는 다음 공식으로 정의됩니다.

${\displaystyle J(A,B)=subfrac {A\cap B}{A\cup B }}=subfrac {TP}{TP+FP+FN}}$

이는 단순히 두 세트에 공통되는 고유 요소의 수를 두 세트의 고유 요소의 총 수로 나눈 것입니다.

${\displaystyle \mathrm{또한}}$ TN$(디스플레이$ 스타일 TN$)$은 고려되지 않으며 0에서 0까지 바운드 없이 변경될 수 있습니다.

• 주사위 색인

Dice 대칭 측정은 $($ $스타일$ TN$)$을 무시한 채 $($$표시$ $스타일$ TP$)$의 무게를 두 배로 늘립니다.

${\displaystyle DSC=syslogfrac {2}TP}{2TP+FP+FN}}}$

• Fowlkes-Mallows 지수^[42]

Fowlkes-Mallows 지수는 클러스터링 알고리즘에 의해 반환된 클러스터와 벤치마크 분류 간의 유사성을 계산합니다.폴크스-몰로스 지수 값이 높을수록 군집과 벤치마크 분류가 더 유사하다.다음 공식을 사용하여 계산할 수 있습니다.

${\displaystyle FM=sqrt {\frac {TP}}{TP+FP}}\cdot {frac {TP}{TP+FN}}}}}}$

${\displaystyle \mathrm{여기}}$서 T P$(\displaystyle$ TP$)$는 참 긍정의 $,$ $FP$(\$displaystyle$FP$$)는 거짓 $긍정$의 $,$ $FN$(\$displaystyle$FN$$)은 거짓 부정의 수입니다.$FM($디스플레이 스타일 FM) 지수는 정밀도 및 $호출{\displaystyle }$ P$(디스플레이 스타일$ P$)$ 및$$ $(디스플레이 스타일$ R$)$의 기하 평균이며, 따라서 G 측정이라고도 하며, F 측정은 이들의 ^[43][44]조화 평균입니다.또한 정밀도와 리콜은 월러스 $지수{\displaystyle {}^{}}$ ${\displaystyle B^{}}$ I$(\$ B$^)$로도 알려져 있습니다.$I$$}}$ 및 $($ B$^{$$II$^[45] 회수, 정밀도 및 G-measure의 우연한 정규화 버전은 Informedness, Markeness 및 Matthews Correlation에 해당하며 Kappa와 ^[46]강하게 관련된다.

• 상호정보는 군집화와 두 군집 사이의 비선형 유사성을 검출할 수 있는 실측값 분류 간에 얼마나 많은 정보가 공유되는지에 대한 정보 이론적인 척도이다.정규화된 상호 정보는 다양한 클러스터 ^[33]번호에 대한 편중이 감소된 수정된 성능 변형 제품군입니다.
• 혼란 행렬

혼동 행렬을 사용하여 분류(또는 클러스터링) 알고리즘의 결과를 빠르게 시각화할 수 있습니다.클러스터가 골드 표준 클러스터와 얼마나 다른지 보여 줍니다.

클러스터 경향

클러스터 경향을 측정하는 것은 클러스터화할 데이터에 클러스터가 어느 정도 존재하는지 측정하는 것이며 클러스터화를 시도하기 전에 초기 테스트로 수행할 수 있습니다.이를 위한 한 가지 방법은 데이터를 랜덤 데이터와 비교하는 것입니다.평균적으로 랜덤 데이터에는 군집이 없어야 합니다.

• 홉킨스 통계

홉킨스 ^[47]통계에는 여러 가지 공식들이 있다.대표적인 것은 다음과 같습니다.^[48]X$(디스플레이 스타일$ X$)$를 d$(디스플레이 스타일$$$d$)$ 차원 공간에 있는$$$$$n개$의 데이터 포인트 $집합$으로 $합니다{\displaystyle }$.$멤버{\displaystyle {}_{}}$ ${\displaystyle {xi}_{}}$ ${\$의 데이터$$${\displaystyle }$포인트의 ${\displaystyle \mathrm{랜덤}}$ 샘플$($대체하지 않음)을 고려합니다.또한 랜덤하게 분포된 m ${\displaystyle$ m$}$의 $데이터{\displaystyle }$ 포인트 집합$$Y {\$displaystyle$ Y$}$를 생성합니다.다음으로 2개의 거리측정을 정의합니다$.$의 가장 가까운 이웃으로부터의 ${\displaystyle y_{}}$ ${\displaystyle y}$Y의 $거리{\displaystyle {}_{}}$($display$ style $y_{i}\in$ Y$)$와 $(\$ style $w_{i$})는$$ ${\displaystyle {xi}_{}x}$X의 가장 가까운 이웃으로부터의 $거리{\displaystyle {}_{}}$(\$displaystyle x_{i}\in$ X$)$입니다.그런 다음 홉킨스 통계를 다음과 같이 정의한다.

$({displaystyle H=hcfrac {i=1}^{m}{u_{i}^{d}}{\sum _{i}^{d}}+\sum _{i=1}^{m}{w_{i}^{d}}}},},$

이 정의를 사용하면 균일한 랜덤 데이터는 0.5에 가까운 값을 가지며 군집화된 데이터는 1에 가까운 값을 갖는 경향이 있습니다.

그러나, 단일 가우스만을 포함하는 데이터도 1에 가깝습니다. 이 통계는 멀티모달성이 아닌 균일한 분포에서 편차를 측정하기 때문에 이 통계는 응용 분야에서 거의 사용되지 않습니다(실제 데이터는 원격으로 균일하지 않기 때문입니다).

적용들

이 섹션은 확인을 위해 추가 인용문이 필요합니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.(2016년 11월) (이 템플릿메시지 삭제 방법 및 삭제 시기 확인)

생물학, 컴퓨터 생물학 및 생물정보학

식물 및 동물 생태학

클러스터 분석은 이기종 환경에서 유기체의 공동체(어셈블리)를 설명하고 공간 및 시간적으로 비교하기 위해 사용됩니다.또한 식물 계통학에서 여러 속성을 공유하는 종, 속 또는 그 이상의 수준에서 인공 계통학 또는 유기체(개체) 군집을 생성하기 위해 사용된다.

문자 변환학

군집화는 HCS ^[49][50]군집화 알고리즘에서와 같이 관련된 발현 패턴(공표현 유전자라고도 함)을 가진 유전자 그룹을 구축하는 데 사용됩니다.종종 그러한 그룹은 특정 경로의 효소나 공동 조절되는 유전자와 같은 기능적으로 관련된 단백질을 포함한다.표현 시퀀스 태그(EST) 또는 DNA 마이크로 어레이를 사용한 높은 스루풋 실험은 게놈 주석을 위한 강력한 도구가 될 수 있습니다.게노믹스의 일반적인 측면입니다.

시퀀스 분석

배열 클러스터링은 상동 배열을 유전자 ^[51]패밀리로 그룹화하기 위해 사용된다.이것은 생물정보학 및 진화생물학에서 일반적으로 매우 중요한 개념이다.유전자 복제로 진화를 보다.

높은 스루풋의 유전자형 입력 플랫폼

클러스터링 알고리즘은 유전자형을 ^[52]자동으로 할당하는 데 사용됩니다.

인간 유전자 클러스터링

유전자 데이터의 유사성은 집단 구조를 추론하기 위해 군집화에 사용된다.

약

의료 영상

PET 스캔에서는 클러스터 분석을 사용하여 3차원 영상에서 다양한 ^[53]유형의 조직을 여러 목적으로 구분할 수 있습니다.

항균활성 분석

클러스터 분석은 항생제 내성 패턴을 분석하고, 작용 메커니즘에 따라 항균 화합물을 분류하며, 항생제의 항균 활동에 따라 항생제를 분류하는 데 사용될 수 있다.

IMRT 세그멘테이션

클러스터링을 사용하여 MLC 기반 방사선 치료에서 결과 필드로 변환하기 위해 형광 지도를 개별 영역으로 분할할 수 있습니다.

비즈니스 및 마케팅

시장 조사

군집 분석은 조사 및 검정 패널의 다변량 데이터로 작업할 때 시장 조사에 널리 사용됩니다.시장 조사원은 클러스터 분석을 사용하여 일반 소비자를 시장 세그먼트로 분할하고 다양한 소비자 그룹/잠재 고객 간의 관계를 더 잘 이해하며, 시장 세분화, 제품 포지셔닝, 신제품 개발 및 테스트 시장 선택에 사용합니다.

쇼핑 아이템의 그룹화

클러스터링을 사용하면 웹에서 사용할 수 있는 모든 쇼핑 아이템을 고유한 제품 세트로 그룹화할 수 있습니다.예를 들어, eBay의 모든 아이템을 독특한 상품으로 분류할 수 있습니다(eBay는 SKU라는 개념이 없습니다).

월드 와이드 웹

소셜 네트워크 분석

소셜 네트워크 연구에서 클러스터링은 대규모 그룹 내 커뮤니티를 인식하기 위해 사용될 수 있다.

검색 결과 그룹화

파일과 웹사이트를 지능적으로 그룹화하는 과정에서 클러스터링은 구글과 같은 일반^{[citation needed]} 검색 엔진에 비해 더 적절한 검색 결과 세트를 만들기 위해 사용될 수 있습니다.현재 Clustery와 같은 웹 기반 클러스터링 도구가 많이 있습니다.또한 검색어가 매우 다른 것을 나타낼 수 있는 경우 보다 포괄적인 결과 집합을 반환하는 데 사용할 수도 있습니다.이 용어를 사용할 때마다 고유한 결과 클러스터에 대응하므로 랭킹 알고리즘이 각 ^[54]클러스터에서 상위 결과를 선택하여 포괄적인 결과를 반환할 수 있습니다.

슬립 맵 최적화

Flickr의 사진 지도와 다른 지도 사이트에서는 지도상의 마커 수를 줄이기 위해 클러스터링을 사용합니다.이것에 의해, 보다 고속이 되는 것과 동시에, 시각적 혼란을 경감할 수 있습니다.

컴퓨터 공학

소프트웨어의 진화

클러스터링은 분산되어 있는 기능을 개혁함으로써 코드의 레거시 속성을 줄이는 데 도움이 되기 때문에 소프트웨어 진화에 도움이 됩니다.이것은 구조 조정의 한 형태이며, 따라서 직접적인 예방적 유지보수의 한 방법이다.

이미지 세그멘테이션

클러스터링을 사용하면 경계 감지 또는 객체 ^[55]인식을 위해 디지털 이미지를 다른 영역으로 분할할 수 있습니다.

진화 알고리즘

군집화는 진화하는 종이나 아종 사이에 생식 기회가 보다 균등하게 분포될 수 있도록 진화 알고리즘의 개체군 내에서 다른 틈새를 식별하기 위해 사용될 수 있다.

추천 시스템

추천 시스템은 사용자의 취향에 따라 새로운 아이템을 추천하도록 설계되었습니다.클러스터링 알고리즘을 사용하여 사용자의 클러스터에 있는 다른 사용자의 환경설정을 기반으로 사용자의 환경설정을 예측하는 경우도 있습니다.

마르코프 연쇄 몬테카를로 방법

클러스터링은 표적 분포에서 극단점을 찾아 특징짓기 위해 종종 사용됩니다.

이상 검출

이상/불일치는 일반적으로 명시적이든 암묵적이든 데이터 클러스터링 구조와 관련하여 정의됩니다.

자연어 처리

클러스터링을 사용하여 어휘적 ^[54]모호성을 해결할 수 있습니다.

사회과학

사회과학에서의 시퀀스 분석

클러스터 분석은 예를 들어 가족의 삶의 궤적, 직업 경력, 일일 또는 주간 시간 사용 패턴을 식별하기 위해 사용됩니다.

범죄 분석

클러스터 분석을 사용하여 특정 유형의 범죄가 더 많이 발생하는 영역을 식별할 수 있습니다.이와 같이 특정 기간 동안 유사한 범죄가 발생한 지역이나 "핫 스폿"을 식별함으로써 법 집행 자원을 보다 효과적으로 관리할 수 있습니다.

교육 데이터 마이닝

예를 들어, 클러스터 분석은 유사한 속성을 가진 학교 또는 학생 그룹을 식별하는 데 사용됩니다.

타이폴로지

Pew Research Center와 같은 프로젝트는 여론조사 데이터를 통해 클러스터 분석을 통해 정치 및 마케팅에 유용할 수 있는 의견, 습관 및 인구통계 유형을 식별합니다.

다른이들

필드 로보틱스

클러스터링 알고리즘은 로보틱 상황 인식에 사용되어 객체를 추적하고 센서 ^[56]데이터의 특이치를 탐지합니다.

수리 화학

예를 들어 구조적 유사성 등을 찾기 위해 90개의 ^[57]위상지수 공간에 3000개의 화학성분을 집속시켰다.

기후학

기상 조건 또는 선호하는 해수면 압력 대기 ^[58]패턴을 찾습니다.

자금

클러스터 분석은 재고를 ^[59]섹터로 클러스터링하는 데 사용되어 왔습니다.

석유 지질학

군집 분석은 결측 맨 아래 구멍 코어 데이터 또는 결측 로그 곡선을 재구성하여 저장소의 특성을 평가하는 데 사용됩니다.

지구 화학

서로 다른 표본 위치에 있는 화학 성질의 군집화.

「 」를 참조해 주세요.

클러스터 분석의 특수한 유형

• 자동 클러스터링 알고리즘
• 균형 잡힌 클러스터링
• 고차원 데이터 클러스터링
• 개념 클러스터링
• 컨센서스 클러스터링
• 제약 클러스터화
• 커뮤니티 검출
• 데이터 스트림 클러스터링
• HCS 클러스터링
• 시퀀스 클러스터링
• 스펙트럼 클러스터링

클러스터 분석에 사용되는 기술

• 인공신경망(ANN)
• 가장 가까운 네이버 검색
• 근린 성분 분석
• 잠복 클래스 분석
• 어피니티 전파

데이터 투영 및 전처리

• 치수 축소
• 주성분 분석
• 다차원 스케일링

다른.

• 클러스터 가중 모델링
• 차원의 저주
• 데이터 집합의 클러스터 수 결정
• 평행 좌표
• 구조화 데이터 분석

레퍼런스