상호 정보

정보 이론
엔트로피 미분 엔트로피 조건부 엔트로피 관절 엔트로피 상호 정보 조건부 상호 정보 상대 엔트로피 엔트로피율 이산점 밀도 제한
점근 등분할 특성 속도 왜곡 이론
섀넌의 소스 부호화 정리 채널 용량 노이즈 채널 부호화 정리 섀넌-하틀리 정리
v t

확률론과 정보론에서, 두 랜덤 변수의 상호 정보(MI)는 두 변수 간의 상호 의존성에 대한 척도이다.보다 구체적으로 말하면, 다른 랜덤 변수를 관찰함으로써 하나의 랜덤 변수에 대해 얻을 수 있는 "정보의 양(shannons(비트), nats 또는 hartleys 등의 단위)"을 정량화합니다.상호 정보의 개념은 랜덤 변수의 엔트로피 개념과 밀접하게 연관되어 있으며, 랜덤 변수에 보유되는 예상 "정보량"을 수량화하는 정보 이론의 기본 개념이다.

실수치의 확률 변수와 상관 계수처럼 선형 의존성에 국한되지 않고, MI고(X, Y){\displaystyle(X,Y)}X{X\displaystyle}, Y{Y\displaystyle}. MI은 지수 함수의 한계 분배를 제품에서 한쌍의 얼마나 다르게 합동 분포를 결정한다.그pointwise 상호 정보(PMI)의Ected 값입니다.

비록 그가"상호 정보"라고 부르지 않은 수량과 분석한 클로드 섀넌에 의해 자신의 획기적인 종이" 관한 이론 통신의"에서 정의되었다.이 용어는 나중에 로버트 파노에 의해 만들어졌다.[2]상호 정보도 정보를 이득으로 알려져 있다.

정의.

$({\displaystyle }$ ${\displaystyle X}$,${\displaystyle }$$Y$ ) { $style$$( X$ ,$Y$$$)$$${\displaystyle display}$ 、 $X{\displaystyle \mathcal{}}$ $}$\ times { $mathcal {$$X$$}$ \ times { Y$$}$$$displaydisplaydisplaydisplay$ displaydisplaydisplay displaydisplaydisplaydisplaydisplay displaydisplaydisplaydisplay ${\displaystyle {\mathrm{displaydisplaydisplaydisplaydisplaydisplay}}_{}}$$$ $displaydisplaydisplaydisplaydisplaydisplaydisplaydisplay$ displaydisplaydisplaydisplaydisplaydisplaydisplay displaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplay $displaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplay$$디스플레이 스타일 P_{$$Y$ 상호 정보는 다음과 같이 정의됩니다.

${\displaystyle {여기}_{}}$서 ${\displaystyle {\mathrm{DK}}_{}}$ L$(\${KL$}})$은 Kullback-Leibler 발산입니다.

Kullback-Leibler divergence의 속성에 따라, 합동 분포가 한계값의 곱과 $일치$할 때(즉$,$ X\$displaystyle$ X$$$$$\$와 Y$\$$displaystyle$ Y$\)$${\displaystyle }$I($X;Y)$는 정확히 0이라는 $점$에 유의하십시오$.$$X에$ 내용은 없습니다$.$$)$ {$style$ I$(X;Y)}$은 음수가 아닙니다.실제로 음수가 아닌 독립 랜덤 변수 쌍으로 $($ Y) {style$(X, Y)}$을$({\displaystyle }$를) 하기 위한 가격을 측정한 것입니다.

자연 로그를 사용하는 경우 상호 정보의 단위는 nat입니다.로그 기반 2를 사용하는 경우 상호 정보의 단위는 비트라고도 하는 섀넌입니다.로그 베이스 10을 사용하는 경우, 상호 정보의 단위는 ban 또는 dit이라고도 하는 hartley입니다.

PMFs의 개별 분포 면에서요.

두 개의 이산 랜덤 $변수{\displaystyle }$X(\$displaystyle$ X$)$와 Y$(\displaystyle$ Y$)$의 상호 정보는 이중 ^{[3]: 20} 합으로 계산됩니다.

$여기$서 P${\displaystyle {(X,}_{}}$ $)$ {{$displaystyle$ $P_{(X, Y)}$는 X$(style$X)와 Y$(displaystyle$ Y$)$의 $결합{\displaystyle }$ 확률 질량 $함수$이며, ${\displaystyle P_{}}$ X$($$displaystyle$ $P_{X}$와 $($)는$$$X-style{\displaystyle }$ X-display의 $한계{\displaystyle }$ 확률 질량 함수입니다.각각 다음과 같다.

PDF파일의 지속적인 분포 면에서요.

합동으로 연속된 랜덤 변수의 경우 이중 합계는 이중 ^{[3]: 251} 적분으로 대체됩니다.

$여기$서 P${\displaystyle {(X,}_{}}$ $)$ {{$displaystyle$ $P_{(X, Y)}$는 X$(\displaystyle$X)와$$Y(\$displaystyle$Y$)$의 $공동{\displaystyle }$ 확률 밀도 $함수$이며, ${\displaystyle {PX}_{}}$$(\$$displaystyle P_{X}$와 $(\$는 $X-styledisplay$의 한계 확률 밀도 $함수$입니다.$각각 Y형$입니다.

동기

직감적으로 상호 정보는$$X$(\$displaystyle $X)$와 Y(\$displaystyle$ Y$)$가 $공유$하는 정보를 측정합니다.이러한 변수 중 하나를 알면 다른 변수에 대한 불확실성이 얼마나 감소하는지 측정합니다.예를 들어 X$(디스플레이$ 스타일 $X)$와 Y$(디스플레이 스타일$ Y$)$가 독립되어 있는 $경우{\displaystyle }$ X$(디스플레이 스타일$ X$)$를 알면 Y$(디스플레이 스타일$ Y$)$에 $대한{\displaystyle }$ 정보가 제공되지 않으므로 상호 정보는 0이 됩니다.한편, X$(style$ X$)$가 Y$(\displaystyle$ Y$)$의 결정론적 $함수$이고 $Y(\$$displaystyle$ Y$)$가 X(\$displaystyle$X$)$의 결정론적 함수인 $경우{\displaystyle }$ X($displaystyle$ Y$)$에 $의해{\displaystyle }$ 전달되는 모든 정보는$$$Y$(\$displaystyle$ X$)$ dete와$$ $공유$됩니다$.$Y$(\displaystyle$ Y$)$의 $값$을 제한하거나 Y(\displaystyle Y)의 값을 반대로 설정합니다.그 결과, 이 경우 상호 정보는$$Y$($$또는$ $X($$또는$ X)에만 포함되는 불확실성, 즉 Y$($$또는{\displaystyle }$ X$(또는$ X$)$의 엔트로피와 동일합니다.또한 이 상호정보는$X의$$$엔트로피 및$Y$의$$엔트로피와 동일하다($X$와$Y$가 같은$$ 랜덤 변수인 $경우$는 매우 특별한 경우이다).

상호 정보는 독립성을 가정하여 X$($디스플레이 스타일 X$)$와 Y$($$디스플레이 스타일$ Y$)$의 $한계{\displaystyle }$ 분포에 대해 X$($$디스플레이 스타일$ X$)$와 Y($디스플레이 스타일$ Y$)$의 공동 분포에서 표현되는 고유 의존성의 척도이다.따라서 상호 정보는 다음과 같은 의미에서 의존성을 측정합니다.${\displaystyle }$X$(style$ X$$$)$ 및 $(\displaystyle$ Y$)$가 독립적인 랜덤 변수인 $경우$에만 I${\displaystyle (X;Y}$)$=$;displaystyle $\operatorname {I}(X;Y$)=$0)$입니다.이것은 한 방향으로 쉽게 알 수 있습니다.X$(\displaystyle$X)와$$Y(\$displaystyle$ Y$)$가 $독립적$이라면 $p{\displaystyle {}_{(X},{}_{}}$Y${\displaystyle )}$ ${\displaystyle =}$ ${\displaystyle p_{}}$ X${\displaystyle {}_{}x}$ ${\displaystyle ){}_{}}$ p $)$ {$displaystyle p_{(X,Y)}$=$p_{X}(X,Y}(\CD$} $p_ot$

$\displaystyle \log {p_{(X,Y)}(x,y)}{p_{X}(x),p_{Y}(y)}\right}=\log 1=0.}$

또한 상호정보는 음이 아니다(${\displaystyle 즉}$, I ${\displaystyle (}$ (${\displaystyle }$X${\displaystyle }$; Y )${\$ ${\displaystyle 0}$ {$I }$ ( X ; ${\displaystyle Y}$$$) \ $geq$ 0$$） $symmetric{\displaystyle \mathrm{}}$ ( ( ( ( （ X${\displaystyle }$; ${\displaystyle Y}$）$$ ${\displaystyle I}$ ($Y$ ; x$$) style {$opername }$ 。

특성.

Nonnegativity

상호정보의 정의에 관한 젠슨의 부등식을 사용하여 I ${\displaystyle (}$ ( ${\displaystyle X}$;${\displaystyle Y}$) \ $displaystyle \operatorname { I$} ($X$ ; $Y$)가$$ 음이 $아님$을 알 수 있다.^{[3]: 28}

${\displaystyle\operatorname{I}(X;Y)\geq 0}$

대칭

${\displaystyle \operatorname {I}(X;Y)=\operatorname {I}(Y;X)}$

아래와 같이 엔트로피와의 관계를 고려하여 증명한다.

및 합동 조건부 엔트로피와의 관계.

상호 정보는 다음과 같이 동등하게 표현될 수 있습니다.

${\displaystyle {begin{aligned}\operatorname {I}(X;Y)&{}\equiv \mathrm {H}(X)-\mathrm {H}(Y)\equiv \mathrm {H}(Y\mid)&{equ}$

$여기$서 H${\displaystyle (}$$X$$)$ {$displaystyle \mathrm {H}(X$$)}$ $및{\displaystyle \mathrm{}}$ H${\displaystyle (Y}$$)$ {$displaystyle$$$$\$$mathrm {H$$}(Y$$)}$은 한계 $엔트로피$입니다$.$$$ $X($디스플레이 스타일 $X)$와 Y$(디스플레이 스타일$ Y$)$의 조인트 엔트로피입니다.

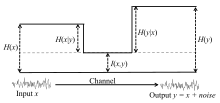
두 세트의 합집합, 차이 및 교집합에 대한 유추에 주목해 주십시오.이 점에서 위의 공식은 모두 기사의 첫머리에 보고된 벤 다이어그램에서 알 수 있습니다.

출력 $(\displaystyle$ Y$)$가 $입력{\displaystyle }$ X$(\displaystyle$ X$)$의 노이즈 버전인 통신 채널의 관점에서 다음 관계가 그림에 요약되어 있습니다.

I ${\displaystyle (}$ ( ${\displaystyle X}$;$$ )$$（ \ $displaystyle \operatorname${ I$（$X ; $Y$） ）는 ${\displaystyle 음}$이 아니기 $때문$에, H ( X${\displaystyle )\ge }$H ( ${\displaystyle Xy}$Y $){$ $displaystyle$\$mathrm${$H$} ( $X$)\ $geq$\ $modrm${$H$} ($X here$ Y )는 음이하의 값을 $나타내고{\displaystyle \mathrm{}}$ 있습니다$.$$\mid$ X$)},$ 공동으로$$ 이산 랜덤 변수의 경우:

$Y}(y)\\&.{}=\sum _{x\in\mathcal {X}, y\in\mathcal {Y}}p_{x}(x)p_{Y\mid X=x}(y)\log p_{Y\mid X=x}(y)-\sum _{x\in\mathcal {X}, y\in\mathcal {Y}p_{(X,Y)}(x,y)\log p_{Y}(y)=\sum _{x\in\mathcal {X}p_{X}(왼쪽)Y\mid X=x}(y)\log p_{Y\mid X=x}(y)\right)-\sum _{y\in\mathcal {Y}\left(\sum _{x\in\mathcal {X}}p_{(X,Y)\right)\log p_{Y}(y)\&{\sum {\mathcal {\cal {\}\\\end {aligned}}$

위의 다른 정체성의 증명은 유사하다.(단순히 이산적인 것이 아니라) 일반적인 경우의 증명은 비슷하며, 적분이 합계를 대체한다.

직관적으로 $엔트로피{\displaystyle \mathrm{}}$ H$Y)$ {\displaystyle \$mathrm {H}(Y)}$을(를) 랜덤 변수에 대한 불확실성의 척도로 $간주$하면 H${\displaystyle (Y}$ ${\displaystyle \mathrm{this}}$X${\displaystyle )}$ ${\displaystyle \mathrm {H}(Y\mid$ X$)$는$$X$(\$$displaystyle$ X$)$가 이 Y$(\displaystyle$ Y)에 $대해{\displaystyle }$ 말하지 않는 것을 $나타내는{\displaystyle }$ 척도입니다.$t{\displaystyle }$ Y는$$X$({displaystyle$X}) $이후$이므로, 두 번째 등식의 오른쪽은 "Y$(\displaystyle$Y$)$의 불확실성 양에서 X$(\displaystyle$ X$)$ 이후$$ $남은{\displaystyle }$$$Y(\$displaystyle$ Y$)$의 불확실성 양을 뺀 값"으로 해석할 수 있다.o "X$\displaystyle$ X$"$를 알면 제거되는 Y$\displaystyle$의 불확실성 양"이는 어느 한 변수를 아는 것이 다른 변수에 대해 제공하는 정보의 양(즉, 불확실성의 감소)으로서 상호 정보의 직관적인 의미를 뒷받침한다.

개별 $케이스{\displaystyle \mathrm{}}$ H${\displaystyle (Yy}$ Y${\displaystyle )}$ $=$(\$displaystyle \mathrm {H$$}($$Y\mid$ Y)=$0{\displaystyle \mathrm{}}$$}$이므로 H(Y$$${\displaystyle )}$ $=$ I $)$ \$displaystyle \mathrm$ {$H}(Y)=\operatorname {I}(Y;Y$는 $다음$과 같습니다.변수는 적어도 다른 변수가 제공할 수 있는 만큼의 정보를 포함합니다.

Kullback–Leibler 발산에 관계

공동으로 이산 또는 공동으로 연속되는 쌍$({\displaystyle X,}$ $)$의 경우({displaystyle $(X, Y$ 상호정보는 $한계분포$의 곱(${\displaystyle {}_{}}$ ${\displaystyle X_{}{y}_{}}$P Y \$displaystyle p_{X$}\$cdot$p_{})에서 Kullback-Leibler 발산이다.$Y$ 조인트 $분포{\displaystyle {}_{}}$ p${\displaystyle {(X,}_{}}$ $)$의 {{displaystyle $p_{(X, Y$ 즉,

또한 p ${\displaystyle {Xy}_{}}$ Y ${\displaystyle {=}_{}{y}_{}}$ (${\displaystyle x}$ ) ${\displaystyle ={}_{}}$ (${\displaystyle X}$ ,${\displaystyle Y}$) / ${\displaystyle p_{}}$Y (${\displaystyle y}$) ( y ) { $display p$_ {$X$ \ $mid$ Y =$y$} ( x ) =$$p _ { ( X , Y ) } ($x$ , y ) =$$p _ { ( X , Y ) } /$p$ _ p _ { x , $y$} ( x , y )로 한다.그럼, 우린 그 아이덴티티를 가지고 있어

합동 이산 랜덤 변수에 대한 증명은 다음과 같습니다.

${\displaystyle {displaystyle {aligned}\operatorname {I}(X;Y)&=\sum _{y\in {mathcal {X}}{p_{(X,Y)}\log \left\fracp_{X,Y}(X,Y}){x}}\\&=\sum _{y\in\mathcal {Y}\sum _{x\in\mathcal {X}}p_{X\mid Y=y}(x)\log {frac {p_{X\mid Y=y}(x){X}\log {x}p_{Y}{X};D_{\text{\text}KL}}\!\left(p_{X\mid Y=y}\parallel p_{X}\오른쪽)\\&=\mathbb {E} _{Y}\left[D_{\text{}KL}}\!\left(p_{X\mid Y}\parallel p_{X}\right)\right]\end { aligned}}$

마찬가지로 이 동일성은 공동 연속 랜덤 변수에 대해 확립할 수 있습니다.

여기서 Kullback-Leibler 발산에는 랜덤 $변수{\displaystyle }$X(\$displaystyle$X)의 값만$$ 통합됩니다.식 ${\displaystyle {\text{DKL}}_{}}$( ${\displaystyle {}_{}}$ ${\displaystyle {Xy}_{}}$ Y${\displaystyle {}_{}{}_{}}$ ${\displaystyle p_{}}$ X$$ $display D_{\text${KL$}}(p_{X\mid$ Y$}\parallel p_{X})$는 여전히 랜덤 변수를 나타내기 $때문$입니다.$따라서$ 상호 정보는 $X$의$$$일변량$ $분포$ $X$의${\displaystyle {}_{}}$Kullback-Leibler diversion($Kullback-Leibler$ $diversion$$)$에 $대한$ 기대치로도 이해할 수 있다$.$$분포{\displaystyle {}_{}}$ ${\displaystyle p_{}}$ X${\displaystyle y_{}}$Y ( \ $displaystyle p$_ {$X$ \ $mid$ Y$$} )와 ${\displaystyle p_{}}$X ( \ $displaystyle$ p$_$ { $X$} )의$$ 평균 차이가 클수록 정보 이득이 커집니다.

상호 정보의 베이즈의 평가 때문이다.

공동 분포에서 표본을 구할 수 있는 경우, 베이지안 접근법을 사용하여 해당 분포의 상호 정보를 추정할 수 있다.이를 위한 첫 번째 연구는 상호 정보 외에 많은 다른 정보 이론 속성의 베이지안 추정 방법을 보여주었다.^[4]후속 연구자들은 이 분석을 다시 도출하고 확장했다.상호 정보 그 자체의 평가에 특화된 최신 문서에 대해서는 을 참조하십시오.또한 최근 연속 및 다변량 출력을 설명하는 추정 방법인 Y$\displaystyle$Y가 ^[8]에서 제안되었습니다.

독립 가설

상호 정보의 Kullback-Leibler $발산$ 공식은 p$x$ $y)$와 완전 인수 분해된 외부 곱 $($ $y$의 $비교$에 관심이 있는 것을 전제로 하고 있습니다.예를 들어, 많은 문제에서는, 음수 분해되지 않은 행렬이 $1개$ 적습니다.xtreme 인수분해. 구체적으로는 p${\displaystyle }$(${\displaystyle x}$ ,${\displaystyle y}$) { $display style$p ($x$ ,$y$ ) }를$$ 알 수 없는 $변수{\displaystyle }$ w$${\ $display style$ w$\}$의 낮은 순위 매트릭스 $근사치$와 비교하고 싶다. 즉, 어느 정도까지 p (x , y )

${\displaystyle p(x,y)\about \sum _{w}p^{\prime }(x,w)p^{\prime \prime }(w,y)}$

또는 p${\displaystyle (x}$,${\displaystyle y}$) {$displaystyle$ p$(x$, $y)}$가 인수분해를 얼마나 더 많이 수행하는지 알고 싶을 수도 있습니다.이 경우 $풀분포{\displaystyle }$ p${\displaystyle (x}$,${\displaystyle y}$)({$displaystyle p(x$, y)}가$$ 행렬 인수분해를 계승하는 초과정보는 Kullback-Leibler divergence에 의해 주어집니다.

${\displaystyle \operatorname {I}_{LRMA}=\sum_{y}\sum_{x\in\mathcal {X}}{p(x,y)\log\leftfrac {p(x,y)}{\sum_w}{prime}{prime}{p}{prime}{p}$

상호 정보에 대한 기존의 정의는 프로세스$W$의 $값$이 $\displaystyle$w에$$대해 1개뿐인 극단적인 경우 복구됩니다.

변주곡

상호 정보에 대한 몇 가지 변형이 다양한 요구에 적합하도록 제안되어 왔다.이 중에는 정규화된 변종과 세 개 이상의 변수에 대한 일반화도 있습니다.

메트릭

많은 응용 프로그램에는 메트릭, 즉 점 쌍 간의 거리 측정이 필요합니다.수량

${\displaystyle {begin{aligned}d(X,Y)&=\mathrm {I}(X;Y)\&=\mathrm {H}(X)+\mathrm {H}(Y)-2\operatorname {I}(X=Y)&\mathrm {I}(X;Y)$

는 메트릭의 특성(부등식, 비부정성, 무차별성 및 대칭성)을 충족합니다.이 거리 메트릭은 정보의 변동이라고도 합니다.

X${\displaystyle ,}$ $(\displaystyle$ X$,$${\displaystyle Y}$$)$가 이산 랜덤 변수인 $경우{\displaystyle }$ 모든 엔트로피 항은 음이 아닙니다. $따라서{\displaystyle \mathrm{}}$ ${\displaystyle 0(}$ ${\displaystyle d}$( X${\displaystyle }$, Y )${\displaystyle (}$ ${\displaystyle H}$( ${\displaystyle X}$, Y$$) \ $displaystyle 0$ \ $leq d$( X , Y ) \$leq$ \$mathrm { H$（ X , Y$$） one$$ $one$ one one one one qizedized if if if q if if if if q if if if if if if q if if if if q if if if if q q q ${\displaystyle q\mathrm{}}$ q if if if if if q if

${\displaystyle D(X,Y)=frac {d(X,Y)}{\mathrm {H}(X,Y)}}\leq 1.}$

$메트릭{\displaystyle }$ D$(표시$ 스타일$$D)는$$ 범용 메트릭으로, 다른 거리 측정이 X$(표시 스타일$ X$)$와 Y$(표시 스타일$ Y$)$를 $근접$하게 배치하면$$D($표시$ 스타일 D$)$도 ^{[9][dubious – discuss]}근접하게 판단합니다.

정의를 연결하면 다음과 같이 표시됩니다.

${\displaystyle D(X,Y)=1-{\frac {operatorname {I}(X;Y)}{\mathrm {H}(X,Y)}}}$

이것은 라즈키 거리라고 알려져 있다.^[10]설정 이론적인 정보 해석(조건부 엔트로피 그림 참조)에서는 X$(\displaystyle$ X$)$와 Y$(\displaystyle$ Y$)$ $사이$의 Jaccard 거리입니다.

마침내.

${\displaystyle D^{\prime }(X,Y)=1-{\frac {operatorname {I}(X;Y)}{\mathrm {H}(X)\mathrm {H}(Y)\right\}}}}$

는 메트릭이기도 합니다.

조건부 상호 정보

세 번째 변수에서 조건화된 두 랜덤 변수의 상호 정보를 표현하는 것이 유용할 수 있습니다.

합동 이산 랜덤 변수의 경우 다음과 같은 형식을 취합니다.

$\displaystyle \operatorname {I}(X;Y Z)=\sum _{z\in {mathcal {Z}}\sum _{y\in {mathcal {Y}}\sum _{x\in {X}}{p_{Z}(z},p_{X,YZ}\log\y)$

라고 간단히 말할 수 있다

$\displaystyle \operatorname {I}(X;Y Z)=\sum_{z\in\mathcal {Z}}\sum_{y\in\mathcal {X}}\sum_{x\in\mathcal {X}}p_{X,Y}\log_FRAC {X}$

합동 연속 랜덤 변수의 경우 다음과 같은 형식을 취합니다.

${\displaystyle \operatorname {I}(X;Y Z)=\int _{\mathcal {Z}\int _{\mathcal {Y}}\int _{\mathcal {X}{Z}(z), p_{X,Y Z}\log \[\frAC {\fr}$

라고 간단히 말할 수 있다

${\displaystyle \operatorname {I}(X;Y Z)=\int _{\mathcal {Z}\int _{\mathcal {Y}}\int _{X,Y,Z}\log {frac {p_{X,Y,Z},X}\int}$

세 번째 랜덤 변수에 따라 조정하면 상호 정보가 증가하거나 감소할 수 있지만 항상 다음과 같습니다.

${\displaystyle \operatorname {I}(X;Y Z)\geq 0}$

이산, 공동 분포 랜덤 변수 $X{\displaystyle ,}$ ${\displaystyle Y,}$ $(\displaystyle$ X,$Y, Z$ 이 결과는 정보 이론의 다른 불평등을 증명하기 위한 기본 구성 요소로 사용되어 왔다.

상호 작용 정보

두 개 이상의 랜덤 변수에 대한 상호 정보의 몇 가지 일반화가 제안되었다. 예를 들어, 총 상관 관계(또는 다중 정보)와 이중 총 상관 관계가 그것이다.다변량 고차 상호 정보의 표현과 연구는 두 개의 독립적인 작품인 McGill(1954년)^[11]과 Hu Kuo Ting(1962년)^[12]에서 이루어졌다.하나의 변수에 대해 다음과 같이 상호 작용 정보가 정의됩니다.

${\displaystyle \operatorname {I}(X_{1})=\mathrm {H}(X_{1})}$

n>의 $,$ {\$displaystyle$ n > $1,}$

${\displaystyle \operatorname {I}(X_{1};,...;X_{n})=\operatorname {I}(X_{1};,...,X_{n-1})-\operatorname {I}(X_{1};,...,X_{n-1},X_{n})_{N}.}$

일부 저자들은 앞의 방정식의 오른쪽에 있는 항의 순서를 반대로 합니다.이것은 랜덤 변수의 수가 홀수일 때 부호를 바꿉니다.(그리고 이 경우, 단일 변수 식은 엔트로피의 음수가 됩니다.)주의:

$({displaystyle I(X_{1};\ldots;X_{n-1}\mid X_{n})=\mathbb {E}_{X_{n}}[D_{\mathrm {KL}}}(P_{X_{1},\ldots,X_{n-1}\mid}) p_N})}$

다변량 통계 독립성

다변량 상호 정보 함수는 I${\displaystyle ({X\mathrm{}}_{}}$1 ; ${\displaystyle {}_{}{2\mathrm{}}_{}}$) $=$ $(X_{1};X_{$2$}),$ 임의 $변수$인 ${\displaystyle {경우}_{}}$에만${\displaystyle {}_{}{X\mathrm{}}_{}}$ 1, ${\displaystyle {}_{}}$ 2$($ 스타일 $X_{$1}; $X_${2}=$0$를 나타내는 쌍별 독립 사례를 일반화합니다.n개의 변수는 ${\displaystyle \mathrm{2개}}$의 n${\displaystyle {}^{}}$-${\displaystyle n}$ -$$(\$displaystyle$ 2$^{n}-n-1)$ $상호$ 정보 함수가${\displaystyle }I{\displaystyle }$(${\displaystyle {X\mathrm{}}_{}}$1${\displaystyle }$; ${\displaystyle ...}$ ; ${\displaystyle X_{}}$k ) ${\displaystyle =}$(\$displaystyle$ I$(X_{1};\ldots;X_{k$}) ${\displaystyle =}$$0$(\$displaystyle nq$ $$2$)$인 경우에만 상호 독립적입니다.$이러한{\displaystyle }$ 의미에서 I${\displaystyle }$( ${\displaystyle {X\mathrm{}}_{}}$1${\displaystyle }$; ${\displaystyle ...}$ ; ${\displaystyle {}_{}{k}_{}}$ ) $=$ { $displaystyle$ I$(X_{1};\ldots;X_{k$}=$0}$을 정교한 통계 독립성 기준으로 사용할 수 있다.

적용들

3가지 변수에 대해 브레너 등은 다변량 상호 정보를 신경 부호화에 적용했고 그 음성을 "시너기(synergy)"라고 불렀고 왓킨슨 등은 이를 유전자 ^[15]발현에 적용했다.임의 k 변수의 경우, Tapia 등은 유전자 ^[16][13]발현에 다변량 상호 정보를 적용했다.제로, 플러스 또는 ^[12]마이너스입니다.양의 값은 쌍별 상관관계를 일반화하는 관계에 대응하고, 무효 값은 독립성의 정교한 개념에 대응하며, 음의 값은 고차원적인 "발생" 관계와 클러스터화된 데이터 포인트를 검출합니다.

공동분포와 다른 목표변수 사이의 상호정보를 최대화하는 하나의 고차원 일반화 스킴은 특징선택에 ^[17]유용한 것으로 밝혀졌다.

신호 처리 영역에서도 상호 정보가 두 신호 간의 유사성을 측정하는 척도로 사용됩니다.예를 들어, FMI 메트릭은^[18] 소스 이미지에 대한 퓨전 이미지에 포함된 정보의 양을 측정하기 위해 상호 정보를 사용하는 이미지 퓨전 성능 측정값입니다.이 메트릭의 Matlab 코드는 ^[19]다음 위치에서 찾을 수 있습니다.n개의 변수 데이터 집합에서 모든 다변량 상호 정보, 조건부 상호 정보, 공동 엔트로피, 전체 상관 관계, 정보 거리를 계산하기 위한 파이썬 패키지를 사용할 ^[20]수 있다.

지시된 정보

$지시$된 정보, I${\displaystyle }$display ( ${\displaystyle X^{}}$ n ${\displaystyle {}^{}}$ ${\displaystyle {}^{}{n}^{}}$) { $displaystyle \operatorname { I$} \$left$($X$^ { $n$} \ $to$ Y ^ { $n$$$}$$$\}$ } ${\displaystyle {displaydisplaydisplaydisplay}^{}}$ $、$ X $style$ ${\displaystyle {displaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplay}^{}}$ 、 X style$$（ \ $display$ X $）$ 。${\displaystyle ,}$ .${\displaystyle }$. , ${\displaystyle X_{}}$ { $style$ X _ {$1}$ , $X$_ {$n$$$} 、 ${\displaystyle Y^{}}$n$$ { $display style$ Y^ { $n$} ${\displaystyle 、}$ ${\displaystyle {Y\mathrm{}}_{}}$ n 、 ${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ . ,${\displaystyle {}_{}}$ \ $display style$ Y _ { $1$, Y$_$ { 2 } $。$$Y_{n$지시된 정보라는 용어는 James Massey에 의해 만들어졌으며 다음과 같이 정의된다.

$display$$Y_{i}\mid$ Y$^{i-1}\right$

n ${\displaystyle =}$ ${\displaystyle 1}${$style$ n$=1$이면 $지시$된 정보가 상호 정보가 됩니다.방향 정보는 피드백이 ^[21][22]있는 채널의 용량과 같이 인과관계가 중요한 문제에 많이 적용된다.

정규화된 변형

상호 정보의 정규화된 변형은 제약,^[23] 불확실성 계수^[24] 또는 ^[25]숙련도 계수에 의해 제공된다.

${\displaystyle C_{X}Y}={operatorname {I}(X;Y)}{\mathrm {H}(Y)}}~~{\mbox{and}}~~~C_{YX}={operatorname {I}(X;Y)}{\mathrm {H}(X})}.}$

두 계수의 값 범위는 [0, 1]이지만 반드시 동일하지는 않습니다.경우에 따라서는 다음과 같은 용장성^{[citation needed]} 측정과 같은 대칭 측정이 바람직할 수 있습니다.

${\displaystyle R=paratorname {I}(X;Y)}{\mathrm {H}(X)+\mathrm {H}(Y)}}$

변수가 독립적일 때 최소 0에 도달하고 최대값은 0에 도달합니다.

${\displaystyle R_{\max} = prac {\min\left\{\mathrm {H}(X)\right\} {\mathrm {H}(X)+\mathrm {H}(Y)}}$

하나의 변수가 다른 변수를 알고 완전히 중복되는 경우.용장성(정보 이론)도 참조해 주세요.

또 다른 대칭 척도는 대칭 불확도이다(Witten & Frank 2005).

${\displaystyle U(X,Y)=2R=2{\frac {operatorname {I}(X;Y)}{\mathrm {H}(X)+\mathrm {H}(Y)}}}$

이는 2개의 불확실성 $계수{\displaystyle {}_{}}$ C ${\displaystyle X_{}}$ ${\displaystyle Y_{}}$ ${\displaystyle C_{}}$ ${\displaystyle Y_{}}$ X$({$^[24]의 조화 평균을 나타냅니다.

상호 정보를 총 상관 관계 또는 이중 총 상관 관계의 특수한 경우로 간주할 경우, 정규화된 버전은 각각 다음과 같습니다.

$I$( ${\displaystyle \frac{X}{}}$;${\displaystyle \frac{Y}{}}$ )${\displaystyle \frac{min}{}}$[${\displaystyle \frac{H\mathrm{}}{}}$ (${\displaystyle \frac{X\mathrm{}}{}}$) ${\displaystyle \frac{、}{}}$ ${\displaystyle \frac{H}{}}$(${\displaystyle \frac{}{}}$Y )$$]{ style $\ frac${ $I }$ ( X ; Y )$}{\min$ \ left [ \$mathrm { H } （$ X ; $Y$${\displaystyle \frac{}{}}$$）$ ${\displaystyle \frac{\}}{}}$ $i$ i i i i ${\displaystyle \frac{i}{}}$ i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i${\displaystyle \frac{}{}}$（ ${\displaystyle \frac{\mathrm{}}{}}$ ; ${\displaystyle \frac{Y}{}}$）

이 정규화된 버전은 IQR(Information Quality Ratio)이라고도 하며,^[26] 완전한 불확실성에 대해 다른 변수를 기준으로 변수의 정보량을 수량화합니다.

${\displaystyle IQR(X,Y)=\operatorname {E}[\operatorname {I}(X;Y)]=parac {I}(X;Y}){\mathrm {H}(X,Y)}}=parcsum {{X\in}$

상호 정보를 공분산과 유사하게 생각하는 것에서 비롯된 정규화가^[27] 있습니다(따라서 섀넌 엔트로피는 분산과 유사합니다).그런 다음 정규화된 상호 정보가 Pearson 상관 계수와 유사하게 계산됩니다.

$({displaystyle {frac {I}(X;Y)}{\sqrt {mathrm {H}(Y)}}\;}$

가중 변형

상호 정보의 전통적인 공식화에서,

${\displaystyle \operatorname {I}(X;Y)=\sum _{y\in Y}\sum _{x\in X}p(x,y)\log {p(x)},p(y)},$

$({\displaystyle x}$ ,${\displaystyle y}$) { $displaystyle ( x$ ,$y$ ) { $displaystyle$p ($x$ , $y$에 의해 지정된 각 이벤트 또는 오브젝트는 대응하는 $확률p{\displaystyle }$ ${\displaystyle (x}$ ,${\displaystyle y}$)에 의해 가중치가 부여됩니다.이것은 모든 오브젝트 또는 이벤트가 발생 확률과 동등하다고 가정합니다.단, 어플리케이션에 따라서는 특정 오브젝트나 이벤트가 다른 오브젝트보다 중요하거나 특정 연관 패턴이 다른 오브젝트보다 의미적으로 더 중요한 경우가 있습니다.

예를 들어, 결정론적${\displaystyle }$매핑${\displaystyle \{}$( ${\displaystyle 1}$ ,${\displaystyle }$1${\displaystyle }$) , (${\displaystyle 2}$,$$2${\displaystyle }$) ,${\displaystyle }$( 3${\displaystyle }$, ${\displaystyle 3}$ )$$} { $displaystyle$\ { (${\displaystyle 1}$$$,${\displaystyle }$$1$${\displaystyle }$) , (${\displaystyle 3}$ , $3$${\displaystyle }$) \ }${\displaystyle }${ $displaystyle$ \ { , 1 ,${\displaystyle }$3 , 3 , ${\displaystyle 2}$}$}$ { displaystyle \ {$1$ , 3 , 3 , $3$, $2$} } 보다 강한 것으로$$ 간주할 수 있습니다$.$이는 상호 정보가 변수 값의 고유한 순서(Cronbach 1954, Coombs, Dawes & Tversky 1970, Lockhead 1970)에 전혀 민감하지 않기 때문에 관련 변수 간의 관계 매핑 형식에 전혀 민감하지 않기 때문이다.모든 변수 값에 대한 합치성을 나타내는 앞의 관계가 뒤의 관계보다 더 강하다고 판단되는 것이 바람직하다면 다음과 같은 가중 상호 정보를 사용할 수 있다(Guiasu 1977).

${\displaystyle \operatorname {I}(X;Y)=\sum _{y\in X}w(x,y)\log {p(x,y)}{p(x,y)},{frac {p(x,y)},{y}},}$

각 변수 값의 공존 $확률$에 $가중치{\displaystyle }$ w${\displaystyle (}$${\displaystyle x}$${\displaystyle ,}$$y$ {$displaystyle$w$($$x,$$y$$)\}$를 부여합니다${\displaystyle .}$ 이를 통해 특정 확률이 다른 확률보다 다소 중요할 수 있으므로 관련 전체 또는 Prégnanz 인자를 정량화할 수 있습니다.위의 예에서는 w${\displaystyle (1,1}$)$${$displaystyle$w($1,1$$)\},$ ${\displaystyle \mathrm{w}}$${\displaystyle (}$2$,$$및{\displaystyle \mathrm{w}}$(3$)$ {$displaystyle$$$w$(3$$,3)}$에 $대해{\displaystyle }$ 상대적인 가중치를 크게 사용하면 ${\displaystyle \{(1,}$ ${\displaystyle 1}$,${\displaystyle 2}$,${\displaystyle }$3$)$ ${\displaystyle \mathrm{관계}}$에 대한 보다 높은 정보를 평가할 수 있습니다$.$${$ ( 1, ${\displaystyle \mathrm{3<img\; alt="\backslash \{(1,1),(2,2),(3,3)\backslash \}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/8b13cd0103f9e43410e877754765a7ad994fe3cc"\; style="vertical-align:\; -0.838ex;\; width:19.897ex;\; height:2.843ex;">}}$ ) ,${\displaystyle }$( ${\displaystyle 2}$,${\displaystyle 1}$) ,${\displaystyle }$( ${\displaystyle 3}$,${\displaystyle 2}$)$$, ( 3 , 2 ) } { $displaystyle$ \ { ( 1 , 3 ,$1$ ) , ( 2 , 1 ) , ($3$ ,$$2 )$$\ } ${\displaystyle 。\mathrm{이것}}$은 패턴 인식 등의 경우에 바람직할 수 있습니다.이 가중치 상호정보는 가중치 KL-Divergence의 한 형태로 일부 입력에 ^[28]음의 값을 취하는 것으로 알려져 있으며 가중치 상호정보가 음의 값을 취하는 ^[29]사례도 있다.

조정된 상호 정보

확률 분포는 집합의 분할로 볼 수 있습니다.그런 다음 한 집합이 무작위로 분할될 경우 확률 분포는 어떻게 됩니까?상호정보의 기대치는?조정된 상호 정보(AMI)는 MI의 기대치를 차감하기 때문에 서로 다른 두 분포가 랜덤한 경우 AMI가 0이고 두 분포가 동일한 경우 AMI가 0입니다.AMI는 세트의 서로 다른 두 파티션의 조정된 랜드 지수와 유사하게 정의됩니다.

절대 상호 정보

콜모고로프 복잡도 개념을 사용하면 확률 분포와는 무관하게 두 시퀀스의 상호 정보를 고려할 수 있다.

$\displaystyle \operatorname {I} _{K}(X;Y)=K(X)-K(X\mid Y).}$

이 양이 최대 로그 계수(${\displaystyle I_{}}$ K ${\displaystyle (}$ (${\displaystyle X}$ ;${\displaystyle Y}$ )${\displaystyle {\mathrm{}}_{}}$ ${\displaystyle I_{}}$ K${\displaystyle {}_{}(}$ (${\displaystyle Y}$ ;${\displaystyle X}$ $)\displaystyle \operatorname {I}$ _${K}(X;Y)\approx \operatorname {I} _{K}(Y;X$col 체인 규칙 1개가 필요합니다.압축에 의한 이 양의 근사치를 사용하여 시퀀스에 대한 영역지식을 전혀 가지지 않고 시퀀스의 계층적 클러스터링을 실행하는 거리측정을 정의할 수 있다(Cilibrasi 및 Vitannyi 2005).

선형 상관

곱 모멘트 상관 계수와 같은 상관 계수와 달리, 상호 정보에는 상관 계수 척도로서의 선형 종속성뿐만 아니라 선형 및 비선형 모든 종속성에 대한 정보가 포함됩니다.$그러나$X와$Y의$$$합동분포가 이변량 정규분포(특히$$ 두 한계분포가 정규분포임을 나타냄)인 좁은 경우에는 I$\displaystyle \operatorname {I}$과$($와) 상관관계 coffi $사이$에 정확한 관계가 있다.$cient{\displaystyle }${\(\$displaystyle \rho)($Gel'fand & Yaglom 1957).

${\displaystyle \operatorname {I} =-{\frac {1}{2}}\log \left(1-\rho ^{2}\오른쪽)}$

위의 방정식은 이변량 가우스에서 다음과 같이 도출할 수 있습니다.

${\displaystyle{\begin{정렬}{\begin{pmatrix}X_{1}\\X_{2}\end{pmatrix}}&\sim{{N\mathcal}}\left({\begin{pmatrix}\mu_{1}\\\mu_{2}\end{pmatrix}},\Sigma\right),\qquad\Sigma ={\begin{pmatrix}\sigma _{1}^{2}&, \rho \sigma _{1}\sigma _{2}\\\rho \sigma _{1}\sigma _{2}&, \sigma _{2}^{2}\end{pmatrix}}\\\mathrm{H}(X_{나는})&, ={\frac{1}{2}}년.로그 \left(2\pi e\flash _{i}^{2}\right)=flac {1}{2}+{\log(2\pi)+\log \left(\flac _{i}\right),\flac i\in \1,2\\\\mathrm {H}(X_1},{2})\flac {1}+{flash}.$

그러므로,

$\displaystyle \operatorname {I} \left(X_{1};X_{2}\right)=\mathrm {H} \left(X_{1}\right)+\mathrm {H} \left(X_{2}\right)-\mathrm {H} \left(X_{1},_2\right)$

이산 데이터의 경우

X$(\displaystyle$ X$)$ 및$$ $(\displaystyle$ Y$)$가 이산적인 개수로 제한되면 관측 $데이터$는 행 $변수{\displaystyle }$ X$($$또는{\displaystyle }$ i$\displaystyle$ i$)$ 및 열 $변수{\displaystyle }$ Y$($$또는{\displaystyle }$ j$\displaystyle$ j$)$로 분할 테이블에 요약됩니다.상호 정보는 행 변수와 열 변수 간의 연관성 또는 상관 관계를 측정하는 척도 중 하나입니다.기타 연관성 측도에는 Pearson의 카이 제곱 검정 통계량, G-검정 통계량 등이 포함됩니다.실제로 상호정보는 G-test 통계정보를 $({displaystyle 2N$으로 나눈 것과 같습니다. 여기서 $({displaystyle$ N$})$은 샘플 크기입니다.

적용들

많은 응용 프로그램에서 상호 정보를 최대화하려고 합니다(따라서 종속성이 증가함). 이는 종종 조건부 엔트로피를 최소화하는 것과 같습니다.예를 들어 다음과 같습니다.

• 검색엔진 기술에서는 k-평균 클러스터링을 통해 의미 클러스터(개념)^[30]를 발견하기 위한 기능으로 구문과 컨텍스트 간의 상호 정보를 사용합니다.예를 들어 빅램의 상호 정보는 다음과 같이 계산될 수 있습니다.

${\displaystyle {여기}_{}}$서 f ${\displaystyle X_{}}$Y(\$displaystyle f_{X$)$Y}}$은 bigram xy가 말뭉치에 $나타나는{\displaystyle {}_{}}$ 횟수,$$ X(\$displaystyle f_{$X$$})는 말뭉치에 나타나는 횟수, B는 bigram의 총수, U는 ^[30]unigram의 총수이다.

• 통신에서 채널 용량은 상호 정보와 동일하며, 모든 입력 분포에 걸쳐 최대화됩니다.
• 숨겨진 마르코프 모델에 대한 차별적 훈련 절차는 최대 상호 정보(MMI) 기준에 따라 제안되었다.
• 다중 배열 정렬에서 RNA 2차 구조 예측.
• 기능적으로 연결된 유전자의 쌍별 존재 및 소실로부터의 계통학적 프로파일링 예측.
• 상호 정보는 기계 학습에서 기능 선택 및 기능 변환의 기준으로 사용되어 왔습니다.최소 용장성 기능 선택 등 변수의 관련성과 용장성을 모두 나타내기 위해 사용할 수 있습니다.
• 상호 정보는 데이터 세트의 서로 다른 두 클러스터 간의 유사성을 결정하는 데 사용됩니다.따라서, 이것은 전통적인 랜드 지수보다 몇 가지 이점을 제공합니다.
• 단어들의 상호 정보는 종종 말뭉치 언어학에서 코로케이션 계산을 위한 중요한 함수로 사용된다.이 경우 단어 인스턴스가 두 개의 다른 단어에 대한 인스턴스가 아닌 두 개의 단어가 인접 또는 근접하게 발생한 경우를 계산합니다. N개의$단어$에서 $한{\displaystyle }$ 단어가 발생할 확률은$N개$의 단어에 $따라{\displaystyle }$ 올라가기 때문에 계산이 약간 복잡해집니다.$aystyle$ N$\}$ 입니다.
• 영상 등록을 위한 의료 영상촬영에는 상호 정보가 사용됩니다.기준 화상(예를 들어 뇌스캔)과 기준 화상과 동일한 좌표계에 둘 필요가 있는 제2 화상이 주어지면, 이 화상과 기준 화상과의 상호 정보가 최대화될 때까지 이 화상은 변형된다.
• 시계열 분석에서 위상 동기화 감지
• 인포맥스 기반의 독립 성분 분석 알고리즘을 포함한 신경망 및 기타 기계 학습을 위한 인포맥스 방법
• 매립 지연 파라미터를 결정하기 위해 지연 매입 정리의 평균 상호 정보를 이용한다.
• 발현 마이크로어레이 데이터에서의 유전자 간 상호 정보는 유전자 네트워크 재구성을 위한 ARACNE 알고리즘에 의해 이용된다.
• 통계역학에서 로슈미트의 역설은 ^[31][32]상호정보의 관점에서 표현될 수 있다.로슈미트는 시간 반전 대칭이 결여된 물리 법칙(예: 열역학 제2법칙)을 이러한 대칭을 갖는 물리 법칙에서만 결정하는 것은 불가능해야 한다고 지적했다.그는 볼츠만의 H이론은 기체 내 입자의 속도가 영구적으로 상관관계가 없다고 가정했고, 이로 인해 H이론에 내재된 시간 대칭이 제거되었다고 지적했다.시스템이 위상공간의 확률밀도로 설명된다면, Liouville의 정리는 분포의 결합정보(접합엔트로피의 음수)가 시간적으로 일정하게 유지된다는 것을 의미한다는 것을 보여줄 수 있다.공동 정보는 각 입자 좌표에 대한 모든 한계 정보(경계 엔트로피 음수)의 합계와 같다.볼츠만의 가정은 열역학적 엔트로피(볼츠만 상수로 나눈 값)를 산출하는 엔트로피 계산에서 상호 정보를 무시하는 것이다.
• 상호 정보는 베이지안 네트워크/동적 베이지안 네트워크의 구조를 학습하는 데 사용되며, GlobalM에 의해 예시된 것처럼 랜덤 변수 간의 인과 관계를 설명하는 것으로 생각된다.IT 툴킷:^[33] 상호 정보 테스트 기준을 사용하여 글로벌하게 최적의 동적 베이지안 네트워크를 학습합니다.
• 상호 정보는 Gibbs 샘플링 ^[34]알고리즘에서 업데이트 절차 중에 전송되는 정보를 정량화하는 데 사용됩니다.
• 의사결정 트리 학습에서 일반적인 비용 함수.
• 이 상호 정보는 은하수 동물원의 은하 특성에 대한 대규모 환경의 영향을 테스트하기 위해 우주론에서 사용됩니다.
• 상호 정보는 태양 물리학에서 태양 흑점에 대한 이동 시간 편차 지도, 정음 태양 측정에서^[35] 시간-거리 다이어그램을 도출하기 위해 사용되었다.
• 불변 정보 클러스터링에서 라벨이 지정된 데이터가 ^[36]없는 신경 네트워크 분류기 및 이미지 세그먼트(segmenter)를 자동으로 교육하기 위해 사용됩니다.

「 」를 참조해 주세요.

• 데이터 차이점 보관
• 포인트별 상호 정보
• 양자 상호 정보
• 특정 정보

메모들

레퍼런스

• Baudot, P.; Tapia, M.; Bennequin, D.; Goaillard, J.M. (2019). "Topological Information Data Analysis". Entropy. 21 (9). 869. arXiv:1907.04242. Bibcode:2019Entrp..21..869B. doi:10.3390/e21090869. PMC 7515398. S2CID 195848308.
• Cilibrasi, R.; Vitányi, Paul (2005). "Clustering by compression" (PDF). IEEE Transactions on Information Theory. 51 (4): 1523–1545. arXiv:cs/0312044. doi:10.1109/TIT.2005.844059. S2CID 911.
• Cronbach, L. J. (1954). "On the non-rational application of information measures in psychology". In Quastler, Henry (ed.). Information Theory in Psychology: Problems and Methods. Glencoe, Illinois: Free Press. pp. 14–30.
• Coombs, C. H.; Dawes, R. M.; Tversky, A. (1970). Mathematical Psychology: An Elementary Introduction. Englewood Cliffs, New Jersey: Prentice-Hall.
• Church, Kenneth Ward; Hanks, Patrick (1989). "Word association norms, mutual information, and lexicography". Proceedings of the 27th Annual Meeting of the Association for Computational Linguistics. 16 (1): 76–83. doi:10.3115/981623.981633.
• Gel'fand, I.M.; Yaglom, A.M. (1957). "Calculation of amount of information about a random function contained in another such function". American Mathematical Society Translations. Series 2. 12: 199–246. doi:10.1090/trans2/012/09. ISBN 9780821817124. Uspekhi Matematicheskikh Nauk 12의 원문 번역: 3-52.
• Guiasu, Silviu (1977). Information Theory with Applications. McGraw-Hill, New York. ISBN 978-0-07-025109-0.
• Li, Ming; Vitányi, Paul (February 1997). An introduction to Kolmogorov complexity and its applications. New York: Springer-Verlag. ISBN 978-0-387-94868-3.
• Lockhead, G. R. (1970). "Identification and the form of multidimensional discrimination space". Journal of Experimental Psychology. 85 (1): 1–10. doi:10.1037/h0029508. PMID 5458322.
• 데이비드 J. C.맥케이정보 이론, 추론 및 학습 알고리즘 케임브리지:케임브리지 대학 출판부, 2003.ISBN 0-521-64298-1(온라인에서 무료로 이용 가능)
• Haghighat, M. B. A.; Aghagolzadeh, A.; Seyedarabi, H. (2011). "A non-reference image fusion metric based on mutual information of image features". Computers & Electrical Engineering. 37 (5): 744–756. doi:10.1016/j.compeleceng.2011.07.012. S2CID 7738541.
• 아타나시오스 파풀리스.확률, 랜덤 변수 및 확률적 과정, 두 번째 판.뉴욕: McGraw-Hill, 1984. (15장 참조)
• Witten, Ian H. & Frank, Eibe (2005). Data Mining: Practical Machine Learning Tools and Techniques. Morgan Kaufmann, Amsterdam. ISBN 978-0-12-374856-0.
• Peng, H.C.; Long, F. & Ding, C. (2005). "Feature selection based on mutual information: criteria of max-dependency, max-relevance, and min-redundancy". IEEE Transactions on Pattern Analysis and Machine Intelligence. 27 (8): 1226–1238. CiteSeerX 10.1.1.63.5765. doi:10.1109/tpami.2005.159. PMID 16119262. S2CID 206764015.
• Andre S. Ribeiro; Stuart A. Kauffman; Jason Lloyd-Price; Bjorn Samuelsson & Joshua Socolar (2008). "Mutual Information in Random Boolean models of regulatory networks". Physical Review E. 77 (1): 011901. arXiv:0707.3642. Bibcode:2008PhRvE..77a1901R. doi:10.1103/physreve.77.011901. PMID 18351870. S2CID 15232112.
• Wells, W.M. III; Viola, P.; Atsumi, H.; Nakajima, S.; Kikinis, R. (1996). "Multi-modal volume registration by maximization of mutual information" (PDF). Medical Image Analysis. 1 (1): 35–51. doi:10.1016/S1361-8415(01)80004-9. PMID 9873920. Archived from the original (PDF) on 2008-09-06. Retrieved 2010-08-05.
• Pandey, Biswajit; Sarkar, Suman (2017). "How much a galaxy knows about its large-scale environment?: An information theoretic perspective". Monthly Notices of the Royal Astronomical Society Letters. 467 (1): L6. arXiv:1611.00283. Bibcode:2017MNRAS.467L...6P. doi:10.1093/mnrasl/slw250. S2CID 119095496.