케이블 이론

그림 1: 케이블 이론의 신경 섬유에 대한 단순화된 시각

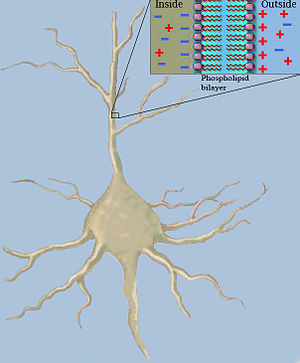
고전적인 케이블 이론은 수동 신경, 특히 다른 부위와 시간에 시냅스 입력을 받는 수지상돌기를 따라^[a] 전류(및 그에 따른 전압)를 계산하기 위해 수학적 모델을 사용합니다.추정은 덴드라이트와 축삭을 c $c_{m}$ { $디스플레이$ 스타일 $c_{m}$ 의 $c_{m}$ 용량과 $r_{m}$ r {{ $display$ $r_{$ m}}의 $r_m$ 저항을 병렬로 조합한 원통 세그먼트로 구성함으로써 이루어집니다(그림 1 참조).신경섬유의 캐패시턴스는 정전력이 매우 얇은 지질 이중층을 통해 작용하기 때문에 발생합니다(그림 2 참조). $r_{l}$ $r_{l}$ {\ $displaystyle r_{$ l $r_{l}$ }}을 따라 직렬로 저항이 발생하는 것은 축삭질이 전하 이동에 상당한 저항을 보이기 때문입니다.

그림 2: 파이버 캐패시턴스

역사

컴퓨터 신경과학의 케이블 이론은 윌리엄 톰슨 교수(나중에 켈빈 경으로 알려짐)가 해저 전신 케이블의 신호 붕괴의 수학적 모델을 개발하기 시작한 1850년대로 거슬러 올라간다.이 모델은 와이어의 열 전도를 설명하기 위해 푸리에가 사용한 편미분 방정식과 유사했습니다.

1870년대에 헤르만은 열전도와의 유추에 초점을 맞춤으로써 신경전위(electrotonic potentials)를 모형화하려는 첫 시도를 보았다.하지만, 1898년 켈빈의 해저 케이블과의 유추를 처음 발견한 후, 20세기 초에 신경섬유 케이블 이론을 독자적으로 개발한 사람은 헤르만과 크레머였다.케이블 이론에 기초한 신경섬유 전도의 수학적인 이론은 콜과 호지킨, 오프너 외 연구진(1940), 러쉬튼(1951)에 의해 개발되었다.

축삭의 거동을 모델링하는 데 케이블 이론의 중요성에 대한 실험적인 증거는 1930년대에 콜, 커티스, 호지킨, 버나드 캐츠 경, 러쉬튼, 타사키 등에 의해 표면화되기 시작했다.데이비스와 로렌테 드 노(1947년)와 호지킨과 러쉬턴(1946년)이 이 시대의 두 주요 논문이다.

1950년대는 개별 뉴런의 전기 활동을 측정하는 기술이 향상되었다.따라서 케이블 이론은 세포 내 미세 전극 기록에서 수집된 데이터를 분석하고 신경 수지상돌기의 전기적 특성을 분석하는 데 중요해졌다.Coombs, Eccles, Fatt, Frank, Fuortes와 같은 과학자들은 뉴런의 기능적 통찰력을 얻고 새로운 실험의 설계에서 그들을 이끌기 위해 케이블 이론에 크게 의존했다.

나중에, 수학적 파생물을 이용한 케이블 이론은 잭, 랄, 레드맨, 린젤, 이다 세게브, 턱웰, 벨, 그리고 이안넬라와 같은 근로자들에 의해 훨씬 더 정교한 뉴런 모델을 탐구할 수 있게 해주었다.보다 최근에는 케이블 이론이 뇌의 ^[1]백질에서 다발 뉴런의 e-전자 활성 모델에 적용되고 있다.

케이블 방정식 도출

r에는_m 다양한 규칙이 있습니다.여기서_m r과_m c는 위에서 소개한 바와 같이 막길이 단위(m당)로 측정한다.따라서_m r은 ohm·meters(Ω·m) 단위로_m, c는 parads per meter(F/m) 단위로 측정된다.이는 막의 단위 면적(m²)의 비저항과 캐패시턴스를 각각 나타내는 R(Ω·m² 단위)과_m C(F²/m 단위)와는_m 대조적이다.따라서 축삭의 반지름 a를 ^[b]알 수 있는 경우 축삭의 둘레는 2µa, r이며_m c_m 값은 다음과 같이 계산할 수 있습니다.

r_{m}=black {R_{m}}{2\pi a\}

(1)

c_{m}=C_{m}2\pi a\

(2)

축삭의 둘레가 클수록 전하가 막을 통해 빠져나가는 면적이 커져 막 저항이 낮아지고(R을 2µa로 나눗셈_m), 전하를 저장할 수 있는 막이 많아지기 때문에(C에 2µa를 곱한_m 값) 이러한 관계는 직관적으로 의미가 있습니다.축삭질의 특정 전기저항 δ를_l 사용하면 단위 길이당 세로방향 세포내 저항 r_l(δ·m⁻¹ 단위)을 다음 방정식으로 계산할 수 있다.

r_{l}=pi frac {rho _{l}}{\pi a^{2}\}

(3)

축삭의 단면적 δa가² 클수록 축삭질을 통해 전하가 흐르는 경로의 수가 많아지고 축삭 내성이 낮아진다.

고전 케이블 이론을 확장하는 몇몇 중요한 방법들은 최근 수상돌기 내 단백질 분극의 영향과 뉴런의 수상돌기 표면에 걸친 다른 시냅스 입력 분포를 분석하기 위해 내인성 구조의 도입을 보았다.

케이블 방정식이 어떻게 도출되는지를 더 잘 이해하려면 먼저 이론 뉴런을 더욱 단순화하고 외부로의 전류 손실 없이 캐패시턴스(c_m = 0)가 완벽하게 밀폐된 막(r_m=160)을 가지고 있다고 가정합니다.x = 0 위치에 있는 파이버에 주입된 전류는 파이버 내부를 따라 변화하지 않습니다.분사 지점에서 멀어지고 옴의 법칙(V = IR)을 사용하여 전압 변화를 다음과 같이 계산할 수 있습니다.

\displaystyle \Delta V=-i_{l}r_{l}\Delta x\}

(4)

여기서 음수는 전류가 잠재적 구배를 따라 흐르기 때문입니다.

δx를 0으로 하고 x의 증분을 무한히 작게 하면 (4)을 다음과 같이 쓸 수 있다.

{\frac V}{\partial x}=-i_{l}r_{l}\

(5)

또는

{1}{r_{l}}{\frac V}{\partial x}=-i_{l}\

(6)

r을 다시 사진에 넣는 것은_m 정원 호스에 구멍을 뚫는 것과 같습니다.구멍이 많을수록 호스에서 물이 더 빨리 빠져나가고 호스의 시작부터 끝까지 흐르는 물이 줄어듭니다.마찬가지로 축삭에서는 축삭을 통해 종방향으로 흐르는 전류의 일부가 막을 통해 빠져나갑니다.

i가 멤브레인/길이 단위(m)를 통해 유출되는 전류라면_m y단위를 따라 유출되는 총 전류는 y·i여야_m 한다.따라서 위치 x=0에서 거리 δi_l, δx에서의 축소체 내 전류 변화는 다음과 같이 나타낼 수 있다.

\displaystyle \Delta i_{l}=-i_{m}\Delta x\}

(7)

또는 무한히 작은 연속 증분을 사용하여 다음을 수행합니다.

(\displaystyle\frac i_{l}{\display x}=-i_{m}\})

(8)

$(\$ i_ ${m})$ 는 $i_{m}$ 캐패시턴스를 포함하여 다른 공식으로 표현할 수 있습니다.캐패시턴스는 세포질 측면에 있는 막을 향해 전하(전류)를 흐르게 합니다.이 전류는 보통 변위 전류(여기서 i $\$ 라고 $i_{c}$ .막의 저장 용량에 도달하지 않은 경우에만 흐름이 발생합니다. $i_{c}$ c $i_{c}$ {\ $displaystyle i_{$ c $i_{c}$ }}는 다음과 같이 나타낼 수 있습니다.

i_{c}=c_{m}{\frac {\frac V}{\partial t}}\

(9)

$c_{m}$ 서 c m $c_{m}$ { $display style$ c _ { $m$ } ${\partial V}/{\partial t}$ ${\partial V}/{\partial t}$ V / ${\$ ${\partial V}/{\partial t}$ { $style$ \ $display$ \ partial V } / { \ $partial$ t ${\partial V}/{\partial t}$ }는 ${\partial V}/{\partial t}$ 시간 경과에 따른 전압의 변화입니다.막을 통과하는 전류( $i_{r}$ \ $display i_{r$ )는 다음과 같이 나타낼 수 있습니다.

i_{r}=squalfrac {V}{r_{m}}}

(10)

$i_{m}=i_{r}+i_{c}$ m $i_{m}=i_{r}+i_{c}$ $i_{m}=i_{r}+i_{c}$ r + $i_{m}=i_{r}+i_{c}$ c { { $displaystyle$ i $_$ { m } = $i_{m}=i_{r}+i_{c}$ i _ { $r$ } + i $_$ { $c$ } $i_{m}=i_{r}+i_{c}$ 、 전극에서 전류를 더하지 않으면 i $i_{m}$ { $displaystyle i$ _ { $m}$ 에 $i_{m}$ 대한 $i_{m}$ 방정식을 도출할 수 있습니다.

{\frac i_{l}}{\frac x}=-i_{m}=-\lefts\frac {V}{r_{m}}+c_{m}{\frac {\frac V}{\partial t}}\right

(11)

${\partial i_{l}}/{\partial x}$ 서 ${\partial i_{l}}/{\partial x}$ " ${\partial i_{l}}/{\partial x}$ l / ${\partial i_{l}}/{\partial x}$ ${\partial i_{l}}/{\partial x}$ { style { $display i$ _ { $l$ } } / { \ $display$ x ${\partial i_{l}}/{\partial x}$ } where 、 종방향 전류의 단위 길이당 변화를 나타냅니다 ${\partial i_{l}}/{\partial x}$ .

식 (6)과 (11)을 조합하면 케이블 방정식의 첫 번째 버전을 얻을 수 있습니다.

{1}{r_{l}}{\frac {{2}V}{\partial x^{2}}=c_{m}{\frac {\frac V}{\partial t}}+{\frac {V}{r_{m}}}}}

(12)

2차 편미분방정식(PDE)입니다.

식 (12) (나중에 참조)의 간단한 재배열로 길이 상수 $(공간$ 상수라고도 함)와 $\tau$ 상수 $({displaystyle \lambda$ 의 두 가지 중요한 용어를 표시할 수 있습니다. 다음 섹션에서는 이러한 용어에 초점을 맞춥니다.

길이 상수

$\lambda$ 상수 $\lambda$ , \ $displaystyle$ \ $lambda$ （ $\lambda$ lambda ）는 정지 전류가 케이블의 전압에 어느 정도 영향을 미치는지를 나타내는 파라미터입니다. $\lambda$ 이 $\lambda$ 클수록 (\ $displaystyle\lambda$ 전하가 더 멀리 흐릅니다.길이 상수는 다음과 같이 나타낼 수 있습니다.

\displaystyle \displayda = displayrt {r_{m}}{r_{l}}}

(13)

막저항 r이_m 클수록 $\lambda$ (\ $displaystyle\lambda$ 의 값이 커지며, 축삭내를 종방향으로 흐르기 위해 축삭삭삭삭내를 종방향으로 흐릅니다.축색체 저항 $r_{l}$ ${\$ l $r_{l}$ 이 높을수록 $\lambda$ {\ $displaystyle \lambda$ 의 값이 작을수록 전류가 축색체를 통과하기 어려워지고 전류가 더 짧게 흐를 수 있습니다.방정식(12)을 풀고 다음 방정식에 도달할 수 있다(시간이 무한대에 가까워질 때 정상 상태 조건에서 유효하다).

({displaystyle V_{x}=V_{0}e^{-{\frac {x}{\fracda}}}}})

(14)

$V_{0}$ 서 V $V_{0}$ {\ $displaystyle$ $V_{0$ $}$ 은 $V_{0}$ x $x=0$ $x=0$ { $displaystyle$ x $=0$ }( $x=0$ 전류 주입 지점)에서의 탈분극이고 e는 지수 상수(대략값 2.71828), $V_{x}$ {\ $displaystyle V_{x}$ 는 $V_x$ x=0에서 주어진 거리에서의 전압입니다.x $=$ (\ $displaystyle$ x=\ $displayda)$ 일 $x=\lambda$ 때

{\displaystyle {x}{\displayda}}=1

(15)

그리고.

V_{x}=V_{0}e^{-1}

(16)

즉, x $x=0$ $(디스플레이 스타일$ x $=0)$ 에서 $x=0$ 거리 $\lambda$ (\ $displaystyle \displayda)$ 에서 $\lambda$ V $(\displaystyle$ V $)$ 를 $V$ $V$ 하면 다음과 같이 됩니다.

V_{\lambda}=blac {V_{0}}{e}}=0.368V_{0}

(17)

$V_{\lambda }$ V ${\$ { \ $display style$ V _ { \ $lambda }$ } $V_{0}$ $、$ $V_{0}$ 0 （ \ $display style$ V _ { $0$ } $V_{0}$ 。

시간 상수

신경과학자들은 축삭에 주입된 전류의 변화에 반응하여 축삭의 막 전위 $V_{m$ 가 얼마나 빨리 변화하는지 알아내는 데 관심이 많다. $\tau$ 상수 $\tau$ {\(\ $displaystyle\tau$ 는 해당 값에 대한 정보를 제공하는 인덱스입니다. $§$ ${\displaystyle$ \display $}$ 는 $\tau$ 다음과 같이 계산할 수 $\tau$ .

(\displaystyle \displaystyle =r_{m}c_{m}).\ }

(18)

멤브레인 캐패시턴스( $\$ 가 클수록 멤브레인 패치를 충전 및 방전하는 데 더 많은 전류가 필요하며 이 과정이 더 오래 걸립니다. $r_{m}$ $r_{m}$ m $r_{m}$ {\ $style r_{m$ 이 클수록 전류는 막전위의 변화를 유도하기 어렵다. $그러니까$ 신경 자극이 $\tau$ 높을수록 더 느리게 움직일 수 있어요즉, 막 전위(막 전체의 전압)가 전류 주입보다 더 늦습니다.응답 시간은 높은 시간 정밀도를 필요로 하는 정보를 처리하는 뉴런의 1~2밀리초에서 100밀리초 이상까지 다양합니다.일반적인 응답 시간은 약 20밀리초입니다.

일반 형식 및 수학적 구조

등호 양쪽에서 방정식(12)에 r $(\$ 을 $r_m$ 곱하면 다음과 같이 됩니다.

{r_{m}}{\frac ^{2}V}{\partial x^{2}}=c_{m}r_{m}{\frac {\partial t}+V

(19)

왼쪽의 $\lambda ^{2}={r_{m}}/{r_{l}}$ $\lambda ^{2}={r_{m}}/{r_{l}}$ $\lambda ^{2}={r_{m}}/{r_{l}}$ / $\lambda ^{2}={r_{m}}/{r_{l}}$ $\lambda ^{2}={r_{m}}/{r_{l}}$ { $displaystyle$ \ $rda$ ^ { } = { r $\lambda ^{2}={r_{m}}/{r_{l}}$ $\tau =c_{m}r_{m}$ { $m$ } / { $r$ _ { $l$ }} $\tau =c_{m}r_{m}$ and and and $= c$ _ { $m$ } $\tau =c_{m}r_{m}$ and and and = c $\tau =c_{m}r_{m}$ $r$ _ { m } 。케이블 방정식은 아마도 가장 잘 알려진 형태로 기술할 수 있습니다.

\displayda ^{2}{\frac ^{2}V}=\frac {\frac {\partial t}+V

(20)

그린의 함수, 푸리에법 등 많은 해법들이 개발되어 온 1차원 열방정식 또는 확산방정식입니다.

또한 $인덕턴스$ L(\ $displaystyle$ L $)$ 이 $L$ 사라지고 신호 전파 $1/{\sqrt {LC}}$ 1/ $1/{\sqrt {LC}}$ C $(\$ 1 $/{\sqrt {LC}})$ 가 $1/{\sqrt {LC}}$ 무한해지는 텔레그래퍼 방정식의 특수한 퇴화 사례이기도 합니다.

「」를 참조해 주세요.

레퍼런스

^ Douglas, PK; Douglas, DB (2019). "Reconsidering Spatial Priors In EEG Source Estimation : Does White Matter Contribute to EEG Rhythms?". 7th International Winter Conference on Brain-Computer Interface (BCI), Gangwon, Korea (South): 1-12. doi:10.1109/IWW-BCI.2019.8737307.

Poznanski, Roman R. (2013). Mathematical Neuroscience. San Diego [California]: Academic Press.
Tuckwell, Henry C. (1988). Introduction to theoretical neurobiology. Cambridge [Cambridgeshire]: Cambridge University Press. ISBN 978-0521350969.
de Nó, Rafael Lorente (1947). A study of nerve physiology. Studies from the Rockefeller Institute for Medical Research. Reprints. Rockefeller Institute for Medical Research. pp. Part I, 131:1-496, Part II, 132:1-548. ISBN 9780598674722. OCLC 6217290.
Lazarevich, Ivan A.; Kazantsev, Victor B. (2013). "Dendritic signal transition induced by intracellular charge in inhomogeneties". Phys. Rev. E. 88 (6): 062718. arXiv:1308.0821. Bibcode:2013PhRvE..88f2718L. doi:10.1103/PhysRevE.88.062718. PMID 24483497. S2CID 13353454.
Douglas, PK; Douglas, David B. (2019). "Reconsidering Spatial Priors In EEG Source Estimation : Does White Matter Contribute to EEG Rhythms?". 7th International Winter Conference on Brain-Computer Interface (BCI), Gangwon, Korea (South). 88: 1-12. doi:10.1109/IWW-BCI.2019.8737307.

메모들

^ 여기서 '패시브'란 막 저항이 전압에 의존하지 않는 것을 말합니다.그러나 최근 수지상 막에 대한 실험(Stuart 및 Sakmann 1994)에서는 이들 중 다수는 전압 게이트 이온 채널을 갖추고 있으므로 막 전압의 저항이 의존적이라는 것을 알 수 있습니다.따라서 대부분의 수지상 막이 수동적이지 않다는 사실을 수용하기 위해 고전적인 케이블 이론을 갱신할 필요가 있었다.
^ 기존의 케이블 이론에서는 파이버가 모델링되는 거리를 따라 일정한 반경을 갖는 것으로 가정합니다.
^ 고전적인 케이블 이론에서는 입력(일반적으로 마이크로 장치를 사용한 주입)이 선형으로 합산할 수 있는 전류라고 가정합니다.이 선형성은 시냅스막 전도율의 변화를 유지하지 못한다.

[2] Douglas, PK; Douglas, DB (2019). "Reconsidering Spatial Priors In EEG Source Estimation : Does White Matter Contribute to EEG Rhythms?". 7th International Winter Conference on Brain-Computer Interface (BCI), Gangwon, Korea (South): 1-12. doi:10.1109/IWW-BCI.2019.8737307.

[classical-1] 여기서 '패시브'란 막 저항이 전압에 의존하지 않는 것을 말합니다.그러나 최근 수지상 막에 대한 실험(Stuart 및 Sakmann 1994)에서는 이들 중 다수는 전압 게이트 이온 채널을 갖추고 있으므로 막 전압의 저항이 의존적이라는 것을 알 수 있습니다.따라서 대부분의 수지상 막이 수동적이지 않다는 사실을 수용하기 위해 고전적인 케이블 이론을 갱신할 필요가 있었다.

[fiberradius-3] 기존의 케이블 이론에서는 파이버가 모델링되는 거리를 따라 일정한 반경을 갖는 것으로 가정합니다.

[linearity-4] 고전적인 케이블 이론에서는 입력(일반적으로 마이크로 장치를 사용한 주입)이 선형으로 합산할 수 있는 전류라고 가정합니다.이 선형성은 시냅스막 전도율의 변화를 유지하지 못한다.

[a]

[1]

[b]

Search

케이블 이론

네임스페이스

더

목차

역사

케이블 방정식 도출

길이 상수

시간 상수

일반 형식 및 수학적 구조

「」를 참조해 주세요.

레퍼런스

메모들

Search

케이블 이론

역사

케이블 방정식 도출

길이 상수

시간 상수

일반 형식 및 수학적 구조

「 」를 참조해 주세요.

레퍼런스

메모들

「」를 참조해 주세요.