분류를 위한 손실 함수
Loss functions for classification| 시리즈의 일부 |
| 기계 학습 및 데이터 마이닝 |
|---|
 |
기계학습 및 수학적 최적화에서 분류를 위한 손실함수는 분류 문제(특정 관측치가 어떤 범주에 [1]속하는지 식별하는 문제)에서 예측의 부정확성에 대해 지불된 가격을 나타내는 계산적으로 실현 가능한 손실함수이다.X(으로 X {\\{} ^ { ) 및 { - { style {Y} = \ { - } \ { \ mathcal X })가 가능한 모든 입력의 공간이고 Y = { - 1 } (표준 출력의 목표치)가 주어진 ,기능 f:X→ R{\displaystyle f:{{\mathcal X}}}어느 것이 가장 좋은 주어진 입력을 위한 라벨 y{이\displaystyle}이라고 예측했다)\mathbb{R}\to →{\displaystyle{\vec{)}}}그러나 불완전한 정보, 측정에서 소음, 또는 내부 과정에서 확률론적 부품 때문에, 그것을 가능하다 .[2]. 월e x {\을(를) 생성하기 위해{\ y[3]를 사용합니다. 따라서 학습 문제의 목표는 다음과 같이 정의된 예상 손실(위험이라고도 함)을 최소화하는 것입니다.
서 V( ( ) ,) { V ( ( \ {} ) , }는 주어진 손실 함수이며 ( x,y ) { p\ \ { x} , }는 데이터를 생성한 프로세스의 확률 밀도 함수이며, 다음과 같이 쓸 수 있습니다.
분류에서 일반적으로 사용되는 몇 가지 손실 함수는 실제 y(\ y와 예측 f {\ f의 곱으로만 작성됩니다. 변수 ( x yffsilon의 함수로서 V ( x ) , ) ( ( )V ( ( \ c \ { x } ) } 、=\upsilon)는 적절히 선택된 : R {R을(를) 마진 기반 손실 함수라고 한다.마진 기반의 손실함수를 선택하는 것은 를 선택하는 것과 같으며, 이 프레임워크 내에서 손실함수를 선택하는 것은 의 }^*})에 영향을 미치므로 예상되는 위험을 최소화할 수 있습니다.
2진수 분류의 경우, 위에 명시된 적분으로부터 예상 위험의 계산을 단순화할 수 있다.구체적으로는
두 번째 등식은 위에서 설명한 속성에서 나옵니다.세 번째 등식은y(\ 에 가능한 값은 1과 -1뿐이며, 네 번째 등식은px) -p ( x) =- ( 1 \mid x )= 1 - p ( 1 \ x )이기 때문입니다.괄호안의 [ ( ) ( ) +( - ( x )] ( -p ( ) ( \ [ \ ( ∣ \ { ) + ( 1 \ { x } ) )
I[ { I [ f ] { f}에 대한 마지막 등식의 함수 도함수를 취하여 도함수를 0으로 설정하면 I [ f] { displaystyle I [ f}의 최소값을 구할 수 있다.이것은 다음과 같은 방정식을 얻을 것이다.
또한 조건부 위험의 도함수를 0으로 설정하는 것과 같다.
분류의 2진수 특성을 고려할 때, 손실 함수의 자연 선택(잘못된 긍정과 거짓 부정의 동일 비용 가정)은 0-1 손실 함수(0-1 지시 함수)가 될 것이며, 예측된 분류가 참 분류와 같으면 0을, 예측된 분류가 t와 일치하지 않으면 1을 취할 것이다.후레 클래스.이 선택 항목은 다음과 같이 모델링됩니다.
서 H H는 Heaviside 스텝 기능을 나타냅니다.단, 이 손실함수는 비볼록하고 평활하지 않으며, 최적해를 위한 해법은 NP-하드 조합 최적화 문제이다.[4]그 결과, 일반적으로 사용되는 학습 알고리즘에 다루기 쉬운 손실 함수 대용은 볼록하고 매끄러운 등의 편리한 특성을 가지므로 대체하면 좋다.계산 추적성 외에도, 이러한 손실 대용품을 사용한 학습 문제에 대한 해결책이 원래 분류 [5]문제에 대한 실제 해결책을 복구할 수 있음을 보여줄 수 있다.이들 대리체 중 일부는 아래에 설명되어 있습니다.
실제로 확률 p , pve{x},는 알 수 없습니다. 결과n개의 훈련 를 독립적으로 동일하게 분산된 샘플 포인트활용
데이터 표본 공간에서 추출하여 경험적 위험을 최소화하고자 한다.
예상되는 위험을 [3]대신할 수 있습니다.(자세한 내용은 통계학습이론을 참조해 주세요).
베이즈 일관성
Bayes의 정리를 이용하여 최적 0/ {\즉, 0-1 손실에 관련된 기대 위험을 최소화하는 f는 2진수 분류 문제에 대한 Bayes의 최적 결정 규칙을 구현하고 다음과 같은 형태를 취한다는 것을 알 수 있다.
- F 0/1∗()→)){1만약 p>안(− 1∣)→)0만약 p(1∣)→))p(− 1∣)→)− 1만약 p(1∣)→)<>안(− 1∣)→){\displaystyle f_{0/1(1∣)→)}({\vec{x}})\, =\,{\begin{경우}\.\와 같이^;1&,{\text{만약}}p(1\mid{\vec{x}})>, p(-1\mi.d{\vec{)}})(1 { {(1}})< {
손실 함수는 최적 }^{*})가 0/ ( ) δ( 인 경우 분류 등급 또는 Bayes 일관성이 있다고 한다.찬성 결정 규칙Bayes 일관성 손실 함수를 사용하면 확률 밀도 함수를 명시적으로 모델링하지 않고도 예상 위험을 직접 최소화하여 Bayes 최적 의사결정 f display display display display ( \ f _ { \ }^{ * } } }을 찾을 수 있습니다.
볼록 마진 손실 ϕ(υ){\displaystyle \phi(\upsilon)}을 예로 들자면, 만일 그것은 0에서ϕ′(0)<0{\displaystyle \phi '(0)<0}.[6][1] 하지만 구별할 수 있는 것은 ϕ(υ){\displaystyle \phi(\upsilon)}베이스 일치한다, 이 결과 비볼록형 베이스의 존재 consisten을 배제하지 않는다. 표시할 수 있다.t손실funct보다 일반적인 결과는 다음과 같은 공식을 사용하여 베이즈 일관 손실 함수를 생성할 수 있다는 것이다.
서 f ( f \1)는 f - ( -v) -f - (v ) = 1 - v ) = 1 - f^ { - 1 ( ) ( v)、 C ) 표 I는 ( C - 1 f의 일부 예에 대해 생성된 베이즈 일관 손실 함수를 보여줍니다. 새비지와 탄젠트 손실은 볼록하지 않습니다.이러한 비볼록 손실 함수는 [7][8]분류에서 특이치를 처리하는 데 유용한 것으로 나타났다.(2)에서 생성된 모든 손실 함수에 대해 후방 p x p = {{ -1( ){ 1 {{x}})= {v와 같이 반전 링크 함수를 사용하여 구할 수 있다.가역 링크를 사용하여 복구되는 것을 적절한 손실 함수라고 합니다.
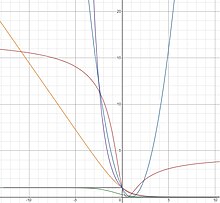
| 손실명 | ||||
|---|---|---|---|---|
| 지수 | ||||
| 로지스틱 | ||||
| 광장 | ||||
| 새비지 | ||||
| 접선 |
상기의 생성된 손실함수와 관련된 예상위험의 유일한 인 f ( \ f _ { \ * })는 식 (1)에서 직접 구할 수 있으며 하는 f \ f( \)와 동등함을 나타낼 수 있습니다.이는 비볼록 손실 함수에 대해서도 유지되며, 이는 구배 부스팅과 같은 구배 강하 기반 알고리즘을 사용하여 최소화를 구성할 수 있음을 의미한다.
적절한 손실 함수, 손실 여유 및 정규화
적절한 손실 함수의 경우 손실 여유는 µ - ( 0 ) 0) \ _ { \ - { \ { ' ( 0 ) } { \ ' ( 0 )} } 로 할 수 있으며 [9]분류기의 정규화 속성과 직접 관련이 있음을 나타냅니다.특히 마진이 큰 손실 함수는 정규화를 증가시키고 사후 확률을 더 잘 추정합니다.예를 들어, 손실액은 물류 감소를 위한 곳에서 소형 0<>1γ 로그 (1+e− γ v){\displaystyle{\frac{1}{\gamma}}\log(1+e^{-\gamma v})}는 군수 손실 쓰기를γ{\displaystyle \gamma}매개 변수 γ<>를 도입함으로써, 1{\displaystyle 0<, \gamma<1}남자를 증가 증가할 수 있다.의 rgin손실. 이는 경사 m ( ) m - () + m () ,{ (x) 의 학습 속도를 감소시키는 것과 직접 동등한 것으로 나타납니다. 여기서 를 줄이면 부스트 분류기의 정규화가 향상됩니다.이 이론은 {\\display을 사용할 때, 이제 사후 확률을 검색하는 올바른 공식은 f - ( F () \ = { - 1 ( \ F ( )) 。
결론적으로, 마진이 큰 손실 함수 표시 스타일 \를 선택함으로써 정규화를 증가시키고 사후 확률에 대한 추정치를 개선하여 최종 분류기의 ROC 곡선을 개선한다.
제곱손실
제곱 손실 함수는 회귀 분석에서 더 일반적으로 사용되지만 함수( f ( ) { ( f _ { } ) } 로 다시 작성하여 분류에 활용할 수 있다.다음과 같이 (2) 및 Table-I를 사용하여 생성할 수 있습니다.
제곱 손실 함수는 볼록하고 매끄럽습니다.그러나 제곱 손실 함수는 특이치를 과도하게 불이익시키는 경향이 있으며, 로지스틱 손실 또는 힌지 손실 [1]함수보다 (표본 복잡도와 관련하여) 수렴률이 느립니다.또한 일부 X{\fin\에 대해 f ){\vec {의 높은 값은 의 부호에 관계없이 엄중한 벌칙이 적용되므로 제곱 손실 함수의 성능이 저하됩니다.{\ y와 f ) {\이(가) 일치합니다
제곱손실함수의 장점은 그 구조가 정규화 파라미터의 간단한 교차 검증에 도움이 된다는 것입니다.특히 티코노프 정규화의 경우 단일 [10]문제를 해결하는 것과 동시에 leave-one-out cross-validation을 사용하여 정규화 파라미터를 해결할 수 있다.
제곱 손실 함수의 I[ {I [ ]의 은 다음과 같은 식 (1)에서 직접 구할 수 있습니다.
로지스틱 손실
로지스틱 손실 함수는 다음과 같이 (2) 및 표-I를 사용하여 생성할 수 있습니다.
로지스틱 손실은 볼록하며 음수 값에 대해 선형으로 증가하므로 특이치에 덜 민감합니다.로지스틱 손실은 LogitBoost 알고리즘에서 사용됩니다.
로지스틱 손실 함수의 I[ {I [ ]의 최소값은 식 (1)에서 직접 구할 수 있습니다.
이 함수는 p ) { x)=또는 p ( ) 0(각각 µ 및 쪽으로 기울어져 )일 때 정의되지p p x가 증가하고p(0)가 할 때 증가하는 부드러운 곡선을 예측합니다.5[3] 입니다.
로지스틱 손실과 바이너리 교차 엔트로피 손실(로그 손실)이 실제로 동일한지 쉽게 확인할 수 있습니다(승수 1 ( ( )\ \ { { \ log ( 2 )) 。교차 엔트로피 손실은 경험적 분포와 예측된 분포 사이의 쿨백-라이블러 분산과 밀접한 관련이 있다.교차 엔트로피 손실은 현대의 심층 신경 네트워크 어디에나 존재한다.
지수 손실
지수 손실 함수는 다음과 같이 (2) 및 표-I를 사용하여 생성할 수 있습니다.
지수 손실은 볼록하며 음수 값에 대해 지수적으로 증가하므로 특이치에 더 민감합니다.지수 손실은 AdaBoost 알고리즘에서 사용됩니다.
지수 손실 함수에 대한[ f {[ f ]의 최소치는 식 (1)에서 다음과 같이 직접 구할 수 있습니다.
새비지 손실
새비지[7] 손실은 다음과 같이 (2)와 표-I를 사용하여 생성할 수 있다.
새비지 손실은 준볼록형이며 큰 음수 값에 대해 경계가 지정되므로 특이치에 덜 민감합니다.새비지 손실은 그라데이션 부스트 및 새비지 부스트 알고리즘에 사용되어 왔습니다.
새비지 손실 함수에 대한 [f {f]의 은 식 (1)에서 다음과 같이 직접 구할 수 있습니다.
접선 손실
접선[11] 손실은 다음과 같이 (2) 및 표-I를 사용하여 생성할 수 있습니다.
탄젠트 손실은 준볼록형이며 큰 음수 값에 대해 경계가 지정되므로 특이치에 덜 민감합니다.흥미롭게도, 접선 손실은 또한 "너무 정확하게" 분류된 데이터 점에 경계 패널티를 할당합니다.이를 통해 데이터 세트에 대한 과도한 훈련을 방지할 수 있습니다.접선 손실은 그라데이션 부스트, 접선 부스트 알고리즘 및 교대 의사 결정 [12]포레스트에 사용되었습니다.
접선 손실 함수의 I[ { I의 최소값은 식 (1)에서 직접 구할 수 있습니다.
힌지 손실
손실 는 () ) (, -) )[ - + \ ( \ ) = [- \ upsilon ]_ + 로 정의됩니다서 [ + ( , )、 [ a] _ 0 . , \ ]
힌지 손실은 0-1 지시계 함수에 상대적으로 타이트하고 볼록한 상한을 제공합니다.으로, 힌지 손실은 sgn ( ( x ) ( \ \ ( fgn \ { x } ) ) (x ) {\ 1 ( \ yfc \ { x} ) \ \ 11 1 1 1 s s s s 、 、 、 、 、 、 、 、 1 risk 0 ~1、 、 、 、 、 、 、 、 、 、 벡터 머신(SVM)을 서포트합니다.서포트 벡터의 마진 경계 밖에 있는 올바르게 분류된 포인트는 패널티를 받지 않는 반면, 마진 경계 내 또는 하이퍼 플레인의 잘못된 쪽에 있는 포인트는 올바른 [4]경계로부터의 거리에 비해 선형적인 방법으로 패널티를 받는다.
힌지 손실 함수는 볼록하고 연속적이지만 y ( x ) {\}}=1}에서는 매끄럽지 않다. 따라서 힌지 손실 함수는 전체 영역에 대한 차이성에 의존하는 경사 강하 방법이나 확률적 경사 강하 방법에는 사용할 수 없다.그러나 힌지 손실은 f ) (\})=에서 하위 경사도를 가지므로 하위 경사 강하 [4]방법을 사용할 수 있습니다.힌지 손실 함수를 이용한 SVM은 2차 프로그래밍을 사용하여 해결할 수도 있습니다.
힌지 손실 기능을 위한 f \ I [ ]의 최소값은 다음과 같습니다.
x )0 0.\ p ( \ x ) \ 0.。는 0 ~1 인디케이터 함수와 일치합니다.이러한 결론은 예상 위험과 힌지 손실 [1]함수의 부호 사이의 차이에 경계가 배치될 수 있기 때문에 힌지 손실을 상당히 매력적으로 만든다. 손실은 f 힌지 {\ 이후 (2)에서 도출할 수 .힌지는 반전되지 않습니다.
일반화된 부드러운 힌지 손실
를 사용하여 일반화된 스무스 힌지 손실 함수는 다음과 같이 정의됩니다.
어디에
단조롭게 증가하며 1(\ z이면 0에 도달합니다.
「 」를 참조해 주세요.
레퍼런스
- ^ a b c d Rosasco, L.; De Vito, E. D.; Caponnetto, A.; Piana, M.; Verri, A. (2004). "Are Loss Functions All the Same?" (PDF). Neural Computation. 16 (5): 1063–1076. CiteSeerX 10.1.1.109.6786. doi:10.1162/089976604773135104. PMID 15070510. S2CID 11845688.
- ^ Shen, Yi (2005), Loss Functions For Binary Classification and Class Probability Estimation (PDF), University of Pennsylvania, retrieved 6 December 2014
- ^ a b c Rosasco, Lorenzo; Poggio, Tomaso (2014), A Regularization Tour of Machine Learning, MIT-9.520 Lectures Notes, vol. Manuscript
- ^ a b c Piyush, Rai (13 September 2011), Support Vector Machines (Contd.), Classification Loss Functions and Regularizers (PDF), Utah CS5350/6350: Machine Learning, retrieved 4 May 2021
- ^ Ramanan, Deva (27 February 2008), Lecture 14 (PDF), UCI ICS273A: Machine Learning, retrieved 6 December 2014
- ^ Bartlett, Peter L.; Jordan, Michael I.; Mcauliffe, Jon D. (2006). "Convexity, Classification, and Risk Bounds". Journal of the American Statistical Association. 101 (473): 138–156. doi:10.1198/016214505000000907. ISSN 0162-1459. JSTOR 30047445. S2CID 2833811.
- ^ a b c Masnadi-Shirazi, Hamed; Vasconcelos, Nuno (2008). "On the Design of Loss Functions for Classification: Theory, Robustness to Outliers, and SavageBoost" (PDF). Proceedings of the 21st International Conference on Neural Information Processing Systems. NIPS'08. USA: Curran Associates Inc.: 1049–1056. ISBN 9781605609492.
- ^ Leistner, C.; Saffari, A.; Roth, P. M.; Bischof, H. (September 2009). "On robustness of on-line boosting - a competitive study". 2009 IEEE 12th International Conference on Computer Vision Workshops, ICCV Workshops: 1362–1369. doi:10.1109/ICCVW.2009.5457451. ISBN 978-1-4244-4442-7. S2CID 6032045.
- ^ Vasconcelos, Nuno; Masnadi-Shirazi, Hamed (2015). "A View of Margin Losses as Regularizers of Probability Estimates". Journal of Machine Learning Research. 16 (85): 2751–2795. ISSN 1533-7928.
- ^ Rifkin, Ryan M.; Lippert, Ross A. (1 May 2007), Notes on Regularized Least Squares (PDF), MIT Computer Science and Artificial Intelligence Laboratory
- ^ Masnadi-Shirazi, H.; Mahadevan, V.; Vasconcelos, N. (June 2010). "On the design of robust classifiers for computer vision". 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition: 779–786. CiteSeerX 10.1.1.172.6416. doi:10.1109/CVPR.2010.5540136. ISBN 978-1-4244-6984-0. S2CID 632758.
- ^ Schulter, S.; Wohlhart, P.; Leistner, C.; Saffari, A.; Roth, P. M.; Bischof, H. (June 2013). "Alternating Decision Forests". 2013 IEEE Conference on Computer Vision and Pattern Recognition: 508–515. CiteSeerX 10.1.1.301.1305. doi:10.1109/CVPR.2013.72. ISBN 978-0-7695-4989-7. S2CID 6557162.



 (를) 생성하기 위해
(를) 생성하기 위해
![{\displaystyle I[f]=\displaystyle \int _{{\mathcal {X}}\times {\mathcal {Y}}}V(f({\vec {x}}),y)p({\vec {x}},y)\,d{\vec {x}}\,dy}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a681d2ec2b4e729a58045cd58dd718b1cc91b3d6)









![{\displaystyle {\begin{aligned}I[f]&=\int _{{\mathcal {X}}\times {\mathcal {Y}}}V(f({\vec {x}}),y)p({\vec {x}},y)\,d{\vec {x}}\,dy\\[6pt]&=\int _{\mathcal {X}}\int _{\mathcal {Y}}\phi (yf({\vec {x}}))p(y\mid {\vec {x}})p({\vec {x}})\,dy\,d{\vec {x}}\\[6pt]&=\int _{\mathcal {X}}[\phi (f({\vec {x}}))p(1\mid {\vec {x}})+\phi (-f({\vec {x}}))p(-1\mid {\vec {x}})]p({\vec {x}})\,d{\vec {x}}\\[6pt]&=\int _{\mathcal {X}}[\phi (f({\vec {x}}))p(1\mid {\vec {x}})+\phi (-f({\vec {x}}))(1-p(1\mid {\vec {x}}))]p({\vec {x}})\,d{\vec {x}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b790a75d49d31c4d0b845445046bae07114894ee)

 대한 마지막 등식의 함수 도함수를 취하여 도함수를 0으로 설정하면 I [ f
대한 마지막 등식의 함수 도함수를 취하여 도함수를 0으로 설정하면 I [ f![I[f]](https://wikimedia.org/api/rest_v1/media/math/render/svg/8213b3ec4b7c34969992d3f12dd96b830c9082ef) 최소값을 구할 수 있다.이것은 다음과 같은 방정식을 얻을 것이다.
최소값을 구할 수 있다.이것은 다음과 같은 방정식을 얻을 것이다.


 동일
동일
![{\displaystyle I_{S}[f]={\frac {1}{n}}\sum _{i=1}^{n}V(f({\vec {x}}_{i}),y_{i})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f11407df44b1dc610c3fe193ce436cc33520ffe5)


![{\displaystyle \phi (v)=C[f^{-1}(v)]+(1-f^{-1}(v))C'[f^{-1}(v)]\;\;\;\;\;(2)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ba1d9d0d51b1c65272af55aa780a285afa90d9d)
 f
f











![{\displaystyle {\frac {1}{\log(2)}}[-\eta \log(\eta )-(1-\eta )\log(1-\eta )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e609e1c16646f7a8a99eb51b64fb94416a6a425)














 수 있으며
수 있으며 
 줄이면 부스트 분류기의 정규화가 향상됩니다.이 이론은
줄이면 부스트 분류기의 정규화가 향상됩니다.이 이론은 

![{\displaystyle \phi (v)=C[f^{-1}(v)]+(1-f^{-1}(v))C'[f^{-1}(v)]=4({\frac {1}{2}}(v+1))(1-{\frac {1}{2}}(v+1))+(1-{\frac {1}{2}}(v+1))(4-8({\frac {1}{2}}(v+1)))=(1-v)^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7cdde8f62987c985c1028a98d8c24682dfe0c2d7)

 높은 값은
높은 값은 
![{\displaystyle {\begin{aligned}\phi (v)&=C[f^{-1}(v)]+\left(1-f^{-1}(v)\right)\,C'\left[f^{-1}(v)\right]\\&={\frac {1}{\log(2)}}\left[{\frac {-e^{v}}{1+e^{v}}}\log {\frac {e^{v}}{1+e^{v}}}-\left(1-{\frac {e^{v}}{1+e^{v}}}\right)\log \left(1-{\frac {e^{v}}{1+e^{v}}}\right)\right]+\left(1-{\frac {e^{v}}{1+e^{v}}}\right)\left[{\frac {-1}{\log(2)}}\log \left({\frac {\frac {e^{v}}{1+e^{v}}}{1-{\frac {e^{v}}{1+e^{v}}}}}\right)\right]\\&={\frac {1}{\log(2)}}\log(1+e^{-v}).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fd7a4c1188c935bcf5f76e4063f97034fb54e39)



 증가하고
증가하고

![{\displaystyle \phi (v)=C[f^{-1}(v)]+(1-f^{-1}(v))C'[f^{-1}(v)]=2{\sqrt {({\frac {e^{2v}}{1+e^{2v}}})(1-{\frac {e^{2v}}{1+e^{2v}}})}}+(1-{\frac {e^{2v}}{1+e^{2v}}})({\frac {1-{\frac {2e^{2v}}{1+e^{2v}}}}{\sqrt {{\frac {e^{2v}}{1+e^{2v}}}(1-{\frac {e^{2v}}{1+e^{2v}}})}}})=e^{-v}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aaf52f9ceb280f470317e416a711b1e924cc1bd0)

![{\displaystyle \phi (v)=C[f^{-1}(v)]+(1-f^{-1}(v))C'[f^{-1}(v)]=({\frac {e^{v}}{1+e^{v}}})(1-{\frac {e^{v}}{1+e^{v}}})+(1-{\frac {e^{v}}{1+e^{v}}})(1-{\frac {2e^{v}}{1+e^{v}}})={\frac {1}{(1+e^{v})^{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bc29f01f367ef3f4d6f92ce2f91827622a59b30)

![{\displaystyle {\begin{aligned}\phi (v)&=C[f^{-1}(v)]+(1-f^{-1}(v))C'[f^{-1}(v)]=4(\arctan(v)+{\frac {1}{2}})(1-(\arctan(v)+{\frac {1}{2}}))+(1-(\arctan(v)+{\frac {1}{2}}))(4-8(\arctan(v)+{\frac {1}{2}}))\\&=(2\arctan(v)-1)^{2}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48fc53108e779ecf1e26b0725b3873944fcd9644)

![{\displaystyle \phi (\upsilon )=\max(0,1-\upsilon )=[1-\upsilon ]_{+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/068b33990cb9f189f89c1c4b775424ff8bd5fade)
![{\displaystyle V(f({\vec {x}}),y)=\max(0,1-yf({\vec {x}}))=[1-yf({\vec {x}})]_{+}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bec5bd9d55a0fa201d877181b995db28b17f9827)




 반전되지 않습니다.
반전되지 않습니다.  사용하여 일반화된 스무스 힌지 손실 함수는 다음과 같이 정의됩니다.
사용하여 일반화된 스무스 힌지 손실 함수는 다음과 같이 정의됩니다.




