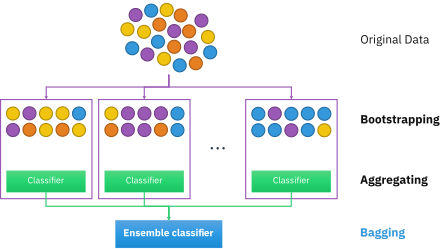
부트스트랩 집약

시리즈의 일부
기계 학습 및 데이터 마이닝
문제 분류 클러스터링 회귀 이상 검출 데이터 클리닝 자동 ML 어소시에이션 규칙 강화 학습 구조화된 예측 기능 엔지니어링 기능 학습 온라인 학습 준지도 학습 비지도 학습 순위 매기기 학습 문법 유도
지도 학습 (분류 • 회귀) 의사결정 트리 앙상블 배깅 부스팅 랜덤 포레스트 k-NN 선형 회귀 네이비 베이즈 인공신경망 로지스틱 회귀 분석 퍼셉트론 관련 벡터 머신(RVM) 서포트 벡터 머신(SVM)
클러스터링 버치 치유하다 계층적 k자형 기대 최대화(EM) DBSCAN 광학 평균 이동
치수 축소 인자 분석 CCA ICA LDA NMF PCA PGD t-SNE
구조화된 예측 그래픽 모델 베이즈 네트 조건부 랜덤 필드 히든 마르코프
이상 검출 k-NN 국소 특이치 계수
인공신경망 자동 인코더 인지 컴퓨팅 딥 러닝 딥 드림 다층 퍼셉트론 RNN LSTM GRU ESN 저장고 계산 제한 볼츠만 기계 GAN somerset. 컨볼루션 뉴럴 네트워크 유넷 트랜스포머 비전. 스파이킹 뉴럴 네트워크 메모리 트랜지스터 전기화학 RAM(ECRAM)
강화 학습 Q-러닝 사사 시간차(TD) 멀티 에이전트 셀프 플레이
인간과의 학습 액티브 러닝 크라우드 소싱 휴먼 인 더 루프
모델 진단 학습 곡선
이론. 커널 머신 바이어스-분산 트레이드오프 컴퓨터 학습 이론 경험적 리스크 최소화 오컴 러닝 PAC 학습 통계학 학습 VC 이론
기계학습장 NeurolIPS ICML ML JMLR ArXiv:cs.LG
관련 기사 인공지능 용어집 기계 학습 연구를 위한 데이터 세트 목록 기계학습의 개요
v t

부트스트랩 애그리게이션은 (부트스트랩 애그리게이션에서) 배깅이라고도 불리며 통계 분류 및 회귀에 사용되는 머신러닝 알고리즘의 안정성과 정확성을 향상시키기 위해 설계된 머신러닝 앙상블 메타 알고리즘입니다.또한 분산을 줄이고 과적합을 방지하는 데 도움이 됩니다.일반적으로 Decision Tree 메서드에 적용되지만 모든 유형의 메서드에 사용할 수 있습니다.배깅은 모델 평균화 접근법의 특별한 경우입니다.

기술 설명

크기 n의 표준 $트레이닝$ $세트{\displaystyle }$D {\$displaystyle$ $D}$가 주어졌을 때, 배깅은 D에서 균일하게 샘플링하여 치환하여 각각 크기 n†의 새로운 트레이닝 $세트{\displaystyle {}_{}}$ ${\displaystyle {Di}_{}}${{$i$를 생성합니다.치환 표본 추출을 통해 각 $(\$에서 일부 관측치를 반복할 수 있으며, n==n일 경우 ${\displaystyle {집합}_{}}$Di(\$displaystyle D_{$i$$})는 D의 고유 예 중 부분(1 - 1/e)(1,063.2%)^[1]을 가질 것으로 예상된다.이런 종류의 샘플은 부트스트랩 샘플이라고 불립니다.교환을 사용한 샘플링은 샘플링 시 이전에 선택한 샘플에 의존하지 않기 때문에 각 부트스트랩은 피어로부터 독립적입니다.그런 다음 위의 m개의 부트스트랩 샘플을 사용하여 m개의 모델을 적합시키고 출력의 평균화(회귀용) 또는 투표(분류용)를 통해 결합합니다.

배깅은 "불안한 절차를 위한 개선"^[2]으로 이어지며, 여기에는 예를 들어 인공 신경 네트워크, 분류 및 회귀 트리, 선형 ^[3]회귀에서의 부분 집합 선택 등이 포함된다.배깅은 초기 이미지 ^[4][5]학습을 개선하는 것으로 나타났다.한편, K-근접 ^[2]이웃과 같은 안정적인 방법의 성능을 약간 저하시킬 수 있습니다.

알고리즘 프로세스

주요 용어

부트스트랩 애그리게이션에는 세 가지 유형의 데이터 세트가 있습니다.이러한 데이터 세트는 원래 데이터 세트, 부트스트랩 데이터 세트 및 기본 데이터 세트입니다.아래의 각 섹션에서는 원본 데이터 집합을 제외한 각 데이터 집합의 작성 방법에 대해 설명합니다.원래 데이터 세트는 제공된 모든 정보입니다.

부트스트랩 데이터 세트 생성

부트스트랩 데이터 집합은 원래 데이터 집합에서 개체를 임의로 선택하여 만들어집니다.또한 원래 데이터 집합과 크기가 같아야 합니다.그러나 차이점은 부트스트랩 데이터 세트에 중복된 개체가 있을 수 있다는 것입니다.아래 그림과 함께 동작하는 간단한 예를 제시하겠습니다.

원래 데이터 집합이 12명으로 구성된 그룹이라고 가정합니다.이 사람들은 에밀리, 제시, 조지, 콘스탄틴, 렉시, 테오도르, 존, 제임스, 레이첼, 앤서니, 엘리, 자말이야.

이름 그룹을 무작위로 선택하여 부트스트랩 데이터 세트에 James, Elli, Constantine, Lexi, John, Constantine, Todore, Constantine, Anthony, Lexi, Constantine 및 Todore가 포함되었다고 가정해 보겠습니다.이 경우 부트스트랩 샘플에는 Constantine의 경우 4개, Lexi와 Todore의 경우 2개의 중복이 포함되어 있습니다.

즉시 사용 가능한 데이터 세트 생성

아웃오브백 데이터 세트는 부트스트랩 데이터 세트에 포함되지 않은 나머지 사용자를 나타냅니다.원본 데이터 세트와 부트스트랩 데이터 세트 간의 차이를 취하여 계산할 수 있습니다.이 경우 선택되지 않은 나머지 샘플은 Emily, Jessie, George, Rachel 및 Jamal입니다.두 데이터셋은 모두 세트이기 때문에 차이를 취할 때 부트스트랩 데이터셋에서 중복 이름은 무시됩니다.아래 그림은 계산 방법을 보여 줍니다.

중요성

부트스트랩 및 아웃오브백 데이터셋은 랜덤 포레스트 알고리즘의 정확성을 테스트하는 데 사용되므로 작성은 매우 중요합니다.예를 들어 부트스트랩/아웃오브백 데이터셋을 사용하여 50개의 트리를 생성하는 모델은 10개의 트리를 생성하는 경우보다 정확도가 더 높습니다.알고리즘은 여러 트리를 생성하므로 여러 데이터셋을 생성하므로 부트스트랩 데이터셋에서 개체가 제외될 가능성은 낮습니다.다음 몇 가지 섹션에서는 랜덤 포레스트 알고리즘의 동작에 대해 자세히 설명합니다.

Decision Tree 생성

알고리즘의 다음 단계에서는 부트스트랩된 데이터셋에서 의사결정 트리를 생성합니다.이를 달성하기 위해 각 유전자/특징을 검사하고 해당 특성의 유무에 따라 얼마나 많은 샘플이 양성 또는 음성 결과를 산출하는지 결정합니다.그런 다음 이 정보를 사용하여 분류자로 사용할 때 기능의 참 긍정, 거짓 긍정, 참 부정 및 거짓 부정을 나열하는 혼동 매트릭스를 계산합니다.그런 다음 이러한 특징들은 혼란 매트릭스에 기초하여 다양한 분류 지표에 따라 순위가 매겨진다.몇 가지 일반적인 지표에는 양의 정확성 추정치(진정한 양의 양에서 잘못된 양의 값을 뺀 값으로 계산), "선도" 측정치 및 정보 이득이 포함됩니다.그런 다음 이러한 기능을 사용하여 샘플을 상위 기능을 가진 세트와 그렇지 않은 세트로 분할합니다.

아래 다이어그램은 데이터 분류에 사용되는 깊이 2의 Decision Tree를 보여 줍니다.예를 들어 기능 1을 표시하지만 기능 2를 표시하지 않는 데이터 점에는 "아니오"가 지정됩니다.특징 1을 나타내지 않지만 특징 3을 나타내는 다른 점에는 "예"가 부여됩니다.

이 프로세스는 원하는 깊이에 도달할 때까지 트리의 연속적인 레벨에 대해 반복됩니다.트리의 맨 아래에서 최종 피쳐에 대해 양성으로 테스트한 샘플은 일반적으로 양성으로 분류되고 기능이 없는 샘플은 ^[6]음성으로 분류됩니다.그런 다음 이 트리는 새 데이터를 분류하기 위한 예측 변수로 사용됩니다.

랜덤 포레스트

알고리즘의 다음 부분에서는 부트스트랩된 트리에 또 다른 가변 요소를 도입합니다.각 트리는 부트스트랩된 샘플세트만 검사할 뿐만 아니라 분류자로 순위를 매길 때는 작지만 일관된 수의 고유 기능만 고려됩니다.즉, 각 트리는 적은 수의 기능 및 원래 데이터 집합보다 작거나 같은 수의 가변 샘플과 관련된 데이터만 알고 있습니다.결과적으로, 나무들은 보다 다양한 지식에서 파생된 광범위한 답을 반환할 가능성이 더 높습니다.이것은 무작위 포레스트를 낳으며, 무작위 없이 생성된 단일 의사결정 트리에 비해 많은 이점을 가진다.랜덤 포레스트에서는 각 트리가 특징에 따라 샘플을 양성으로 분류할지 여부를 "투표"합니다.샘플은 다수결로 분류된다.이에 대한 예는 아래 다이어그램에 제시되어 있으며, 랜덤 포레스트의 4그루는 돌연변이 A, B, F, G를 가진 환자의 암 여부를 투표한다.나무 4그루 중 3그루가 찬성표를 던지기 때문에 환자는 암 양성으로 분류된다.

랜덤 포레스트는 속성상 가장 정확한 데이터 마이닝 알고리즘 중 하나로 간주되며, 데이터 오버핏 가능성이 낮으며, 대규모 ^[7]데이터셋에서도 빠르고 효율적으로 실행됩니다.데이터 집합에서 통계 변수 간에 관측된 연결을 그리려는 회귀 분석과는 달리, 주로 분류에 유용합니다.따라서 랜덤 포레스트는 은행, 의료, 주식시장 및 전자상거래와 같은 분야에서 특히 유용합니다.이 분야에서는 과거의 ^[8]데이터를 바탕으로 미래의 결과를 예측할 수 있는 것이 중요합니다.이들의 응용 프로그램 중 하나는 위의 예에서 보듯이 유전적 요인에 기초한 암을 예측하는 데 유용한 도구가 될 것이다.

랜덤 포레스트를 설계할 때 고려해야 할 몇 가지 중요한 요소가 있습니다.랜덤 포레스트의 트리가 너무 깊으면 과특성으로 인해 과적합이 발생할 수 있습니다.포리스트가 너무 크면 런타임 증가로 인해 알고리즘의 효율성이 저하될 수 있습니다.랜덤 포레스트는 변동성이 ^[8]거의 없는 희박한 데이터가 주어지면 일반적으로 성능이 좋지 않습니다.그러나 해석하기가 훨씬 쉽고 일반적으로 ^[9]훈련에 필요한 데이터가 적기 때문에 뉴럴 네트워크와 같은 유사한 데이터 분류 알고리즘에 비해 여전히 많은 이점이 있다.랜덤 포레스트의 필수 컴포넌트로서 부트스트랩 애그리게이션은 알고리즘 분류에 매우 중요하며, 아래에 설명한 바와 같이 새로운 데이터를 분석할 때 정확성을 높일 수 있는 가변성의 중요한 요소를 제공합니다.

군중의 지혜

정확한 의사결정 트리와 랜덤 포레스트를 생성하는 데 중요한 요소 중 하나는 군중의 지혜를 활용하는 것입니다.군중의 지혜는 ^[10]한 사람의 전문가의 의견이라기보다는 개인의 집단적 의견이다.군중의 지혜를 활용하면 다중 의사결정 나무에서 개발된 랜덤 포레스트를 정확하게 할 수 있다.랜덤 포레스트를 구축할 때 각 Decision Tree는 군중 속에서 한 사람 역할을 합니다.하나의 의사결정 트리의 결과는 랜덤 포레스트를 생성할 때 다음 결과물에 의존하지 않으며, 그것들은 돌연변이 및 샘플 공유 집합에서 랜덤화된 데이터의 서브셋으로 독립적으로 생성된다.생성된 각 트리가 투표를 결정하고 이러한 결과의 평균을 구하면 군중의 지혜에 따라 결과가 결정됩니다.

이 방법을 효과적으로 구현하기 위해 군중(의사결정 트리)은 아래 표에 열거된 전제조건 특성을 포함해야 한다.

현명한[11] 군중에게 필요한 5가지 자질 기준 개요 랜덤 포레스트 접속 의견의 다양성 알려진 사실에 대한 괴이한 해석일지라도 개인정보는 있어야 한다. 돌연변이와 샘플은 포레스트의 각 트리가 공유하는 알려진 데이터입니다.각 트리에 의해 개발된 투표는 모든 의사결정 트리 결과가 집계될 때까지 "개인" 정보이다.공유 데이터의 무작위화된 하위 집합도 "개인"입니다." 인디펜던스 사람들의 의견은 주변 사람들의 의견으로 결정되는 것이 아니다. 구축되는 각 의사결정 트리는 임의로 선택된 자체 데이터 서브셋과 독립적입니다.각 트리의 이 랜덤화된 부분 집합은 다른 트리의 부분 집합의 영향을 받지 않습니다. 분산화 사람들은 자신의 지역 지식을 전문화하고 활용할 수 있다. 의사결정 트리는 다른 의사결정 트리의 결과에 기초하여 결과를 형성하는 대신, 정확한 결과를 결정하기 위해 특정 데이터 세트의 결과를 이용한다. 집약 사적 판단을 집단적 결정으로 바꾸기 위한 몇 가지 메커니즘이 존재한다. 각 트리는 자체 결과를 반환하며, 이를 통해 각 트리의 집합 결과를 최종 결과와 비교할 수 있습니다. 신뢰 각 개인은 집단 집단이 공정하고 유효하다고 신뢰합니다. 랜덤 포레스트에 대한 신뢰는 각 의사결정 트리가 생성되고 각 개별 결과가 단독으로 정확하며, 집합 그룹으로서 모든 결과의 집계가 정확하다는 믿음을 의미한다. **이 표는 Wise Crowd가 있는 랜덤 포레스트를 생성하기 위해 필요한 5가지 기준을 정의합니다.**

위의 기준을 충족했을 때 군중의 지혜는 현명한 판단을 낳는다.그러나 군중의 지혜가 정확하지 않아 판단 실패가 발생하는 경우가 있다.판단 실패의 원인이 되는 군중의 예로는 폭도, 시장 붕괴를 경험한 시민 등이 있습니다.군중의 지혜는 의사결정 트리 생성에 유용할 뿐만 아니라 마케팅, 소셜 데이터 분석 생성 등에 활용될 수 있다.무작위 숲에서 군중의 지혜를 생성하고 연구하는 것은 전체적인 결정 결과를 판단하는 정확한 방법입니다.다음은 주어진 랜덤 포레스트 생성에서 군중의 지혜가 어떻게 기능하는지를 보여주는 간단한 예입니다.

이 예에서는 여름인지 아닌지가 판정되어야 합니다.이것은 한 달 동안의 온도 데이터 세트입니다. [76, 82, 69, 67, 87, 70, 66, 42, 48, 51, 65, 74, 88, 90, 59, 67, 49, 52, 67, 63, 64, 67, 77, 75, 65, 55, 91].이것은 각 의사결정 트리에 대해 12온도의 서브셋을 만드는 데 사용되는 데이터 세트입니다.이 예에서는 3개의 생성된 트리(3개의 랜덤화된 온도 서브셋)가 있습니다.다음 그림은 Decision Tree 1의 서브셋과 트리가 어떻게 결정을 내리고 결과를 도출하는지에 대한 설명을 보여줍니다.

Decision Tree 1의 Decisions 라벨이 붙은 그림

트리 1의 온도 77은 Decision 1에 대해 Yes(네)로 응답하고 왼쪽 Decision 2로 이동합니다.그런 다음 Decision 2에서도 yes라고 대답하고 트리의 가장 왼쪽에 있는 분기로 이동합니다.이는 서브셋에서 각 온도를 사용하여 다른 2개의 의사결정 트리(사람)를 구축하는 데 사용되는 프로세스와 동일합니다.이 예에서는 생성된 3개의 트리가 군중 역할을 합니다.Tree 1은 위와 같이 여름인지 아닌지에 대한 투표 "Yes"를 반환했으며, 이 결정을 평가한 서브셋의 데이터 대부분이 "Yes"로 나타났다.이 군중들의 결과는 아래 이미지에 나와 있습니다.녹색은 각 서브셋의 "Yes" 온도를 나타내고 분홍색은 각 결정 기준에 따른 "No" 온도를 나타냅니다.

최종 Decision Tree 결과:

위의 예에서 각 트리(사람)에서 생성된 표를 보면 트리 1과 트리 2에서 여름으로 투표되었습니다.트리 3에서는, 「아니오」라고 합니다.각 트리의 결과를 집계하면 여름의 경우 대부분 3번 중 2번 "Yes"가 반환됩니다.이 예에서 군중은 전체 결과가 yes임을 나타냅니다.이것은 랜덤 포레스트가 사실상 여름이라는 최종 결과를 낳았다는 것을 의미합니다.

이 간단한 예는 각 의사결정 트리 결과의 집계가 어떻게 군중의 지혜에 기초한 하나의 최종 결정으로 이어지는지를 보여준다.각 Decision Tree의 구축 방법은 표에 설정된 기준을 따릅니다.

군중의 지혜를 활용하면 다양한 데이터가 생성됩니다.이것이 랜덤 포레스트를 매우 정확하게 할 수 있게 하는 것입니다.이 섹션에서 설명하는 기준을 따르지 않으면 생성된 랜덤 포레스트를 신뢰하여 모든 종류의 데이터를 정확하게 결정할 수 없습니다.이는 의사결정 나무와 랜덤 포레스트를 사용하여 데이터를 생성하고 평가할 때 고려해야 할 가장 중요한 측면 중 하나이다.다음 섹션에서는 군중들의 지혜와 더불어 특징을 가진 랜덤 포레스트를 개선하는 방법을 다룰 것이다.

랜덤 포레스트 및 배지 개선

위에서 설명한 랜덤 포레스트, 배깅(부트스트래핑) 및 군중들의 지혜는 그 자체로 매우 유용하지만, 그 실행 및 투표 시간, 예측 정확도 및 전체적인 성능을 향상시키기 위해 사용할 수 있는 몇 가지 방법이 있습니다.다음은 효율적인 랜덤 포레스트를 작성하기 위한 주요 단계입니다.

1. 트리의 최대 깊이를 지정합니다.모든 노드가 순수해질 때까지 랜덤 포리스트를 계속하는 대신 특정 시점에서 포리스트를 잘라 과적합 가능성을 더욱 줄이는 것이 좋습니다.
2. 데이터 집합을 제거합니다.매우 큰 데이터 세트를 사용하면 초점을 맞추고 있는 대상을 보다 정확하게 나타내는 작은 데이터 세트보다 제공된 데이터를 덜 나타내는 결과를 만들 수 있습니다.
   • 원래 배깅 프로세스뿐만 아니라 각 노드 분할 시에도 데이터를 플루닝합니다.
3. 정확도 또는 속도 결정:원하는 결과에 따라 포레스트 내의 트리 수를 늘리거나 줄이는 것이 도움이 됩니다.일반적으로 나무 수를 늘리면 더 정확한 결과를 얻을 수 있고, 나무 수를 줄이면 더 빠른 결과를 얻을 수 있습니다.

랜덤 포레스트와 백깅의 장단점

장점	단점
정규화와 확장에 관련된 요건이 전반적으로 적기 때문에 랜덤 포레스트 사용이 더욱 [12]편리해집니다.	포레스트 내에서 [13]부트스트랩되어 사용되는 데이터에 약간의 변경이 있을 경우 알고리즘이 크게 변경될 수 있습니다.즉, 랜덤 포레스트는 데이터 세트에 매우 의존합니다.데이터 세트를 변경하면 각 나무의 구조가 크게 바뀔 수 있습니다.
간단한 데이터 준비.데이터는 부트스트랩세트와 일정 수의 Decision Tree를 생성하여 랜덤포레스트를 구축함으로써 준비됩니다(Random Forest 섹션 참조).	랜덤 포레스트는 단독 의사결정 트리나 다른 알고리즘보다 구현이 복잡합니다.이는 포레스트 전체를 생성하기 위해 재귀의 필요성뿐만 아니라 백잉을 위한 추가 단계를 밟기 때문에 구현이 복잡하기 때문입니다.이 때문에 계산 능력과 계산 자원을 훨씬 더 많이 필요로 합니다.
다중 의사결정 트리로 구성된 숲은 보다 정확하게 예측을 할 수 있다.군중의 지혜를 바탕으로 예측을 하는 것이 훨씬 정확하다.예를 들어, 한 사람이 대통령에게 투표하도록 하는 것은 모든 사람들이 투표하도록 하는 것보다 여론의 진실을 덜 정확하게 묘사한다.	Decision Tree에 비해 데이터를 트레이닝하는 데 시간이 많이 소요됩니다.각 트리가 더 작은 샘플과 기능을 사용하더라도 훨씬 더 많은 데이터를 전송해야 하기 때문에 큰 포레스트를 갖는 것은 프로그램 작동 속도를 빠르게 감소시키기 시작할 수 있습니다.
비선형 데이터에 적합합니다.비선형 데이터는 단일 수준을 포함하지 않는 데이터이므로 한 번에 통과할 수 없습니다.단일 의사 결정 트리와 같은 다른 데이터 마이닝 기술도 이를 처리하지 못하기 때문에 비선형 데이터를 잘 사용하면 큰 이점이 있습니다.	랜덤 포레스트 분류기 내에서 결정을 내리고 투표하는 데 훨씬 더 많은 시간이 필요합니다.랜덤 포레스트 분류자는 군중의 지혜를 이용해 투표해야 하며, 이는 단일 의사결정 트리 내에서 분류하는 것보다 훨씬 많은 시간이 소요됩니다.
과적합 위험이 낮아 대규모 데이터 [14]세트에서도 효율적으로 실행됩니다.이는 랜덤 포레스트가 랜덤피처 선택과 함께 배깅을 사용한 결과입니다.	교육 데이터의 범위를 벗어나는 예측은 하지 않습니다.이는 백깅이 효과적인 경우가 많지만 모든 데이터가 고려되지 않기 때문에 전체 데이터 집합을 예측할 수 없기 때문입니다.
랜덤 포레스트 분류기는 높은 정확도와 [15]속도로 작동합니다.랜덤 포레스트는 데이터 세트가 작기 때문에 의사 결정 트리보다 훨씬 빠릅니다.	특정 결과를 재생성하려면 부트스트랩세트 생성에 사용된 정확한 랜덤시드를 추적해야 합니다.이는 연구를 위해 또는 데이터 마이닝 클래스 내에서 데이터를 수집할 때 중요할 수 있습니다.랜덤 시드를 사용하는 것은 랜덤 포레스트에 필수적이지만 시드를 기록하지 못한 경우 포레스트에 기반한 스테이트먼트를 지원하는 것이 어려워질 수 있습니다.
특이치가 많은 결측 데이터 및 데이터 집합을 잘 처리합니다.이들은 이 문제를 바이닝을 사용하거나 값이 크게 다른 것을 피하기 위해 값을 그룹화하여 해결합니다.

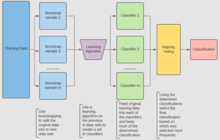
알고리즘(분류)

분류에는 트레이닝 $세트{\displaystyle }$D(\$displaystyle$ D$),$ $Inducer{\displaystyle }$ I$(\displaystyle$ I$)$ 및$$ 부트스트랩 $샘플{\displaystyle }$ 수$$m(\$displaystyle$ m$)$을 사용합니다.$분류자$ C ${\$ {\$style$C^{*}}를$$ 출력으로 생성합니다^[16].

1. $D에서$새 트레이닝 세트${\displaystyle {}_{}}$$$$($$Displaystyle$$D_{i$를 작성합니다$$(교체를 포함).
2. $분류자{\displaystyle {}_{}}$ $(\$})는$$ I$(\displaystyle$ I$)$를 $사용$하여 각 $세트{\displaystyle {}_{}}$ $(\$})에서$$ 구축되어 $세트{\displaystyle {}_{}}$ $(\$})의 분류를 결정합니다.
3. 마지막으로 $분류자{\displaystyle {}^{}}$ C ${\$ {\$displaystyle$ C$^{*}$는 원본 데이터$$ $세트{\displaystyle }$D {\$displaystyle$ D$\}$에서 이전에 생성된 $분류자{\displaystyle {}_{}}$ ${\displaystyle {Ci}_{}}${\$displaystyle C_{i$}를$$ 사용하여 생성되며, 하위 $분류자{\displaystyle {}_{}}$ ${\displaystyle {Ci}_{}}${$displaystyle C_{i$}에$$ 의해 가장 자주 예측되는 분류가 최종 분류가 됩니다.

i = 1 ~ m { D' = D의 부트스트랩 샘플(교체 샘플 포함) Ci = I(D') } C*(x) = argmax #{i:Ci(x)=y}(가장 자주 예측 레이블 y) y440Y

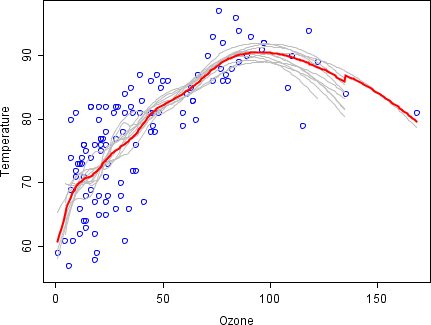
예: 오존 데이터

배깅의 기본 원리를 설명하기 위해, 아래는 오존과 온도 사이의 관계에 대한 분석이다(Rouseeu와 Leroy^{[clarification needed]}(1986)의 데이터, R로 분석).

이 데이터 집합에서 온도와 오존 사이의 관계는 산란도를 기준으로 비선형인 것으로 보입니다.이 관계를 수학적으로 설명하기 위해 LOESS 스무더(대역폭 0.5)를 사용합니다.전체 데이터 세트에 대해 단일 평활기를 구축하는 대신 100개의 부트스트랩 샘플을 추출했습니다.각 표본은 원래 데이터의 랜덤 부분 집합으로 구성되며 마스터 집합의 분포와 변동성의 외관을 유지합니다.각 부트스트랩 샘플에 대해 LOESS 스무더가 장착되었습니다.그런 다음 이 100개의 평활기에서 데이터 범위에 걸쳐 예측을 수행했습니다.검은색 선은 이러한 초기 예측을 나타냅니다.이 선들은 예측에 일관성이 없고 데이터 점을 지나치게 적합시키는 경향이 있습니다. 이는 선들의 흔들리는 흐름을 보면 알 수 있습니다.

각각 원래 데이터 세트의 하위 집합에 해당하는 평활기 100개의 평균을 취하면 하나의 봉지화된 예측 변수(빨간색 선)에 도달합니다.빨간색 선의 흐름은 안정적이며 데이터 포인트에 지나치게 부합하지 않습니다.

장점과 단점

장점:

• 집계된 많은 약한 학습자는 일반적으로 전체 집합에서 한 학습자보다 성능이 우수하며, 오버핏이 적습니다.
• 고분산 저편중 저편중 취약 학습자의 편차를 제거한다.
• 각 부트스트랩을 조합하기^[18] 전에 단독으로 처리할 수 있으므로 병렬로 실행할 수 있습니다.

단점:

• 높은 편향을 가진 약한 학습자의 경우, 배깅은 또한 높은^[17] 편향을 골재에 전달합니다.
• 모형의 해석 가능성 손실.
• 데이터 세트에 따라 계산 비용이 많이 들 수 있습니다.

역사

부트스트랩 집약의 개념은 Bradley Efron에 ^[19]의해 개발된 부트스트랩의 개념에서 파생되었습니다.부트스트랩 애그리게이팅은 Leo Breiman에 의해 제안되었으며, Leo Breiman은 또한 "bagging"(부트스트랩 애그리게이션)이라는 약어를 만들었습니다.Breiman은 1994년에 무작위로 생성된 훈련 세트의 분류를 결합하여 분류를 개선하기 위해 배깅 개념을 개발했습니다.그는 "학습 세트를 교란시키는 것이 구성된 예측 변수에 상당한 변화를 일으킬 수 있다면, 배깅은 정확도를 향상시킬 수 있다"^[3]고 주장했다.

「 」를 참조해 주세요.

• 부스트(메타 알고리즘)
• 부트스트랩(통계정보)
• 교차 검증(통계)
• 아웃오브백에러
• 랜덤 포레스트
• 랜덤 서브스페이스 방식(속성 배깅)
• 효율적인 프런티어 재샘플링
• 예측 분석:분류 및 회귀 트리

레퍼런스

추가 정보

• Breiman, Leo (1996). "Bagging predictors". Machine Learning. 24 (2): 123–140. CiteSeerX 10.1.1.32.9399. doi:10.1007/BF00058655. S2CID 47328136.
• Alfaro, E., Gámez, M. and García, N. (2012). "adabag: An R package for classification with AdaBoost.M1, AdaBoost-SAMME and Bagging". {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)
• Kotsiantis, Sotiris (2014). "Bagging and boosting variants for handling classifications problems: a survey". Knowledge Eng. Review. 29 (1): 78–100. doi:10.1017/S0269888913000313. S2CID 27301684.
• Boehmke, Bradley; Greenwell, Brandon (2019). "Bagging". Hands-On Machine Learning with R. Chapman & Hall. pp. 191–202. ISBN 978-1-138-49568-5.