데이터 스트림 클러스터링
Data stream clustering컴퓨터 과학에서 데이터 스트림 클러스터링은 전화 기록, 멀티미디어 데이터, 금융 거래 등 연속적으로 도달하는 데이터의 클러스터링으로 정의된다.데이터 스트림 클러스터링은 보통 스트리밍 알고리즘으로 연구되며, 일련의 포인트들이 주어진 목적은 적은 양의 메모리와 시간을 사용하여 스트림의 좋은 클러스터링을 구성하는 것이다.
역사
데이터 스트림 클러스터링은 최근 대량 스트리밍 데이터를 수반하는 신흥 애플리케이션으로 주목을 받고 있다.클러스터링의 경우 k-means는 널리 사용되는 휴리스틱이지만 k-medoids, CURE, 인기[citation needed] 있는 BICH와 같은 대체 알고리즘도 개발되었다. 데이터 스트림의 경우 첫 결과 중 하나가 1980년에[1] 나타났지만 모델은 1998년에 공식화되었다.[2]
정의
데이터 스트림 클러스터링 문제는 다음과 같이 정의된다.
입력: 미터법 공간의 n개 점 및 정수 k의 시퀀스.
출력:k는 데이터 포인트에서 가장 가까운 클러스터 중심까지의 거리의 합을 최소화하기 위해 n 포인트 집합의 중심에 위치한다.
이것은 k-median 문제의 스트리밍 버전이다.
알고리즘
스트림
스트림(StREAM)은 구하, 미샤, 모트와니, 오칼라한(O'Callahan[3])이 설명한 데이터 스트림을 클러스터링하기 위한 알고리즘으로, k-메디아 문제에 대한 일정한 요소 근사치를 단일 패스 및 작은 공간을 사용하여 달성한다.
정리 — STREAM은 데이터 스트림의 k-Median 문제를 한 번의 통과로 해결할 수 있으며, 여기서 시간 O(n1+e)와 공간 ((nε)은 인자O(1/e) 2까지이며, 여기서 n은 포인트 수와 < 1/ 2
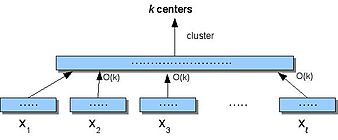
스트림을 이해하려면 첫 번째 단계는 클러스터링이 작은 공간에서 일어날 수 있다는 것을 보여주는 것이다(패스 횟수는 신경 쓰지 않음).스몰 스페이스(Small-Space)는 데이터 를 {\displaystyle 조각으로 나누고 각각(k-means 사용) 클러스터링한 다음 센터가 획득한 클러스터링하는 분할 및 컨커밍 알고리즘이다.
알고리즘 작은 공간(S)
- S를 의 분리 조각 X , 로 나누십시오
- 각 i에 대해 X에서i ( ) 중심을 찾으십시오.X의i 각 점을 가장 가까운 중심에 할당한다.
- X'는 (2)에서 얻은 O ( 중심이며, 여기서 각 중심 c는 할당된 점 수에 따라 가중된다.
- K 센터를 찾으려면 'X군'을(를) 선택하십시오.
Where, if in Step 2 we run a bicriteria -approximation algorithm which outputs at most ak medians with cost at most b times the optimum k-Median solution and in Step 4 we run a c-approximation algorithm then the approximation factor of Small-Space() algorithm is .또한 우리는 Small-Space를 일반화하여 반복적으로 작은 가중 중심 집합에 i를 반복적으로 호출하고 k-median 문제에 대한 일정한 요인 근사치를 달성할 수 있다.
Small-Space의 문제는 우리가 S를 분할하는 하위 집합의 수 이(가) 제한되어 있다는 것이다. 왜냐하면 그것은 X에 중간 중간 중간 중간 중간 중간 중간 중간 중간값들을 메모리에 저장해야 하기 때문이다.기억의 M크기 그래서, 우리는 각 부분 집합 기억,(n/ℓ{\displaystyle n/\ell})에 그 가중ℓ k{\ell k\displaystyle}센터는 또한 메모리에 맞은 맞ℓ{\displaystyle \ell}하위 집합으로 S를 분할하여 필요한ℓ k<>M{\displaystyle \ell k<을 말한다.M}. 하지만 그런 예외 ℓ{\displaystyle \ell.이(가) 항상 존재하는 것은 아닐 수 있다.
STREAM 알고리즘은 중간 중간 중간 중간 중간 중간값 저장 문제를 해결하고 더 나은 실행 시간과 공간 요구사항을 달성한다.알고리즘은 다음과 같이 동작한다.[3]
- 번째 m 점을 입력한다. 이러한[3] 점을 O( ) 예: 2k) 포인트로 줄이기 위해 제시된 임의화된 알고리즘을 사용한다.
- 원본 데이터 지점의 m2/(2k)이 보일 때까지 위의 내용을 반복하십시오.이제 중간 중간 중간 중간계급이 있다.
- 로컬 검색 알고리즘을 사용하여 이러한 m 1단계 중위수를 2k 2차 수준 중위수로 클러스터링하고 계속 진행하십시오.
- 일반적으로 m 레벨-i 중위수를 대부분 유지하고 m을 볼 때 2k 레벨-i+1 중위수를 생성하며, 새 중위수의 가중치는 할당되는 중간 중위수의 가중치의 합으로 한다.
- 원본 데이터 지점을 모두 확인했을 때 원시 이중 알고리즘을 사용하여 모든 중간 중간 중위수를 k 최종 중위수로 군집화한다.[4]
기타 알고리즘
데이터 스트림 클러스터링에 사용되는 기타 잘 알려진 알고리즘은 다음과 같다.
- BUICH:[5] 계층적 데이터 구조를 구축하여 사용 가능한 메모리를 사용하여 수신 지점을 점진적으로 클러스터링하고 필요한 I/O 양을 최소화한다.하나의 패스로 충분한 을 얻을 수 있기 때문에 알고리즘의 복잡성은 ( N) 이다(그러나 여러 패스를 허용하면 결과가 개선된다).
- COBWEB:[6][7] 계층적 클러스터링 모델을 분류 트리 형태로 유지하는 증분식 클러스터링 기법이다.각각의 새로운 지점에 대해 COBWEB는 트리를 내리고, 도중에 노드를 업데이트하고, (범주 효용 함수를 사용하여) 포인트를 배치할 수 있는 가장 좋은 노드를 찾는다.
- C2ICM:[8]클러스터 seeds/initiators고non-seed로 몇몇의 물건들은 가장 범위를 제공한다가 씨앗에 배정된 것을 선택하여 평평한 분할 군집 구조를 구축, 새로운 개체의 덧셈과 점진적인 군집화 새로운 목적과 거짓개의 멤버들 중에는 기존의 낡은 씨앗을 위조하다 새로운 씨앗을 소개할 수 있다.uster는 기존의 새/구식 종자 중 하나에 할당된다.
- CluStream:만약 micro-cluster 새로운 합병 또는 잊현재 micro-clusters data-points과 타임 스탬프 및의, 직선 제곱의 합 분석한 다음 시간에 사람 macro-clust을 창출할 수 있는 지점에 기반을 만들 수 있도록 결정할 수 있[9], BIRCH[5]클러스터 기능 벡터의 시간적 확장 micro-clusters을 사용한다.에 의해 ersK-Means와 같은 오프라인 클러스터링 알고리즘을 사용하여 이러한 마이크로 클러스터링을 클러스터링하여 최종 클러스터링 결과를 생성한다.
참조
- ^ Munro, J.; Paterson, M. (1980). "Selection and Sorting with Limited Storage". Theoretical Computer Science. 12 (3): 315–323. doi:10.1016/0304-3975(80)90061-4.
- ^ Henzinger, M.; Raghavan, P.; Rajagopalan, S. (August 1998). "Computing on Data Streams". Digital Equipment Corporation. TR-1998-011. CiteSeerX 10.1.1.19.9554.
- ^ a b c Guha, S.; Mishra, N.; Motwani, R.; O'Callaghan, L. (2000). "Clustering Data Streams". Proceedings of the Annual Symposium on Foundations of Computer Science: 359–366. CiteSeerX 10.1.1.32.1927. doi:10.1109/SFCS.2000.892124. ISBN 0-7695-0850-2.
- ^ Jain, K.; Vazirani, V. (1999). Primal-dual approximation algorithms for metric facility location and k-median problems. Proc. FOCS. Focs '99. pp. 2–. ISBN 9780769504094.
- ^ a b Zhang, T.; Ramakrishnan, R.; Linvy, M. (1996). "BIRCH: An Efficient Data Clustering Method for Very Large Databases". Proceedings of the ACM SIGMOD Conference on Management of Data. 25 (2): 103–114. doi:10.1145/235968.233324.
- ^ Fisher, D. H. (1987). "Knowledge Acquisition Via Incremental Conceptual Clustering". Machine Learning. 2 (2): 139–172. doi:10.1023/A:1022852608280.
- ^ Fisher, D. H. (1996). "Iterative Optimization and Simplification of Hierarchical Clusterings". Journal of AI Research. 4. arXiv:cs/9604103. Bibcode:1996cs........4103F. CiteSeerX 10.1.1.6.9914.
- ^ Can, F. (1993). "Incremental Clustering for Dynamic Information Processing". ACM Transactions on Information Systems. 11 (2): 143–164. doi:10.1145/130226.134466.
- ^ Aggarwal, Charu C.; Yu, Philip S.; Han, Jiawei; Wang, Jianyong (2003). "A Framework for Clustering Evolving Data Streams" (PDF). Proceedings 2003 VLDB Conference: 81–92. doi:10.1016/B978-012722442-8/50016-1.