활성화 기능

시리즈의 일부
기계 학습 및 데이터 마이닝
문제 분류 클러스터링 회귀 이상 검출 데이터 클리닝 자동 ML 어소시에이션 규칙 강화 학습 구조화된 예측 기능 엔지니어링 기능 학습 온라인 학습 준지도 학습 비지도 학습 순위 매기기 학습 문법 유도
지도 학습 (분류 • 회귀) 의사결정 트리 앙상블 배깅 부스팅 랜덤 포레스트 k-NN 선형 회귀 네이비 베이즈 인공신경망 로지스틱 회귀 분석 퍼셉트론 관련 벡터 머신(RVM) 서포트 벡터 머신(SVM)
클러스터링 버치 치유하다 계층적 k자형 기대 최대화(EM) DBSCAN 광학 평균 이동
치수 축소 인자 분석 CCA ICA LDA NMF PCA PGD t-SNE
구조화된 예측 그래픽 모델 베이즈 네트 조건부 랜덤 필드 히든 마르코프
이상 검출 k-NN 국소 특이치 계수
인공신경망 자동 인코더 인지 컴퓨팅 딥 러닝 딥 드림 다층 퍼셉트론 RNN LSTM GRU ESN 저장고 계산 제한 볼츠만 기계 GAN somerset. 컨볼루션 뉴럴 네트워크 유넷 트랜스포머 비전. 스파이킹 뉴럴 네트워크 메모리 트랜지스터 전기화학 RAM(ECRAM)
강화 학습 Q-러닝 사사 시간차(TD) 멀티 에이전트 셀프 플레이
인간과의 학습 액티브 러닝 크라우드 소싱 휴먼 인 더 루프
모델 진단 학습 곡선
이론. 커널 머신 바이어스-분산 트레이드오프 컴퓨터 학습 이론 경험적 리스크 최소화 오컴 러닝 PAC 학습 통계학 학습 VC 이론
기계학습장 NeurolIPS ICML ML JMLR ArXiv:cs.LG
관련 기사 인공지능 용어집 기계 학습 연구를 위한 데이터 세트 목록 기계학습의 개요
v t

인공신경망에서 노드의 활성화 함수는 입력 또는 입력 세트가 주어진 노드의 출력을 정의한다.표준 집적회로는 입력에 따라 "ON"(1) 또는 "OFF"(0)가 될 수 있는 활성화 기능의 디지털 네트워크로 볼 수 있습니다.이것은 뉴럴 네트워크의 선형 퍼셉트론과 유사합니다.그러나 비선형 활성화 함수만이 이러한 네트워크가 소수의 노드만을 사용하여 중요하지 않은 문제를 계산할 수 있도록 하며, 이러한 활성화 함수를 ^[1]비선형성이라고 한다.

활성화 기능 분류

가장 일반적인 활성화 기능은 리지 기능, 방사형 기능 및 폴드 기능 등 세 가지 범주로 나눌 수 있습니다.

활성화 $함수{\displaystyle }$f {\$displaystyle$$$f$}$는 ${\displaystyle \underset{}{iff}}$ ${\displaystyle \underset{}{lim}}$ v ${\displaystyle \underset{}{\to }}$ ${\displaystyle =\underset{}{}\mathrm{}}$ ${\displaystyle \mathrm{f}}$(${\displaystyle f}$ ${\displaystyle (}$ v ) $=$ 0 { \ $displaystyle$ \$lim$_ {$v \to$ \infty$}$ \$sla$ f$(v)$=$0$ 의 포화 상태에 있습니다.포화 상태가 아니라면 그것은 비포화이다.ReLU와 같은 비포화 활성화 기능은 소멸 ^[2]구배를 겪지 않기 때문에 포화 활성화 기능보다 나을 수 있습니다.

리지 활성화 기능

능선 함수는 입력 변수의 선형 조합에 작용하는 다변량 함수입니다.자주 사용되는 예는 다음과 같습니다.

• $선형{\displaystyle }$ 활성화: ${\displaystyle (}$ (${\displaystyle v\mathbf{}}$ ) $=$ + ${\displaystyle {}^{}b\mathbf{}}$b ${\displaystyle$ \$phi$(\$mathbf$ {$v}$ )=$a+\mathbf {v} '\mathbf {b}$$}$ ,
• ReLU ${\displaystyle 액티베이션}$:${\displaystyle )}$ ( v )${\displaystyle }$=${\displaystyle \max }$( ${\displaystyle {\mathbf{}}^{}}$ , ${\displaystyle a\mathbf{}}$ + v$$ b ) { $displaystyle \phi$( \ $mathbf { v$ } ) $=$ \$max$ ( $0$, $a$+ \ $mathbf${ $v }$ ' \ $mathbf${$b }$) ,
• 중량값 : ( ) a + b> \ $displaystyle \phi$( \ $mathbf${ $v$} ) =$1$_ { $a$+ \ $mathbf${$b }$ ' \ $mathbf${ b } > $0$} ,
• 로지스틱 ${\displaystyle 활성화\mathbf{}}$: : (${\displaystyle }v{\displaystyle }$) ${\displaystyle =}$ ( ${\displaystyle 1}$+ ${\displaystyle \exp }$ ${\displaystyle }$ ( - a${\displaystyle }$- ${\displaystyle v{}^{}b}$b${\displaystyle {}^{}}$) -$$ ( \ $displaystyle \phi$( \ $mathbf { v$ } ) = ( $1$+ \ $expa$ - $\ mathbf${ $v }$ ' \ $mathbf {$b } $)^-1$ )

생물학적으로 영감을 받은 신경망에서 활성화 함수는 보통 ^[3]세포 내에서 활동 전위 발화 속도를 나타내는 추상화이다.가장 간단한 형태로, 이 함수는 2진수이다. 즉, 뉴런이 발화하고 있는지 아닌지이다.$이{\displaystyle }$ 함수는 ${\displaystyle (}$ (${\displaystyle v\mathbf{}}$ ) ${\displaystyle =U}$ (${\displaystyle a}$ + ${\displaystyle {}^{}b}$b$$) { $displaystyle \phi (\mathbf {v}$ ) =$U(a+\mathbf {v} '\mathbf {b$처럼 보입니다. $여기$서$$U {\$displaystyle$ U$}$는 헤비사이드 스텝 함수입니다.

입력 전류가 증가함에 따라 발생하는 점화 속도의 증가를 반영하기 위해 양의 기울기 선을 사용할 수 있습니다.$이러한{\displaystyle }$ 함수는 ${\displaystyle (}$ (${\displaystyle v\mathbf{}}$ ) ${\displaystyle =a}$ + ${\displaystyle {}^{}b\mathbf{}}$b \ $phi$( $\ mathbf$ { v } ) = a + \$mathbf${ v } ' \ $mathbf${ b$$$} 。$

또한 뉴런은 일정 속도보다 빠르게 반응하지 못해 범위가 한정된 S자형 활성화 기능을 자극한다.

방사형 활성화 기능

RBF 네트워크에서는 RBF(Radial Basis Functions)라고 불리는 특별한 종류의 활성화 함수가 사용되며, 이는 범용 함수 근사치로 매우 효율적입니다.이러한 액티베이션 함수는 다양한 형태를 취할 수 있지만 일반적으로 다음 기능 중 하나로 볼 수 있습니다.

• ${\displaystyle 가우스\mathbf{}}$: ${\displaystyle (}$ (${\displaystyle }$v ) ${\displaystyle =}$ ${\displaystyle \exp }$ ${\displaystyle (}$( -${\displaystyle \frac{v\mathbf{}}{}}$v - ${\displaystyle \frac{c\mathbf{}{}^{2\mathrm{}}}{}}$ ${\displaystyle \frac{{}^{}}{\mathrm{}}}$ ${\displaystyle \frac{{2\mathrm{}}^{}}{}}$ 2 ) $=$ \ $exp$ \$phi ($ \ $mathbf${ $v$} - \ $mathbf${ $c$} \ ^ {$2$\ $right }$
• ${\displaystyle 다중}$ 사분율: ${\displaystyle (}$ (${\displaystyle v\mathbf{}}$ ) ${\displaystyle =\sqrt{v\mathbf{}}}$v - ${\displaystyle \sqrt{c\mathbf{}{}^{2\mathrm{}}}}$2 + ${\displaystyle \sqrt{{a\mathrm{}}^{}}}$( \ $displaystyle$ \ , $\ phi$ )$= sq$ rt $\$\ \ $mathbf {$ $v }$ - \ $mathbf${ c } \ $^$ { 2 + $a^$ { $2$$}}}}}}:$
• 역삼원법: ${\displaystyle (}$ (${\displaystyle v\mathbf{}}$ ) ${\displaystyle {}^{}}$ (${\displaystyle {v\mathbf{}}^{}}$v - ${\displaystyle {c\mathbf{}{}^{2\mathrm{}}}^{}}$2 + $a$)${\displaystyle {}^{}}$- 1 ${\displaystyle {\frac{2}{}}^{}}$ ($$\ $displaystyle$ \ , \ $phi$( \ $mathbf${ $v$} )$=$ \ $left$( \ \ $mathbf${ $v }$ - \ $mathbf {$ $c$ } + a^ { $2$ )$}\right)^{-{\frac {1}{2}}}}}$
• 다조화 스플라인

$여기$서 c${\displaystyle \mathbf$ {c$$$}$는 함수 중심을 나타내는 $벡터$이고 {\$displaystyle$ a$}$ 및$$$$${\$ {\$displaystyle \displaystyle}$은 반지름의 확산에 영향을 미치는 파라미터입니다.

폴딩 활성화 기능

접이식 활성화 기능은 컨볼루션 뉴럴 네트워크의 풀링 레이어 및 멀티클래스 분류 네트워크의 출력 레이어에서 광범위하게 사용된다.이러한 활성화는 평균, 최소 또는 최대를 취하는 것과 같은 입력에 대한 집계를 수행합니다.멀티클래스 분류에서는 softmax 액티베이션이 자주 사용됩니다.

활성화 기능 비교

많은 활성화 기능이 있습니다.힌튼 외 연구진의 2012년 자동 음성 인식에 관한 논문은 로지스틱 Sigmoid 활성화 ^[4]기능을 사용한다.2012년의 AlexNet 컴퓨터 비전 아키텍처에서는 ReLU 액티베이션 기능이 사용되며, 2015년의 컴퓨터 비전 아키텍처 ResNet도 마찬가지입니다.2018년식 언어 처리 모델인 BERT는 부드러운 버전의 ReLU인 ^[5]GELU를 사용합니다.

경험적 성과 외에도 활성화 함수는 서로 다른 수학적 특성을 가지고 있다.

비선형

활성화 함수가 비선형일 경우, 2층 뉴럴 네트워크가 범용 함수 ^[6]근사치임을 증명할 수 있습니다.이것은 보편적 근사 정리라고 알려져 있다.ID 활성화 함수가 이 속성을 충족하지 않습니다.여러 레이어가 아이덴티티 액티베이션 기능을 사용하는 경우 네트워크 전체는 단일 레이어 모델과 동일합니다.

범위

활성화 함수의 범위가 유한할 경우 패턴 표시가 제한된 체중에만 유의하게 영향을 미치기 때문에 구배 기반 훈련 방법이 더 안정적인 경향이 있다.범위가 무한할 경우 패턴 표시가 대부분의 체중에 큰 영향을 미치기 때문에 일반적으로 훈련이 더 효율적입니다.후자의 경우 일반적으로 더 적은 학습률이 필요합니다.^{[citation needed]}

지속적 차별화 가능

이 속성은 구배 기반 최적화 방식을 활성화하기 위해 바람직합니다(ReLU는 지속적으로 차별화되지 않으며 구배 기반 최적화에 문제가 있지만 여전히 가능합니다).바이너리 스텝액티베이션 함수는 0에서는 미분할 수 없고 다른 모든 값에 대해0으로 미분되므로 그라데이션 기반 메서드는 이 ^[7]함수로 진행할 수 없습니다.

이러한 특성은 성능에 결정적으로 영향을 주지 않으며, 유용할 수 있는 유일한 수학적 특성도 아닙니다.예를 들어 softplus의 엄격한 양의 범위는 가변 자동 인코더의 변동을 예측하는 데 적합합니다.

활성화 함수 표

다음 표에서는 이전 레이어에서 한 겹 x의 함수인 여러 활성화 함수의 속성을 비교합니다.

이름.	줄거리.	함수${\displaystyle ,}$ ${\displaystyle g}$ (${\displaystyle }$x$$) {$displaystyle$ g$(x)}$	g$${\$displaystyle$ g$\}$ , $g{\displaystyle {}^{}(}$ (${\displaystyle x}$) {$displaystyle$ g$'(x)}$의 도함수	범위	연속 순서
신원		${\displaystyle x}$	${\displaystyle 1}$	${\displaystyle(-\infty,\infty)}$	${\displaystyle C^{\infty}}$
바이너리 스텝		${\displaystyle {case} 0&{\text{if}}x <0\\1&{\text{if}}x\geq 0\end{case}}$	${\displaystyle {cases} 0&{\text{cases}}x\{\text{cases}}x=0\end{cases}}$	${\displaystyle\{0,1\}}$	${\displaystyle C^{-1}}$
로지스틱, Sigmoid 또는 소프트 스텝		${\displaystyle(x)\doteq{1+e^{-x}}}$	$\displaystyle g(x)(1-g(x))}$	${\displaystyle(0,1)}$	${\displaystyle C^{\infty}}$
쌍곡선 탄젠트(tanh)		$\displaystyle \tanh(x)\doteq {frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}$	${{displaystyle 1-g(x)^{2}}$	${\displaystyle(-1,1)}$	${\displaystyle C^{\infty}}$
정류 선형 장치(ReLU)[8]		${{displaystyle {displaystyle}{+}\doteq {case}}x\leq 0\x&{\text{if}}x>0\end {cases}\={}&\max(0,x)=xtextb {1}{x>0}\end}}} 정렬$	${\displaystyle {case} 0&{\text{if}}x<0\\1&{\text{if}}x>0\{\text{case}}x=0\end{case}}}$	$(\displaystyle [0,\infty])$	${\displaystyle C^{0}}$
가우스 오차 선형 단위(GELU)[5]		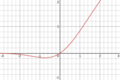${\displaystyle {\frac {1}{2}}x\left(1+{\text{erf}}\left\frac {x}{\displayrt {2}}\right}\right)\\{}={}&x\Phi(x)\end{aligned}}$	$\Displaystyle \Phi(x)+x\phi(x)}$	$(\displaystyle(-0.17\ldots,\infty))$	${\displaystyle C^{\infty}}$
소프트플러스[9]		$\displaystyle \ln \left(1+e^{x}\오른쪽)}$	$(\displaystyle\frac{1}{1+e^{-x}}})$	${\displaystyle (0,\infty)}$	${\displaystyle C^{\infty}}$
지수 선형 단위(ELU)[10]		$\displaystyle \alpha \left(e^{x}-1\right)&{\text{if}x\leq 0\x&{\text{if}x>0\end{cases}}}$ $(\displaystyle$\alpha$)$를 지정합니다.	${\displaystyle {case}\alpha e^{x}&{\text{if}}x>0\1&{\text{if}}x=0\text{및}}}\alpha=1\end{case}}}}x$	${\displaystyle(-\alpha,\infty)}$	${\displaystyle\case\case}C^{1}&{\text{if}}\alpha=1\C^{0}&{\text{othery}}\end{case}}$
스케일링 지수 선형 단위(SELU)[11]		${\displaystyle \displayda {case}\alpha(e^{x}-1)&{\text{x}x&{\text{if}}x\geq 0\end{case}}$ $파라미터{\displaystyle }$ $({displaystyle \displayda = 1.0507})$ $및$ α ${\displaystyle =\mathrm{}}$1.$({displaystyle \alpha = 1.67326)$의 경우	${\displaystyle\displayda\alpha e^{x}&{\text{if}}x <0\\1&{\text{if}}x\geq 0\end{cases}}}$	$(\displaystyle(-\displayda \alpha,\infty))$	${\displaystyle C^{0}}$
누출 수리 선형 장치(누출 ReLU)[12]		${\displaystyle {case} 0.01x&{\text{if}}x&{\text{if}}x\geq 0\end{case}}$	${\displaystyle {case} 0.01&{\text{if}}x<0\\1&{\text{if}}x\{\text{case}}x=0\end{case}}}$	${\displaystyle(-\infty,\infty)}$	${\displaystyle C^{0}}$
파라메트릭 정류 선형 장치(PRe)LU)[13]		${\displaystyle {case}\alpha x&{\text{if}}x&{\text{if}}x\geq 0\end{case}}$ $(\displaystyle$\alpha$)$를 지정합니다.	${\displaystyle {case}\alpha &{\text{if}}x <0\\1&{\text{if}}x\geq 0\end{case}}$	${\displaystyle(-\infty,\infty)}$	${\displaystyle C^{0}}$
Sigmoid 선형 단위(SiLU,[5] Sigmoid 수축,[14] SiL [15]또는 Swish-1[16])		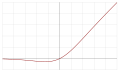$(\displaystyle\frac{x}{1+e^{-x}}})$	${{displaystyle {1+e^{-x}+xe^{-x}}{\left(1+e^{-x}\right)^{2}}}}$	$(\displaystyle [-0.278\ldots,\infty])$	${\displaystyle C^{\infty}}$
가우스		${\displaystyle e^{-x^{2}}}$	$(\displaystyle - 2xe^{-x^{2}})$	${\displaystyle(0,1)}$	${\displaystyle C^{\infty}}$

다음 표에는 이전 레이어에서 가져온 단일 폴드 x의 기능이 아닌 활성화 기능이 나열되어 있습니다.

이름.	식, ${\displaystyle g_{}}$i ( ${\displaystyle x\stackrel{}{}}$ ${\displaystyle \to }$) { $displaystyle$ g $_${ i$$} \ $left$vac \ $vec${ $x$} \ right$$}	파생상품,${\displaystyle \frac{\mathrm{}{\delta gi}_{}}{}}$( ${\displaystyle \frac{x\stackrel{}{}}{}}$ ${\displaystyle \frac{\to }{}}$ )${\displaystyle \frac{}{\mathrm{}{\delta x}_{}}}$ j$$(\$displaystyle {frac g_{i}\leftvec {x}}{\right}}$ {\$display$ x_${j}}}$	범위	연속 순서
소프트맥스	${\displaystyle \frac{{e{}_{}}^{}}{}}$ ${\displaystyle \frac{{x_{}}^{}}{}}$ i${\displaystyle \frac{{{}_{}}^{}}{\underset{j}{\overset{}{}}}}$ j ${\displaystyle \frac{\underset{}{\overset{}{=}}}{}}$ ${\displaystyle \frac{\underset{}{\overset{}{1}}}{}}$ ${\displaystyle \frac{\underset{}{\overset{}{}}{}^{}}{}}$ ${\displaystyle \frac{{e{}_{}}^{}}{}}$ x$$ (\$displaystyle {e^{x_{i}})$ {\$sum$_ {$j=1}^{J} e^{x_{j}}}($i = 1, …, J)	$(\displaystyle g_{i}\leftvec {x}\right)\left(\displaystyle _ {ij}-g_{j}\leftvec {x}\right)})$[1][2]	${\displaystyle(0,1)}$	${\displaystyle C^{\infty}}$
최대[17] 출력	$\displaystyle \max _{i}x_{i}$	${\displaystyle {cases}1&{\text{if}}j={\operatorname {i}},x_{i}\\0&{\text{cases}}j\neq {\underset {i}}{\operatorname {cases}}}},x_i}\end{cases}$	${\displaystyle(-\infty,\infty)}$	${\displaystyle C^{0}}$

^ 여기서 ${\displaystyle {\delta }_{}}$ ${\displaystyle i_{}}$j \ $display style$ _ { $ij$}는$$ Kronecker 델타입니다.

^ 예를 들어 j$\displaystyle$는 이전$$ 뉴럴 네트워크 계층의 커널 수를 통해 반복되는 반면 $\displaystyle$i는 현재 계층의 커널 수를 통해 반복될$$ 수 있습니다.

「 」를 참조해 주세요.

• 로지스틱 함수
• 정류기(신경 네트워크)
• 안정성(학습 이론)
• Softmax 함수

레퍼런스