가변 오토인코더

시리즈의 일부(on)
머신 러닝 데이터 마이닝(data mining)
패러다임 지도학습 비지도 학습 온라인 학습 일괄 학습 메타학습 준지도 학습 자기주도학습 강화학습 규칙 기반 학습 양자기계학습
문제 분류 생성모델 회귀 클러스터링 치수 축소 밀도추정 이상 탐지 데이터 정리 오토ML 연관규칙 의미분석 구조예측 피쳐 엔지니어링 특징 학습 랭킹을 익히는 법 문법유도 온톨로지 학습 멀티모달 학습
지도학습 (분류 • 회귀분석) 도제학습 의사결정나무 앙상블 배깅 부스팅 랜덤 포레스트 k-NN 선형회귀분석 나이브 베이즈 인공신경망 로지스틱 회귀 분석 퍼셉트론 연관성 벡터 머신(RVM) 서포트 벡터 머신(SVM)
클러스터링 버치 치유하다 계층적 k- 퍼지 기대-최대화(EM) DBSAN 옵틱스 평균이동
차원 축소 요인분석 CCA ICA LDA NMF PCA PGD t-SNE SDL
구조예측 그래픽 모델 베이즈넷 조건부 랜덤 필드 히든 마코프
이상 탐지 RANSAC k-NN 국소이상치인자 고립림
인공신경망 오토인코더 인지 컴퓨팅 딥러닝 딥 드림 피드포워드 신경망 순환신경망 LSTM GRU ESN 저장고 계산 제한된 볼츠만 기계 GAN 확산모델 SOM 컨볼루션 신경망 유넷 트랜스포머 비전. 스파이킹 신경망 멤트랜지스터 전기화학 램(ECRAM)
강화학습 Q-러닝 사르사 시간차(TD) 멀티 에이전트 셀프 플레이
인간과의 학습 능동적 학습 크라우드소싱 휴먼 인 더 루프
모델진단 학습곡선
수학적 기초 커널 머신 치우침-분산 트레이드오프 컴퓨터 학습 이론 경험적 리스크 최소화 오캄 학습 PAC 학습 통계학습 VC이론
기계학습 장소 ECML PKDD 뉴립스 ICML ICLR IJCAI ML JMLR
관련기사 인공지능 용어집 머신러닝 연구용 데이터셋 목록 컴퓨터 비전 및 이미지 처리 분야의 데이터셋 목록 기계학습 개요
v t

기계 학습에서 변형 오토인코더(VAE)는 Dieerik P. Kingma와 Max Welling에 의해 도입된 인공 신경망 아키텍처입니다.그것은 확률론적 그래픽 모델과 가변 베이지안 방법군의 일부입니다.^[1]

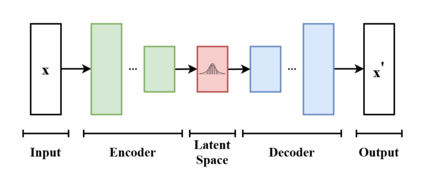
변형 오토인코더는 아키텍처 친화성 때문에 오토인코더 모델과 종종 연관되지만 목표 및 수학적 공식에서 상당한 차이가 있습니다.가변 오토 인코더는 신경망을 전체 구조의 일부로만 요구하는 확률론적 생성 모델입니다.뉴럴 네트워크 컴포넌트들은 일반적으로 제1 컴포넌트 및 제2 컴포넌트에 대해 각각 인코더 및 디코더로 지칭됩니다.첫 번째 신경망은 입력 변수를 변동 분포의 매개 변수에 대응하는 잠재 공간에 매핑합니다.이러한 방식으로 인코더는 동일한 분포에서 오는 여러 개의 다른 샘플을 생성할 수 있습니다.디코더는 데이터 포인트를 생성하거나 생성하기 위해 잠재 공간에서 입력 공간으로 매핑하는 반대 기능을 가지고 있습니다.일반적으로 두 네트워크는 재파라미터화 트릭의 사용과 함께 훈련되지만 노이즈 모델의 분산은 별도로 학습할 수 있습니다.

이러한 유형의 모델은 처음에는 비지도 학습을 위해 설계되었지만,^[2][3] 준지도 학습^[4][5] 및 지도 학습에 대한 효과가 입증되었습니다.^[6]

아키텍처 및 운영 개요

가변 오토인코더는 사전 분포와 노이즈 분포가 각각 있는 생성 모델입니다.일반적으로 이러한 모델은 기대-최대화 메타 알고리즘(예: 확률론적 PCA, (스파이크 & 슬라브) 희소 코딩)을 사용하여 훈련됩니다.이러한 방식은 일반적으로 다루기 힘든 데이터 가능성의 하한을 최적화하며, 이를 위해서는 q-분포 또는 변형 포스터를 발견해야 합니다.이러한 q-분포는 일반적으로 별도의 최적화 프로세스에서 각 개별 데이터 점에 대해 모수화됩니다.그러나 가변형 오토 인코더는 신경망을 상각형 접근법으로 사용하여 데이터 포인트 간에 공동으로 최적화합니다.이 신경망은 데이터 포인트 자체를 입력으로 받아 변동 분포를 위한 파라미터를 출력합니다.알려진 입력 공간에서 저차원 잠재 공간으로 매핑하기 때문에 인코더(encoder)라고 합니다.

디코더는 이 모델의 두 번째 신경망입니다.이 기능은 잠재 공간에서 입력 공간으로 매핑하는 기능입니다. 예를 들어 소음 분포의 수단으로 사용됩니다.분산에 매핑되는 다른 신경망을 사용할 수 있지만 단순화를 위해 이는 생략할 수 있습니다.이러한 경우에는 기울기 강하를 사용하여 분산을 최적화할 수 있습니다.

이 모형을 최적화하려면 "재구성 오류"와 쿨백-라이블러 발산이라는 두 용어를 알아야 합니다.두 항은 모두 확률론적 모델의 자유 에너지 표현식에서 파생된 것이므로, 소음 분포와 가정된 데이터 이전에 따라 다릅니다.예를 들어, IMAGENET과 같은 표준 VAE 작업은 일반적으로 가우스 분포 노이즈를 갖는 것으로 가정되지만, 이진화된 MNIST와 같은 작업은 Bernouli 노이즈를 필요로 합니다.자유 에너지 표현식의 KL-D는 p-분포와 중복되는 q-분포의 확률 질량을 최대화하며, 불행하게도 모드 탐색 행동을 초래할 수 있습니다."재구성" 항은 자유 에너지 표현식의 나머지 부분이며, 기대 값을 계산하려면 샘플링 근사치가 필요합니다.^[7]

공식화

확률적 모델링의 관점에서, 데이터 $x$ ${\displaystyle x}$의 가능성을 그들이 선택한 매개 변수화된 확률 분포 $p$ θ${\displaystyle {}_{}}$(${\displaystyle x)}$ = ${\displaystyle p}$(${\displaystyle x}$ θ${\displaystyle )}$ ${\displaystyle p_{\theta}(x$) = $p(x \theta )}$로 극대화하고자 합니다$.$이 분포는 보통 $\mu$ ${\displaystyle$\mu}와$$σ ${\displaystyle \sigma}$로 매개 변수화되는 가우스 $(x$,${\displaystyle }$σ${\displaystyle )}$ ${\displaystyle$ \$mu,\sigma}$로 선택되며, 지수 패밀리의 구성원으로서 노이즈 분포로 작업하기 쉽습니다.단순 분포는 최대화하기에 충분히 쉽지만, 잠재 상태 $z{\displaystyle }$ ${\displaystyle z}$보다 우선순위가 가정된 분포는 다루기 힘든 적분으로 이어집니다$$.$z$ ${\displaystyle z}$에 대한 주변화를 통해 $p$ θ${\displaystyle {}_{}}$(${\displaystyle x)}$ ${\displaystyle p_{\theta}(x)$를 찾도록 합시다$.$

${\displaystyle p_{\theta}(x)=\int_{z}p_{\theta}({x,z})\, dz,}$

여기서 $p$ θ${\displaystyle {}_{}}$(${\displaystyle x,}$ z${\displaystyle )}$ ${\displaystyle p_{\theta}({x,z})}$는 관측 가능한 $데이터$ x ${\displaystyle x}$의 $p$ θ ${\displaystyle p_{\theta}}$와 그 잠재적 표현 또는 $인코딩$ z$${\$displaystyle z}$에 따른 공동 분포를 나타냅니다$.$ 체인 규칙에 따라 방정식은 다음과 같이 다시 쓸 수 있습니다.

${\displaystyle p_{\theta}(x)=\int_{z}p_{\theta}({x z})p_{\theta}(z)\,dz}$

바닐라 가변 오토인코더에서 $z$ ${\displaystyle z}$는 일반적으로 실수의 유한 차원 벡터로 $간주$되고 ${\displaystyle p_{}}$ θ${\displaystyle }$(${\displaystyle x}$z) {\$displaystyle$p_{\$theta$}({x z$})$는 가우스 분포로 간주됩니다.그렇다면 $p$ θ (${\displaystyle {}_{}}$x${\displaystyle }$) ${\displaystyle p_{\theta}(x)}$는 가우스 분포의 혼합입니다.

이제 입력 데이터와 잠재적 표현 사이의 관계 집합을 다음과 같이 정의할 수 있습니다.

• 이전 $p$ θ (${\displaystyle {}_{}z)}$ ${\displaystyle p_{\theta}(z)}$
• 우도 $p$ θ${\displaystyle {}_{}x}$ ${\displaystyle z)}$ ${\displaystyle p_{\theta}(x z)}$
• $사후$ p θ${\displaystyle {}_{}z}$ ${\displaystyle x}$) ${\displaystyle p_{\theta}(z x)}$

안타깝게도 $p$ θ${\displaystyle {}_{}}$(${\displaystyle z}$ ${\displaystyle x}$) ${\displaystyle p_{\theta}(z x)}$의 계산은 비싸고 대부분의 경우 다루기 어렵습니다.미적분학의 속도를 높이기 위해, 다음과 같이 후분포를 근사화하는 추가 함수를 도입할 필요가 있습니다.

${\displaystyle q_{\phi}({z x})\approx p_{\theta}({z x})}$

$q$ ${\displaystyle$ \$phi$}을$($를) 매개 변수화하는 실수 값의 집합으로 정의된 ϕ ${\$displaystyle q}. 좋은$$$q$ ϕ ${\displaystyle q_{\phi$}}을$($를) 찾는 데 "투자$"$함으로써 나중에 적분을 $하지$ 않고 x ${\displaystyle$ x}에서$$z ${\displaystyle$ z}을$($를) 빠르게 추론할 수 있기 때문에 이를 상각 추론이라고도 합니다.

이러한 방식으로 문제는 좋은 확률적 자동 인코더를 찾는 것인데, 조건부 우도 분포 $p$ θ ${\displaystyle {}_{}x}$ z${\displaystyle )}$ ${\displaystyle p_{\theta}(x$ z$)}$는 확률적 디코더에서 계산되고 근사 후방 분포 $q$ ϕ ${\displaystyle {}_{}z}$ ${\displaystyle x)}$ ${\displaystyle q_{\phi}(z$ x$)}$는 확률적 인코더에서 계산됩니다.

인코더를 $E$ ϕ ${\displaystyle E_{\phi}}$로, 디코더를 D$$θ {\displaystyle $D_${\$theta}}$로 매개$$변수화합니다$.$

증거 하한(ELBO)

모든 딥 러닝 문제에서와 마찬가지로, 역전파를 통해 네트워크 가중치를 업데이트하기 위해 차별화 가능한 손실 함수를 정의할 필요가 있습니다.

가변 오토 인코더의 경우, 생성 모델 매개 변수 θ ${\displaystyle \theta}$를 공동으로 최적화하여 입력과 출력 간의 재구성 오류를 줄이고, ϕ ${\displaystyle$\phi$}$를 ϕ하여 $q$ θ${\displaystyle {}_{}z}$ ${\displaystyle x}$${\displaystyle )}$ ${\displaystyle q_{\phi}({z x})$를 $p$ θ${\displaystyle {}_{}z}$ ${\displaystyle x}$) ${\displaystyle p_{\theta}(z x)}$에 최대한 가깝게 만드는 것이 아이디어입니다$.$ 다시 생각해보십시오.평균 제곱 오차 및 교차 엔트로피는 종종 사용됩니다.

두 분포 사이의 거리 손실로 Kullback-Leibler 발산 ${\displaystyle {\mathrm{DKL}}_{}}$ ${\displaystyle {}_{}{}_{}}$ ϕ${\displaystyle {}_{}}$( z ${\displaystyle x}$ )${\displaystyle }$∥ ${\displaystyle {}_{}}$ θ (${\displaystyle {}_{}}$z ${\displaystyle x}$)${\displaystyle D_{KL}(q_{\phi }({z x})\paralle p_{\theta}({z$ x$})$는 p θ${\displaystyle {}_{}}$($z$ x${\displaystyle )}$${\$$displaystyle p_{\phi }({$$z x$$})$ 아래에 $q$ ϕ ${\displaystyle {}_{}z}$ x})를 압축하는 것이 좋습니다$.$

방금 정의된 거리 손실은 다음과 같이 확장됩니다.

${\displaystyle {\begin{aligned}D_{KL}(q_{\phi}({z x})\parallel p_{\theta}({z x})&=\mathbb {E} _{z\sim q_{\phi}(\cdot x)}\left[\ln {\frac {q_{\phi}(z x)}{p_{\theta}(z x)}\right]\\&=\mathbb {E} _{z\sim q_{\phi}(\cdot x)}\left[\ln {\frac {q_{\phi}({z x})p_{\theta}(x)}{p_{\theta}(x,z)}\right]\\&=\ln p_{\theta}(x)+\mathbb {E} _{z\sim q_{\phi}(\cdot x)}\left[\ln{\frac {q_{\phi}({z x})}{p_{\theta}(x,z)}\right]\end{aligned}}$

이제 증거 하한(ELBO)을 정의합니다.

ELBO 극대화는 ${\displaystyle \ln }$ ⁡ ${\displaystyle {}_{}}$ θ (${\displaystyle {}_{}}$x${\displaystyle }$) ${\displaystyle \ln p_{\theta}(x))$를 동시에 최대화하고 ${\displaystyle {\mathrm{DKL}}_{}}$(${\displaystyle {}_{}}$ ϕ${\displaystyle {}_{}}$( ${\displaystyle z}$ ${\displaystyle x}$)${\displaystyle }$∥ ${\displaystyle {}_{}}$ θ (${\displaystyle {}_{}z}$ ${\displaystyle x}$) ${\displaystyle D_{KL}(q_{\phi}({z$ x$})\parallel p_{\theta}({z$ x$})$를 최소화하는 것과 같습니다$.$즉, 관측된 데이터의 로그 가능성을 최대화하고, 정확한 $후방$ p θ${\displaystyle (}$⋅ ${\displaystyle x)}$ ${\displaystyle p_{\theta}(\cdot x)}$에서 근사 후방 $q$ ϕ${\displaystyle {}_{}}$⋅ ${\displaystyle x}$) ${\displaystyle q_{\phi}(\cdot$ x$)}$의 발산을 최소화합니다$.$

주어진 형태는 최대화에 그다지 편리하지는 않지만, 다음과 같은 동등한 형태가 있습니다.

여기서 ${\displaystyle \ln }$ ⁡ ${\displaystyle {}_{}}$ θ${\displaystyle {}_{}x}$ z${\displaystyle )}$ ${\displaystyle \ln p_{\theta}(x$ z$)}$는$$- ${\displaystyle \frac{12}{}}$ ‖ ${\displaystyle x}$- ${\displaystyle {}_{}}$ θ${\displaystyle {}_{}z)}$ ‖ ${\displaystyle {}_{}^{}}${\$displaystyle -{\frac {1}{2}}\ x-D_{\theta }(z)\ _{2}^{2$ 즉, 가산 상수까지 $x$ ~${\displaystyle }$N (${\displaystyle {}_{}}$ θ${\displaystyle {}_{}z),}$ ${\displaystyle I}$) ${\displaystyle x\sim {\mathcal {N}}(D_{\theta }(z),$$I)}$이(가) 산출됩니다.즉, $z$ ${\displaystyle z}$ 조건부 $x$ ${\displaystyle x}$ 분포를 $D$ θ(${\displaystyle z)}$ ${\displaystyle d_{\theta}(z)}$ 중심의 가우스 분포로 모델링합니다$.$q ϕ (${\displaystyle {}_{}}$z ${\displaystyle x}$ ) ${\displaystyle q_{\phi }($z $x)}$와 p θ (${\displaystyle z{}_{}}$ ${\displaystyle p_{\theta}(z)}$의 분포도 종종 가우스파로 선택됩니다. $z$ x ~${\displaystyle N}$ ( ${\displaystyle E}$ϕ (${\displaystyle {}_{}x}$ ${\displaystyle ),}$σ ϕ ( x${\displaystyle {}_{}}$)$2$ ${\displaystyle I^{}}$ ) ${\displaystyle$ z x$\sim {\mathcal$ {$N}(x),\sigma$ _${\phi }(x)^{2}I ),$ z $~{\displaystyle }N$ (${\displaystyle 0,I}$ ) ${\displaystyle$ z$\sim {\mathcal$ {$N}($0,$I),$가우스인의 KL 발산에 대한 공식을 통해 얻을 수 있습니다.여기서 $N{\displaystyle }$ ${\displaystyle N}$은(는$)$ z {\$displaystyle z}$의 차원입니다$.$ ELBO와 ELBO의 극대화에 대한 더 자세한 파생 및 해석은 해당 메인 페이지를 참조하십시오.

매개변수 재설정

효율적으로 검색하려면 다음과 같이 하십시오.

대표적인 방법은 경사 하강입니다.

찾는 것은 간단합니다.

하지만,$확률$ 분포 자체에 {\$displaystyle$ \$phi }$ϕ이(가) 나타나기 때문에$$${\$$displaystyle \nabla _{\phi$}}을(를) 예상 내부에 넣을 수 없습니다.재파라미터화 트릭(확률적 역전파라고도^[9] 함)은 이 어려움을 우회합니다.^[7][10][11]

가장 중요한 예는 $z$ ~${\displaystyle {}_{}}$ ϕ (${\displaystyle {}_{}}$⋅${\displaystyle x}$ )$${\$displaystyle$ z$\sim q_{\phi }(\cdot$ x${\displaystyle ))}$ {\$displaystyle {\mathcal {N}}(\mu _{\phi }(x)),\Sigma$ _${\phi }(x))}(x$))가 정규 분포일 때입니다$.$

ε ~${\displaystyle N}$ ( 0${\displaystyle ,}$ ${\displaystyle I)}$ ${\displaystyle {\boldsymbol {\varepsilon}}\sim {\mathcal$ {$N}}($0, ${\boldsymbol$ {$I})}을($를) "$표준$ 난수 생성기"로 지정하고 $z$ ${\displaystyle z}$를 $z$ =$$ ϕ (${\displaystyle {}_{}}$x${\displaystyle }$)${\displaystyle }$+ ${\displaystyle {}_{}}$ ϕ ( ${\displaystyle x{}_{}}$)${\displaystyle }$ϵ ${\displaystyle$ z=\$mu$ _${\phi }(x)+$로 구성합니다.$L_{\phi }(x)\epsilon$ 여기서 $L$ $ϕ$ ${\displaystyle {}_{}x)}$ ${\displaystyle L_{\phi }(x)}$는 촐레스키 분해에 의해 얻어집니다.

그러면 저희가.그래서 확률적 기울기 하강을 허용하는 편향되지 않은 기울기 추정치를 구했습니다.

$z$ ${\displaystyle z}$을(를) 매개 변수화하였으므로$$$q$ ϕ (${\displaystyle z}$ ${\displaystyle q_{\phi}(z x)}$을(를) 찾아야 합니다$.$ ϵ ${\displaystyle \epsilon}$에 대한 확률 밀도 함수로 $q$ ${\displaystyle 0_{}}$ ${\displaystyle q_{0}$이라고 하면 됩니다$.$

여기서 ∂ ϵ ${\displaystyle {}_{}}$ ${\displaystyle \$partial $_{\epsilon}z}$는 z ${\displaystyle z}$에 대한 ϵ ${\displaystyle \epsilon}}$의 야코비안 행렬입니다$.$ $z$ = ${\displaystyle {}_{}}$ ϕ${\displaystyle {}_{}}$(${\displaystyle x)}$+ ${\displaystyle {}_{}}$ ϕ ${\displaystyle {}_{}x)}$ ϵ ${\displaystyle$z =\$mu _{\phi}(x)+$$L_{\phi }(x)\epsilon$ 이것은

변주곡

아키텍처를 다른 도메인에 적응시키고 성능을 향상시키기 위해 다양한 자동 인코더 응용 프로그램과 확장 프로그램이 사용되었습니다.

${\displaystyle \beta }$ ${\displaystyle \beta$} -$$VAE는$$ 인수화된 잠재 표현을 자동으로 발견하고 해석하기 위해 가중 Kullback-Leibler 발산항을 가진 구현입니다.이 구현을 사용하면 1보다 큰 $\beta {\displaystyle }$ ${\displaystyle \beta}$ 값에$$ 대해 매니폴드 분리를 강제할 수 있습니다.이 아키텍처는 감독 없이도 해체된 잠재 요인을 발견할 수 있습니다.^[12][13]

조건부 VAE(CVAE)는 잠재 공간에 레이블 정보를 삽입하여 학습된 데이터의 결정론적 제한 표현을 강제합니다.^[14]

일부 구조는 생성된 샘플의^[15][16] 품질을 직접 다루거나 둘 이상의 잠재 공간을 구현하여 표현 학습을 더욱 향상시킵니다.^[17][18]

일부 아키텍처는 하이브리드 모델을 얻기 위해 VAE와 생성적 적대 네트워크를 혼합합니다.^[19][20][21]

참고 항목

참고문헌