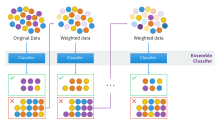
활성화(기계학습)

시리즈의 일부
기계 학습 및 데이터 마이닝
문제 분류 클러스터링 회귀 이상 검출 데이터 클리닝 자동 ML 어소시에이션 규칙 강화 학습 구조화된 예측 기능 엔지니어링 기능 학습 온라인 학습 준지도 학습 비지도 학습 순위 매기기 학습 문법 유도
지도 학습 (분류 • 회귀) 의사결정 트리 앙상블 배깅 부스팅 랜덤 포레스트 k-NN 선형 회귀 네이비 베이즈 인공신경망 로지스틱 회귀 분석 퍼셉트론 관련 벡터 머신(RVM) 서포트 벡터 머신(SVM)
클러스터링 버치 치유하다 계층적 k자형 기대 최대화(EM) DBSCAN 광학 평균 이동
치수 축소 인자 분석 CCA ICA LDA NMF PCA PGD t-SNE
구조화된 예측 그래픽 모델 베이즈 네트 조건부 랜덤 필드 히든 마르코프
이상 검출 k-NN 국소 특이치 계수
인공신경망 자동 인코더 인지 컴퓨팅 딥 러닝 딥 드림 다층 퍼셉트론 RNN LSTM GRU ESN 저장고 계산 제한 볼츠만 기계 GAN somerset. 컨볼루션 뉴럴 네트워크 유넷 트랜스포머 비전. 스파이킹 뉴럴 네트워크 메모리 트랜지스터 전기화학 RAM(ECRAM)
강화 학습 Q-러닝 사사 시간차(TD) 멀티 에이전트 셀프 플레이
인간과의 학습 액티브 러닝 크라우드 소싱 휴먼 인 더 루프
모델 진단 학습 곡선
이론. 커널 머신 바이어스-분산 트레이드오프 컴퓨터 학습 이론 경험적 리스크 최소화 오컴 러닝 PAC 학습 통계학 학습 VC 이론
기계학습장 NeurolIPS ICML ML JMLR ArXiv:cs.LG
관련 기사 인공지능 용어집 기계 학습 연구를 위한 데이터 세트 목록 기계학습의 개요
v t

기계 학습에서 부스팅은 주로 편견을 줄이고 또한 감독[1] 학습의 차이를 줄이기 위한 앙상블 메타 알고리즘이며, 약한 학습자를 강한 ^[2]학습자로 변환하는 기계 학습 알고리즘의 집합이다.상승은 Kearns와 Valiant(1988, 1989)^[3][4]에 의해 제기된 질문에 기초한다: "약한 학습자 집합이 하나의 강한 학습자를 만들 수 있는가?"약한 학습자는 진정한 분류와 약간만 상관되는 분류자로 정의된다(임의의 추측보다 예에 더 나은 레이블을 붙일 수 있다).반대로, 강한 학습자는 진정한 분류와 임의로 잘 연관된 분류자입니다.

로버트 샤파이어는 1990년^[5] '켄스와 발리언트'에 대한 질문에 대한 긍정적인 답변으로 기계 학습과 통계학에 상당한 영향을 미쳤으며,^[6] 가장 주목할 만한 것은 부스팅의 발전으로 이어졌다.

처음 도입되었을 때, 가설 부양의 문제는 단순히 약한 학습자를 강한 학습자로 바꾸는 과정이었다."비공식적으로, [가설 부스트] 문제는 [약한 학습자]^[3]의 성과가 무작위 추측보다 약간 더 나은 가설을 출력하는 효율적인 학습 알고리즘[…]이 임의의 정확도[즉 강한 학습자]의 가설을 출력하는 효율적인 알고리즘의 존재를 의미하는지 여부를 묻는다."가설 증강을 빠르게 달성하는 알고리즘은 단순히 "증강"으로 알려지게 되었다.프라운드와 샤파이어의 아크(Adapt[at]iv Resampling and Combining)^[7]는 일반적인 기술로서 ^[8]부스팅과 거의 동의어이다.

부스트 알고리즘

부스팅은 알고리즘적으로 제한되지 않지만, 대부분의 부스팅 알고리즘은 분포에 관한 약한 분류기를 반복적으로 학습하고 그것들을 최종적인 강한 분류기에 추가하는 것으로 구성된다.그것들을 더하면, 약한 학습자의 정확도와 관련된 방식으로 가중치가 부여됩니다.약한 학습자가 추가되면 데이터 가중치가 재조정됩니다. 이를 "재 가중치"라고 합니다.잘못 분류된 입력 데이터는 가중치가 높아지고 올바르게 분류된 예는 ^{[note 1]}가중치가 감소합니다.따라서 미래의 약한 학습자는 이전의 약한 학습자가 잘못 분류한 예에 더 집중한다.

부스팅 알고리즘이 많이 있습니다.Robert Schapire(재귀적 다수결 공식)^[5]와 Yoav Freund(다수에 ^[9]의한 증가)에 의해 제안된 원래의 것들은 적응력이 없었고 약한 학습자들을 충분히 이용할 수 없었다.Schapire와 Freund는 그 후 AdaBoost, 적응형 부스팅 알고리즘을 개발하여 권위 있는 Gödel Prize를 수상했습니다.

아마도 거의 정확한 학습 공식에서 입증 가능한 부스트 알고리즘만 정확하게 부스트 알고리즘이라고 할 수 있다.부스트 알고리즘과 유사한^{[clarification needed]} 다른 알고리즘은 때때로 "레버리징 알고리즘"^[9]이라고 불리기도 하지만 부스트 알고리즘이라고도 잘못 불리기도 한다.

많은 부스팅 알고리즘 사이의 주요 변동은 훈련 데이터 포인트와 가설을 가중화하는 방법이다.AdaBoost는 매우 인기 있고 역사적으로 가장 중요한 알고리즘으로 약한 학습자에게 적응할 수 있었다.그것은 종종 대학 기계 학습 ^[10]과정에서의 활성화에 대한 입문 보도의 기초가 된다.LPBoost, TotalBoost, BrownBoost, xgBoost, MadaBoost, LogitBoost 등의 최신 알고리즘이 많이 있습니다.많은 부스팅 알고리즘이 AnyBoost ^[9]프레임워크에 들어맞는데, 이는 부스팅이 볼록 비용 함수를 사용하여 함수 공간에서 경사 강하를 수행함을 보여줍니다.

컴퓨터 비전의 객체 분류

세계의 다양한 기존의 오브젝트를 포함한 화상이 주어지면, 분류자를 그것으로부터 학습해, 장래의 화상에서 오브젝트를 자동적으로 분류할 수 있다.개체의 일부 이미지 기능을 기반으로 작성된 단순 분류기는 분류 성능이 약한 경향이 있습니다.오브젝트 분류에 boost 메서드를 사용하는 것은 전체적인 분류 능력을 높이기 위해 취약한 분류자를 특별한 방법으로 통합하는 방법입니다.

객체 분류 문제

객체 분류는 이미지에 객체의 특정 범주가 포함되어 있는지 여부를 결정하는 컴퓨터 비전의 전형적인 작업입니다.이 아이디어는 인식, 식별 및 탐지와 밀접하게 관련되어 있습니다.외관 기반 객체 분류에는 일반적으로 기능 추출, 분류자 학습 및 분류자 새 예제에 적용이 포함됩니다.형상 분석, 단어 가방 모델 또는 SIFT와 같은 로컬 기술자 등 객체의 범주를 나타내는 방법은 여러 가지가 있습니다.감독 분류기의 예로는 Naigive Bayes 분류기, 서포트 벡터 머신, 가우시안 혼합 및 뉴럴 네트워크가 있습니다.그러나 연구에 따르면^[which?] 이미지에서 물체 범주와 그 위치가 감독되지 않은 방식으로 발견될 ^[11]수 있습니다.

객체 분류의 현상

이미지에서 객체 카테고리의 인식은 컴퓨터 비전에서 어려운 문제이며, 특히 카테고리 수가 많을 때는 더욱 그렇습니다.이는 클래스 내 변동성이 높고 동일한 범주 내의 개체 간에 일반화가 필요하기 때문입니다.한 범주 내의 개체는 상당히 다르게 보일 수 있습니다.같은 물체라도 다른 시점, 크기 및 조명 아래에서는 유사하지 않은 것으로 나타날 수 있습니다.배경의 혼란과 부분적인 폐색도 ^[12]인식의 어려움을 가중시킨다.인간은 수천 가지의 물체 유형을 인식할 수 있는 반면, 기존의 물체 인식 시스템은 대부분 사람의 얼굴, 자동차, 단순한 물체 ^{[13][needs update?]}등 몇 ^[quantify]가지만 인식하도록 훈련된다.연구는 더 많은 카테고리를 다루고 새로운 카테고리의 증분 추가를 가능하게 하는 데 매우 적극적이었으며, 일반적인 문제가 해결되지 않은 채로 남아 있지만, 여러 개의 다중 카테고리 물체 감지기(최대 수백 또는 수천 개의 카테고리^[14])가 개발되었다.한 가지 방법은 기능 공유와 증대를 통한 것입니다.

이진 분류를 위한 부스트

AdaBoost는 이진 분류의 예로 얼굴 감지에 사용할 수 있습니다.두 가지 범주는 얼굴 대 배경입니다.일반적인 알고리즘은 다음과 같습니다.

1. 다양한 심플한 기능 세트 형성
2. 교육용 이미지의 가중치 초기화
3. T라운드의 경우
   1. 가중치를 정규화하다
   2. 세트에서 사용 가능한 기능에 대해서는 단일 기능을 사용하여 분류자를 훈련하고 훈련 오류를 평가합니다.
   3. 오류가 가장 낮은 분류자를 선택합니다.
   4. 교육용 이미지의 가중치 업데이트: 이 분류기로 잘못 분류된 경우 증가, 올바르게 분류된 경우 감소
4. T 분류기의 선형 조합으로 최종 강 분류기를 형성한다(훈련 오류가 작을 경우 계수가 더 크다).

승압 후 200개의 기능으로 구성된 분류기는 10${\displaystyle {}^{}}$-$$(\$displaystyle$ 10$^{-5})$^[15]의 ${\displaystyle {\mathrm{거짓}}^{}}$ 양성률 하에서 95%의 검출률을 얻을 수 있다.

바이너리 분류를 위한 부스팅의 또 다른 적용은 움직임과 ^[16]외관 패턴을 이용하여 보행자를 감지하는 시스템이다.걷는 사람을 검출하는 기능으로서 동작 정보와 외관 정보를 조합한 것은 이 작품이 처음이다.Viola-Jones 물체 감지 프레임워크와 유사한 접근 방식을 취합니다.

다중 클래스 분류를 위한 상승

이진 분류와 비교하여 다중 클래스 분류는 범주 간에 동시에 공유할 수 있는 공통 기능을 찾습니다.기능처럼 일반적인 엣지가 됩니다.학습 중에 각 범주의 검출기를 공동으로 교육할 수 있습니다.개별 훈련에 비해 일반화가 더 잘 되고, 훈련 데이터가 더 적게 필요하며, 동일한 성능을 달성하기 위해 필요한 기능이 더 적습니다.

알고리즘의 주요 흐름은 바이너리 케이스와 유사합니다.다른 점은 공동 훈련 오류에 대한 측정이 사전에 정의되어야 한다는 것입니다.각 반복 중에 알고리즘은 단일 피쳐의 분류자를 선택한다(더 많은 카테고리에서 공유할 수 있는 피쳐는 권장된다).이는 멀티 클래스 분류를 바이너리 분류로 변환하거나(^[18]카테고리 세트 대 나머지)^[17] 분류기의 기능이 없는 카테고리에서 패널티 오류를 발생시킴으로써 수행할 수 있습니다.

논문 "멀티클래스 및 멀티뷰 객체 탐지를 위한 시각적 기능 공유"에서 A.토랄바 외는 GentleBoost를 부스팅에 사용하고, 트레이닝 데이터가 한정되어 있는 경우, 같은 부스팅 라운드에서 공유하지 않는 것보다 공유 기능을 통해 학습하는 것이 훨씬 낫다는 것을 보여주었습니다.또한 특정 성능 수준에 대해 특징 공유 검출기에 필요한 총 특징 수(따라서 분류기의 실행 시간 비용)는 클래스 수에 따라 대략적으로 로그로 스케일링되는 것으로 관찰된다. 즉, 비공유 사례의 선형 성장보다 느리다.유사한 결과는 "시각적 형태 알파벳을 사용한 물체 검출기의 증분 학습" 논문에서 나타나지만, 저자들은 부스팅을 위해 AdaBoost를 사용했다.

볼록 대 비볼록 부스트 알고리즘

부스트 알고리즘은 볼록 또는 비볼록 최적화 알고리즘에 기초할 수 있습니다.AdaBoost 및 LogitBoost와 같은 볼록 알고리즘은 약한 ^[19][20]가설의 기본적이고 학습 가능한 조합을 배울 수 없도록 랜덤 노이즈에 의해 "패배"될 수 있습니다.이 제한은 2008년 Long & Servedio에 의해 지적되었습니다.그러나 2009년까지 여러 저자들은 BrownBoost와 같은 비볼록 최적화에 기반한 알고리즘 부스팅이 잡음이 많은 데이터 집합에서 학습할 수 있으며 특히 롱 서비스 데이터 집합의 기본 분류자를 학습할 수 있다는 것을 입증했다.

「 」를 참조해 주세요.

실장

• Python용 오픈 소스 머신 러닝 라이브러리인 Scikit-learn
• Orange, 무료 데이터 마이닝 소프트웨어 스위트, 모듈 Orange.ensemble
• Weka는 AdaBoost 및 LogitBoost와 같은 부스트 알고리즘의 다양한 구현을 제공하는 기계 학습 도구 세트입니다.
• R 패키지 GBM(Generalized Boost Regression Models)은 Freund 및 Schapire의 AdaBoost 알고리즘과 Friedman의 그라데이션 부스트 기계에 대한 확장을 구현합니다.
• jBoost; AdaBoost, LogitBoost, RobustBoost, Boostexter 및 교대 Decision Tree
• R 패키지 adabag:멀티클래스 AdaBoost를 적용합니다.M1, AdaBoost-SAMME 및 배깅
• R 패키지 xgboost:선형 및 트리 기반 모델에 대한 그라데이션 부스트 구현.

메모들

레퍼런스

추가 정보

• 요브 프로인드와 로버트 E.Schapire(1997); 온라인 학습의 의사결정 이론 일반화와 컴퓨터 및 시스템 과학 저널, 55(1):119-139
• 로버트 E.Schapire and Yoram Singer(1999년);신뢰 등급 예측 변수를 사용한 향상된 부스트 알고리즘, 머신 러닝, 37(3): 297-336

외부 링크

• 로버트 E.Schapire(2003);머신 러닝을 촉진하는 접근법: 개요, MSRI(수학과학연구소)비선형 추정 및 분류 워크숍
• 저우즈화(2014) 25년 도약 CCL 2014 기조연설.
• Zhou, Zhihua (2008). "On the margin explanation of boosting algorithm" (PDF). In: Proceedings of the 21st Annual Conference on Learning Theory (COLT'08): 479–490.
• Zhou, Zhihua (2013). "On the doubt about margin explanation of boosting" (PDF). Artificial Intelligence. 203: 1–18. arXiv:1009.3613. doi:10.1016/j.artint.2013.07.002. S2CID 2828847.