과적합

Overfitting
시리즈의 일부
기계 학습
및 데이터 마이닝
Scatterplot featuring a linear support vector machine's decision boundary (dashed line)
문제
지도 학습
(분류 • 회귀)
클러스터링
치수 축소
구조화된 예측
이상 검출
인공신경망
강화 학습
인간과의 학습
모델 진단
이론.
기계학습장
관련 기사
그림 1녹색 선은 과적합 모형을 나타내고 검은색 선은 정규화된 모형을 나타냅니다.녹색 선은 교육 데이터를 가장 잘 따르지만, 해당 데이터에 너무 의존하여 검은색 선에 비해 보이지 않는 새로운 데이터에 대한 오류율이 높을 수 있습니다.
그림 2노이즈가 많은(대략 선형) 데이터가 선형 함수와 다항식 함수에 적합됩니다.다항식 함수는 완벽하지만 선형 함수는 더 잘 일반화될 것으로 예상할 수 있습니다. 두 함수를 사용하여 적합된 데이터를 초과하여 추정할 경우 선형 함수가 더 나은 예측을 할 수 있습니다.
그림 3파란색 점선은 언더핏 모델을 나타냅니다.직선은 포물선을 맞출 수 없다.이 모델은 너무 단순합니다.

수학적 모형화에서 과적합이란 "특정 데이터 집합에 너무 가깝거나 정확하게 일치하는 분석의 생성"을 말합니다. 따라서 추가 데이터에 적합하지 못하거나 미래의 [1]관측치를 안정적으로 예측하지 못할 수 있습니다.과적합 모형은 [2]데이터로 정당화할 수 있는 것보다 더 많은 모수를 포함하는 수학적 모형입니다.과적합의 본질은 마치 변동이 기본 모델 [3]: 45 구조를 나타내는 것처럼 잔류 변동(즉, 소음)의 일부를 무의식적으로 추출하는 것이다.

과소 적합은 수학적 모형이 데이터의 기본 구조를 적절하게 캡처할 수 없는 경우에 발생합니다.과소 적합 모형은 올바르게 지정된 모형에 나타나는 일부 모수 또는 항이 [2]결측된 모형입니다.예를 들어 비선형 데이터에 선형 모형을 적합시킬 때 과소 적합이 발생합니다.이러한 모델은 예측 성능이 떨어지는 경향이 있습니다.

모형을 선택하는 데 사용되는 기준이 모형의 적합성을 판단하는 데 사용되는 기준과 동일하지 않기 때문에 과적합 가능성이 있습니다.예를 들어, 모델은 일부 교육 데이터에 대한 성능을 극대화하여 선택될 수 있지만, 그 적합성은 보이지 않는 데이터에 대해 잘 수행할 수 있는 능력에 따라 결정될 수 있습니다. 그런 다음 모델이 추세에서 일반화하기 위해 교육 데이터를 "학습"하는 것이 아니라 "기억"하기 시작할 때 과다 적합이 발생합니다.

극단적인 예로서 모수의 수가 관측치 수와 같거나 클 경우, 모형은 데이터 전체를 암기하는 것만으로 훈련 데이터를 완벽하게 예측할 수 있습니다(그림 2 참조).그러나 이러한 모델은 일반적으로 예측을 할 때 심각하게 실패한다.

과적합 가능성은 모수와 데이터의 수뿐만 아니라 모형 구조의 데이터 형태 적합성 및 [citation needed]데이터의 예상되는 잡음 또는 오류 수준과 비교한 모형 오류의 크기에 따라 달라집니다.적합 모형에 과도한 수의 모수가 없는 경우에도 적합 관계가 적합에 사용되는 데이터 집합([2]수축이라고도 하는 현상)보다 새 데이터 집합에서 성능이 저하될 것으로 예상됩니다.특히, 결정 계수의 값은 원래 데이터에 비해 축소됩니다.

과적합 가능성 또는 양을 줄이기 위해 몇 가지 기법(예: 모델 비교, 교차 검증, 정규화, 조기 정지, 가지치기, 베이지안 사전 또는 드롭아웃)을 사용할 수 있습니다.일부 기법의 기초는 (1) 지나치게 복잡한 모델에 명시적으로 불이익을 주거나 (2) 훈련에 사용되지 않는 데이터 집합에 대한 성능을 평가하여 일반화하는 모델의 능력을 테스트하는 것이다. 이는 모델이 직면하게 될 전형적인 보이지 않는 데이터에 근접하는 것으로 가정한다.

통계적 추론

통계학에서, 추론은 어떤 절차를 통해 선택된 통계 모델로부터 도출된다.Burnham & Anderson은 모델 선정에 대해 많이 인용된 텍스트에서 과적합을 피하기 위해 "절약 원칙"[3]을 고수해야 한다고 주장한다.저자들은 또한 다음과 같이 말하고 있다.[3]: 32–33

과적합 모델은 파라미터 추정치에 편중되어 있지 않은 경우가 많지만, 불필요하게 큰 샘플링 분산을 추정(및 실제)하는 경우가 많습니다(추정기의 정밀도는 보다 인색한 모델로 달성할 수 있었던 것에 비해 저하).잘못된 치료 효과는 식별되는 경향이 있으며 잘못된 변수는 과다 적합 모형에 포함됩니다.…최적의 근사 모델은 언더피팅과 오버피팅의 오차를 적절히 조정함으로써 달성됩니다.

분석을 안내할 수 있는 이론이 거의 없는 경우 과적합이 심각한 문제가 될 가능성이 높으며, 이는 부분적으로 선택할 수 있는 모델이 많은 경향이 있기 때문입니다.Model Selection and Model Averaging (2008)이라는 책은 이렇게 [4]표현하고 있습니다.

데이터 세트를 지정하면 버튼 한 번으로 수천 개의 모델을 장착할 수 있지만, 최적의 모델을 선택하려면 어떻게 해야 할까요?후보 모델이 너무 많아서 과적합은 정말 위험합니다.햄릿을 타이핑한 원숭이가 정말 좋은 작가인가요?

회귀

회귀 분석에서 과적합이 [5]자주 발생합니다.극단적인 예로, 데이터 점이 p개인 선형 회귀 분석에서 p개의 변수가 있는 경우 적합선은 모든 [6]점을 정확히 통과할 수 있습니다.로지스틱 회귀 분석 또는 콕스 비례 위험 모델의 경우 다양한 경험 규칙이 있다(예: 5-9,[7] 10[8] 및 10-15[9] - 독립 변수당 10개 관측치의 지침은 "10개 중 하나"로 알려져 있다).회귀 모형을 선택하는 과정에서 랜덤 회귀 함수의 평균 제곱 오차는 회귀 함수의 추정에서 랜덤 노이즈, 근사 바이어스 및 분산으로 나눌 수 있습니다.치우침-분산 트레이드오프는 종종 과적합 모형을 극복하는 데 사용됩니다.

실제로 종속 변수와 관련이 없는 많은 설명 변수 집합이 예측되면, 일반적으로 일부 변수가 통계적으로 유의한 것으로 잘못 확인되고 연구자가 이를 모형에 유지하여 모형을 과적합시킬 수 있습니다.이것은 프리맨의 역설로 알려져 있다.

기계 학습

그림 4감독된 학습(예: 뉴럴 네트워크)에서의 과적합/과잉 훈련.교육 오류는 파란색으로 표시되고 검증 오류는 빨간색으로 표시됩니다. 이 두 오류는 모두 교육 주기 수에 따른 함수입니다.검증 오차는 증가하는 반면(양수 기울기) 교육 오차는 꾸준히 감소하는(음수 기울기) 경우 과적합 상태가 발생한 것일 수 있습니다.최적의 예측 및 적합 모형은 검증 오차가 전역 최소값을 갖는 모형입니다.

통상, 학습 알고리즘은, 「훈련 데이터」의 세트를 사용해 트레이닝 됩니다.즉, 원하는 출력을 알 수 있는 예시적인 상황입니다.목표는 알고리즘이 훈련 중에 발생하지 않은 "검증 데이터"를 제공받았을 때 출력을 예측하는 데도 잘 수행된다는 것입니다.

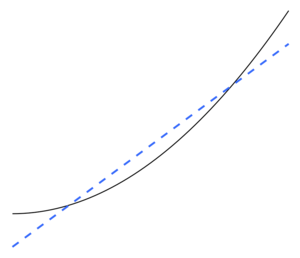
과적합이란 Occam의 면도기를 위반하는 모델 또는 절차를 사용하는 것입니다. 예를 들어, 궁극적으로 최적인 것보다 더 많은 조정 가능한 매개 변수를 포함하거나 궁극적으로 최적인 것보다 더 복잡한 접근 방식을 사용하는 것입니다.조정 가능한 매개 변수가 너무 많은 예에서는 두 독립 변수의 선형 함수를 통해 y에 대한 교육 데이터를 적절하게 예측할 수 있는 데이터 집합을 고려하십시오.이러한 함수에는 세 개의 매개변수(절편 및 두 개의 기울기)만 필요합니다.이 간단한 함수를 보다 복잡한 새로운 2차 함수로 대체하거나 두 개 이상의 독립 변수에서 보다 복잡한 새로운 선형 함수로 대체하면 다음과 같은 위험이 따릅니다.Occam의 면도기는 주어진 복잡한 함수는 주어진 단순한 함수보다 가능성이 낮다는 것을 의미합니다.단순함수 대신 새롭고 복잡한 함수가 선택되고 복잡성 증가를 상쇄하기에 충분한 훈련 데이터 적합성이 확보되지 않은 경우, 새로운 복합 함수는 데이터를 "과잉"하고 복잡한 오버핏 함수는 외부 검증 데이터에 대한 단순한 함수보다 더 나쁜 성능을 발휘할 가능성이 높습니다.복잡한 기능이 교육 데이터 [10]집합에서도 수행되거나 더 나은 수행이 가능하더라도 교육 데이터 집합에서 수행될 수 있습니다.

여러 유형의 모형을 비교할 때 각 모형에 있는 모수의 수를 세는 것만으로 복잡성을 측정할 수 없습니다. 각 모수의 표현성도 고려해야 합니다.예를 들어, m개의 매개변수를 가진 (곡선 관계를 추적할 수 있는) 신경망의 복잡성을 n개의 [10]매개변수를 가진 회귀 모델에 직접 비교하는 것은 중요하지 않다.

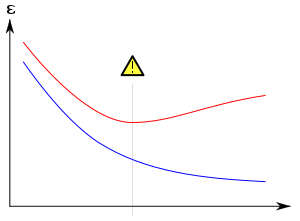
과적합은 학습이 너무 오래 수행되거나 훈련 예가 드문 경우에 특히 발생하며, 이로 인해 학습자는 목표 기능과 인과 관계가 없는 훈련 데이터의 매우 특정한 무작위 특징에 적응할 수 있다.이 과적합 프로세스에서는 교육 예제의 성능은 계속 향상되지만 보이지 않는 데이터의 성능은 저하됩니다.

간단한 예로, 구입한 품목, 구매자 및 구매 날짜와 시간을 포함하는 소매 구매 데이터베이스를 고려하십시오.구입일시를 사용하여 다른 속성을 예측함으로써 트레이닝 세트에 딱 맞는 모델을 쉽게 구축할 수 있지만, 이 모델은 새로운 데이터로 일반화되지 않습니다.이는 과거의 시간이 다시는 발생하지 않기 때문입니다.

일반적으로 학습 알고리즘은 알려진 데이터에 더 정확하지만(힌사이트), 새로운 데이터 예측에 더 정확하지 않으면(선견지명) 단순한 알고리즘에 비해 과적합한다고 한다.과거의 모든 경험에서 얻은 정보는 미래와 관련된 정보와 무관한 정보("노이즈")라는 두 가지 그룹으로 나눌 수 있다는 사실에서 과적합성을 직관적으로 이해할 수 있다.다른 모든 것이 동일할 경우, 기준이 예측하기 어려울수록(즉, 불확실성이 높을수록), 무시해야 할 과거 정보에 더 많은 소음이 존재한다.문제는 어느 부분을 무시할지를 결정하는 것입니다.소음의 위험을 줄일 수 있는 학습 알고리즘은 "강력"이라고 불립니다.

결과들

과적합으로 인한 가장 명백한 결과는 검증 데이터 세트의 성능 저하입니다.기타 부정적인 결과는 다음과 같습니다.[10]

  • 오버핏된 기능은 검증 데이터 세트의 각 항목에 대해 최적의 기능보다 더 많은 정보를 요구할 수 있습니다. 특히 각 개별 정보를 사람의 관찰 및 수동 데이터 입력에 의해 수집해야 하는 경우, 이 추가 불필요한 데이터를 수집하려면 비용이 많이 들거나 오류가 발생하기 쉽습니다.
  • 더 복잡하고 지나치게 적합한 기능은 단순한 기능보다 휴대성이 떨어질 수 있습니다.극단적으로 1변수 선형 회귀는 매우 휴대성이 뛰어나 필요하면 손으로도 수행할 수 있습니다.또 다른 극단적인 예로는 원래 모델러의 전체 설정을 정확하게 복제하여 재사용 또는 과학적 재현을 어렵게 만드는 것만으로 재현할 수 있는 모델이 있습니다.

구제책

최적의 기능을 위해서는 일반적으로 더 크거나 완전히 새로운 데이터 세트에 대한 검증이 필요합니다.단, 상관계수와 시계열(윈도 폭)의 의존성을 적용하는 최소 스패닝트리 또는 상관수명 등의 방법이 있습니다.창 너비가 충분히 클 때마다 상관 계수는 안정적이며 창 너비 크기에 더 이상 의존하지 않습니다.따라서 조사된 변수 간의 상관 계수를 계산하여 상관 행렬을 생성할 수 있습니다.이 행렬은 변수 간의 직접적 및 간접적 영향을 시각화하는 복잡한 네트워크로 위상적으로 표현될 수 있다.드롭아웃 정규화는 또한 견고성을 개선하여 레이어에 대한 입력을 확률적으로 제거함으로써 과적합을 줄일 수 있다.

언더피팅

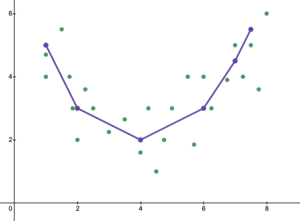
그림 5빨간색 선은 파란색으로 표시된 데이터 점의 과소 적합 모형을 나타냅니다.데이터 점의 곡률을 나타내는 포물선 모양의 선을 볼 수 있을 것입니다.
그림 6파란색 선은 녹색으로 표시된 데이터 점의 적합 모형을 나타냅니다.

과소 적합은 과적합의 역순으로, 통계 모형 또는 기계 학습 알고리즘이 너무 단순하여 데이터를 정확하게 나타낼 수 없습니다.과소 적합의 징후는 사용된 현재 모형 또는 알고리즘에서 높은 치우침과 낮은 분산이 감지된다는 것입니다(과적합의 역수: 낮은 치우침과 높은 분산).이는 바이어스 오차, 분산 오차 및 환원 불가능한 오차에 대한 모델 또는 알고리즘을 분석하는 방법인 바이어스-분산 트레이드오프에서 수집할 수 있습니다.치우침이 크고 분산이 적을 경우 모형의 결과는 데이터 점을 부정확하게 나타내므로 미래의 데이터 결과를 충분히 예측할 수 없습니다(일반화 오류 참조).그림 5에 나타난 것처럼, 점의 곡률과 유사하지 않은 선으로 인해 선형 선은 주어진 모든 데이터 점을 나타낼 수 없었다.그림 6과 그림 1과 같이 포물선 모양의 선이 나타날 것으로 예상됩니다.앞에서 설명한 바와 같이 그림 5를 분석에 사용할 경우 그림 6을 분석하면 결과와 달리 잘못된 예측 결과를 얻을 수 있습니다.

Burnham & Anderson은 다음과 [3]: 32 같이 진술합니다.

…적합된 모델은 데이터 내의 중요한 복제 가능 구조(즉, 대부분의 다른 샘플에서 개념적으로 복제 가능)를 무시하기 때문에 실제로 데이터에 의해 지원되는 효과를 식별할 수 없습니다.이 경우 모수 추정기의 편향이 상당하며 표본 분산이 과소평가되어 두 요인 모두 신뢰 구간 커버리지가 저하됩니다.과소 적합 모형은 실험 환경에서 중요한 처리 효과를 놓치는 경향이 있습니다.

언더피팅 해결

언더피팅 해결은 여러 가지 방법으로 처리할 수 있으며, 가능한 방법은 모형의 모수를 늘리거나 더 많은 교육 데이터를 추가하는 것입니다.트레이닝 데이터의 추가는, 현재의 기능(기능 엔지니어링이라고 불린다)으로부터 새로운 기능을 취득하는 것으로 실시할 수 있습니다.또 다른 가능한 방법은 현재의 통계 모델 또는 기계 학습 알고리즘에서 데이터를 더 잘 나타낼 수 있는 다른 알고리즘으로 이동하는 것이다.

「 」를 참조해 주세요.

메모들

  1. ^ OxfordDictionaries.com에서 "과잉 적합"에 대한 정의: 이 정의는 특히 통계를 위한 것입니다.
  2. ^ a b c Everitt B.S., Scrondal A. (2010), 케임브리지 통계 사전, 케임브리지 대학 출판부.
  3. ^ a b c d 를 클릭합니다Burnham, K. P.; Anderson, D. R. (2002), Model Selection and Multimodel Inference (2nd ed.), Springer-Verlag.
  4. ^ 를 클릭합니다Claeskens, G.; Hjort, N.L. (2008), Model Selection and Model Averaging, Cambridge University Press.
  5. ^ 를 클릭합니다Harrell, F. E., Jr. (2001), Regression Modeling Strategies, Springer.
  6. ^ Martha K. Smith (2014-06-13). "Overfitting". University of Texas at Austin. Retrieved 2016-07-31.
  7. ^ Vittinghoff, E.; McCulloch, C. E. (2007). "Relaxing the Rule of Ten Events per Variable in Logistic and Cox Regression". American Journal of Epidemiology. 165 (6): 710–718. doi:10.1093/aje/kwk052. PMID 17182981.
  8. ^ Draper, Norman R.; Smith, Harry (1998). Applied Regression Analysis (3rd ed.). Wiley. ISBN 978-0471170822.
  9. ^ Jim Frost (2015-09-03). "The Danger of Overfitting Regression Models". Retrieved 2016-07-31.
  10. ^ a b c Hawkins, Douglas M (2004). "The problem of overfitting". Journal of Chemical Information and Modeling. 44 (1): 1–12. doi:10.1021/ci0342472. PMID 14741005.

레퍼런스

추가 정보

외부 링크