S그모이드 함수

시리즈의 일부
기계 학습 및 데이터 마이닝
문제 분류 클러스터링 회귀 이상 검출 데이터 클리닝 자동 ML 어소시에이션 규칙 강화 학습 구조화된 예측 기능 엔지니어링 기능 학습 온라인 학습 준지도 학습 비지도 학습 순위 매기기 학습 문법 유도
지도 학습 (분류 • 회귀) 의사결정 트리 앙상블 배깅 부스팅 랜덤 포레스트 k-NN 선형 회귀 네이비 베이즈 인공신경망 로지스틱 회귀 분석 퍼셉트론 관련 벡터 머신(RVM) 서포트 벡터 머신(SVM)
클러스터링 버치 치유하다 계층적 k자형 기대 최대화(EM) DBSCAN 광학 평균 이동
치수 축소 인자 분석 CCA ICA LDA NMF PCA PGD t-SNE
구조화된 예측 그래픽 모델 베이즈 네트 조건부 랜덤 필드 히든 마르코프
이상 검출 k-NN 국소 특이치 계수
인공신경망 자동 인코더 인지 컴퓨팅 딥 러닝 딥 드림 다층 퍼셉트론 RNN LSTM GRU ESN 저장고 계산 제한 볼츠만 기계 GAN somerset. 컨볼루션 뉴럴 네트워크 유넷 트랜스포머 비전. 스파이킹 뉴럴 네트워크 메모리 트랜지스터 전기화학 RAM(ECRAM)
강화 학습 Q-러닝 사사 시간차(TD) 멀티 에이전트 셀프 플레이
인간과의 학습 액티브 러닝 크라우드 소싱 휴먼 인 더 루프
모델 진단 학습 곡선
이론. 커널 머신 바이어스-분산 트레이드오프 컴퓨터 학습 이론 경험적 리스크 최소화 오컴 러닝 PAC 학습 통계학 학습 VC 이론
기계학습장 NeurolIPS ICML ML JMLR ArXiv:cs.LG
관련 기사 인공지능 용어집 기계 학습 연구를 위한 데이터 세트 목록 기계학습의 개요
v t

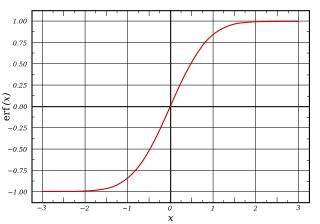
S자형 함수는 특징적인 S자형 곡선 또는 S자형 곡선을 갖는 수학 함수이다.

Sigmoid 함수의 일반적인 예는 첫 번째 그림에 나타나며 다음 ^[1]공식으로 정의되는 로지스틱 함수입니다.

$({displaystyle S(x)=param frac {1}{1+e^{-x}}=param frac {e^{x}}{e^{x}+1}=1-S(-x)}).$

기타 표준 Sigmoid 함수는 예제 섹션에 나와 있습니다.일부 분야에서, 특히 인공 신경망의 맥락에서, "sigmoid 함수"라는 용어는 로지스틱 함수의 별칭으로 사용됩니다.

Sigmoid 함수의 특별한 경우로는 Gompertz 곡선(x의 큰 값으로 포화되는 모델링 시스템에 사용됨)과 Oge 곡선(일부 댐의 여수로에 사용됨)이 있습니다.Sigmoid 함수는 모든 실수의 도메인을 가지며, 리턴(응답) 값은 일반적으로 단조롭게 증가하지만 감소할 수 있습니다.Sigmoid 함수는 대부분 0 ~1 범위의 반환값(y축)을 표시합니다.일반적으로 사용되는 다른 범위는 -1 ~1 입니다.

로지스틱 함수와 쌍곡선 탄젠트 함수를 포함한 다양한 S자형 함수가 인공 뉴런의 활성화 함수로 사용되어 왔다.Sigmoid 곡선은 로지스틱 밀도의 적분, 정규 밀도 및 Student의 t 확률 밀도 함수와 같은 누적 분포 함수(0부터 1)로도 일반적입니다.로지스틱 Sigmoid 함수는 반전 가능하며, 그 역함수는 로짓 함수입니다.

정의.

Sigmoid 함수는 모든 실제 입력 값에 대해 정의되며 각 점^[1] 및 정확히 하나의 변곡점에 음이 아닌 도함수를 갖는 유계 미분 가능한 실제 함수입니다.S자형 "함수"와 S자형 "곡선"은 같은 물체를 가리킨다.

특성.

일반적으로 S자 함수는 단조롭고 종 모양의 제1도함수를 가진다.반대로, 음이 아닌 연속적인 벨 모양의 함수(퇴화되지 않는 한 로컬 최대값은 1개이고 로컬 최소값은 없음)의 적분은 S자형이 됩니다.따라서 많은 공통 확률 분포에 대한 누적 분포 함수는 S자형입니다.이러한 예 중 하나는 정규 분포의 누적 분포 함수와 관련된 오차 함수이고, 다른 하나는 코시 분포의 누적 분포 함수와 관련된 아크탄 함수입니다.

Sigmoid 함수는 수평 점근 쌍에 의해 x ${\displaystyle \to }$ ± ${\$ { $displaystyle$ x$\rightarrow \pm \infty$ $\}$로 구속된다.

Sigmoid 함수는 특정 점보다 작은 값에는 볼록하고, 그 점보다 큰 값에는 오목하다.여기서 많은 예에서 그 점은 0이다.

예

• 로지스틱 함수
  $${\displaystyle f(x)=syslogfrac {1}{1+e^{-x}}}}$$

  
• 쌍곡선 탄젠트(위의 로지스틱 함수의 이동 및 축소 버전)
  $${\displaystyle f(x)=\tanh x=subscfrac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}$$

  
• 아크탄젠트 함수
  $${\displaystyle f(x)=\arctan x}$$

  
• 구더만 함수
  $${\displaystyle f(x)=\operatorname {gd}(x)=\int _{0}^{x}{\frac {dt}{\cosh t}=2\arctan \left(\tanh \frac {x}{x}\right)}$$

  
• 오류 함수
  $${\displaystyle f(x)=\operatorname {erf}(x)=pic frac {2}{\displayrt {pi }}\int _{0}^{x}e^{-t^{2}},dt}$$

  
• 일반화 로지스틱 함수
  $$\displaystyle f(x)=\left(1+e^{-x}\오른쪽)^{-\alpha},\displaystyle \alpha >0}$$

  
• 스무스 스텝 기능
  $${\displaystyle f(x)=flash {case}{\displaystyle \left(\int _{0}^1}\left(1-u^{2}\right)^{N}du\right)^{-1}\int _{0}^{x}\left(1-u^{2}\right)^{N}\du}, & x \leq 1\\\operatorname {sgn}(x) & x \geq 1\\end {case}\quad N\in \mathbb {Z} \geq 1)$$

  
• 예를 들어 몇 가지 대수함수
  $${\displaystyle f(x)=paramfrac {x}{\paramrt {1+x^{2}}}}}}$$

  
• 그리고 좀 더^[2] 일반적인 형태로
  $${\displaystyle f(x)=flac {x}{\left(1+x^{k}\오른쪽)^{1/k}}}}$$

  
• 시프트와 스케일링에 이르기까지 많은 S자형이 특별한 경우입니다.
  $$(\displaystyle f(x)=\varphi (\varphi (x,\varphi),\alpha ) )$$

  
  어디에
  $${\displaystyle \varphi (x,\displayda )=display{cases}(1-\displayda x)^1/\displayda }&\displayda \neq 0\e^{-x}&\displayda = 0\end{cases}$$

  
  는 음의 Box-Cox 변환의 이며 α < \ $displaystyle \alpha < 1$ >β < \ $displaystyle \beta < 1$}는 형상 파라미터입니다.^[3]

적용들

복잡한 시스템 학습 곡선과 같은 많은 자연적 과정은 시간이 지남에 따라 가속화되고 정점에 도달하는 작은 시작부터의 진전을 보인다.특정한 수학적 모델이 없을 때, 종종 ^[4]S자형 함수가 사용된다.

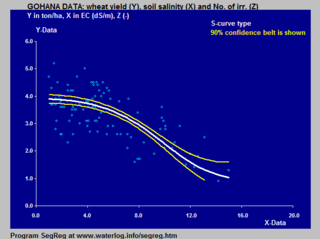
반 진헨-굽타 모델은 역 S 곡선을 기반으로 하며 토양 염도에 대한 농작물 수확량 반응에 적용된다.

로지스틱 S곡선의 토양 염도 및 토양 내 수분표에 대한 깊이에 대한 작물 수확량(밀) 반응에 대한 적용 예는 로지스틱 함수 #에 나와 있다.농업: 작물의 반응을 모델링합니다.

인공신경망에서는 효율을 위해 평활하지 않은 기능이 대신 사용되기도 합니다.이것들을 하드 시그모이드라고 합니다.

오디오 신호 처리에서는 아날로그 회로 ^[5]클리핑의 소리를 에뮬레이트하기 위한 도파 전사 함수로 S자형 함수를 이용한다.

생화학 및 약리학에서 힐 방정식과 힐-랑뮤르 방정식은 S자형 함수이다.

컴퓨터 그래픽스 및 실시간 렌더링에서 일부 Sigmoid 함수는 두 값 사이에 색상 또는 지오메트리를 부드럽게 혼합하기 위해 사용됩니다.

강산과 강염기 사이의 적정곡선은 pH 척도의 대수적 성질에 의해 S자형이다.

로지스틱 함수는 유형 III ^[6]우넘을 사용하여 효율적으로 계산할 수 있습니다.

「 」를 참조해 주세요.

레퍼런스

추가 정보

• 미첼, 톰은 M.(1997년).기계 학습.WCB McGraw–Hill.아이 에스비엔 978-0-07-042807-2.. 미첼. 그는 또한"기능 꼴짝 꼴짝"–고 S자(군수aka)기능은"뉴런"의 출력 압축하는 데 사용한 부른다 이 기능 – 그 단어"기능 군수"과"시그모이드 함수"을 사용한다(NB다. 특히 특히았지만"4장:인공 신경망을 이용한"(를 대신하여 서명함. 96–97). 다층 신경 ne에ts)
• Humphrys, Mark. "Continuous output, the sigmoid function". Archived from the original on 2022-07-14. Retrieved 2022-07-14. (NB. Sigmoid의 특성. 축을 따라 이동하는 방법 및 영역을 변환하는 방법을 포함합니다.)

외부 링크

• S 곡선을 데이터 세트에 적합시키는 소프트웨어