atan2

The function ${\displaystyle \operatorname {atan2} (y,x)}$ or ${\displaystyle \operatorname {arctan2} (y,x)}$ (from "2-argument arctangent") is defined as the angle in the Euclidean plane, given in radians, between the positive x axis and the ray to the point (x, y) ≠ (0, 0).

${\displaystyle \mathrm{atan2}}$ ${\displaystyle }$(${\displaystyle y}$, ${\displaystyle x}$) ${\displaystyle \operatorname {atan2}(y,x)}$은(는) 프로그래밍 언어 Fortran에 처음$$ 나타났다(IBM의 1961년 구현 FORTRAN-IV에서). 원래는 데카르트 좌표(x, y)에서 극좌표(r, θ)로 변환할 때 각 θ에 대한 정확하고 모호하지 않은 값을 반환하기 위한 것이었다.

마찬가지로 ${\displaystyle \mathrm{atan2}}$ ${\displaystyle (y}$, x )${\displaystyle \operatorname {atan2}(y,x)}$은 복합 숫자 $x{\displaystyle }$+ ${\displaystyle i}$ ${\displaystyle y}$ .${\displaysty x+iy$의 인수(단계 또는 각도라고도 함)이다$.$$}$

${\displaystyle \mathrm{atan2}}$ ${\displaystyle }$(${\displaystyle y}$, x${\displaystyle }$) ${\displaystyle \operatorname {atan2}(y,x)}$은(는) -π < ≤ ≤ π π, 일부 r > 0과 같은 단일 값 θ을 반환한다$$.

${\displaystyle {\displaysty}x&=r\cos \theta,\y&=r\sin \theta .\ended}}}$

$r$= $\sqrt{{x\mathrm{}}^{}}$ 2$\sqrt{{}^{}}$+ y $\sqrt{{2\mathrm{}}^{}}$ ${\$}는 사실이지만$\}\}\}\},$ 다음과 같은 동등성이 항상 유지되는 것은 아니다.

${\displaystyle \theta =\arctan \leftfrac\frac {y}{x}\오른쪽).}$

이것은 x > 0일 때만 지탱된다. x < 0일 때, 위의 표현에서 보이는 각도는 정확한 각도의 반대 방향을 가리키며, π (또는 180°)의 값을 가리킨다. 카르트 점(x, y)을 유클리드 평면의 정확한 사분면에 넣으려면 θ에서 추가하거나 빼야 한다.^[1] 이를 위해서는 x와 y의 기호를 별도로 알아야 하는데, y를 x로 나누면 잃어버린다.

2㎛의 정수배수는 x나 y를 변경하지 않고 θ 각도에 추가할 수 있기 때문에 반환된 값에 대한 모호한 값을 의미하므로 (좌측 개방, 우측 폐쇄) 간격(- angle, π)에서 각도의 주값이 반환된다. θ이 서명되며, 반시계각은 양의 각, 시계방향은 음의 각이다. 즉, ${\displaystyle \mathrm{atan2}}$ ${\displaystyle }$(${\displaystyle y}$, ${\displaystyle x}$)$${\$displaystyle \operatorname {atan2}(y,x)}$은(는) 닫힌 간격[0, ]]에 있고, y가 0일 때는 열린 간격(-π, 0)에 있다.

역사와 동기

atan2 기능은 컴퓨터 프로그래밍 언어에 처음 도입되었지만, 지금은 다른 이공계 분야에서도 흔히 볼 수 있다. 그것은 적어도 FORTRAN 프로그래밍 언어까지^[2] 거슬러 올라가고 있으며, 현재 많은 현대 프로그래밍 언어에서 발견되고 있다. 이러한 언어로는 C의 math.hstandard 라이브러리, Java math 라이브러리 등이 있다.NET의 시스템.수학(C#, VB에서 사용 가능)NET 등), 파이썬 수학 모듈, 루비 수학 모듈, 바둑 수학 패키지^[3] 등. 또한 Perl과 같은 많은 스크립팅 언어에는 C-style이 포함된다. atan2(y, x) 기능을 발휘하다

단개론 아크탄젠트 함수는 정반대의 방향을 구별할 수 없다. 예를 들어, 아크탄(1/1)으로 통상적인 방법으로 계산한 x축에서 벡터(1, 1)까지의 반시계방향 각도는 π/4(라디안) 또는 45°이다. 단, x축과 벡터(-1, -1) 사이의 각도는 같은 방법으로 아크탄(-1/-1)으로 나타나며, 답은 -34/4(-135°)로 예상할 수 있지만, 다시 π/4로 나타난다. 또는 5°/4° 또한 x축과 벡터(0, y), y ≠ 0 사이의 각도를 찾으려면 아크탄(y/0)의 평가가 필요하며, 이 값은 0으로 분할할 때 실패한다.

atan2 함수는 두 변수 y와 x에서 하나의 고유한 호 접선 값을 계산하는데, 여기서 두 변수의 부호가 모두 결과의 사분원을 결정하는 데 사용되어, 예를 들어 atan2(1, 1) = //4 및 atan2(-1, -1) = -3//4의 원호 접선의 가지를 선택한다. 마찬가지로, 예: atan2(1, 0) = =/2.

계산을 수동으로 할 때는 필요한 사분면 수정과 예외 처리를 검사로 할 수 있지만, 항상 모호하지 않은 정확한 결과를 주는 단일 기능을 갖는 것이 더 유용하다. atan2 함수는 한 지점에서 다른 지점으로 방향을 찾는 것과 같이 유클리드 공간의 벡터를 포함하는 많은 응용에서 유용하다. 회전 행렬 표현을 오일러 각도로 변환하기 위해 컴퓨터 그래픽 회전에 주로 사용된다.

역사적 발언

1966년 FORTRAN 사람들은 (x,y)-카르테시아 평야를 다루는데 의심의 여지가 없고 +x 축이 모든 (x,y)-논란이 0을 산출하기 위한 의도라는 점에서 소위 극축의 두드러진 역할을 하지만 논쟁의 순서(y,x)를 선택했다. 아마도 그들의 선택은 똑같이 xy를⁻¹ 잘 생각할 수 있었지만, 대부분 y/x라는 몫의 순서를 연상시키는 것일 것이다.

정의 및 계산

atan2 함수는 복합수 x + yi에 적용된 인수함수의 주값을 계산한다. 즉, atan2(y, x) = Pr arg(x + i) = Arg(x + i)이다. 인수는 각도에 아무런 차이를 두지 않고 임의의 배수로 2㎛(원점을 완전히 도는 것에 대응함)에 의해 변경될 수 있지만, atan2를 고유하게 정의하기 위해서는 범위(${\displaystyle }$- ${\displaystyle \pi }$ , ${\displaystyle \pi }$ ${\displaystyle ]}$의 주값을 사용한다( - π${\displaystyle ,}$π,$]$ ] ], at at at$).$

표준 아크탄 함수의 경우 범위가 (-π/2, π/2)인 경우 다음과 같이 표현할 수 있다.

${\displaystyle \operatorname{atan2}(y,x)=ᆭ\arctan({\frac{y}{x}})&,{\text{만약}}x>, 0,\\\arctan({\frac{y}{x}})+\pi&{\text{만약}}x<, 0{\text{과}}y\geq 0,\\\arctan({\frac{y}{x}})-\pi&{\text{만약}}x<, 0{\text{과}}y<, 0,\\+{\frac{\pi}{2}}&{\text{만약}}x=0{\text{과}}y>, 0,\\-{\frac{\pi}{2}}&{\text{만약}.}x=0{\text{과}}y<, 0,\\{\text{물결 모양의farget}&{\text{}}}}{x=0{\text{ 및 }}}}y=0.\end{case}}}$

4개의 겹치는 하프플레인이 있는 콤팩트한 표현은

${\displaystyle \operatorname{atan2}(y,x)={\begin{경우}\arctan \left({\frac{y}{x}}\right)&,{\text{만약}}x>, 0,\\{\frac{\pi}{2}}-\arctan \left({\frac{x}{y}}\right)&,{\text{만약}}y>, 0,\\-{\frac{\pi}{2}}-\arctan \left({\frac{x}{y}}\right)&,{\text{만약}}y<, 0,\\\arctan \left({\frac{y}{x}}\right)\pm\pi&{\text{만약}}x<, 0,\\{\te.xt{한정되지 않은}}&{\text{만약}})=0{\text{ 및 }}y=0.\end{case}}}$

Iverson 괄호 표기법은 훨씬 더 압축적인 표현을 허용한다.

명백한 조건부 구문이 없는 공식:

${\displaystyle \operatorname {atan2} (y,x)=\operatorname {sgn}(x)^{2}\arctan \left({\frac {y}{x}}\right)+{\frac {1-\operatorname {sgn}(x)}{2}}\left(1+\operatorname {sgn}(y)-\operatorname {sgn}(y)^{2}\right)\pi }$

접선 반각 공식에서 도출한 다음 식도 atan2를 정의하는 데 사용할 수 있다.

${\displaystyle \propertname {atan2}(y,x)={\case}2\arctan \leftder\fractan {y}{\sqrt {x^{x^{2}+y^{2}}}}+x}}\오른쪽)&#{{\x}0{\x}{{\x}{{\neq 0,\\\pi &{\\cext}}}}}}}}}}}}}}}}}{x=0}{\text={\cext{}}}, }}}x={\cext}}}}.\end{case}}}$

이 표현은 위의 정의보다 상징적인 용도에 더 적합할 수 있다. 그러나 x ${\displaystyle \sqrt{{2\mathrm{}}^{}}}$+ y ${\displaystyle \sqrt{{2\mathrm{}}^{}}}$ ${\$}의 반올림 오류의 효과가 있으므로 일반적인 부동 소수점 계산 용도에 적합하지 않다.$}}}}$ 지역 근처로 확장$$ x < 0, y = 0(이는 y를 0으로 나눌 수도 있음)

이러한 팽창된 라운딩 오류를 방지하는 마지막 공식의 변형:

${\displaystyle \propertname {atan2}(y,x)={\case}2\arctan \leftder\fractan {y}{\sqrt {x^{x^{2}+y^{2}}}}+x}}\right)&{\text{if }}x>0,\\2\arctan \left({\frac {{\sqrt {x^{2}+y^{2}}}-x}{y}}\right)&{\text{if }}x\leq 0{\text{ and }}y\neq 0,\\\pi &{\text{if }}x<0{\text{ and }}y=0,\\{\text{undefined}}&{\text{if }}x=0{\text{ and }}y=0.\end{case}}}$

주의:

• 이것은 (- (-, π)^{[note 2]} 범위의 결과를 산출한다.
• 위에서 언급한 바와 같이 atan2(y, x) 인수의 기본값은 삼각측정에 의한 아크탄(y/x)과 관련될 수 있다. 그 유래는 다음과 같다.

(x, y) = (r cos θ, r sin θ)이면 태닝((θ/2) = y / (r + x) 그 뒤를 잇는다.

${\displaystyle {\textan2}}(y,x)=\theta =2\,\theta /2=2\arctan {\fract {y}{\sqrt {x^{2}+y^{2}}}}+x}}.}$

해당 도메인의 √x² + y + x² ≠ 0에 유의하십시오.

파생상품

atan2 함수는 두 변수의 함수인 만큼 두 개의 부분파생상품이 있다. 이러한 파생상품이 존재하는 지점에서 atan2는 상수를 제외하고 아크탄(y/x)과 같다. 따라서 x > 0 또는 y ≠ 0의 경우,

${\displaystyle {\frac{fraged}&#{\frac}{\flac}}{\c}}{\x)={\frac x}}}}{\fractan \refrac {\i}{x}}}{x}+y^{2}}}={\frac {n2}}}}\\\[5pt]&#{\frac {\fract}{\preason y}}}{\preason name {atan2}(y,\,x)={\practan \refractan \prefrac\{y}}}{x}+y^{2}}.\end{정렬}}}$

따라서 atan2의 경사는 다음과 같다.

${\displaystyle \textla{\textan2}}(y,x)=\left-y \over x^{2}+y^{2}},\x \over x^{2}+y^{2}}}\오른쪽).}$

atan2 함수를 각도 함수 θ(x, y) = atan2(y, x)로 비공식적으로 표현하면 총 차이에 대해 다음과 같은 공식이 산출된다.

${\displaystyle {\begin{aligned}\mathrm {d} \theta &={\frac {\partial }{\partial x}}\operatorname {atan2} (y,\,x)\,\mathrm {d} x+{\frac {\partial }{\partial y}}\operatorname {atan2} (y,\,x)\,\mathrm {d} y\\[5pt]&=-{\frac {y}{x^{2}+y^{2}}}\,\mathrm {d}x+{\frac {x}{x^{2}+y^{2}}}}\,\mathrm {d}y.\end{정렬}}}$

atan2 함수는 음의 x축을 따라 불연속적인 반면, 각도가 연속적으로 정의될 수 없다는 사실을 반영하여 이 파생상품은 원점을 제외하고 지속적으로 정의되며, 원점을 제외한 모든 곳에서 각도의 극소수(그리고 실제로 국소적) 변화가 정의될 수 있다는 사실을 반영한다. 경로를 따라 이 파생상품을 통합하면 경로에 걸친 각도의 총체적 변화가 발생하며, 폐쇄 루프에 걸쳐 통합하면 구불구불한 수가 발생한다.

미분 기하학의 언어에서, 이 파생상품은 하나의 형태로서, 닫힌 형태(그 파생상품은 0이지만 정확하지는 않다, 즉 함수의 파생상품은 아니다), 사실상 구멍이 뚫린 평면의 최초의 데 람 코호몰리를 생성한다. 이것은 그러한 형태의 가장 기본적인 예로서, 미분 기하학에서는 기본이다.

atan2의 부분파생상품은 삼각함수를 포함하지 않기 때문에 삼각함수를 평가하는데 비용이 많이 들 수 있는 많은 애플리케이션(예: 임베디드 시스템)에서 특히 유용하다.

삽화

이 그림은 단위 원에 라벨을 붙인 원점에서 선택한 광선을 따라 atan2 값을 나타낸다. 값은 라디안 단위로 원 안에 표시된다. 이 도표는 각도가 광선을 따라 0에서 우측으로 시계 반대 방향으로 증가하는 표준 수학 규약을 사용한다. 인수의 순서가 뒤바뀌었다는 점에 유의하십시오. atan2(y, x) 함수는 점(x, y)에 해당하는 각도를 계산한다.

This figure shows the values of ${\displaystyle \arctan(\tan(\theta ))}$ along with ${\displaystyle \operatorname {atan2} (\sin(\theta ),\cos(\theta ))}$ for ${\displaystyle 0\leq \theta \leq 2\pi }$. Both functions are odd and periodic with periods ${\displaystyle \pi }$${\displaystyle \pi }$ and ${\displaystyle 2\pi }$, respectively, and thus can easily be supplemented to any region of real values of ${\displaystyle \theta }$. One can clearly see the branch cuts of the ${\displaystyle \operatorname {atan2} }$-function at ${\displaystyle \theta =\pi }$, and of the ${\displaystyle \mathrm{arc}}$$($tann){\${\displaystyle \frac{\mathrm{displaystyle}}{}}$ $\$${\displaystyle \frac{\mathrm{}}{}}$ } - ${\displaystyle function}$ ∈{{\tfrac {\pi }{2}},\\tfrac {3\pi }{2}}:}에서 기능$.$^[4]

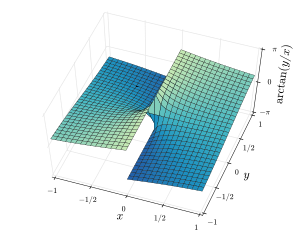
아래의 두 수치는arctan atan2(y는 x)(.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac .num,.mw-parser-output.sfrac .den{의 3D의견을 보여 준다.디스플레이:블록, line-height:1em, 비행기의 지역에 대한 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}y/x cm이다. atan2(y, x)의 경우, 원점에서 방출되는 X/Y 면의 광선은 상수 값을 가지지만, 원점을 통과하는 X/Y 면의 아크탄(y/x) 선의 경우 상수 값을 가진다. x > 0의 경우, 두 도표는 동일한 값을 제공한다.

각도 합계 및 차이 식별

다음 ${\displaystyle \mathrm{ID}}$에 따라$atan2$ {\$displaystyle$ \$operatorname$ {atan2}$}$의 합계를 단일 작업으로 축소할 수 있음$$

${\displaystyle \themp name {atan2}(y_{1},x_{1})\pm \mp {atan2}(y_{2},x_{2}, pm y_{2}x_{1},x_{1}x_{1},mp y_{1},{1},y_{1}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

...the ${\displaystyle \mathrm{atan2}}$ ${\displaystyle }$(${\displaystyle {y\mathrm{}}_{}}$ 1,${\displaystyle {}_{}{x\mathrm{}}_{}}$ ${\displaystyle {1\mathrm{}}_{}{}_{}}$)${\displaystyle }$± ${\displaystyle \mathrm{atan2}}$ ${\displaystyle }$ ${\displaystyle ({}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$,${\displaystyle {}_{}{}_{}}$ 2${\displaystyle {}_{}}$) ${\displaystyle \in }$(${\displaystyle }$- ${\displaystyle \pi }$, ] ${\displaystyle ]}$ ${\displaystyle \operatorname {atan2}$ $(y_{1},x_{1})\pm \epm \atan2}$ $(y_{2},x_{2$

증명에는 두 ${\displaystyle \mathrm{가지}}$ 경우를 고려하는 것이 포함된다. ${\displaystyle {하나}_{}}$는 y 2${\displaystyle {}_{}}$≠ 0$${\$displaystyle y_{$2}\$neq$$$0} x 2 > {\$displaystyle x_$${$2}=$0$$}$이고 ${\displaystyle \mathrm{다른}}$ 하나는 y ${\displaystyle {2\mathrm{}}_{}}$= 0 ${\displaystyle y_{$$2$}=0} 및 < 0 ${\displaystyle x_{0$

${\displaystyle \mathrm{우리}}$는 y ${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ 0 ${\displaystyle y_{2}\neq$ 0$} 또는$ > ${\displaystyle x_{2$}>$0}$의 경우에만 고려한다 시작하기 위해 다음과 같은 관찰을 한다.

1. ${\displaystyle }$-${\displaystyle \mathrm{atan2}}$ ${\displaystyle }$(${\displaystyle y}$, x${\displaystyle }$)${\displaystyle }$= ${\displaystyle \mathrm{atan2}}$ ${\displaystyle }$(${\displaystyle }$- y${\displaystyle }$, ${\displaystyle x}$) ${\displaystyle -\displayname$ {atan2} ($y$$,x)=\displayname {atan2}(-y,x$)}이$($가$$) $0{\displaystyle }$ $displaysty$ y\$neq$ 0$}$ 또는$$ >0 {\$displaystystystystystystystystystystyty,$.
2. ${\displaystyle \operatorname {Arg}(x+iy)=$$\operatorname {atan2}(y,x$ 여기서 ${\displaystyle \mathrm{Arg}}$ ${\displaystyle \operatorname {Arg}은($는) 복잡한 인수 함수다.
3. ${\displaystyle }$$\theta {\displaystyle }$${\displaystyle }$= ${\displaystyle \mathrm{Arg}}$ ${\displaystyle }$ ${\displaystyle {}^{}}$ ${\displaystyle i^{}}$ ${\$ e$^{i$${\displaystyle \backslash \mathrm{tea}}$$}}}$ ${\displaystyle \theta \in(-\pi ,\pi ])$은 오일러 공식의 결과물이다$.$
4. ${\displaystyle \operatorname {Arg} (e^{i\operatorname {Arg} \zeta _{1}}e^{i\operatorname {Arg} \zeta _{2}})=\operatorname {Arg} (\zeta _{1}\zeta _{2})}$.

To see (4), we have the identity ${\displaystyle e^{i\operatorname {Arg} \zeta }={\bar {\zeta }}}$ where ${\displaystyle {\bar {\zeta }}=\zeta /\left \zeta \right }$, hence ${\displ$$aystyle \operatorname {Arg} (e^{i\operatorname {Arg} \zeta _{1}}e^{i\operatorname {Arg} \zeta _{2}})=\operatorname {Arg} ({\bar {\zeta _{1}}}{\bar {\zeta _{2}}})}$. Furthermore, since ${\displaystyle \operatorname {Arg} \zeta =\operatorname {Arg} a\zeta }$ for any positive real value ${\displaystyle a}$, then if we let ${\displaystyle \zeta =\zeta _{1}\zeta _{2}}$ and ${\displaystyle a={\frac {1}{\left \zeta _{1}\right \left \zeta _{2}\right }}}$ then we have ${\displaystyle \operatorname {Arg} ({\bar {\zeta _{1$$}}}{{\bar {\zeta _{2}}=\operatorname {Arg}(\zeta _{1}\zeta$ _${2})$.

이러한 관측치로부터 다음과 같은 동등성이 있다.

${\displaystyle{\begin{정렬}\operatorname{atan2},{}=\operatorname{atan2}(y_{1},x_{1})+\operatorname{atan2}(\pm y_{2},x_{2})&,{\text{에 의해(1)}}\\&,{}=\operatorname{아르지닌}(x_{1}+iy_{1})+\operatorname{아르지닌}(x_{2}\pm{2iy_})&,{\text{에 의해(2)}}\\&,{}=\operatorname{아르지닌}e^{나는(\oper\operatorname{atan2}(y_{2},x_{2})&(y_{1},x_{1})\pm.atorname{아르지닌}(x_{1}}+iy_{1}+\operatorname {Arg}(x_{2}\pm iy_{2})}&{\text{by (3)}}\\&{}=\operatorname {Arg} (e^{i\operatorname {Arg} (x_{1}+iy_{1})}e^{i\operatorname {Arg} (x_{2}\pm iy_{2})})\\&{}=\operatorname {Arg} ((x_{1}+iy_{1})(x_{2}\pm iy_{2}))&{\text{by (4)}\&amp;{}=\operatorname {Arg}(x_{1}x_{2}\mp y_{1}y_{2}+i(y_{1}x_{2}}\pm y_{2}x_{1})\\&{}=\cHB 이름 {atan2}(y_{1}x_{2}\pm y_{2}x_{1}x_{1}x_{1}x_{2}\mp y_{1}y_{2}}&#text{by(2)}}}}\context{nd{aigned}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

Corollary: if ${\displaystyle (y_{1},x_{1})}$ and ${\displaystyle (y_{2},x_{2})}$ are 2-dimensional vectors, the difference formula is frequently used in practice to compute the angle between those vectors with the help of ${\displaystyle \operatorname {atan2} }$, since the resulting 계산은 범위$({\displaystyle }$- ${\displaystyle \pi }$ ,${\displaystyle \pi }$ ${\displaystyle ]}$ ${\displaystyle(-\pi ,\pi ])$에서 양성으로 작용하므로$$ 많은 실제 상황에서 범위 점검 없이 사용할 수 있다.

동-반시계, 북-시계 및 남-시계 규칙 등

${\displaystyle \mathrm{t}}$ n ${\displaystyle 2}$ ${\$ 함수는$$ 원래 동-반시계방향으로 구분할 수 있는 순수 수학에서 규약을 위해 설계되었다. 그러나 실제 적용에서는 북-시계 및 남-시계의 규약이 표준이 되는 경우가 많다. 예를 들어, 대기 과학에서 풍향은 바람 벡터의 동측 및 북측 구성요소를 논거로 하는 ${\displaystyle \mathrm{t}}$ ${\displaystyle \mathrm{n}}$ ${\displaystyle 2}$ ${\$ 함수를$$ 사용하여 계산할 수 있으며,^[5] 태양 방위각은 태양 벡터의 동측 및 북측 구성요소를 논거로 하여 유사하게 계산할 수 있다. 풍향은 일반적으로 북-시계방향으로 정의되며, 태양 방위각은 북-시계방향과 남-시계방향의 규약을 모두 광범위하게 사용한다.^[6] 이러한 서로 다른 규약은 다음과 같이 입장을 교환하고 x와 y의 논거의 기호를 변경함으로써 실현될 수 있다.

• ${\displaystyle \mathrm{a}}$ t ${\displaystyle \mathrm{a}}$ ${\displaystyle \mathrm{n}}$ ${\displaystyle 2}$( y${\displaystyle }$, ${\displaystyle x}$)${\displaystyle }$, $displaystyle \mathrm {atan2}(y,x),\;\;\;\;\;}($동-시계 반대 방향 협약)
• ${\displaystyle \mathrm{a}}$ t ${\displaystyle \mathrm{a}}$ n ${\displaystyle 2}$( x${\displaystyle }$, ${\displaystyle y}$)${\displaystyle }$, $displaystyle \mathrm {atan2}(x,y),\;\;\;\;\;}($북-시계 협약)
• ${\displaystyle \mathrm{a}}$ t ${\displaystyle \mathrm{a}}$ ${\displaystyle \mathrm{n}}$ ${\displaystyle 2}$(${\displaystyle }$- x${\displaystyle }$,${\displaystyle }$- ${\displaystyle y}$) ${\displaystyle \mathrmatrix {atan2}(-x,-y)}$. (남시계 협약)

As an example, let ${\displaystyle x_{0}={\frac {\sqrt {3}}{2}}}$ and ${\displaystyle y_{0}={\frac {1}{2}}}$, then the east-counterclockwise format gives ${\displaystyle \mathrm {atan2} (y_{0},x_{0})\cdot {\frac {180}{\pi }}=30^{\circ }}$$$, the north-clockwise format gives ${\displaystyle \mathrm {atan2} (x_{0},y_{0})\cdot {\frac {180}{\pi }}=60^{\circ }}$, and the south-clockwise format gives ${\displaystyle \mathrm {atan2} (-x_{0},-y_{0})\cdot {\frac$${180}{\pi }=-120^{\pi$ $\}\}\}.$

분명히 x ${\displaystyle \mathrm{및}}$/또는 y-론의 기호를 변경하고 위치를 스와핑하면 ${\displaystyle \mathrm{t}}$ ${\displaystyle \mathrm{2}}$ ${\$ 함수의$$ 가능한 변형이 8개 발생할 수 있으며, 흥미롭게도 각도의 8개 정의 즉, 4개의 기본 방향에서 시작하여 시계 방향 또는 시계 반대 방향과 일치한다.s, 북쪽, 동쪽, 남쪽, 서쪽.

공통 컴퓨터 언어의 기능 실현

기능의 실현은 컴퓨터 언어마다 다르다.

• C 함수 atan2, 그리고 대부분의 다른 컴퓨터 구현은 데카르트 좌표를 극좌표로 변환하는 노력을 줄이도록 설계되었으며, 따라서 항상 정의한다. atan2(0, 0). 서명된 0이 없는 구현에서 또는 양의 0 인수가 주어지면 일반적으로 0으로 정의된다. 오류를 발생시키거나 NaN(숫자가 아님)을 반환하지 않고 항상 [-π, π] 범위의 값을 반환한다.
• 선택적 인수가 존재하는 Common Lisp에서는 atan 함수를 사용하면 X 좌표를 선택적으로 제공할 수 있다. (atan y x).^[7]
• 줄리아에서 상황은 커먼 리스프(Common Lisp)와 비슷하다. atan2, 그 언어는 1와 2의 형태를 가지고 있다. atan단,^[8] 컴파일 시 공격적인 최적화를 허용하는 방법에는 세 가지가 넘는 방법이 있다("Julia에게 Matlab/Python/R/ 코드를 컴파일하지 않으시겠습니까?" 섹션 참조).
• Mathematica에서 그 형태는 ArcTan[x, y] 하나의 매개변수 양식이 정규 아크탄젠트를 제공하는 경우에 사용된다(위의 논의에서 사용된 규약과 비교하여 논쟁의 순서가 뒤바뀌는 점에 유의한다). 매스매티카는 분류한다. ArcTan[0, 0] 애매한 표현으로
• Microsoft Excel,^[10][14]OpenOffice.org Calc, LibreOffice Calc,^[11] Google 스프레드시트,^[12] iWork Numbers ^[13]및 ANSI SQL:2008 표준에서 atan2 함수는 두 주장을 뒤집었다.
• Intel Architecture Assembler 코드에서 atan2 라고 알려져 있다. FPATAN (부분 아크탄젠트 지점) 지침.^[15] 그것은 불의를 다룰 수 있고 결과는 닫힌 간격[-closed, in]에 있다. atan2(∞, x) = 유한 x의 경우 +102/2. 특히, FPATAN 두 인수 모두 0일 때 정의됨:

  atan2(+0, +0) = +0;

  atan2(+0, −0) = +π;

  atan2(−0, +0) = −0;

  atan2(−0, −0) = −π.

이 정의는 서명된 0의 개념과 관련이 있다.

• 대부분의 TI 그래프 작성 계산기(TI-85와 TI-86 제외)에서는 등가함수를 R►Pθ이라 하고 그 주장을 뒤집는다.
• TI-85에서는 arg 함수를 부른다. angle(x,y) 그리고 비록 그것이 두 개의 주장을 취하는 것처럼 보이지만, 실제로는 x + y = (x, y)라는 한 쌍의 숫자로 표시되는 하나의 복잡한 주장만을 가지고 있다.
• 책이나 기사와 같이 소스 코드 이외의 수학적 저술에서는 아크탄과^[16]−1[17] 탄이라는 공식이 활용되었다. 이것들은 일반 아크탄과 황갈의⁻¹ 자본화된 변형이다. 이 용법은 아탄(y, x) = 아그(x + i)와 같은 복잡한 인수 표기법과 일치한다.
• HP 계산기에서 좌표를 복잡한 숫자로 처리한 다음 ARG. 또는 << C->R ARG >> 'ATAN2' STO.
• 과학적 계산기에서 함수는 직사각형 좌표에서 극좌표로 (x, y) 변환될 때 주어진 각도로 계산될 수 있다.
• 기호수학을 지원하는 시스템은 일반적으로 atan2(0, 0)에 대해 정의되지 않은 값을 반환하거나 비정상적인 상태가 발생했음을 신호한다.
• 서명된 0, infinities 또는 Not a Number(예: IEEE 부동 소수점)를 구현하는 시스템의 경우, -properties 및 -0을 포함하도록 생산되는 값의 범위를 확장할 수 있는 합리적인 확장을 구현하는 것이 일반적이다. 또한 NaN을 반환하거나 NaN 논거가 주어졌을 때 예외를 제기할 수 있다.
• 서명된 0(예: IEEE 부동소수점), atan2(-0, x), x < 0은 atan2(y, x)의 구현이 -0 입력을 제대로 처리하지 못하는 경우 -message를 반환할 위험을 내포한다.
• 넷리브에서 사용할 수 있는 무료 수학 라이브러리 FDLIBM(자유분배 가능 LIBM)에는 구현 방법을 보여주는 소스 코드가 있다. atan2 다양한 IEEE 예외 값 취급 포함.
• 하드웨어 승수가 없는 시스템의 경우 atan2 기능은 CODRIC 방법에 의해 수치적으로 신뢰할 수 있는 방식으로 구현될 수 있다. 따라서 atan(y)의 구현은 atan2(y, 1)를 계산하는 것을 선택할 것이다.

참고 항목

• 하이픈을 치다

참조

외부 링크

• ATAN2 온라인 계산기
• Java 1.6 SE JavaDoc
• Everything2 atan2 at everything2
• PIC18F용 PicBasic Pro 솔루션 atan2

atan2에 대한 기타 구현/코드

• 두 점 사이의 베어링
• 아크탄 및 극좌표
• '아르코스'가 뭐야?

메모들