복잡한 분석
Complex analysis| 수학적 해석 → 복소해석 |
| 복잡한 분석 |
|---|
 |
| 복소수 |
| 복잡한 기능 |
| 기본 이론 |
| 기하함수론 |
| 사람 |
전통적으로 복소수 함수 이론으로 알려진 복소수 분석은 복소수의 함수를 조사하는 수학 분석의 한 분야이다.그것은 대수 기하학, 수 이론, 해석 조합론, 응용 수학뿐만 아니라 유체역학, 열역학, 그리고 특히 양자역학을 포함한 물리학 분야에서도 도움이 됩니다.더 나아가 복잡한 분석의 사용은 원자력, 항공우주, 기계 및 전기 [citation needed]공학 같은 공학 분야에서도 적용된다.
복소수의 미분 가능 함수는 테일러 급수와 동일하기 때문에(즉, 분석적), 복소수 분석은 복소수의 해석 함수(즉, 정형 함수)에 특히 관심을 갖는다.
역사
복소해석학은 수학의 고전적인 분야 중 하나이며, 18세기에 뿌리를 두고 있습니다.복소수와 관련된 중요한 수학자들은 오일러, 가우스, 리만, 코치, 바이어스트라스, 그리고 20세기의 더 많은 수학자들을 포함합니다.복잡한 해석, 특히 등각 매핑 이론은 많은 물리적 응용 분야를 가지고 있으며, 또한 해석적 수 이론 전반에 걸쳐 사용된다.현대에 와서는 복잡한 역학에서 비롯된 새로운 부스트와 신성함수 반복으로 생성된 프랙탈의 그림으로 인해 매우 인기를 끌고 있다.복잡한 분석의 또 다른 중요한 적용은 양자장 이론에서 등각 불변성을 조사하는 끈 이론이다.
복잡한 기능
복소함수는 복소수에서 복소수까지의 함수입니다.즉, 복소수의 서브셋을 도메인으로, 복소수를 코도메인으로 하는 함수입니다.복잡한 함수는 일반적으로 복잡한 평면의 비어 있지 않은 열린 서브셋을 포함하는 도메인을 갖는 것으로 가정됩니다.
복잡한 기능의 경우 도메인에서 zz) 과 범위 내의 f f를 실제 부분과 가상의 부분으로 구분할 수 있습니다.
서 x ( ,) , ( , ) , v ( x , y x , , ) }는 모두 실수치입니다.
즉, f : {\ f \는 다음과 같이 분해될 수 있다.
- : {\ u : {\{R \
즉, 두 개의 실제 변수( x y의 두 개의 실제 값 함수( u v로 나눕니다.
마찬가지로 임의의 집합 X 상의 복소수 함수 f는 (Re f, Im f) 또는 X에서 2로의 값 함수로 간주할 수 있습니다
복소수 함수의 일부 특성(예: 연속성)은 두 실제 변수의 벡터 값 함수의 해당 특성에 지나지 않습니다.미분성과 같은 복잡한 분석의 다른 개념은 실제 기능에 대한 유사한 개념의 직접적인 일반화이지만, 매우 다른 속성을 가질 수 있다.특히, 모든 미분 가능한 복합 함수는 분석적이며(다음 절 참조), 점 근처에서 동일한 두 개의 미분 가능한 함수는 해당 영역의 교차점에서 동일하다(도메인이 연결된 경우).후자의 속성은 유한한 수의 곡선 호가 제거된 전체 복소 평면인 복소 해석 함수를 얻기 위해 모든 실제 해석 함수를 독특한 방식으로 확장할 수 있는 해석 연속 원리의 기초이다.복소수 지수 함수, 복소수 로그 함수, 삼각 함수 등 많은 기본 및 특수 복소수 함수가 이러한 방식으로 정의됩니다.
정칙함수
복소평면의 열린 부분집합(\의 모든 점에서 미분 가능한 복소함수는(\에서 정칙형이라고 하며, 복소해석에서는 z })에서f(\ f의 도함수를 정의한다.
표면적으로 이 정의는 형식적으로 실함수의 도함수와 유사하다.그러나 복잡한 도함수와 미분 가능한 함수는 실제 도함수에 비해 상당히 다른 방식으로 동작한다.특히 이 한계가 존재하기 위해서는 복소 에서 z 00})에 접근하는 방식에 관계없이 차분 비율의 값이 동일한 복소수에 근접해야 한다.결과적으로, 복잡한 미분성은 실제 미분성보다 훨씬 더 강력한 의미를 갖는다.예를 들어, n차 도함수의 존재는 실함수에 대한 (n + 1)차 도함수의 존재를 의미할 필요는 없다.또한 모든 정형 함수는 더 강력한 해석 조건을 충족하며, 이는 함수가 영역의 모든 점에서 수렴력 계열에 의해 국소적으로 주어진다는 것을 의미합니다.본질적으로, 는 의 모든 점 근처에서 다항식으로의 함수를 로근사할 수 있다는 것을 한다. 는 미분 가능한 실함수와 극명한 대조를 이룬다 즉, 항문 어디에도 없는 무한히 미분 가능한 실함수가 존재한다.non-analysismooth function(비분석적 평활함수) 참조. 어느 곳에서도 실제 분석이 되지 않는 평활함수.
함수 C \ \ 로서 복소수 인수로 적절히 확장되는 대부분의 기본 함수는 전체 복소 평면에 걸쳐 완전함수인 반면, 합리적인 p./ { p} (여기서 p와 q는 다항식)는 q가 0인 점을 제외하는 도메인에서 홀모픽입니다고립된 점 집합을 제외한 모든 곳에서 정형 함수인 이러한 함수를 정형 함수라고 합니다.한편, (z ) \ z \\ ) z z \ {\ z z {\ z {\ z {\ z {\ z {\ z z {\ z {\ z {\ z {\ { bar { z}{ z { {\ on on on on on on on on on on on on on on on on on on on on on on on on on on
홀모픽 함수의 중요한 특성은 코시-리만 조건이라고 알려진 실재 성분과 허수 성분의 부분 도함수 사이의 관계이다.: {\ f \f( + y ) (x ,) + v ( ,) { f ( z ) ( x + ) = ( ) + y ) ( y ) 、 x ) ) 、 x , , x ) 。 모든 0 \
함수 u와 v의 실수 부분과 허수 부분에서는 x yx} =y} - x - y u different u y u u in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in그러나, 코시-리만 조건은 추가적인 연속성 조건 없이 정칙함수를 특징짓지 않는다. (루만-멘초프 정리 참조)
홀모픽 함수는 몇 가지 주목할 만한 특징을 보인다.예를 들어, Picard의 정리에서는 전체 함수의 범위는 C{ ∖ { z \ \의 형식만 사용할 수 있습니다즉, 두 개의 서로 다른 z z)와 w w가 전체 f(\f의 범위에 있지 않은 경우 f f는 상수 함수입니다.게다가 접속된 오픈 세트상의 홀모픽 함수는, 비어 있지 않은 오픈 서브셋에의 제한에 의해서 결정된다.
주요 결과
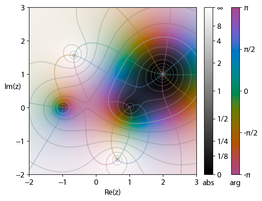
색상은 인수를 나타내고 밝기는 크기를 나타냅니다.
복합 분석의 중심 도구 중 하나는 선 적분입니다.닫힌 경로에 의해 경계된 영역 내의 모든 곳에서 정칙형인 함수의 닫힌 경로 주변의 선 적분은 코시 적분 정리에 의해 명시된 바와 같이 항상 0입니다.디스크 내의 이러한 완전함수 값은 디스크의 경계에 있는 경로 적분으로 계산할 수 있습니다(코치의 적분 공식에 표시됨).복합 평면의 경로 적분은 종종 복잡한 실제 적분을 결정하기 위해 사용되며, 여기에는 다른 것들 간의 잔류물 이론이 적용된다(윤곽선 통합 방법 참조).함수의 "극"(또는 고립된 특이점)은 함수의 값이 무제한이 되거나 "확대"되는 지점입니다.만약 어떤 함수에 그러한 극이 있다면, 그 함수의 잔차를 계산할 수 있고, 이것은 함수와 관련된 경로 적분을 계산하는데 사용될 수 있다. 이것이 강력한 잔차 정리이다.본질적인 특이점에 가까운 홀모픽 함수의 주목할 만한 행동은 피카르의 정리에 의해 설명된다.극만 있고 본질적인 특이점이 없는 함수를 meromaphy라고 합니다.Laurent 급수는 Taylor 급수와 같은 복소수 값이지만, 다항식과 같이 더 잘 이해된 함수의 무한한 합계를 통해 특이점 근처 함수의 행동을 연구하는 데 사용될 수 있다.
전체 복소평면에서 정칙인 유계함수는 일정해야 한다. 이것이 리우빌의 정리이다.그것은 복소수 필드가 대수적으로 닫혀 있다는 대수학의 기본 정리에 대한 자연스럽고 짧은 증거를 제공하기 위해 사용될 수 있다.
함수가 연결된 도메인 전체에 걸쳐 완전 형상인 경우, 그 값은 더 작은 서브 도메인 상의 값에 의해 완전히 결정됩니다.큰 도메인의 함수는 작은 도메인의 값에서 분석적으로 계속된다고 한다.이를 통해 리만 제타 함수와 같은 함수의 정의를 확장할 수 있으며, 처음에는 제한된 영역에서만 수렴하는 무한합계의 관점에서 정의되어 거의 전체 복소 평면으로 확장된다.자연대수의 경우처럼 복소수 평면에서 단순하지 않은 연결 영역으로 해석적으로 홀모픽 함수를 계속하는 것은 불가능하지만, 리만 표면으로 알려진 밀접하게 관련된 표면에서 홀모픽 함수로 확장하는 것은 가능하다.
이 모든 것은 하나의 변수에 대한 복잡한 분석을 의미합니다.또한 하나의 복잡한 차원(예: 적합성)에 있는 홀모픽 함수의 기하학적 특성 대부분이 이월되지 않는 반면, 멱급수 팽창과 같은 분석 특성이 계승되는 하나 이상의 복잡한 차원에서의 매우 풍부한 복소 해석 이론이 있다.1차원 이론에서 가장 중요한 결과일 수 있는 복소 평면에서의 특정 도메인의 등각 관계에 대한 리만 매핑 정리는 고차원에서는 극적으로 실패한다.
양자역학에서 파동함수로서 어떤 복잡한 공간의 주요한 응용이 있다.
「 」를 참조해 주세요.
레퍼런스
- Ablowitz, M. J. & A. S. Fokas, 복합 변수: 개요와 응용 프로그램(Cambridge, 2003).
- Ahlfors, L., 복합 분석(McGrow-Hill, 1953).
- Cartan, H., Théorie élémentaire des fonctions analytiques d'une you plusieurs 변수 복합체.(헤르만, 1961).영어 번역, 하나 또는 여러 복합 변수의 분석 함수의 기초 이론(Addison-Wesley, 1963).
- 카라테오도리, C, 펑크티온텐테오리(Birkhauser, 1950).영어 번역, 복합 변수의 함수 이론(Chelsea, 1954).[2권]
- 반송파, G.F., M. Krook 및 C. E. Pearson, 복합 변수의 함수: 이론과 기술. (McGrow-Hill, 1966).
- Conway, J. B., 단일 복소 변수의 함수. (스프링어, 1973).
- Fisher, S., Complex Variables. (Wadsworth & Brooks/Cole, 1990).
- Forsyth, A., 복소 변수의 함수 이론(Cambridge, 1893)
- Freitag, E. & R. Busam, Funktionentheory.(Springer, 1995).영어 번역, 복합 분석.(Springer, 2005).
- Goursat, E., Cours d'analyze mathématique, tome 2. (Gauthier-Villars, 1905).영어 번역, 수학 해석의 과정, 제2권, 제1부: 복소 변수의 함수. (Ginn, 1916).
- Henrici, P., Applied and Computational Complex Analysis (Wiley).[3권 1974, 1977, 1986]
- Kreysigig, E., Advanced Engineering Mathematics (Wiley, 1962).
- Lavrentyev, M. & B. Shabat, мт lav lav lav lav lav lav lav lav lav lav lav lav lav lav lav lav lav lav lav lav lav lav ( Methods of the Functions of Functions of a Complex Variable ) 。(1951년, 러시아어).
- Markushevich, A. I., 복소변수 함수론, (Prentice-Hall, 1965).[3권]
- Marsden & Hoffman, Basic Complex Analysis. (Freeman, 1973년).
- Needham, T., Visual Complex Analysis.(Oxford, 1997).http://usf.usfca.edu/vca/
- Remmert, R., 복소함수 이론. (스프링어, 1990).
- Rudin, W., Real 및 Complex Analysis.(McGrow-Hill, 1966).
- Shaw, W. T., Mathematica를 사용한 복소해석(Cambridge, 2006).
- Stein, E. & R. Shakarchi, 복합 분석. (Princeton, 2003).
- Sveshnikov, A. G. & A. N. Tikhonov, Теория функций комплексной переменной. (Nauka, 1967).영어 번역, 복합 변수의 함수 이론(MIR, 1978).
- Titchmarsh, E.C., 함수론 (Oxford, 1932).
- Wegert, E., Visual Complex Functions.(Birkhaeuser, 2012).
- Whittaker, E. T. & G. N. Watson, A Course of Modern Analysis.(Cambridge, 1902).제3판 (제3판


 범위 내의
범위 내의  실제 부분과
실제 부분과 

 다음과 같이 분해될 수 있다.
다음과 같이 분해될 수 있다.





 모든 점에서
모든 점에서 
 도함수를 정의한다.
도함수를 정의한다.













 전체
전체 

