회전행렬

선형 대수학에서 회전 행렬은 유클리드 공간에서 회전을 수행하는 데 사용되는 변환 행렬입니다. 예를 들어, 아래의 관례를 이용하면 행렬은

${\displaystyle R={\begin{bmatrix}\cos \theta &-\sin \theta &\cos \end{bmatrix}}$

2차원 직각좌표계의 원점에 대한 각도 θ를 통해 xy 평면의 점을 반시계 방향으로 회전시킵니다. 표준 좌표 v = (x, y)인 평면 점에서 회전을 수행하려면 열 벡터로 작성하고 행렬 R을 곱해야 합니다.

${\displaystyle R\mathbf {v} = {\begin{bmatrix}\cos \theta &-\sin \theta \\sin \theta &\cos \end{bmatrix}{\begin{bmatrix}x\y\end{bmatrix}}={\begin{bmatrix}x\cos \theta +y\cos \end{bmatrix}}}$

x와 y가 벡터의 끝점 좌표이고, 여기서 x는 코사인이고 y는 사인이면 위의 방정식은 삼각합각 공식이 됩니다. 실제로 회전 행렬은 행렬 형태의 삼각 합산 각도 공식으로 볼 수 있습니다. 이것을 이해하는 한 가지 방법은 x축으로부터 30° 떨어진 각도에 벡터가 있고, 그 각도를 45° 더 회전하고 싶다고 말하는 것입니다. 75°의 벡터 끝점 좌표를 계산하기만 하면 됩니다.

이 글의 예는 사전 곱셈(왼쪽의 R)에 의해 오른손 좌표계에서 반시계 방향으로(x에서 반시계 방향으로 y) 벡터의 능동적 회전에 적용됩니다. 이 중 하나라도 변경되면(벡터 대신 회전축, 수동 변환 등) 예제 행렬의 역행렬을 사용해야 하며, 이는 전치행렬과 일치합니다.

행렬 곱셈은 영벡터(원점의 좌표)에 영향을 미치지 않기 때문에 회전 행렬은 원점에 대한 회전을 설명합니다. 회전 행렬은 이러한 회전에 대한 대수적 설명을 제공하며 기하학, 물리학 및 컴퓨터 그래픽의 계산에 광범위하게 사용됩니다. 일부 문헌에서 회전이라는 용어는 부적절한 회전을 포함하는 것으로 일반화되며, (+1 대신) 행렬식을 갖는 직교 행렬로 특징지어집니다. 이들은 적절한 회전과 반사(역방향)를 결합합니다. 반사가 고려되지 않는 다른 경우에는 라벨 고유의 라벨이 삭제될 수 있습니다. 이 글에서는 후자의 관례를 따릅니다.

회전 행렬은 실제 항목이 있는 정사각형 행렬입니다. 좀 더 구체적으로 말하면, 행렬식 1을 갖는 직교 행렬로 특징지어질 수 있습니다. 즉, R = R 및 detR = 1인 경우에만 정방행렬 R이 회전 행렬입니다. 행렬식 +1을 갖는 크기 n의 모든 직교 행렬의 집합은 특수 직교 그룹 SO(n)로 알려진 그룹의 표현이며, 그 중 하나의 예는 회전 그룹 SO(3)입니다. 행렬식 +1 또는 -1을 갖는 크기 n의 모든 직교 행렬의 집합은 (일반적인) 직교 그룹 O(n)의 표현입니다.

2차원으로

2차원에서 표준 회전 행렬은 다음과 같은 형태를 갖습니다.

${\displaystyle R(\theta)={\begin{bmatrix}\cos \theta &-\sin \theta &\cos \\end{bmatrix}}}$

이것은 다음 행렬 곱셈을 통해 열 벡터를 회전시킵니다.

${\displaystyle {begin{bmatrix}x'\\y'\\end{bmatrix}={\begin{bmatrix}\cos \theta &-\sin \theta &-\sin \theta &\cos \\end{bmatrix}}{\begin{bmatrix}x\y\\end{bmatrix}}}$

따라서, 회전 후의 한 점(x, y)의 새로운 좌표(x', y')는

${\displaystyle {\begin{aligned}x'&=x\cos \theta \,\y'&=x\sin \theta +y\cos \theta \,\end{aligned}}}$

예

예를 들어 벡터가

${\displaystyle \mathbf {\hat {x} = {\begin {bmatrix}1\\0\\end{bmatrix}}}$

각도 θ에 의해 회전되며, 새로운 좌표는

${\displaystyle {\begin {bmatrix}\cos \theta \\sin \\\end {bmatrix}},}$

그리고 벡터가

${\displaystyle \mathbf {\hat {y} = {\begin {bmatrix} 0\\1\\end{bmatrix}}}$

각도 θ에 의해 회전되며, 새로운 좌표는

${\displaystyle {\begin{bmatrix}-\sin \theta \\cos \theta \\end{bmatrix}}}$

방향

벡터 회전 방향은 θ이 양이면 반시계 방향(예: 90°)이고, θ이 음이면 시계 방향(예: -90°)입니다. $($θ) {\$displaystyle$R$(\backslash$theta)}의 경우. 따라서 시계 방향 회전 행렬은 다음과 같습니다.

${\displaystyle R(-\theta)={\begin{bmatrix}\cos \theta &\sin \theta &\cos \\end{bmatrix}}}$

2차원 케이스는 회전 행렬 그룹이 교환 가능한 유일한 사소하지 않은(즉, 1차원이 아닌) 케이스이므로 어떤 순서로 여러 회전을 수행하는지는 중요하지 않습니다. 대안적인 관례는 회전축을 사용하며, 위 행렬들은 또한 각도 θ을 통해 시계 방향으로 축들의 회전을 나타냅니다.

좌표계의 비표준 방향

x축을 오른쪽으로 하고 y축을 위쪽으로 하는 표준 오른손 직각좌표계를 사용하는 경우 회전 R(θ)은 반시계 방향입니다. x가 오른쪽을 향하지만 y가 아래를 향하도록 하는 왼손 직각좌표계를 사용하는 경우 R(θ)은 시계 방향입니다. 이러한 비표준 방향은 수학에서 거의 사용되지 않지만 2D 컴퓨터 그래픽에서 흔히 사용되며, 왼쪽 상단 모서리에 원점이 있고 화면이나 페이지 아래에 y축이 있는 경우가 많습니다.^[2]

회전 행렬에 의해 생성되는 회전의 감각을 변경할 수 있는 다른 대안 규칙은 아래를 참조하십시오.

공통 2D 회전

특히 유용한 것은 행렬입니다.

${\displaystyle {\begin{bmatrix}0&-1\\[3pt]1&0\\\end{bmatrix}},\quad {\begin{bmatrix}-1&0\\[3pt]0&-1\\\end{bmatrix}},\quad {\begin{bmatrix}0&1\\[3pt]-1&0\\\end{bmatrix}}}$

90°, 180°, 270° 반시계 방향 회전 시.

복소평면과의 관계

부터

${\displaystyle {\begin{bmatrix}0&-1\\1&0\end{bmatrix}}^{2}\ =\ {\begin{bmatrix}-1&0\\0&-1\end{bmatrix}}\ =-I,}$

형체의 행렬

${\displaystyle {\begin{bmatrix}x&y\y&x\end{bmatrix}}}$

$복소수{\displaystyle \mathbb{}}$ C ${\$의 필드와 동형인 고리를 형성합니다$.$ 이 동형 아래에서 회전 행렬은 단위 복소수인 모듈러스 1의 복소수의 원에 해당합니다.

선형 동형$({\displaystyle a,}$ ${\displaystyle b)}$ ↦${\displaystyle }$a +$ib$, ${\displaystyle$$\mathbb {R} ^{2}}$을(를) $C$ ${\displaystyle$\$mathbb$${C}}$로 식별하면$,$$}$${\displaystyle {\mathrm{}}^{}}$ ${\$ 의 벡터에 대한 위 형태의 행렬의 작용은$$ 복소수 x + iy에 의한 곱셈에 해당하고$$, 회전은 모듈러스 1의 복소수에 의한 곱셈에 해당합니다.

모든 회전 행렬을 작성할 수 있으므로

${\displaystyle {\begin{pmatrix}\cost t&-\sin t&\cost\end{pmatrix}}}$

위의 대응문은 그러한 행렬을 복소수와 연관짓습니다.

${\displaystyle \cost+i\sin t=e^{it}$

(이 마지막 등식은 오일러 공식입니다.)

입체적으로

기본 3D 회전

기본 3D 회전(원소 회전이라고도 함)은 좌표계의 축 중 하나를 중심으로 회전하는 것입니다. 다음 세 개의 기본 회전 행렬은 x축, y축 또는 z축에 대해 3차원으로 각도 θ만큼 벡터를 회전시키며, 이들의 교대 부호를 부호화하는 오른손 규칙을 사용합니다. 오른손 규칙은 ${\displaystyle R}$ ⋅ x$$→ ${\displaystyle R\cdot {\$vec $\{$x}}을(를) 곱할 때만 작동합니다. (같은 행렬은 축의 시계방향 회전도 나타낼 수 있습니다.)

${\displaystyle {\begin{alignat}{1}R_{x}(\theta)&={\begin{bmatrix}1&0\\0&\cos \theta &-\sin \theta \[3pt]0&\sin \theta &\cos \[3pt]\end{bmatrix}}\[6pt]R_{y}(\theta )&={\begin{bmatrix}\cos \theta &0&\sin \theta \\[3pt]0&1&0\\[3pt]-\sin \theta &0&\cos \theta \\\end{bmatrix}}\\[6pt]R_{z}(\theta)&={\begin{bmatrix}\cos \theta &-\sin \theta &0\\[3pt]\sin \theta &\cos \theta &0\\[3pt]0&0&1\\\end{bmatrix}}\end{alignat}}$

열 벡터의 경우 각 기본 벡터 회전은 발생하는 축이 관찰자를 가리키고, 좌표계가 오른손잡이이며, 각도 θ이 양수일 때 시계 반대 방향으로 나타납니다. 예를 들어, 벡터_z (1,0,0)에서 R로_z 작동하여 쉽게 확인할 수 있는 것처럼, R은 x축과 정렬된 벡터를 y축을 향해 회전합니다.

${\displaystyle R_{z}(90^{\circ }){\begin{bmatrix}1\\0\0\\end{bmatrix}={\begin{bmatrix}\cos 90^{\circ }&-\sin 90^{\circ }&0\\\sin 90^{\circ }&\quad \cos 90^{\circ }&0\\0&0&1\\\end{bmatrix}}{\begin{bmatrix}1\\0\\0\\\end{bmatrix}}={\begin{bmatrix}0&-1&0\\1&0&0\\0&0&1\\\end{bmatrix}}{\begin{bmatrix}1\\0\\0\\\end{bmatrix}}={\begin{bmatrix}0\\1\\0\\\end{bmatrix}}}$

이는 앞서 언급한 2차원 회전행렬에 의해 생성되는 회전과 유사합니다. 이러한 행렬에 의해 생성되는 회전의 감각을 분명히 또는 실제로 반전시킬 수 있는 대안적인 규칙은 아래를 참조하십시오.

일반 3D 회전

행렬 곱셈을 사용하여 이 세 가지로부터 다른 3D 회전 행렬을 얻을 수 있습니다. 예를 들어, 제품은

${\displaystyle {\begin{align}R=R_{z}(\alpha)\,R_{y}(\beta)\,R_{x}(\gamma)&={\overset {\text{yaw}}{\begin{bmatrix}\cos \alpha&-\sin \alpha&0\\\cos \alpha&0\\0&0&1\\\end{bmatrix}}}{\overset {\text{pitch}}{\begin{bmatrix}\cos \beta &0&\sin \beta \\0&1&0\-\sin \beta &0&\cos \beta \\\end{bmatrix}}}{\overset {\text{roll}}{\begin{bmatrix}}}{\cos{bmatrix}} \gamma \\\end{bmatrix}}\\\&={\begin{bmatrix}\cos \alpha \cos \cos \beta &\cos \alpha \sin \gamma -\sin \alpha \cos \cos \cos \cos gamma +\sin \alpha \sin \gamma \gamma +\sin \alpha \beta \cos beta &\sin \alpha \sin \gamma +\cos \cos \cos \cos gamma &\sin \alpha \sin \cos gamma -\alpha \sin \gamma -\-\sin \beta &\cos \sin \gamma &\cos \cos \cos \gamma \beta \\end{bmatrix}\end{align}}$

요, 피치 및 롤 각도가 각각 α, β 및 γ인 회전을 나타냅니다. 보다 형식적으로는 Tait-Bryan 각도가 각각 축 z, y, x에 대해 α, β, γ이 되는 고유 회전입니다. 마찬가지로, 제품은

${\displaystyle {\begin{align}\\\R=R_{z}(\gamma)\,R_{y}(\beta)\,R_{x}(\alpha)&={\begin{bmatrix}\cos \gamma&-\sin \gamma&0\\sin \gamma&0\\cos \gamma&0\\0&0&1\\end{bmatrix}\cos \beta&0&\sin \beta&0&\cos \beta&0&0\cos \beta\\end{bmatrix}}\cos \alpha&0&\cos \begin\\end{bmatrix}}\cos \alpha&-\cos \alpha&0&\cos \alpha \sin \cos \cos \gamma -\cos \alpha \sin \gamma &\cos \alpha \sin \cos \cos \gamma +\sin \alpha \sin \gamma \\cos \gamma \beta \gamma &\sin \alpha \beta \sin \beta +\cos \alpha \cos \cos \cos \gamma &\cos \beta \sin \gamma -\sin \alpha \cos \gamma \\-\sin \alpha \cos \beta &\cos \cos \cos beta &\cos \cos beta \\\end{bmatrix}}\end{align}}$

오일러 각도가 α, β, γ, 축 x, y, z인 외부 회전을 나타냅니다.

이러한 행렬은 열 벡터를 미리 곱하기 위해 사용되는 경우에만 원하는 효과를 생성하고, (일반적으로 행렬 곱셈은 교환적이지 않기 때문에) 지정된 순서로 적용되는 경우에만 원하는 효과를 생성합니다(자세한 내용은 모호성 참조). 회전 작업의 순서는 오른쪽에서 왼쪽으로, 열 벡터에 인접한 행렬이 가장 먼저 적용되고 왼쪽으로 적용됩니다.^[3]

회전행렬에서 축각으로 변환

3차원의 모든 회전은 축(이 축을 따라 있는 벡터는 회전에 의해 변하지 않음)과 그 각도 - 해당 축에 대한 회전량(Euler 회전 정리)에 의해 정의됩니다.

회전 행렬로부터 축과 각도를 계산하는 방법은 여러 가지가 있습니다(축-각도 표현 참조). 여기서는 회전 행렬의 고유 벡터와 고유값 계산을 기반으로 한 방법만 설명합니다. 회전 행렬의 흔적을 사용하는 것도 가능합니다.

축 결정

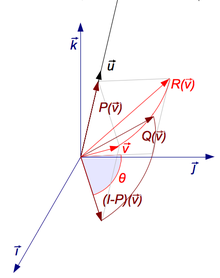
3×3 회전행렬 R이 주어졌을 때, 회전축에 평행한 벡터 u는 다음을 만족해야 합니다.

${\displaystyle R\mathbf {u} =\mathbf {u},}$

당신이 회전축을 중심으로 회전하면 당신이 생겨야 하기 때문입니다. 위의 방정식은 R = I이 아니면 스칼라 인자까지 유일한 u에 대해 풀 수 있습니다.

또한 방정식을 다시 작성할 수도 있습니다.

${\displaystyle R\mathbf {u} = I\mathbf {u} \implies \left(R-I\right)\mathbf {u} = 0,}$

R - I의 널 공간에 있다는 것을 보여줍니다.

다른 관점에서, u는 고유값 λ = 1에 해당하는 R의 고유 벡터입니다. 모든 회전 행렬은 이 고유값을 가져야 하며, 나머지 두 고유값은 서로의 복소수 켤레입니다. 따라서 3차원의 일반 회전 행렬은 곱셈 상수까지 실제 고유 벡터가 하나뿐입니다.

회전축을 결정하는 한 가지 방법은 다음을 보여주는 것입니다.

${\displaystyle {\begin{align}0&=R^{\mathsf {T}0+0\\&=R^{\mathsf {T}\left(R-I\right)\mathbf {u} +\left(R-I\right)\mathbf {u} \\&=\left(R^{\mathsf {T}\right)\mathbf {u} \\&=\left(I-R^{\mathsf {T}+R-I\right)\mathbf {u} \\&=\left(R-R^{\mathsf {t})$

(R^T - R)은 스큐 대칭 행렬이므로 다음과 같이 선택할 수 있습니다.

${\displaystyle [\mathbf {u}}_{\times} =\left(R-R^{\mathsf {T}\right)}$

행렬-벡터 곱은 벡터 자체의 교차 곱이 되어 결과가 0이 되도록 합니다.

${\displaystyle \left(R-R^{\mathsf {T}\right)\mathbf {u} =[\mathbf {u}}_{\times}\mathbf {u} =\mathbf {u} \times \mathbf {u} =0\,}$

따라서 만약

${\displaystyle R={\begin{bmatrix}a&b&c\\d&e&f\\g&h&i\\\end{bmatrix}},}$

그리고나서

${\displaystyle \mathbf {u} = {\begin{bmatrix}h-f\c-g\d-b\\end{bmatrix}}}$

이렇게 계산된 u의 크기는 θ에서 ‖ u ‖ = 2이며, 여기서 θ는 회전 각도입니다.

R이 대칭인 경우에는 적용되지 않습니다. 위에서 R - R이^T 0이면 이후의 모든 단계가 유효하지 않습니다. 이 경우 R을 대각화하여 고유값 1에 해당하는 고유벡터를 찾아야 합니다.

각도결정

회전 각도를 구하려면 회전축이 알려지면 축에 수직인 벡터 v를 선택합니다. 그러면 회전 각도는 v와 Rv 사이의 각도입니다.

그러나 보다 직접적인 방법은 단순히 트레이스, 즉 회전 행렬의 대각선 요소의 합을 계산하는 것입니다. 각도 θ가 선택한 축과 일치하도록 올바른 기호를 선택하려면 주의해야 합니다.

${\displaystyle \operatorname {tr}(R)=1+2\cos \theta,}$

각도의 절대값은 다음과 같습니다.

${\displaystyle \theta =\arccos \left ({\frac {\operatorname {tr}(R)-1}{2}}\right)}$

회전축 $n$ =${\displaystyle }$(${\displaystyle {}_{}}$ ${\displaystyle 1_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle 2_{}}$ ${\displaystyle n_{}}$ 3${\displaystyle {}_{}}$ ${\displaystyle \mathbf {n}$ = ($n_{1},n_{2},n_{3})}$의 경우 다음에서 올바른 각도를 얻을 수 있습니다$.$

${\displaystyle \left\{\begin {matrix}\cos \theta &=&{\dfrac {tr}(R)-1}{2}\sin \theta &=&-{\dfrac {\operatorname {tr}(K_{n}R)}{2}\end{matrix}}\right.}$

어디에

${\displaystyle K_{n}={\begin{bmatrix}0&-n_{3}&n_{2}\\n_{3}&0&-n_{1}\\-n_{2}&n_{1}&0\\\end{bmatrix}}}$

축 및 각도에서 회전 행렬

u + u + u = 1인 단위 벡터인 u = (u, u, u) 축을 중심으로 각도 θ에 의한 적절한 회전 R의 행렬은 다음과 같습니다.

${\displaystyle R={\begin{bmatrix}\cos \theta +u_{x}^{2}\left(1-\cos \theta \right)&u_{x}u_{y}\left(1-\cos \theta \right)-u_{z}\sin \theta &u_{x}u_{z}\left(1-\cos \theta \right)+u_{y}\sin \theta \u_{y}u_{x}\left(1-\cos \theta \right)+u_{z}\sin \right \theta \\u_{z}u_{x}\left(1-\cos \theta \right)-u_{y}\sin \theta &u_{z}u_{y}\left(1-\cos \theta \right)+u_{x}\sin \theta &\cos \theta +u_{z}^{2}\left(1-\cos \theta \right)\end{bmatrix}}.}$

이 행렬의 첫 번째 원리에서 파생된 것은 여기 섹션 9.2에서 확인할 수 있습니다.^[9] 이 행렬을 도출하기 위한 기본 아이디어는 문제를 알려진 몇 가지 간단한 단계로 나누는 것입니다.

1. 먼저 주어진 축과 해당 축이 좌표 평면(xy, yz 또는 zx) 중 하나에 있도록 점을 회전합니다.
2. 그런 다음 주어진 축과 해당 축이 해당 특정 좌표 평면(x, y 또는 z)에 대한 두 좌표 축 중 하나와 정렬되도록 점을 회전합니다.
3. 기본 회전 행렬 중 하나를 사용하여 회전축이 정렬된 좌표축에 따라 점을 회전시킵니다.
4. 축-점 쌍을 역회전하여 2단계에서와 같은 최종 구성에 도달합니다(2단계 실행 해제).
5. 1단계에서 수행한 축-점 쌍을 역회전합니다(1단계 실행 해제).

이것은 다음과 같이 간결하게 쓸 수 있습니다.

${\displaystyle R=(\cos \theta )\,I+(\sin \theta )\,[\mathbf {u}]_{\times }+(1-\cos \theta )\,(\mathbf {u} \otimes \mathbf {u}),}$

여기서 [u]는 u의 교차 곱 행렬이고, u ⊗ u는 외부 곱이고, I는 항등 행렬입니다. 또는 행렬 항목은 다음과 같습니다.

${\displaystyle R_{jk}={\begin{cases}\cos ^{2}{\frac {\theta }{2}}+\sin ^{2}{\frac {\theta }{2}}\left(2u_{j}^{2}-1\right),\quad &{\text{if }}j=k\\2u_{j}u_{k}\sin ^{2}{\frac {\theta }{2}}-\varepsilon _{jkl}u_{l}\sin \theta ,\quad &{\text{if }}j\neq\end{case}}$

여기서 ε는 ε = 1인 레비-시비타 기호입니다. 이것은 로드리게스의 회전 공식(또는 동등하고, 상이하게 매개변수화된 오일러-로드리게스 공식)의^{[nb 2]} 행렬 형식입니다.

${\displaystyle \mathbf {u} \otimes \mathbf {u} =\mathbf {u} \mathbf {u} ^{\mathsf {T}}={\begin{bmatrix}u_{x}^{2}&u_{x}u_{y}&u_{x}u_{z}\\[3pt]u_{x}u_{y}&u_{y}^{2}&u_{y}u_{z}\\[3pt]u_{x}u_{z}&u_{y}u_{z}&u_{z}^{2}\end{bmatrix}},\qquad [\mathbf {u} ]_{\times }={\begin{bmatrix}0&-u_{z}&u_{y}\\[3pt]u_{z}&0&-u_{x}\\[3pt]-u_{y}&u_{x}&0\end{bmatrix}}.}$

${\displaystyle {}^{}}$ ${\displaystyle \mathbb {R} ^{3}}$에서 벡터 x가 축 u를 중심으로 각도 θ에 의해 회전하는 것은 다음과 같이 쓸 수 있습니다.

${\displaystyle R_{\mathbf {u} }(\theta)\mathbf {x} =\mathbf {u}(\mathbf {u} \cdot \mathbf {x}) +\cos \left(\theta \right)(\mathbf {u} \times \mathbf {x})\times \mathbf {u} +\sin \left(\theta \right)(\mathbf {u})}$

또는 동등하게:

${\displaystyle R_{\mathbf {u} }(\theta)\mathbf {x} =\mathbf {x} \cdot \mathbf {u}(1-\cos(\theta))-\mathbf {x} \times \mathbf {u} \sin {\theta }$

이것은 텐서 표기법으로 다음과 같이 쓸 수도 있습니다.^[11]

${\displaystyle (R_{\mathbf {u} }(\theta )\mathbf {x})_{i}(R_{\mathbf {u} }(\theta )_{ij}{\mathbf {x} }_{j}\text{with}\mathbf {u}(\theta )_{ij} =\delta _{ij}\cos(\theta )+\mathbf {u} _{i}\mathbf {u} _{j}(1-\cos(\cos(\theta)\cos(\mathbf {u})$

3D 공간이 오른손잡이이고 θ > 0인 경우 관찰자를 가리킬 때 이 회전은 시계 반대 방향입니다(우측 규칙). 명시적으로$,{\displaystyle }$ (${\displaystyle \alpha \mathit{},}$ ${\displaystyle \beta \mathit{},}$ ${\displaystyle u\mathbf{})}$ ${\displaystyle({\boldsymbol {\alpha}},$ {\$boldsymbol {\beta},\mathbf {u})}$을(를) 오른손 직교 기저로,

${\displaystyle R_{\mathbf {u}}(\theta){\bold 기호 {\alpha }=\cos \left(\theta \right){\bold 기호 {\alpha }+\sin \left(\theta \right){\bold 기호 {\beta }},\quad R_{\mathbf {u}}(\theta){\bold 기호 {\beta }=-\sin \left(\theta \right){\bold 기호 {\alpha }}+\cos \left(\theta \right){\bold 기호}\quad R_{\mathbf {u} }(\theta )\mathbf {u} =\mathbf {u} .}$

아래의 동등한 Lie-대수 공식과 현저한 차이를 주목하십시오.

특성.

${\displaystyle {}^{}}$에 작용하는 임의의 n차원 회전 행렬 R에 대하여${\displaystyle {}^{}}$ ${\displaystyle \mathbb {R} ^{n}$

${\displaystyle {}^{}{}^{}}$ $=$ R${\displaystyle {}^{}}$- ${\displaystyle 1^{}}$ ${\displaystyle$ R$^{\math$T}=$R^{-1}}($회전은 직교 행렬)

다음과 같습니다.

${\displaystyle \det R=\pm 1}$

회전은 detR = 1이면 적합(또는 회전 반사), detR = – 1이면 부적절(또는 회전 반사)이라고 합니다. 짝수 차원 n = 2k의 경우, 적절한 회전의 n개의 고유값 λ은 통일성의 근인 복소 켤레의 쌍으로 발생합니다: j = 1, ..., k는 λ = ±1에 대해서만 참인 λ = e입니다. 따라서 회전에 의해 고정된 벡터가 없을 수 있으며(λ =1), 따라서 회전축이 없을 수 있습니다. 고정된 고유 벡터는 쌍으로 발생하며, 회전축은 짝수 차원의 부분 공간입니다.

홀수 차원 n = 2k + 1인 경우 적절한 회전 R은 홀수 수의 고유값을 가지며 적어도 하나의 λ = 1이고 회전축은 홀수 차원 부분 공간이 됩니다. 증명:

${\displaystyle {\begin{aligned}\det \left(R-I\right)&=\det \left(R^{\mathsf {T}\right)\det \left(R-I\right)=\det \left(R^{\mathsf {T}}R-R^{\mathsf {T}}\right)=\det \left (I-R^{\mathsf {T}\right)\\&=\det(I-R)=\left(-1\right)^{n}\det \left(R-I\right)=-\det \left(R-I\right).\end{align}}$

여기서 I는 항등 행렬이며 n이 홀수이므로 det(R) = det(R) = 1뿐만 아니라 (-1) = -1도 사용합니다. 따라서 det(R – I) = 0, 즉 고정 고유 벡터인 (R – I)v = 0인 널 벡터 v가 있음을 의미합니다. 또한 v와 직교하는 짝수 차원 부분 공간에는 고정된 고유 벡터 쌍이 있을 수 있으므로 고정된 고유 벡터의 전체 차원은 홀수입니다.

예를 들어, 2-공간 n = 2에서 각도 θ에 의한 회전은 고유값 λ = e와 λ = e를 가지므로 널 회전의 경우인 θ = 0일 때를 제외하고는 회전축이 없습니다. 3-공간 n = 3에서 null이 아닌 고유 회전의 축은 항상 고유선이며, 각도 θ에 의한 이 축을 중심으로 한 회전은 고유값 λ = 1, e를 갖습니다. 4-공간 n = 4에서 4개의 고유값은 다음과 같은 형태입니다. Null 회전은 θ = φ = 0입니다. θ = 0의 경우, φ ≠ 0은 축면을 이루는 두 개의 단위 고유값과 축면에 직교하는 2차원 회전을 단순 회전이라고 합니다. 그렇지 않으면 축면이 없습니다. θ =φ의 경우를 등사선 회전이라고 하며, 고유값 e가 두 번 반복되므로 모든 벡터는 각도 θ을 통해 회전됩니다.

회전 행렬의 흔적은 고유값의 합과 같습니다. n = 2인 경우 각도 θ에 의한 회전은 트레이스 2 코스 θ를 갖습니다. n = 3인 경우 각도 θ에 의한 축 주위의 회전은 트레이스 1 + 2 코스 θ을 갖습니다. n = 4인 경우, 트레이스는 2(cos θ + cos φ)이며, 이는 등사선 회전의 경우 4 cos θ가 됩니다.

예

기하학.

유클리드 기하학에서 회전은 등각도의 한 예로, 점들 사이의 거리를 변경하지 않고 점들을 이동시키는 변환입니다. 회전은 두 개의 추가적인 특성에 의해 다른 등각선과 구별됩니다. (적어도) 하나의 점을 고정하고 "손잡이"를 변경하지 않습니다. 반대로, 번역은 모든 지점을 이동하고, 반사는 왼손과 오른손 순서를 교환하며, 활공 반사는 양쪽을 모두 수행하며, 부적절한 회전은 손의 변화와 일반 회전을 결합합니다.

고정된 점을 직각좌표계의 원점으로 삼으면 모든 점에 원점으로부터의 변위로 좌표를 부여할 수 있습니다. 따라서 점 자체 대신 변위 벡터 공간으로 작업할 수 있습니다. 이제 (p₁, ..., p_n)를 원점 O에서 점 P까지의 벡터 p의 좌표라고 가정합니다. 우리의 좌표에 대한 정규적인 기저를 선택하고, 피타고라스에 의해 P까지의 거리의 제곱은

${\displaystyle d^{2}(O,P)=\ \mathbf {p} \ ^{2}=\sum _{r=1}^{n}p_{r}^{2}}$

행렬 곱셈을 사용하여 계산할 수 있습니다.

${\displaystyle \ \ \mathbf {p} \ ^{2} = {\begin{bmatrix} p_{1}\cdots p_{n}\end{bmatrix} p_{1}\\\vdots \\p_{n}\end{bmatrix}} =\mathbf {p} ^{\mathsf {T}\mathbf {p} .}$

기하학적 회전은 선을 선으로 변환하고 점 사이의 거리 비율을 보존합니다. 이러한 특성으로부터 회전은 벡터의 선형 변환이므로 행렬 형태인 Qp로 작성할 수 있음을 알 수 있습니다. 회전이 비율뿐만 아니라 거리 자체를 보존한다는 사실은 다음과 같이 기술됩니다.

${\displaystyle \mathbf {p} ^{\mathsf {T}\mathbf {p} = (Q\mathbf {p})^{\mathsf {T}(Q\mathbf {p}),}$

또는

${\displaystyle {\begin{aligned}\mathbf {p} ^{\mathsf {T}I\mathbf {p} & {}=\left(\mathbf {p} ^{\mathsf {T}\right)(Q\mathbf {p})\&{}=\mathbf {p} ^{\mathsf {T}\left(Q^{\mathsf {T} Q\right)\mathbf {p} .\end{align}}}$

이 방정식은 모든 벡터에 대해 성립하기 때문에 모든 회전 행렬 Q가 직교 조건을 만족한다는 결론을 내립니다.

${\displaystyle Q^{\mathsf {T}Q=I.}$

회전은 특수 행렬 조건을 암시하는 축의 순서를 변경할 수 없으므로 손의 균형을 유지하고,

${\displaystyle \det Q=+1.}$

마찬가지로 중요한 것은 이 두 조건을 만족하는 모든 행렬이 회전으로 작용한다는 것을 보여줄 수 있습니다.

곱셈

회전행렬의 역수는 전치행렬이며, 이는 회전행렬이기도 합니다.

${\displaystyle {\begin{align}\left(Q^{\mathsf {T}\right)^{\mathsf {T}\left(Q^{\mathsf {T}\right)&=QQ^{\mathsf {T}=I\\\det Q^{\mathsf {T}&=\det Q=+1.\end{align}}$

두 회전행렬의 곱은 다음과 같은 회전행렬입니다.

${\displaystyle {\begin{align}\left(Q_{1}Q_{2}\right)^{\mathsf {T}\left(Q_{1}Q_{2}\right)&=Q_{2}^{\mathsf {T}}\left(Q_{1}^{\mathsf {T}}Q_{1}\right)Q_{2}=I\\\det \left(Q_{1}Q_{2}\right)&=\left(\det Q_{1}\right)\left(\det Q_{2}\right)=+1.\end{align}}$

n > 2인 경우 n × n 회전 행렬의 곱은 일반적으로 가환적이지 않습니다.

${\displaystyle {\begin {aligned}Q_{1}&={\begin{bmatrix}0&-1&0\\1&0&0\\0&0&1\end{bmatrix}}&Q_{2}&={\begin{bmatrix}0&0&1\\0&1&0\\-1&0&0\end{bmatrix}}\\Q_{1}Q_{2}&={\begin{bmatrix}0&-1&0\\0&0&1\\-1&0&0\end{bmatrix}}&Q_{2}Q_{1}&={\begin{bmatrix}0&0&1\\1&0&0\\0&1&0\end{bmatrix}}.\end{align}}$

임의의 항등 행렬은 회전 행렬이고 행렬 곱셈은 연관 행렬이라는 점에 주목하여, n × n 회전 행렬이 하나의 군을 이룬다고 함으로써 이러한 모든 성질을 요약할 수 있는데, n > 2인 경우에는 특수 직교군이라고 하며 SO(n), SO(n,R), SO_n 또는 SO_n(R)로 표시되며, n × n 회전 행렬의 군은 n차원 공간에서의 회전 군과 동형입니다. 이는 회전 행렬의 곱셈이 해당 행렬의 왼쪽에서 오른쪽 순서로 적용되는 회전의 구성에 해당한다는 것을 의미합니다.

애매모호

회전 행렬의 해석에는 많은 모호성이 적용될 수 있습니다.

대부분의 경우 모호성의 효과는 회전 행렬 반전의 효과와 동일합니다(이러한 직교 행렬의 경우 동일한 행렬 전치).

별칭 또는 알리바이(수동 또는 활성) 변환

점 P의 좌표는 좌표계 CS(에일리어스)의 회전 또는 점 P(에일리어스)의 회전에 의해 변경될 수 있습니다. 후자의 경우, P의 회전은 또한 P를 나타내는 벡터 v의 회전을 생성합니다. 즉, CS가 회전하는 동안 P와 v가 고정되거나(알리비아), P와 v가 회전하는 동안 CS가 고정됩니다(알리비아). 주어진 회전은 벡터와 좌표계가 실제로 서로에 대해 동일한 축에 대해 회전하지만 반대 방향으로 회전하기 때문에 두 가지 방법으로 합법적으로 설명할 수 있습니다. 이 기사를 통해 회전을 설명하기 위해 알리바이 접근 방식을 선택했습니다. 예를 들어.

${\displaystyle R(\theta)={\begin{bmatrix}\cos \theta &-\sin \theta &\cos \\end{bmatrix}}$

각도 θ에 의한 벡터 v의 반시계 방향 회전 또는 동일한 각도에 의한 CS의 반대 방향(즉, 시계 방향)의 회전을 나타냅니다. 알리바이와 가명 변환은 각각 능동적 변환과 수동적 변환이라고도 합니다.

사전 곱셈 또는 사후 곱셈

동일한 점 P는 열 벡터 v 또는 행 벡터 w로 나타낼 수 있습니다. 회전 행렬은 열 벡터의 사전 곱셈(Rv) 또는 행 벡터의 사후 곱셈(wR)을 사용할 수 있습니다. 그러나 Rv는 wR에 대해 반대 방향으로 회전을 생성합니다. 이 기사 전체에서 열 벡터에서 생성된 회전은 사전 곱셈을 통해 설명됩니다. 정확히 동일한 회전(즉, 점 P의 동일한 최종 좌표)을 얻으려면 등가 행 벡터에 R(즉, wR^T)의 전치값을 사후 곱해야 합니다.

오른쪽 또는 왼쪽 좌표

행렬과 벡터는 오른손잡이 또는 왼손잡이 좌표계를 기준으로 나타낼 수 있습니다. 기사 전반에 걸쳐 달리 명시되지 않는 한 오른손잡이 방향을 가정했습니다.

벡터 또는 형식

벡터 공간은 선형 형태의 이중 공간을 가지며 행렬은 벡터 또는 형태에 작용할 수 있습니다.

분해

독립 비행기

3 × 3 회전 행렬을 생각해 보십시오.

${\displaystyle Q={\begin{bmatrix}0.36&0.48&-0.80\\-0.80&0.60&0.00\\0.48&0.64&0.60\end{bmatrix}}.}$

Q가 어떤 방향, v, 순수하게 인자 λ에 의한 스케일링으로 작용한다면, 우리는

${\displaystyle Q\mathbf {v} =\lambda \mathbf {v},}$

하도록

${\displaystyle \mathbf {0} = (\lambda I-Q)\mathbf {v} .}$

따라서 λ은 Q에 대한 특성 다항식의 근이며,

${\displaystyle {\begin {align}0&{}=\det(\lambda I-Q)\\&{}=\lambda ^{3}-{\tfrac {39}{25}\lambda ^{2}+{\tfrac {39}{25}\lambda -1\&{}=(\lambda -1)\left(\lambda ^{2}-{\tfrac {14}{25}\lambda +1\right).\end{align}}$

두 가지 기능이 주목할 만합니다. 먼저, 뿌리(또는 고유값) 중 하나는 1인데, 이는 어떤 방향은 행렬의 영향을 받지 않는다는 것을 말해줍니다. 3차원 회전의 경우, 이는 회전의 축(다른 차원에서는 의미가 없는 개념)입니다. 둘째, 나머지 두 근은 복소 켤레이며, 그 곱은 1(2차의 상수항)이고, 그 합은 2cos θ(음의 선형항)입니다. 이 인수분해는 3 × 3 회전 행렬의 경우 모두 동일한 일이 발생하기 때문에 관심이 있습니다. (특수한 경우로, 널 회전의 경우 "복소수 켤레"는 모두 1이고, 180° 회전의 경우 모두 -1입니다.) 또한 모든 n × n 회전 행렬에 대해서도 유사한 인수분해가 유지됩니다. 차원 n이 홀수이면 1의 "당글링" 고유값이 존재하며, 어떤 차원에 대해서도 나머지 다항식 인자는 여기와 같은 2차 항으로 표시됩니다(두 개의 특수한 경우가 있음). 우리는 특성 다항식이 차수가 있고 따라서 n개의 고유값을 가질 것임을 보장합니다. 그리고 회전행렬은 전치행렬로 통근하기 때문에 정규행렬이므로 대각화가 가능합니다. 우리는 적절한 좌표계로 표현될 때 모든 회전 행렬이 최대 n/2개의 2차원 부분 공간의 독립적인 회전으로 분할된다는 결론을 내립니다.

행렬의 주 대각선에 있는 항목의 합을 트레이스라고 하며, 좌표 시스템의 방향을 변경해도 변경되지 않으며 항상 고유값의 합과 같습니다. 이것은 2차원 공간(또는 부분 공간)에서 회전 각도인 θ을 추적이 드러낸다는 2 × 2 및 3 × 3 회전 행렬에 대한 편리한 의미를 갖습니다. 2 × 2 행렬의 경우 추적은 2 cos θ이고 3 × 3 행렬의 경우 1 + 2 cos θ입니다. 3차원의 경우 부분 공간은 회전축에 수직인 모든 벡터(고윳값이 1인 불변 방향)로 구성됩니다. 따라서 우리는 임의의 3×3 회전행렬로부터 회전축과 각도를 추출할 수 있으며, 이것들은 회전을 완전히 결정합니다.

순차각

2 × 2 회전 행렬의 제약 조건은 다음과 같은 형태를 가져야 함을 의미합니다.

${\displaystyle Q={\begin{bmatrix}a&-b\b&a\end{bmatrix}}}$

with a² + b² = 1. 따라서 일부 각도 θ에 대해 = cos θ와 b = sin θ를 설정할 수 있습니다. θ를 해결하기 위해서는 a나 b를 단독으로 보는 것만으로는 충분하지 않습니다. 우리는 두 개의 논법 아크탄젠트 함수를 사용하여 각도를 올바른 사분면에 배치하기 위해 둘을 함께 고려해야 합니다.

이제 3×3 회전행렬의 첫 번째 열을 생각해 보자,

${\displaystyle {\begin{bmatrix}a\b\c\end{bmatrix}}.}$

a² + b는² 아마도 1과 같지 않지만, 어떤 값 r² < 1이지만, 이전 계산의 약간의 변형을 사용하여 열을 다음과 같이 변환하는 소위 기븐스 회전을 찾을 수 있습니다.

${\displaystyle {\begin{bmatrix}r\\0\c\end{bmatrix}},}$

제로잉 b 이것은 x축과 y축에 걸쳐 있는 부분 공간에 작용합니다. 그런 다음 xz 부분 공간에 대한 프로세스를 0 c로 반복할 수 있습니다. 이 두 회전은 전체 행렬에 작용하여 도식적 형태를 생성합니다.

${\displaystyle Q_{xz}Q_{xy}Q={\begin{bmatrix}1&0&0\\0&\ast &\ast \\0&\ast &\ast \end{bmatrix}}.}$

두 번째 열로 주의를 이동하면 yz-하위 공간의 기븐스 회전으로 이제 z 값이 0이 될 수 있습니다. 이를 통해 전체 행렬이 양식에 표시됩니다.

${\displaystyle Q_{yz}Q_{xz}Q_{xy}Q={\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}},}$

아이덴티티 매트릭스입니다. 그래서 Q를 분해했습니다.

${\displaystyle Q=Q_{xy}^{-1}Q_{xz}^{-1}Q_{yz}^{-1}.}$

n × n 회전 행렬은 (n - 1) + (n - 2) + ⋯ + 2 + 1, 또는

${\displaystyle \sum _{k=1}^{n-1}k={\frac {1}{2}}n(n-1)}$

대각선 아래의 0. 우리는 고정된 평면 순서로 일련의 회전으로 기둥을 밟는 것과 같은 아이디어를 확장함으로써 그들을 0으로 만들 수 있습니다. 우리는 각각 n개의² 엔트리를 갖는 n × n 회전 행렬의 집합이 1/2n(n - 1) 각도로 매개변수화될 수 있다는 결론을 내립니다.

xzxw	시큰둥한w	xxxw	xyzw
yxyw	yxzw	이찌의w	yzxw
쫀득쫀득한w	징크스w	zxzw	zxyw
xzxb	yzxb	xxxb	징크스b
yxyb	zxyb	이찌의b	시큰둥한b
쫀득쫀득한b	xyzb	zxzb	yxzb

3차원에서 이것은 행렬에서 오일러에 의해 만들어진 관측을 형성하므로 수학자들은 3개의 각도로 이루어진 순서열을 오일러 각도라고 부릅니다. 하지만 지금까지 저희가 지적했던 것보다 상황이 다소 복잡합니다. 작은 치수에도 불구하고 우리는 실제로 우리가 사용하는 축 쌍의 순서에서 상당한 자유를 가지고 있고, 또한 각도를 선택하는 데 있어서도 약간의 자유를 가지고 있습니다. 따라서 우리는 3차원 회전이 물리학, 의학, 화학 또는 다른 학문에 대해 매개변수화될 때 사용되는 많은 다양한 규칙을 발견합니다. 월드 축 또는 바디 축의 옵션을 포함하면 24개의 다른 시퀀스가 가능합니다. 그리고 어떤 학문은 어떤 수열도 오일러 각도라고 부르는 반면, 다른 학문은 다른 수열에 다른 이름(카르다노, 테이트-브라이언, 롤-피치-요)을 부여합니다.

옵션 수가 많은 한 가지 이유는 앞서 언급한 바와 같이 3차원(및 그 이상)의 회전이 통근하지 않기 때문입니다. 주어진 회전 수열을 반대로 하면 다른 결과를 얻을 수 있습니다. 이것은 또한 우리가 그들의 대응하는 각도를 더해서 두 회전을 구성할 수 없다는 것을 의미합니다. 따라서 오일러 각도는 수들의 삼중항과 외관상 유사함에도 불구하고 벡터가 아닙니다.

중첩 치수

다음과 같은 3×3 회전 행렬

${\displaystyle Q_{3\times 3}={\begin {bmatrix}\cos \theta &-\sin \theta & {\color {CadetBlue}0}\\sin \theta & {\color {CadetBlue}0}\{\color {CadetBlue}0}&{\color {CadetBlue}0}&{\color {CadetBlue}1}\end{bmatrix}}}$

2 × 2 회전 행렬을 제안합니다.

${\displaystyle Q_{2\times 2}={\begin{bmatrix}\cos \theta &-\sin \theta &\cos \end{bmatrix}},}$

는 왼쪽 상단 모서리에 내장되어 있습니다.

${\displaystyle Q_{3\times 3}=\left[{\begin{matrix}Q_{2\times 2}&\mathbf {0} \\mathbf {0} ^{\mathsf {T}&1\end{matrix}}\right}}$

이것은 환상이 아닙니다. n차원 회전의 하나만이 아니라 많은 사본이 (n + 1)차원 회전 내에서 하위 그룹으로 발견됩니다. 각 임베딩은 한 방향을 고정한 상태로 유지하며, 이 방향은 3 × 3 행렬의 경우 회전축입니다. 예를 들어, 우리는

${\displaystyle {\begin {aligned}Q_{\mathbf {x} }(\theta) & ={\begin {bmatrix}{\color {CadetBlue}0}&{\color {CadetBlue}0}\{\color {CadetBlue}0}&\cos \theta &-\sin \theta \\{\color {CadetBlue}0}&\sin \theta &\cos \end{bmatrix},\\[8px]Q_{\mathbf {y} }(\theta) & ={\begin {bmatrix}\cos \theta & {\color {CadetBlue}0}&\sin \theta \\{\color {CadetBlue}0}&{\color {CadetBlue}0}\-\sin \theta & {\color {CadetBlue}0}&\cos \end{bmatrix},\\[8px]Q_{\mathbf {z} }(\theta)&={\begin {bmatrix}\cos \theta &-\sin \theta &{\color {CadetBlue}0}\\sin \theta &\cos \theta &{\color {CadetBlue}0}\\{\color {CadetBlue}0}&{\color {CadetBlue}0}\{\color {CadetBlue}1}\end{bmatrix}},\end{aligned}}}$

x축, y축 및 z축을 각각 고정합니다. 회전축은 반드시 좌표축일 필요는 없으며, u = (x,y,z)가 원하는 방향의 단위 벡터인 경우,

${\displaystyle {\begin {aligned}Q_{\mathbf {u} }(\theta )&={\begin{bmatrix}0&-z&y\\z&0&-x\\-y&x&0\end{bmatrix}}\sin \theta +\left(I-\mathbf {u} \mathbf {u} ^{\mathsf {T}}\right)\cos \theta +\mathbf {u} \mathbf {u} ^{\mathsf {T}}\\[8px]&={\begin{bmatrix}\left(1-x^{2}\right)c_{\theta }+x^{2}&-zs_{\theta }-xyc_{\theta }+xy&ys_{\theta }-xzc_{\theta }+xz\\zs_{\theta }-xyc_{\theta }+xy&\left(1-y^{2}\right)c_{\theta }+y^{2}&-xs_{\theta }-yzc_{\theta }+yz\\-ys_{\theta }-xzc_{\theta }+xz&xs_{\theta }-yzc_{\theta }+yz&\left(1-z^{2}\right)c_{\theta }+z^{2}\end{bmatrix}}\\[8px]&={\begin{bmatrix}x^{2}(1-c_{\theta })+c_{\theta }&xy(1-c_{\theta })-zs_{\theta }&xz(1-c_{\theta })+ys_{\theta }\\xy(1-c_{\theta })+zs_{\theta }&y^{2}(1-c_{\theta })+c_{\theta }&yz(1-c_{\theta })-xs_{\theta }\\xz(1-c_{\theta })-ys_{\theta }&yz(1-c_{\theta })+xs_{\theta }&z^{2}(1-c_{\theta })+c_{\theta }\end{bmatrix}},\end{aligned}}}$

여기서 c = cos θ, s = sin θ는 각도 θ에 의한 회전으로 축이 고정된 상태로 있습니다.

(n + 1)차원 공간의 방향은 일반화된 구 Sⁿ 위의 한 점을 고려할 수 있는 단위 크기 벡터가 될 것입니다. 따라서 회전군 SO(n + 1)는 SO(n)와 S를ⁿ 결합한 것으로 설명하는 것이 당연합니다. 적절한 형식주의는 섬유 다발입니다.

${\displaystyle SO(n)\hook 오른쪽 화살표 SO(n+1)\toS^{n}}$

여기서 기저 공간의 모든 방향에 대해 전체ⁿ 공간에서 S, SO(n + 1) 위의 섬유는 섬유 공간, SO(n)의 복사, 즉 방향을 고정하는 회전입니다.

따라서 2×2 행렬로 시작하여 고정축을² S(3차원 공간의 일반 구)에, 그 결과 회전을 S에³ⁿ⁻¹ 조준하여 n×n 회전 행렬을 구축할 수 있습니다. S 위의ⁿ 한 점은 n개의 수를 사용하여 선택할 수 있으므로, n×n 회전 행렬을 설명하기 위해 다시 1/2n(n - 1)개의 수를 갖게 됩니다.

사실, 우리는 앞에서 설명한 순차적 각도 분해를 이 과정을 뒤집는 것으로 볼 수 있습니다. n - 1 기븐스 회전의 구성은 첫 번째 열(및 행)을 (1, 0, ..., 0)으로 가져오므로 행렬의 나머지는 (1, 0, ..., 0)을 고정 상태로 두도록 내장된 1차원 미만의 회전 행렬입니다.

케일리 공식을 통한 스큐 모수

n × n 회전 행렬 Q가 -1 고유값을 포함하지 않으므로, 그것이 구성하는 평면 회전 중 어느 것도 180° 회전하지 않을 때, Q + I는 가역 행렬입니다. 대부분의 회전 행렬은 이 설명에 적합하며, 이들에 대해 (Q - I)(Q + I)⁻¹은 스큐 대칭 행렬인 A임을 알 수 있습니다. 따라서 A = -A이고 대각선이 반드시 0이고 위쪽 삼각형이 아래쪽 삼각형을 결정하기 때문에 A는 1/2n(n - 1)개의 독립적인 숫자를 포함합니다.

편리하게도 I - A는 비대칭일 때마다 가역이므로 케일리 변환을 사용하여 원래 행렬을 복구할 수 있습니다.

${\displaystyle A\maps to (I+A)(I-A)^{-1}}$

스큐 대칭 행렬 A를 회전 행렬에 매핑합니다. 사실, 언급된 예외를 제외하고는 이러한 방식으로 모든 회전 행렬을 생성할 수 있습니다. 실제 응용 분야에서는 180° 회전을 무시할 여유가 거의 없지만 케일리 변환은 삼각 함수가 없는 대부분의 회전 행렬의 매개 변수화를 제공하는 잠재적으로 유용한 도구입니다.

예를 들어, 우리는 3차원적으로 (Cayley 1846)

${\displaystyle {\begin{aligned}&{\begin{bmatrix}0&-z&y\\z&0&-x\\-y&x&0\end{bmatrix}}\mapsto \\[3pt]\quad {\frac {1}{1+x^{2}+y^{2}+z^{2}}}&{\begin{bmatrix}1+x^{2}-y^{2}-z^{2}&2xy-2z&2y+2xz\\2xy+2z&1-x^{2}+y^{2}-z^{2}&2yz-2x\\2xz-2y&2x+2yz&1-x^{2}-y^{2}+z^{2}\end{bmatrix}}.\end{align}}$

스큐 항목을 벡터(x,y,z)로 압축하면 (1,0,0)의 경우 x축을 중심으로, (0,1,0)의 경우 y축을 중심으로, (0,0,1)의 경우 z축을 중심으로 90° 회전합니다. 180° 회전은 도달할 수 없습니다. x → ∞의 한계에서 (x, 0, 0)은 x 축을 중심으로 180° 회전에 접근하며, 다른 방향에서도 마찬가지입니다.

전단으로 분해

2D의 경우, 회전 행렬은 세 개의 전단 행렬로 분해될 수 있습니다(Paeth 1986).

${\displaystyle {\begin{align}R(\theta)&{}={\begin{bmatrix}1&-\tan {\frac {\theta}{2}}\\0&1\end{bmatrix}}{\theta &1\end{bmatrix}}{\begin{bmatrix}1&-\tan {\frac {\theta}{2}\\0&1\end{bmatrix}}\end{align}}}$

예를 들어, 이것은 비트맵을 직접 회전하는 것보다 적은 수의 곱셈 명령으로 전단기를 구현할 수 있기 때문에 컴퓨터 그래픽에서 유용합니다. 현대 컴퓨터에서는 이것이 중요하지 않을 수 있지만 매우 오래되거나 보급형 마이크로프로세서에 관련될 수 있습니다.

회전은 두 개의 전단기와 스케일링으로 작성될 수도 있습니다(Daubechies & Sweldens 1998).

${\displaystyle {\begin{align}R(\theta)&{}={\begin{bmatrix}1&0\\tan \theta & 1\end{bmatrix}}{\begin{bmatrix}1&-\sin \theta \cos \0&1\end{bmatrix}{\begin{bmatrix}}\cos \theta & 0\0&{\frac {1}{\cos \theta }}\end{bmatrix}}}$

군론

아래는 수학 및 특히 회전 대칭이 모든 진정한 기본 법칙의 요구 사항인 물리학에서 고정 차원(여기서는 대부분 3)의 모든 회전 행렬 집합의 역할에 대한 몇 가지 기본 사실을 따릅니다(공간의 등방성 가정으로 인해). 그리고 동일한 대칭이 존재할 때, 는 덜 근본적인 성격의 많은 문제를 단순화하는 속성입니다. 고전역학과 양자역학에 그 예가 많습니다. 이 대칭과 관련된 솔루션 부분에 대한 지식은 이러한 모든 문제에 적용되며, 당면한 특정 문제를 고려할 수 있으므로 복잡성을 줄일 수 있습니다. 수학과 물리학의 대표적인 예는 구형 고조파 이론일 것입니다. 회전 그룹의 그룹 이론에서 그들의 역할은 회전 그룹 SO(3)의 유한 차원 축소 불가능한 표현 집합 전체에 대한 표현 공간이 되는 것입니다. 이 항목은 회전 그룹 SO(3) § 구형 고조파를 참조하십시오.

자세한 내용은 각 섹션에 나열된 주요 기사를 참조하십시오.

거짓말단

각 n에 대한 n × n 회전 행렬은 특별한 직교 그룹인 SO(n) 그룹을 형성합니다. 이 대수적 구조는 곱셈과 역수를 취하는 연산이 행렬 항목의 분석 함수가 되도록 ${\displaystyle GLn}$⁡(R) ${\displaystyle \operatorname {GL$} _{$n}(\mathbb {$R})}에서 상속된 위상 구조와 결합됩니다. 따라서 SO(n)은 각 거짓말 그룹에 대한 것입니다. 컴팩트하고 연결되어 있지만 단순히 연결되지는 않습니다. 또한 SO(4)를 예외로 하는 반단순 그룹입니다.^[12] 이것의 관련성은 분석 다양체 이론(해석 다양체는 특히 매끄러운 다양체)의 모든 정리와 모든 기계가 적용되며, 잘 개발된 소형 반단순 그룹의 표현 이론을 사용할 준비가 되어 있다는 것입니다.

리 대수

SO(n)의 리 대수 so(n)는 다음과 같이 주어집니다.

${\displaystyle {\mathfrak {so}}(n)={\mathfrak {o}(n)=\left\{X\in M_{n}(\mathbb {R})\mid X=-X^{\mathsf {T}\right\},}$

는 차원 n의 스큐-대칭 행렬의 공간이며, 고전군을 참조하면, 여기서 o(n)은 직교군인 O(n)의 리 대수입니다. 참고로, so(3)의 가장 일반적인 근거는

${\displaystyle L_{\mathbf {x} }={\begin{bmatrix}0&0&0\\0&0&-1\\0&1&0\end{bmatrix}},\quad L_{\mathbf {y} }={\begin{bmatrix}0&0&1\\0&0&0\\-1&0&0\end{bmatrix}},\quad L_{\mathbf {z} }={\begin{bmatrix}0&-1&0\\1&0&0\\0&0&0\end{bmatrix}}.}$

지수도

Lie 대수를 Lie 그룹에 연결하는 것은 지수 맵이며, 이는 e에^A[13] 대한 표준 행렬 지수 급수를 사용하여 정의됩니다. 임의의 스큐 대칭 행렬 A에 대해 exp(A)는 항상 회전 행렬입니다.^{[nb 3]}

중요한 실제 사례는 3×3 케이스입니다. 회전 그룹 SO(3)에서는 오일러 벡터 ω = θ u로 모든 A ∈ so(3)를 식별할 수 있음을 보여주며, 여기서 u = (x, y, z)는 단위 크기 벡터입니다.

식별 ${\displaystyle {}^{}}$(${\displaystyle 2)}$ ≅ $R3 {\displaystyle \mathbf {su$} (2$)\cong \mathbbb${R$\}$ ^{3}}의 속성에 의해 u는 A의 널 공간에 있습니다. 따라서 u는 exp(A)에 의해 불변으로 유지되므로 회전축입니다.

행렬 형식에 대한 로드리게스의 회전 공식에 따르면, 다음을 얻습니다.

${\displaystyle {\begin{align}\exp(A)&=\exp {\bigl(}\theta(\mathbf {u} \cdot \mathbf {L}){\bigr}}\&=\exp \left ({\begin {bmatrix}0&-z\theta & y\theta \\z\theta & 0&-x\theta \\-y\theta & x\theta & 0\end{bmatrix}}\right)\\&=I+\sin \theta \mathbf {u} \cdot \mathbf {L} +(1-\cos \theta )(\mathbf {u} \cdot \mathbf {L})^{2},\end{align}}}$

어디에

${\displaystyle \mathbf {u} \cdot \mathbf {L} ={\begin{bmatrix}0&-z&y\\z&0&-x\\-y&x&0\end{bmatrix}}.}$

이것은 각도 θ에 의한 축 u 주위의 회전에 대한 행렬입니다. 자세한 내용은 지수 지도 SO(3)를 참조하십시오.

베이커-캠벨-하우스도르프 공식

BCH 공식은 X 및 Y의 중첩 정류자의 직렬 확장 측면에서 Z = log(ee)에 대한 명시적인 표현을 제공합니다. 이 일반적인 확장은 다음과^{[nb 4]} 같이 펼쳐집니다.

${\displaystyle Z=C(X,Y)=X+Y+{\tfrac {1}{2}}[X,Y]+{\tfrac {1}{12}}{\bigl [}X,[X,Y]{\bigr ]}-{\tfrac {1}{12}}{\bigl [}Y,[X,Y]{\bigr ]}+\cdots .}$

3×3의 경우, 일반적인 무한 확장은 콤팩트한 형태를 갖지만,^[15]

${\displaystyle Z=\alpha X+\beta Y+\gamma [X,Y],}$

적합한 삼각 함수 계수의 경우 SO(3)에 대한 Baker-Campbell-Hausdorff 공식에 자세히 설명되어 있습니다.

위의 내용은 그룹 아이덴티티로서 더 간단한 더블릿(스피너 표현)을 포함한 모든 충실한 표현에 적용됩니다. 따라서 동일한 명시적 공식은 파울리 행렬을 통해 바로 이어집니다. SU(2)에 대한 2 × 2 도함수를 참조하십시오. 일반적인 n × n의 경우에는 Ref를 사용할 수 있습니다.^[16]

스핀군

n × n 회전 행렬의 Lie 군, SO(n)는 단순히 연결되지 않으므로 Lie 이론은 보편적 피복 군의 동형 이미지임을 알려줍니다. 종종 이 경우 Spin(n)으로 표시되는 스핀 그룹이라고 하는 피복 그룹은 작업하기에 더 간단하고 더 자연스럽습니다.^[17]

평면 회전의 경우 SO(2)는 위상적으로 원, S입니다¹. 이 보편적 피복 그룹인 Spin(2)은 덧셈 중인 실수선 R과 동형입니다. 임의 크기의 각도를 사용할 때마다 범용 커버의 편리함을 활용하는 것입니다. 모든 2 × 2 회전 행렬은 2 π의 정수배로 분리된 셀 수 있는 무한한 각도로 생성됩니다. 이에 따라 SO(2)의 기본군은 정수 Z와 동형입니다.

공간 회전의 경우 SO(3)는 위상학적으로 3차원 실제 투영 공간인 RP와³ 동등합니다. 그것의 보편적인 덮개 그룹인 Spin(3)은 3-구, S와³ 동형입니다. 모든 3×3 회전 행렬은 구 위의 두 개의 반대점에 의해 생성됩니다. 이에 따라 SO(3)의 기본군은 2원소 군인₂ Z와 동형입니다.

우리는 또한 Spin(3)을 곱셈에 따른 단위 노름의 4분의 1, 또는 특정 4 × 4 실수 행렬 또는 2 × 2 복잡한 특수 유니터리 행렬, 즉 SU(2)와 동형으로 설명할 수 있습니다. 첫 번째 경우와 마지막 경우의 표지 지도는 다음과 같습니다.

${\displaystyle \mathbb {H} \supset \{q\in \mathbb {H} :\ q\ = 1\}\ni w+\mathbf {i} x+\mathbf {j} y+\mathbf {k} z\mapsto {\begin{bmatrix}1-2y^{2}-2z^{2}&2xy-2zw&2xz+2yw\\2xy+2zw&1-2x^{2}-2z^{2}&2yz-2xw\\2xz-2yw&2yz+2xw&1-2x^{2}-2y^{2}\end{bmatrix}}\in \mathrm {SO} (3),}$

그리고.

${\displaystyle \mathrm {SU} (2)\ni {\alpha{bmatrix}\alpha & beta \\-{\overline {\alpha}}&{\overline {\alpha }}\end{bmatrix}}\maps to {\alpha{bmatrix}{\frac {1}{2}}\left(\alpha ^{2}-{\alpha ^{2}}+{\overline {\beta ^{2}}}\right)&{\frac {i}{2}}\left (-\alpha ^{2}-\beta ^{2}+{\alpha ^{2}} ^{2}}\right)&-\alpha \beta -{\overline {\alpha }}{\overline {\beta }}\{\frac {i}{2}}\left(\alpha ^{2}-{\overline {\alpha ^{2}}}+{\overline {\beta ^{2}}\right)&{\frac {i}{2}}\left(\alpha ^{2}+\beta ^{2}+{\overline {\alpha ^{2}}}+{\overline {\alpha ^{2}}}\" }}\right)\\alpha {\overline {\beta }+{\overline {\alpha }}\beta &i\left(-\alpha {\overline }+{\alpha }\beta \right)&\alpha {\overline {\alpha }}-\beta {\overline {\bmatrix}}\in \mathrm {SO}(3).}$

SU(2)-커버링 및 4음이온 커버링에 대한 자세한 설명은 스핀 그룹 SO(3)를 참조하십시오.

이러한 케이스의 많은 기능은 더 높은 차원에서도 동일합니다. 커버링은 모두 2대 1이며 SO(n), n > 2이며 기본 그룹 Z가₂ 있습니다. 이러한 그룹의 자연스러운 설정은 클리포드 대수 내에 있습니다. 회전의 한 유형의 동작은 qvq로^∗ 표시되는 일종의 "샌드위치"에 의해 생성됩니다. 물리학 응용 분야에서 더 중요한 것은 리 대수의 해당 스핀 표현이 클리포드 대수의 내부에 있다는 것입니다. 회전 그룹의 투영 표현이라고도 하는 2값 표현을 생성하는 일반적인 방법으로 지수화할 수 있습니다. SO(3)와 SU(2)의 경우가 여기서 2값 표현은 커버링 맵의 "역"으로 볼 수 있습니다. 지도를 덮는 속성을 통해 역을 로컬 섹션으로 일대일로 선택할 수 있지만 전역적으로 선택할 수는 없습니다.

무한소회전

리 대수의 행렬은 회전 자체가 아닙니다. 스큐 대칭 행렬은 도함수, 회전의 비례 차이입니다. 실제 "미분 회전" 또는 무한소 회전 행렬은 다음과 같은 형태를 갖습니다.

${\displaystyle I+A\,d\theta,}$

예를 들어, A = L인 경우, d θ이 거의 작고 A ∈ so(n)인 경우,

${\displaystyle dL_{x}={\begin{bmatrix}1&0&0\\0&1&-d\theta \\0&d\theta &1\end{bmatrix}}.}$

계산 규칙은 2차의 무한소가 일상적으로 떨어지는 것을 제외하고는 평소와 같습니다. 이러한 규칙을 사용하면 이러한 행렬은 일반적인 무한소 처리 하에서 일반적인 유한 회전 행렬과 동일한 속성을 모두 만족하지 못합니다.^[18] 무한소 회전이 적용되는 순서는 무관한 것으로 밝혀졌습니다. 예시된 것을 보려면 무한소 회전 SO(3)를 참조하십시오.

변환

우리는 어떤 차원, 즉 독립적인 평면, 순차적인 각도, 중첩된 차원에 적용되는 여러 분해의 존재를 보았습니다. 이 모든 경우에 우리는 행렬을 분해하거나 구성할 수 있습니다. 우리는 또한 3 × 3 회전 행렬에 특별한 주의를 기울였으며, 이것들은 양방향으로 더 많은 주의를 필요로 합니다(Stuelpnagel 1964).

쿼터니언

단위 쿼터니언 q = w + xi + yj + zk가 주어졌을 때, (열 벡터와 함께 사용되는) 등가의 사전 multip 라이딩 3 × 3 회전 행렬은

${\displaystyle Q={\begin{bmatrix}1-2y^{2}-2z^{2}&2xy-2zw&2xz+2yw\\2xy+2zw&1-2x^{2}-2z^{2}&2yz-2xw\\2xz-2yw&2yz+2xw&1-2x^{2}-2y^{2}\end{bmatrix}}.}$

이제 모든 쿼터니언 성분은 차수 2의 항에 2를 곱한 것으로 나타나며, 모든 항이 0이면 남은 것은 항등 행렬입니다. 따라서 단위 또는 비단위에 관계없이 모든 쿼터니언에서 3 × 3 회전 행렬로 효율적이고 강력한 변환이 가능합니다. 제공:

${\displaystyle {\begin{align}n&=w\times w+x\times x+y\times y+z\times z\\\s&={\begin{case}0&{\text{if}}n=0\{\frac {2}{n}&{\text{otherwise}}\end{case}}\\end{align}}}$

계산할 수 있습니다.

${\displaystyle Q={\begin{bmatrix}1-s(yy+zz)&s(xy-wz)&s(xz+wy)\\s(xy+wz)&1-s(xx+zz)&s(yz-wx)\\s(xz-wy)&s(yz+wx)&1-s(xx+yy)\end{bmatrix}}}$

단위 쿼터니언에 대한 요구에서 벗어나 0이 아닌 쿼터니언이 3 × 3 회전 행렬에 대한 균일한 좌표로 작용한다는 것을 발견했습니다. 앞에서 설명한 케일리 변환은 w 성분이 1이 되도록 쿼터니언을 스케일링함으로써 얻어집니다. 어떤 축을 중심으로 180° 회전하는 경우 w는 0이 되며, 이는 케일리 한계를 설명합니다.

주 대각선(추적)을 따라 있는 항목의 합과 1을 더한 값은 4 - 4(x²² + y² + z)이며, 이 값은 4w입니다². 따라서 우리는 트레이스 자체를 2w² + 2w² - 1로 쓸 수 있습니다. 그리고 이전 버전의 행렬에서 대각선 항목 자체가 2x² + 2w² - 1, 2y² + 2w² - 1, 2z² + 2w² - 1의 동일한 형태를 가지고 있음을 알 수 있습니다. 그래서 우리는 행렬 대각선을 사용하여 네 개의 쿼터니언 성분의 크기를 쉽게 비교할 수 있습니다. 실제로 합과 제곱근을 사용하여 네 가지 크기를 모두 얻을 수 있으며, 대각선 외 항목의 스큐 대칭 부분을 사용하여 일관된 부호를 선택할 수 있습니다.

${\displaystyle {\begin {align}t&=\operatorname {tr} Q=Q_{xx}+Q_{yy}+Q_{zz}\quad ({\text{the trace of }}Q)\\r&={\sqrt {1+t}}\\w&={\tfrac {1}{2}}r\\x&=\operatorname {sgn} \left(Q_{zy}-Q_{yz}\right)\left {\tfrac {1}{2}}{\sqrt {1+Q_{xx}-Q_{yy}-Q_{zz}}}\right \\y&=\operatorname {sgn} \left(Q_{xz}-Q_{zx}\right)\left {\tfrac {1}{2}}{\sqrt {1-Q_{xx}+Q_{yy}-Q_{zz}}}\right \\z&=\operatorname {sgn} \left(Q_{yx}-Q_{xy}\right)\left {\tfrac {1}{2}}{\sqrt {1-Q_{xx}-Q_{yy}+Q_{zz}}}\right \end{aligned}}}$

또는 한 제곱근과 나눗셈을 사용합니다.

${\displaystyle {\begin {align}t&=\operatorname {tr} Q=Q_{xx}+Q_{yy}+Q_{zz}\\r&={\sqrt {1+t}}\\s&={\tfrac {1}{2r}}\\w&={\tfrac {1}{2}}r\\x&=\left(Q_{zy}-Q_{yz}\right)s\\y&=\left(Q_{xz}-Q_{zx}\right)s\\z&=\left(Q_{yx}-Q_{xy}\right)s\end{aligned}}}$

트레이스 t가 음수가 아닌 한 수치적으로 안정적입니다. 그렇지 않으면 (거의) 0으로 나눌 위험이 있습니다. 이_xx 경우 Q가 가장 큰 대각선 엔트리이므로 x가 가장 큰 크기(다른 경우는 순환 순열에 의해 유도됨)를 갖는다고 가정하면 다음은 안전합니다.

${\displaystyle {\begin{aligned}r&={\sqrt {1+Q_{xx}-Q_{yy}-Q_{zz}}}\\s&={\tfrac {1}{2r}}\\w&=\left(Q_{zy}-Q_{yz}\right)s\\x&={\tfrac {1}{2}}r\\y&=\left(Q_{xy}+Q_{yx}\right)s\\z&=\left(Q_{zx}+Q_{xz}\right)s\end{aligned}}}$

누적된 수치 오차와 같이 행렬에 중대한 오차가 포함된 경우 대칭 4×4 행렬을 구성할 수 있습니다.

${\displaystyle K={\frac {1}{3}}{\begin{bmatrix}Q_{xx}-Q_{yy}-Q_{zz}&Q_{yx}+Q_{xy}&Q_{zx}+Q_{xz}&Q_{zy}-Q_{yz}\\Q_{yx}+Q_{xy}&Q_{yy}-Q_{xx}-Q_{zz}&Q_{zy}+Q_{yz}&Q_{xz}-Q_{zx}\\Q_{zx}+Q_{xz}&Q_{zy}+Q_{yz}&Q_{zz}-Q_{xx}-Q_{yy}&Q_{yx}-Q_{xy}\\Q_{zy}-Q_{yz}&Q_{xz}-Q_{zx}&Q_{yx}-Q_{xy}&Q_{xx}+Q_{yy}+Q_{zz}\end{bmatrix}},}$

그리고 가장 큰 크기의 고유 벡터 (x, y, z, w)를 찾습니다. (Q가 진정으로 회전 행렬이면 그 값은 1이 됩니다.) 이렇게 얻은 쿼터니언은 주어진 행렬에 가장 가까운 회전 행렬에 해당합니다(Bar-Itzhack 2000)(참고: 인용 기사의 공식화는 사후 곱셈이며 행 벡터와 함께 작동합니다).

극성 분해

n × n 행렬 M이 비특이적인 경우 열은 선형 독립 벡터이므로 그램-슈미트 프로세스는 이들을 정규 직교 기저로 조정할 수 있습니다. 수치 선형 대수학으로 표현하면, 우리는 QR 분해를 사용하여 M을 직교 행렬인 Q로 변환합니다. 그러나 우리는 종종 M에 가장 가까운 Q를 선호하는데, 이 방법은 이를 달성하지 못합니다. 이를 위해 우리가 원하는 도구는 극성 분해입니다(Fan & Hoffman 1955; Higham 1989).

근접성을 측정하기 위해 직교 변환에서 임의의 행렬 노름 불변량을 사용할 수 있습니다. 편리한 선택은 요소 차이의 제곱의 합인 프로베니우스 규범인 ‖ Q - M ‖ 제곱입니다. 이 글을 흔적으로 적으면, Tr, 우리의 목표는

QQ = I에 따라 Tr((Q - M)(Q - M))을 최소화하는 Q를 찾습니다.

행렬 용어로 작성되었지만 목적 함수는 단지 2차 다항식입니다. 우리는 도함수가 0인 곳을 찾음으로써 일반적인 방법으로 그것을 최소화할 수 있습니다. 3 × 3 행렬의 경우 직교 제약 조건은 Q의 항목이 만족해야 하는 6개의 스칼라 동등성을 의미합니다. 제약 조건을 통합하기 위해 대칭 행렬인 Y로 조립된 표준 기법인 라그랑주 승수를 사용할 수 있습니다. 따라서 우리의 방법은 다음과 같습니다.

(Q - M)(Q - M) + (QQ - I)Y)를 (Q의) Q에 대해 미분하고 0과 같습니다.

일반적으로, 우리는 방정식을 얻습니다.

${\displaystyle 0=2(Q-M)+2QY,}$

하도록

${\displaystyle M=Q(I+Y)=QS,}$

여기서 Q는 직교이고 S는 대칭입니다. 최소값을 보장하려면 Y 행렬(따라서 S)이 양의 명확해야 합니다. 선형대수학은 QS를 M의 극분해라고 부르고, S는 S = MM의 양의 제곱근입니다.

${\displaystyle S^{2}=\left(Q^{\mathsf {T}M\right)^{\mathsf {T}\left(Q^{\mathsf {T}M\right)=M^{\mathsf {T}}QQ^{\mathsf {T}}M=M^{\mathsf {T}}M}$

M이 비특이적인 경우 극성 분해의 Q 및 S 인자는 고유하게 결정됩니다. 그러나 S는 양의 확정이므로 S의 행렬식은 양수이므로 Q는 M의 행렬식의 부호를 상속합니다. 즉, Q는 회전 행렬이 아닌 직교만 보장됩니다. 이것은 피할 수 없는 일입니다. 음의 행렬식을 갖는 M에는 고유하게 정의된 가장 가까운 회전 행렬이 없습니다.

축과 각도

각도 θ와 단위 축 u로부터 회전 행렬 Q를 효율적으로 구성하기 위해, 우리는 엔트리 내의 대칭과 스큐 대칭을 이용할 수 있습니다. x, y, z가 축을 나타내는 단위 벡터의 성분이면,

${\displaystyle {\begin{aligned}c&=\cos \theta \\s&=\sin \\c&=1-c\end{aligned}}$

그리고나서

${\displaystyle Q(\theta )={\begin{bmatrix}xxC+c&xyC-zs&xzC+ys\\yxC+zs&yyC+c&yzC-xs\\zxC-ys&zyC+xs&zzC+c\end{bmatrix}}}$

쿼터니언을 결정하는 것과 같이 축과 각도를 결정하는 것은 부호까지만 가능합니다. 즉, (u, θ)와 (-u, -θ)는 q와 -q와 마찬가지로 동일한 회전 행렬에 해당합니다. 또한 축-각도 추출은 추가적인 어려움을 나타냅니다. 각도는 0°에서 180°로 제한할 수 있지만 각도는 형식적으로 360°의 배수로 모호합니다. 각도가 0이면 축이 정의되지 않습니다. 각도가 180°일 때 행렬이 대칭이 되므로 축을 추출하는 데 영향을 미칩니다. 180°의 배수 근처에서는 수치 문제를 피하기 위해 주의가 필요합니다. 각도를 추출할 때 θ와 동일한 atan2(sin θ, cos θ)를 갖는 2개의 인수 아크젠트는 아크코스의 둔감함을 피할 수 있으며, 단위 크기를 강제하기 위해 축 크기를 계산할 때 bruff-force 접근 방식은 언더플로우를 통해 정확도를 잃을 수 있습니다(Moler & Morrison 1983).

부분적인 접근은 다음과 같습니다.

${\displaystyle {\begin{aligned}x&=Q_{zy}-Q_{yz}\\y&=Q_{xz}-Q_{zx}\\z&=Q_{yx}-Q_{xy}\\r&={\sqrt {x^{2}+y^{2}+z^{2}}\\t&=Q_{xx}+Q_{yy}+Q_{zz}\\\theta &=\operatorname {atan2} (r,t-1)\end{aligned}}}$

축의 x-, y-, z- 성분은 r로 나뉩니다. 완전 강건한 접근법은 행렬 Q의 흔적인 t가 음수일 때 쿼터니언 추출과 마찬가지로 다른 알고리즘을 사용합니다. 각도가 0이기 때문에 r이 0일 때 행렬이 아닌 다른 소스에서 축을 제공해야 합니다.

오일러 각도

변환의 복잡성은 오일러 각도에 따라 증가합니다(여기서 넓은 의미로 사용됨). 첫 번째 어려움은 24개의 데카르트 축 순서 변형 중 어떤 것을 사용할 것인지를 정하는 것입니다. 세 각도가 θ, θ, θ라고 가정해보자; 물리학과 화학은 이것들을 다음과 같이 해석할 수 있습니다.

${\displaystyle Q(\theta _{1},\theta _{2},\theta _{3})=Q_{\mathbf {z} }(\theta _{1})Q_{\mathbf {y} }(\theta _{2})Q_{\mathbf {z} }(\theta _{3}),}$

항공기 역학이 사용할 수 있는 동안

${\displaystyle Q(\theta _{1},\theta _{2},\theta _{3})=Q_{\mathbf {z} }(\theta _{3})Q_{\mathbf {y} }(\theta _{2})Q_{\mathbf {x} }(\theta _{1}).}$

하나의 체계적인 접근법은 가장 오른쪽 축을 선택하는 것으로 시작됩니다. (x,y,z)의 모든 순열 중에서 축이 먼저 있는 곳은 두 곳뿐입니다. 하나는 짝수 순열이고 다른 하나는 홀수입니다. 따라서 패리티를 선택하면 중간 축이 설정됩니다. 그러면 맨 왼쪽 축에 첫 번째 축을 복제하거나 복제하지 않는 두 가지 선택 사항이 남게 됩니다. 이 세 가지 선택은 3 × 2 × 2 = 12가지 변형을 제공합니다. 정적 축 또는 회전 축을 선택하여 이를 24로 두 배로 늘립니다.

이는 각도에서 행렬을 구성하기에 충분하지만 여러 방식으로 다른 세 배는 동일한 회전 행렬을 제공할 수 있습니다. 예를 들어, 위의 zyz 규칙을 사용한다고 가정하면 다음과 같은 동등한 쌍이 있습니다.

(90°,	45°,	−105°)	≡	(−270°,	−315°,	255°)	360°의 배수
(72°,	0°,	0°)	≡	(40°,	0°,	32°)	단수 정렬
(45°,	60°,	−30°)	≡	(−135°,	−60°,	150°)	쌍안정적인 뒤집기

모든 주문에 대한 각도는 간결한 공통 루틴을 사용하여 찾을 수 있습니다(Herter & Lott 1993; Shomake 1994).

물리 짐벌 잠금의 수학적 유사체인 단수 정렬 문제는 중간 회전이 첫 번째 회전과 마지막 회전의 축을 정렬할 때 발생합니다. 90°의 짝수 배수 또는 홀수 배수로 모든 축 순서를 괴롭힙니다. 이러한 특이점은 회전 행렬의 특징이 아니며 오일러 각도를 사용할 경우에만 발생합니다.

회전 행렬을 각도가 아닌 직교 행 벡터(3D 응용 프로그램에서는 종종 오른쪽 벡터, 위쪽 벡터 및 바깥쪽 벡터로 명명됨)로 고려하고 조작할 때 특이점을 피할 수 있습니다. 쿼터니언과 작업할 때도 특이점을 피할 수 있습니다.

벡터 대 벡터 공식화

어떤 경우에는 벡터가 가장 짧은 경로(가장 작은 각도)를 통해 다른 벡터에 매핑되는 방법을 지정하여 회전을 설명하는 것이 흥미롭습니다. ${\displaystyle {\mathrm{}}^{}}$ ${\$에서 이는$$ 관련 회전 행렬을 완전히 설명합니다. 일반적으로, x, $y$∈ S ${\displaystyle \mathbb$ $\{$S}}가 주어졌을 때, 행렬

${\displaystyle R:=I+yx^{\mathsf {T}}-xy^{\mathsf {T}}+{\frac {1}{1+\langle x,y\rangle }}\left(yx^{\mathsf {T}}-xy^{\mathsf {T}}\right)^{2}}$

SO(n + 1)에 속하며 x를 y에 매핑합니다.^[20]

균일 랜덤 회전 행렬

우리는 때때로 균일하게 분포된 무작위 회전 행렬을 생성해야 합니다. 이것은 회전각이 0에서 2 π 사이에 균일하게 분포되어 있다는 것을 2차원으로 직관적으로 명확해 보입니다. 그 직관은 맞지만 더 높은 차원으로 이어지지는 않습니다. 예를 들어, 축-각 형태로 3 × 3 회전 행렬을 분해하는 경우 각도가 균일하게 분포되어서는 안 됩니다. 각도가 최대 θ에 있을 확률은 0 ≤ θ ≤ π의 경우 1/π(θ - sin θ)이어야 합니다.

SO(n)는 연결되고 국부적으로 콤팩트한 Lie 그룹이므로 임의의 회전(Lie 그룹 "번역")으로 구성될 때 분포가 변경되지 않는다는 균일성에 대한 간단한 표준 기준이 있습니다. 이 정의는 Haar measure라고 불리는 것에 해당합니다. León, Massé & Rivest(2006)는 케일리 변환을 사용하여 이 기준에 따라 행렬을 생성하고 테스트하는 방법을 보여줍니다.

또한 디아코니스 & 샤샤하니(1987)의 부분군 알고리즘을 사용하여 모든 차원에서 균일한 분포를 생성할 수 있습니다. 이는 다음과 같이 SO(n)의 중첩 차원 그룹 구조를 재귀적으로 이용합니다. 균일한 각도를 생성하고 2 × 2 회전 행렬을 구성합니다. n에서 n + 1로 이동하려면 n-sphere S에ⁿ 균일하게 분포된 벡터 v를 생성하고 n × n 행렬을 마지막 열(0, ..., 0, 1)로 다음으로 큰 크기로 포함한 다음 마지막 열이 v가 되도록 큰 행렬을 회전합니다.

여느 때와 마찬가지로 3×3 케이스에 대한 특별한 대안이 있습니다. 이러한 각 방법은 단위 간격에 균일하게 분포된 3개의 독립적인 무작위 스칼라로 시작됩니다. Arvo(1992)는 홀수 차원을 활용하여 가구주의 반사를 부정에 의한 회전으로 변경하고 이를 사용하여 균일한 평면 회전의 축을 조준합니다.

또 다른 방법은 단위 쿼터니언을 사용합니다. 회전 행렬의 곱셈은 쿼터니언의 곱셈과 동형이며, 단위 쿼터니언에 의한 곱셈은 단위 구를 회전시킵니다. 동형화는 국소 등각성이므로 SO(3)에서 균일한 분포를 생성하기 위해 S에서³ 균일한 분포를 사용할 수 있다고 즉시 결론지을 수 있습니다. 실제로: 각 요소가 정규 분포의 표본인 4요소 벡터를 만듭니다. 길이를 정규화하면 균일하게 샘플링된 랜덤 회전을 나타내는 균일하게 샘플링된 랜덤 단위 쿼터니언이 있습니다. 앞서 언급한 것은 차원 3의 회전에만 적용됩니다. 쿼터니언에 대한 일반화된 아이디어를 얻으려면 로터스를 살펴봐야 합니다.

오일러 각도도 사용할 수 있지만 각 각도가 균일하게 분포되어 있는 것은 아닙니다(Murnaghan 1962; Miles 1965).

축-각도 형태의 경우 축은 단위 방향 구 S에 대해 균일하게 분포되어 있는 반면, 각도는 앞서 언급한 [0, π]에 대해 불균일한 분포를 갖습니다(Miles 1965).

참고 항목

언급

메모들

참고문헌

• Arvo, James (1992), "Fast random rotation matrices", in David Kirk (ed.), Graphics Gems III, San Diego: Academic Press Professional, pp. 117–120, Bibcode:1992grge.book.....K, ISBN 978-0-12-409671-4
• Baker, Andrew (2003), Matrix Groups: An Introduction to Lie Group Theory, Springer, ISBN 978-1-85233-470-3
• Bar-Itzhack, Itzhack Y. (Nov–Dec 2000), "New method for extracting the quaternion from a rotation matrix", Journal of Guidance, Control and Dynamics, 23 (6): 1085–1087, Bibcode:2000JGCD...23.1085B, doi:10.2514/2.4654, ISSN 0731-5090
• Björck, Åke; Bowie, Clazett (June 1971), "An iterative algorithm for computing the best estimate of an orthogonal matrix", SIAM Journal on Numerical Analysis, 8 (2): 358–364, Bibcode:1971SJNA....8..358B, doi:10.1137/0708036, ISSN 0036-1429
• Cayley, Arthur (1846), "Sur quelques propriétés des déterminants gauches", Journal für die reine und angewandte Mathematik, 1846 (32): 119–123, doi:10.1515/crll.1846.32.119, ISSN 0075-4102, S2CID 199546746; reprinted as article 52 in Cayley, Arthur (1889), The collected mathematical papers of Arthur Cayley, vol. I (1841–1853), Cambridge University Press, pp. 332–336
• Diaconis, Persi; Shahshahani, Mehrdad (1987), "The subgroup algorithm for generating uniform random variables", Probability in the Engineering and Informational Sciences, 1: 15–32, doi:10.1017/S0269964800000255, ISSN 0269-9648, S2CID 122752374
• Engø, Kenth (June 2001), "On the BCH-formula in so(3)", BIT Numerical Mathematics, 41 (3): 629–632, doi:10.1023/A:1021979515229, ISSN 0006-3835, S2CID 126053191
• Fan, Ky; Hoffman, Alan J. (February 1955), "Some metric inequalities in the space of matrices", Proceedings of the American Mathematical Society, 6 (1): 111–116, doi:10.2307/2032662, ISSN 0002-9939, JSTOR 2032662
• Fulton, William; Harris, Joe (1991), Representation Theory: A First Course, Graduate Texts in Mathematics, vol. 129, New York, Berlin, Heidelberg: Springer, ISBN 978-0-387-97495-8, MR 1153249
• Goldstein, Herbert; Poole, Charles P.; Safko, John L. (2002), Classical Mechanics (third ed.), Addison Wesley, ISBN 978-0-201-65702-9
• Hall, Brian C. (2004), Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, Springer, ISBN 978-0-387-40122-5 (GTM 222)
• Herter, Thomas; Lott, Klaus (September–October 1993), "Algorithms for decomposing 3-D orthogonal matrices into primitive rotations", Computers & Graphics, 17 (5): 517–527, doi:10.1016/0097-8493(93)90003-R, ISSN 0097-8493
• Higham, Nicholas J. (October 1, 1989), "Matrix nearness problems and applications", in Gover, Michael J. C.; Barnett, Stephen (eds.), Applications of Matrix Theory, Oxford University Press, pp. 1–27, ISBN 978-0-19-853625-3
• León, Carlos A.; Massé, Jean-Claude; Rivest, Louis-Paul (February 2006), "A statistical model for random rotations", Journal of Multivariate Analysis, 97 (2): 412–430, doi:10.1016/j.jmva.2005.03.009, ISSN 0047-259X
• Miles, Roger E. (December 1965), "On random rotations in R³", Biometrika, 52 (3/4): 636–639, doi:10.2307/2333716, ISSN 0006-3444, JSTOR 2333716
• Moler, Cleve; Morrison, Donald (1983), "Replacing square roots by pythagorean sums", IBM Journal of Research and Development, 27 (6): 577–581, doi:10.1147/rd.276.0577, ISSN 0018-8646
• Murnaghan, Francis D. (1950), "The element of volume of the rotation group", Proceedings of the National Academy of Sciences, 36 (11): 670–672, Bibcode:1950PNAS...36..670M, doi:10.1073/pnas.36.11.670, ISSN 0027-8424, PMC 1063502, PMID 16589056
• Murnaghan, Francis D. (1962), The Unitary and Rotation Groups, Lectures on applied mathematics, Washington: Spartan Books
• Cayley, Arthur (1889), The collected mathematical papers of Arthur Cayley, vol. I (1841–1853), Cambridge University Press, pp. 332–336
• Paeth, Alan W. (1986), "A Fast Algorithm for General Raster Rotation" (PDF), Proceedings, Graphics Interface '86: 77–81
• Daubechies, Ingrid; Sweldens, Wim (1998), "Factoring wavelet transforms into lifting steps" (PDF), Journal of Fourier Analysis and Applications, 4 (3): 247–269, doi:10.1007/BF02476026, S2CID 195242970
• Pique, Michael E. (1990), "Rotation Tools", in Andrew S. Glassner (ed.), Graphics Gems, San Diego: Academic Press Professional, pp. 465–469, ISBN 978-0-12-286166-6
• Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007), "Section 21.5.2. Picking a Random Rotation Matrix", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8, archived from the original on 2011-08-11, retrieved 2011-08-18
• Shepperd, Stanley W. (May–June 1978), "Quaternion from rotation matrix", Journal of Guidance and Control, 1 (3): 223–224, doi:10.2514/3.55767b
• Shoemake, Ken (1994), "Euler angle conversion", in Paul Heckbert (ed.), Graphics Gems IV, San Diego: Academic Press Professional, pp. 222–229, ISBN 978-0-12-336155-4
• Stuelpnagel, John (October 1964), "On the parameterization of the three-dimensional rotation group", SIAM Review, 6 (4): 422–430, Bibcode:1964SIAMR...6..422S, doi:10.1137/1006093, ISSN 0036-1445, S2CID 13990266 (또한 NASA-CR-53568.)
• Varadarajan, Veeravalli S. (1984), Lie Groups, Lie Algebras, and Their Representation, Springer, ISBN 978-0-387-90969-1 (GTM 102)
• Wedderburn, Joseph H. M. (1934), Lectures on Matrices, AMS, ISBN 978-0-8218-3204-2

외부 링크

• "Rotation", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Mathworld에서의 회전 행렬
• 수학 인식의 달 2000 대화형 데모(Java 필요)
• 산술 페이지의 회전 행렬
• (이탈리아어로) 일반화된 오일러 각도에 의한 SOn(R)의 매개변수화
• 임의의 점에 대한 회전