전기적 임피던스
Electrical impedance| 기사 정보 |
| 전자기학 |
|---|
 |
전기공학에서 임피던스는 회로 [1]내 저항과 리액턴스의 결합 효과로 나타나는 교류에 대한 반대입니다.
양적으로 2단자회로소자의 임피던스는 그 단자간의 사인파전압의 복소표현과 그것을 [2]통과하는 전류의 복소표현의 비율이다.일반적으로 사인파 전압의 주파수에 따라 달라집니다.
임피던스는 교류(AC) 회로에 대한 저항 개념을 확장하여 규모만 있는 저항과 달리 크기와 위상을 모두 갖습니다.
임피던스는 저항과 동일한 단위를 갖는 복소수이며 SI 단위는 옴(Ω)입니다.그 기호는 보통 Z이며, 그 크기와 위상을 극의 Z δ δ z z z z its its its its its its its its its its its its its its its its단, 회로 분석의 목적으로는 데카르트 복소수 표현이 더 강력한 경우가 많습니다.
임피던스의 개념은 간단한 선형 법칙에 의해 사인파 전압과 전류를 관련지을 수 있기 때문에 전기 네트워크의 AC 분석을 수행하는 데 유용합니다.여러 포트 네트워크에서는 임피던스의 2단자 정의는 불충분하지만, 포트의 복잡한 전압과 이를 통과하는 전류는 임피던스 [3]매트릭스에 의해 여전히 선형적으로 관련되어 있습니다.
임피던스의 역수는 어드미턴스이며 SI 단위는 지멘스(이전에는 mho라고 불림)입니다.
전기적 임피던스를 측정하는 데 사용되는 기기를 임피던스 분석기라고 합니다.
서론
임피던스라는 용어는 1886년 [4][5]7월 올리버 헤비사이드에 의해 만들어졌다.Arthur Kennelly는 1893년에 [6]복소수 임피던스를 최초로 표현했다.
AC회로의 임피던스는 직류회로의 저항 외에 자기장에 의한 도체내 전압유도(유도)의 영향 및 도체간 전압에 의해 유도되는 전하의 정전저장(용량)을 포함한다.이 두 가지 효과에 의해 야기된 임피던스는 집합적으로 리액턴스라고 불리며 복합 임피던스의 가상 부분을 형성하는 반면 저항은 실제 부분을 형성합니다.
복소 임피던스

2 단자 회로 소자의 임피던스는 복소수 Z로 표시됩니다.극의 형태는 크기 및 위상 특성을 다음과 같이 편리하게 캡처합니다.
여기서 Z(\ Z는 전류 진폭에 대한 전압 차이 진폭의 비율을 나타내며, arg(Z ) { \)}(으로 기호 { \})는 전압과 전류j{ j 사이의 위상 차이를 나타냅니다.는 가상 단위이며,[7]: 21 전류 기호와의 혼동을 피하기 위해 이 문맥에서 ii 대신 됩니다.
데카르트 형식에서 임피던스는 다음과 같이 정의됩니다.
여기서 임피던스의 실제 부분은 R R이고, 가상 부분은 X(\X입니다.
임피던스를 더하거나 빼야 하는 경우에는 데카르트 형식이 더 편리합니다. 그러나 양을 곱하거나 나누면 극 형태를 사용하면 계산이 더 간단해집니다.병렬로 2개의 임피던스의 총 임피던스를 구하는 등의 회로 계산에서는 계산 중에 폼 간의 변환을 여러 번 요구할 수 있습니다.형식 간 변환은 복소수의 일반 변환 규칙을 따릅니다.
복잡한 전압과 전류
계산을 쉽게 하기 위해 사인파 전압 및 전류파는 일반적으로 V{\ V I {\ I[8][9]로 표시되는 복소수 시간 함수로 표현됩니다.
바이폴라 회로의 임피던스는 다음 양의 비율로 정의됩니다.
- I { = \_ { V} - \_ { } we 、 。
진폭 방정식은 전압 및 전류 진폭에 적용되는 익숙한 옴의 법칙이며, 두 번째 방정식은 위상 관계를 정의합니다.
복합 표현 타당성
복잡한 지수를 사용하는 이러한 표현은 (오일러의 공식에 의해) 다음과 같은 점에 주목함으로써 정당화될 수 있다.
전압 또는 전류 중 하나를 나타내는 실값 사인파 함수는 두 개의 복소수 함수로 나눌 수 있습니다.중첩 원리에 따라, 우리는 오른쪽의 두 복잡한 항의 거동을 분석함으로써 왼쪽의 정현동의 거동을 분석할 수 있다.대칭성을 고려할 때 오른쪽 항 하나만 분석하면 됩니다.결과는 다른 쪽과 동일합니다.어떤 계산의 마지막에, 우리는 더 나아가 다음을 주목함으로써 실값 사인파로 돌아갈 수 있다.
옴의 법칙
전기적 임피던스의 의미는 옴의 [10][11]법칙에 대입하여 이해할 수 있습니다.Z(\ Z를 가진 2단자 회로 소자가 위와 같이 사인파 전압 또는 전류에 의해 구동된다고 가정하면 다음과 같이 고정됩니다.
Z Z의 크기는 저항과 동일하게 작용하여 주어진 전류 I I Z(\ Z에 걸쳐 전압 진폭의 강하를 제공합니다.위상 계수를 통해 가 신호에 대해 arg (Z \Z)}의 위상만큼 지연됨을 알 수 있습니다(즉, 시간 영역에서 전류 신호는 전압 신호에 대해 δ 2 }{
임피던스가 옴의 법칙을 확장하여 AC회로를 커버하듯이, DC회로 분석의 다른 결과(전압분할, 전류분할, 테베닌의 정리, 노턴의 정리 등)도 저항을 임피던스로 대체함으로써 AC회로로 확장할 수 있습니다.
페이저스
위상수는 정현파 함수의 복잡한 진폭(크기와 위상)을 나타내는 일정한 복소수로 표현된다.위상자는 정현파[7]: 53 (AC 회로 등)와 관련된 계산을 단순화하기 위해 전기 공학자에 의해 사용되며, 여기서 종종 미분 방정식 문제를 대수적 문제로 줄일 수 있습니다.
회로 소자의 임피던스는 전압과 전류의 상대적 진폭과 위상에 의해 결정되는 소자를 통과하는 위상 전류에 대한 소자 전체의 위상 전압의 비율로 정의할 수 있습니다.이는 e t { et}}의 인수가 소거되는 것을 인식하여 위에 제시된 옴의 법칙의 정의와 동일합니다.
디바이스 예시
저항기
이상적인 저항의 임피던스는 순수하게 실재하며 저항 임피던스라고 불립니다.
이 경우 전압 및 전류 파형은 비례하며 위상이 일치합니다.
인덕터 및 콘덴서
이상적인 인덕터 및 캐패시터에는 순수하게 가상의 무효 임피던스가 있습니다.
주파수가 증가함에 따라 인덕터의 임피던스가 증가한다.
주파수가 증가함에 따라 콘덴서의 임피던스가 감소한다.
두 경우 모두 인가된 사인파 전압의 경우 결과 전류도 사인파이지만 직교에서는 전압과 90도의 위상이 어긋납니다.그러나 인덕터에서는 전류가 지연되고 캐패시터에서는 전류가 유도되는 등 위상이 반대되는 부호를 가집니다.
가상 단위 및 그 역수에 대해 다음 ID에 주의하십시오.
따라서 인덕터 및 캐패시터 임피던스 방정식을 극성 형태로 다시 작성할 수 있습니다.
진폭은 임피던스를 통해 주어진 전류 진폭에 대한 전압 진폭의 변화를 나타내며, 지수 계수는 위상 관계를 나타냅니다.
디바이스 고유의 임피던스 도출
다음은 저항, 콘덴서 및 인덕터의 3가지 기본 회로 요소 각각에 대한 임피던스의 도출입니다.아이디어는 임의의 신호의 전압과 전류 사이의 관계를 정의하도록 확장될 수 있지만, 이러한 파생은 사인파 신호를 가정합니다.푸리에 분석을 통해 사인파의 합으로 근사할 수 있기 때문에 이것은 임의의 주기 신호에 적용됩니다.
저항기
저항기의 경우, 다음과 같은 관계가 있습니다.
전압 신호를 고려하다
따라서
즉, AC 전압 진폭 대 저항 전체의 교류(AC) 진폭의 비율이 R{\ R이며 AC 전압이 저항을 가로질러 전류를 0도만큼 유도합니다.
이 결과는 일반적으로 다음과 같이 표현됩니다.
콘덴서
콘덴서의 경우 다음과 같은 관계가 있습니다.
전압 신호를 고려하다
따라서
따라서 이전과 같이
반대로 회로를 통과하는 전류가 정현파라고 가정할 경우, 그 복잡한 표현은 다음과 같습니다.
그리고 미분 방정식을 적분한다.
로 이어지다
Const 항은 AC 사인파 전위에 중첩된 고정 전위편향을 나타내며, AC 분석에는 아무런 역할을 하지 않는다.이 목적을 위해 이 항은 0으로 가정할 수 있으며, 따라서 다시 임피던스는
인덕터
인덕터의 경우 (패러데이의 법칙에서) 다음과 같은 관계가 있습니다.
현재 신호는 다음과 같습니다.
다음과 같습니다.
이 결과는 일반적으로 극의 형태로 다음과 같이 표현된다.
또는, 오일러의 공식을 사용하여,
콘덴서의 경우와 마찬가지로 전압과 전류의 복잡한 표현으로부터 직접 또는 인덕터의 두 극 사이에 정현파 전압을 가정함으로써 이 공식을 도출할 수도 있다.후자의 경우 위의 미분방정식을 적분하면 인덕터를 통과하는 고정 DC 바이어스를 나타내는 전류의 항이 일정해집니다.주파수 영역 임피던스를 사용한 AC 분석에서는 한 번에 하나의 주파수가 고려되고 DC는 이 컨텍스트에서 별도의 주파수인 0Hz를 나타내기 때문에 이 값은 0으로 설정됩니다.
일반화 s면 임피던스
jµ로 정의되는 임피던스는 정상상태 AC신호에 의해 구동되는 회로에만 엄격하게 적용할 수 있습니다.임피던스의 개념은 jµ 대신 복잡한 주파수를 사용함으로써 임의의 신호로 통전되는 회로로 확장할 수 있습니다.복소 주파수는 기호 s로 주어지며 일반적으로 복소수이다.신호는 신호의 시간영역 표현의 라플라스 변환을 취함으로써 복잡한 주파수로 표현된다.이 일반적인 표기법에서의 기본 회로 소자의 임피던스는 다음과 같습니다.
| 요소 | 임피던스식 |
|---|---|
| 저항기 | |
| 인덕터 | |
| 콘덴서 |
DC 회로의 경우 s = 0으로 단순화됩니다.정상 상태의 정현파 AC 신호 s = j140.
형식 파생
전기 부품의 Z(\ Z는 전압의 Laplace 변환과 전압의 전류 사이의 비율로 정의됩니다.
서 s + {\ { s = \+ j \ }는 복잡한 Laplace 파라미터입니다.예를 들어 콘덴서의 I-V 법칙에 따르면 { (t )} { v () / L { ( ) { style \ { } \ { ( t ) \ } = { L } \ { L } \ { 를 클릭합니다.
체계(모든 신호가 수학적으로 단순한 복소수 v ^ j t { v(t) = i ( ) ^ = = e ^ = i) v} ) 임피던스는 전압 대 전류 비율로 간단히 계산할 수 있으며, 여기서 공통 시간 종속 계수는 다음과 같이 상쇄됩니다.
캐패시터의 i( ) () / t v () \ i ( t )( t ) / \ { } t \ C , () / C( t 。위상 도메인은 Laplace 파라미터의 [12]치수 중 하나가 부족하지만 주파수 도메인으로 불리기도 합니다.정상상태 AC의 경우 복합임피던스의 극형식은 전압과 전류의 진폭과 위상을 관련짓습니다.특히:
- 복합 임피던스의 크기는 전류 진폭에 대한 전압 진폭의 비율입니다.
- 복합 임피던스의 위상은 전류가 전압을 지연시키는 위상 이동입니다.
이들 2개의 관계는 실제 회로에서 실제로 측정하는 신호의 일부인 복잡한 지수(단계 참조)의 실제 부분을 취한 후에도 유지됩니다.
저항 대 리액턴스
저항과 리액턴스는 함께 다음 관계를 통해 임피던스의 크기와 위상을 결정합니다.
많은 애플리케이션에서 전압과 전류의 상대 위상은 중요하지 않으므로 임피던스의 크기만 중요합니다.
저항
R R은 임피던스의 실제 부분입니다. 순수 저항 임피던스를 가진 장치는 전압과 전류 사이에 위상 편이를 보이지 않습니다.
리액턴스
X({X})는 임피던스의 가상 부분이며, 리액턴스가 유한한 컴포넌트는 임피던스 전압과 임피던스를 통과하는 전류 사이에서 위상 편이({를 유도합니다.
순수 반응성 성분은 구성부품을 통과하는 사인파 전류와 직교하는 구성부품에 걸친 사인파 전압으로 구별된다.이는 구성 요소가 회로로부터 에너지를 번갈아 흡수하고 나서 회로로 에너지를 돌려보낸다는 것을 의미합니다.순수한 리액턴스는 전력을 소모하지 않습니다.
용량 리액턴스
콘덴서는 신호 주파수에 반비례하는 순수 반응 임피던스를 가집니다.콘덴서는 절연체로 분리된 두 개의 도체로 구성되어 있으며, 유전체라고도 합니다.
마이너스 부호는 임피던스의 가상 부분이 음임을 나타냅니다.
저주파에서는 콘덴서가 개방 회로에 접근하기 때문에 전류가 흐르지 않습니다.
콘덴서에 인가되는 DC 전압은 한쪽에 전하가 누적됩니다. 누적된 전하에 의한 전계가 전류에 대한 역행의 원천입니다.충전과 관련된 전위가 인가된 전압의 균형을 정확히 맞추면 전류가 0이 됩니다.
AC 전원으로 구동되는 콘덴서는 전위차 부호가 변화하고 전하가 소멸되기 전에 제한된 전하만 축적합니다.주파수가 높을수록 축적되는 전하가 적어지고 전류에 대한 저항도 작아집니다.
유도 리액턴스
유도 L은 신호 f(\ f 및 L(\ L에 비례합니다.
인덕터는 코일 도체로 구성됩니다.패러데이의 전자 유도 법칙은 전류 루프를 통한 자속 B B의 변화율에 따라 E전압 대향 전류)를 제공합니다.
N N 루프가 코일로 구성된 인덕터의 경우 다음과 같습니다.
back-emf는 전류 흐름을 방해하는 원인입니다.정전류는 변화율이 0이며, 인덕터를 단락으로 간주합니다(일반적으로 저항률이 낮은 재료로 만들어집니다).교류는 주파수에 비례하는 시간 평균 변화율을 가지며, 이는 주파수에 따른 유도 리액턴스의 증가를 일으킵니다.
총 리액턴스
총 리액턴스는 다음과 같습니다.
- L + {X_ (X 는 음수입니다)
총 임피던스가
임피던스의 조합
다수의 단순한 컴포넌트 네트워크의 총 임피던스는 임피던스를 직렬 및 병렬로 조합하는 규칙을 사용하여 계산할 수 있습니다.이 규칙은 일반적으로 복소수라는 점을 제외하고 저항을 결합하는 규칙과 동일합니다.그러나 일반적인 경우에서는 직렬 및 병렬 외에 동등한 임피던스 변환이 필요합니다.
시리즈의 조합
직렬로 연결된 구성 요소의 경우 각 회로 요소를 통과하는 전류는 동일합니다. 총 임피던스는 구성 요소 임피던스의 합입니다.
또는 명시적으로 실제 및 가상의 용어로:
병렬 조합
병렬로 연결된 구성 요소의 경우 각 회로 소자의 전압은 동일합니다. 두 요소를 통과하는 전류의 비율은 임피던스의 역비입니다.
따라서 역 총 임피던스는 컴포넌트 임피던스의 역합입니다.
또는 n = 2인 경우:
등가 Z 는 등가 직렬 R 및 X [13]로 계산할 수 있습니다.
측정.
디바이스와 전송로의 임피던스 측정은 무선 테크놀로지 및 기타 분야에서 실질적인 문제입니다.임피던스 측정은 1개의 주파수로 실행할 수도 있고, 특정 주파수 범위에 걸친 디바이스 임피던스의 변동에 관심이 있을 수도 있습니다.임피던스를 옴 단위로 직접 측정 또는 표시하거나 임피던스와 관련된 다른 값을 표시할 수 있습니다.예를 들어, 무선 안테나에서는 정재파 비 또는 반사 계수가 임피던스만 표시하는 것보다 더 유용할 수 있습니다.임피던스를 측정하려면 전압과 전류의 크기와 그 사이의 위상차를 측정해야 합니다.임피던스는 종종 직류 휘트스톤 브리지와 유사한 "브릿지" 방식으로 측정됩니다. 교정된 기준 임피던스는 테스트 대상 장치의 임피던스 효과를 상쇄하도록 조정됩니다.전원 전자 장치의 임피던스 측정은 작동 장치에 전원을 공급하고 동시에 측정해야 할 수 있습니다.
장치의 임피던스는 전압과 전류의 복잡한 분할로 계산할 수 있습니다.장치의 임피던스는 저항기와 직렬로 장치에 사인파 전압을 인가하고 저항기와 장치 간에 전압을 측정하여 계산할 수 있습니다.적용된 신호의 주파수를 스위프하여 이 측정을 수행하면 임피던스 위상 및 [14]크기가 제공됩니다.
임펄스 응답을 고속 푸리에 변환(FFT)과 조합해 사용하면 다양한 전기 [14]장치의 전기적 임피던스를 신속하게 측정할 수 있습니다.
LCR 미터(인덕턴스(L), 캐패시턴스(C) 및 저항(R))은 구성 요소의 인덕턴스, 저항 및 캐패시턴스를 측정하는 데 일반적으로 사용되는 장치입니다. 이러한 값을 통해 모든 주파수의 임피던스를 계산할 수 있습니다.
예
LC 탱크 회로를 검토합니다.회로의 복잡한 임피던스는
에서 textstyle 1 Z의 이 최소(이 경우 실제로 0과 동일)임을 알 수 있습니다.
따라서 기본 공명 각 주파수는
가변 임피던스
일반적으로 임피던스도 어드미턴스도 시간에 따라 변화할 수 없습니다.이는 임피던스도 t < +'의 복잡한 지수에 대해 정의되기 때문입니다.복잡한 지수전압 대 전류비가 시간 또는 진폭에 따라 변화할 경우 회로소자는 주파수 영역을 사용하여 설명할 수 없습니다.그러나, 많은 구성 요소와 시스템 (예를 들어, 무선 튜너에 사용되는 정맥류)은 작은 신호와 작은 관측 윈도우에 대해 선형 시간 불변(LTI)인 것처럼 보이는 비선형 또는 시간 변동 전류 비율을 보일 수 있습니다. 따라서, 대략적으로 시간 변동 임피던스를 가진 것으로 설명할 수 있습니다.다음 설명은 대략적인 것입니다.큰 신호 변동 또는 넓은 관찰 창에서 전류 관계에 대한 전압은 LTI가 아니며 임피던스로 설명할 수 없습니다.
「 」를 참조해 주세요.
- 생체전기 임피던스 분석
- 특성 임피던스 – 전기공학 개념
- 동적 확성기의 전기적 특성
- 고임피던스
- 임피턴스
- 임피던스 분석기
- 임피던스 브리징
- 임피던스 심전도
- 임피던스 제어
- 임피던스 매칭– 전자기기 실습
- 임피던스 미생물학
- 부 임피던스 컨버터 – 회로에 에너지를 주입하는 능동 회로
- 저항 거리 – 노드 간 전기 저항 메트릭
- 전송선 임피던스 – 신호 현상
- 범용 유전 반응
메모들
- ^ jj})는 전기 공학에서 사용되는 가상의 단위입니다. , j- ({ j{-입니다.현재 많이 사용되고 있기 때문에 사용되지 않습니다.
레퍼런스
- ^ Slurzberg; Osterheld(1950).라디오와 TV를 위한 전기의 필수 요소.제2판맥그로힐 360-362페이지
- ^ 칼레가로, L. (2012년)전기 임피던스: 원리, 측정 및 응용 프로그램.CRC 프레스, 페이지 5
- ^ 칼레가로 1.6장
- ^ 과학, 1888년 페이지 18
- ^ 올리버 헤비사이드, The Electrician, 1886년 7월 23일자, Oliver Heaviside는 전기 논문, 제2권, 제64쪽, AMS 서점으로 전재되었다. ISBN0-8218-3465-7
- ^ 케넬리, 아서임피던스(AIEE, 1893)
- ^ a b Gross, Charles A. (2012). Fundamentals of electrical engineering. Thaddeus Adam Roppel. Boca Raton, FL: CRC Press. ISBN 978-1-4398-9807-9. OCLC 863646311.
- ^ 복잡한 임피던스, 하이퍼 물리
- ^ Horowitz, Paul; Hill, Winfield (1989). "1". The Art of Electronics. Cambridge University Press. pp. 31–32. ISBN 978-0-521-37095-0.
- ^ AC 옴의 법칙, 하이퍼 물리
- ^ Horowitz, Paul; Hill, Winfield (1989). "1". The Art of Electronics. Cambridge University Press. pp. 32–33. ISBN 978-0-521-37095-0.
- ^ Alexander, Charles; Sadiku, Matthew (2006). Fundamentals of Electric Circuits (3, revised ed.). McGraw-Hill. pp. 387–389. ISBN 978-0-07-330115-0.
- ^ 병렬 임피던스 식, 하이퍼 물리
- ^ a b George Lewis Jr.; George K. Lewis Sr. & William Olbricht (August 2008). "Cost-effective broad-band electrical impedance spectroscopy measurement circuit and signal analysis for piezo-materials and ultrasound transducers". Measurement Science and Technology. 19 (10): 105102. Bibcode:2008MeScT..19j5102L. doi:10.1088/0957-0233/19/10/105102. PMC 2600501. PMID 19081773.
외부 링크
- ECE 209: LTI 시스템으로서의 회선 리뷰– Laplace-domain 회로 해석의 간단한 설명.임피던스의 정의가 포함되어 있습니다.


 전류 진폭에 대한 전압 차이 진폭의 비율을 나타내며,
전류 진폭에 대한 전압 차이 진폭의 비율을 나타내며, 



 ,
, 







![\ \cos(\omega t+\phi )={\frac {1}{2}}{\Big [}e^{j(\omega t+\phi )}+e^{-j(\omega t+\phi )}{\Big ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac6d2d678fbcb897277792546ef55f422d17c2dc)




 위상만큼 지연됨을 알 수 있습니다(즉, 시간
위상만큼 지연됨을 알 수 있습니다(즉, 시간  인수가 소거되는 것을 인식하여 위에 제시된
인수가 소거되는 것을 인식하여 위에 제시된




































 신호
신호 


 변화율에 따라
변화율에 따라 




 음수입니다)
음수입니다)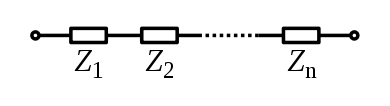






 등가 직렬
등가 직렬 







 .
.

