만델브로세트

만델브로 집합(/ˈmændlbroʊt, -brɒt/)은 비교적 간단한 정의를 가진 2차원 집합으로, 특히 확대됨에 따라 큰 복잡성을 보입니다.그것은 미적인 매력과 프랙탈 구조로 인기가 많습니다.집합은 복소 평면에서 함수 ${\displaystyle f_{}c}$ (${\displaystyle }$z ) = ${\displaystyle {}^{}}$ ${\displaystyle 2^{}}$+ ${\displaystyle c}${\$displaystyle f_{c}(z$) = $z^{2}$ + $c}$가 z = ${\displaystyle 0}${\$displaystyle$ z=$0$에서 $시작$할 때 무한대로 발산되지 않는 $복소수$ c$${\$displaystyle$ c$}$로 정의됩니다. 즉, ${\displaystyle {수열}_{}}$ f${\displaystyle {}_{}}$c (${\displaystyle 0)}${\$displaystyle f_{c}(0$ ${\displaystyle f_{}}$c (${\displaystyle 0)}$ ${\displaystyle f_{c}(f$)$_{c}(0$ 등은 절대값으로 경계를 유지합니다.

이 세트는 1978년 로버트 W. 브룩스와 피터 마텔스키에 의해 클라이니아 그룹에 ^[3]대한 연구의 일부로 처음 정의되고 그려졌습니다.그 후 1980년, Benoit Mandelbrot는 뉴욕 요크타운 하이츠에 있는 IBM의 토마스 J. 왓슨 연구 센터에서 일하면서 세트의 고품질 시각화를 얻었습니다.

만델브로 집합의 이미지는 확대에서 점진적으로 더 미세한 재귀적 세부 사항을 나타내는 무한 복잡한 경계를 보여줍니다. 수학적으로 만델브로 집합의 경계는 프랙탈 곡선입니다.이 재귀적 세부사항의 "스타일"은 검사하는 설정된 경계의 영역에 따라 달라집니다.만델브로 집합 이미지는 복소수를 샘플링하고 각 $샘플점{\displaystyle }$ c$${\$displaystyle$ c$\}$에 대해 $시퀀스{\displaystyle {}_{}}$ ${\displaystyle f_{}}$c (${\displaystyle 0}$ ${\displaystyle ),}$ ${\displaystyle {}_{}{c}_{}}$ ( ${\displaystyle f_{}}$c (${\displaystyle 0),}$ … ${\displaystyle f_{c}(0)), f_{c}(f_{c}(0)),\dotsc }$가 무한대로 이동하는지 테스트하여 생성할 수 있습니다.c$${\$displaystyle$ c$}$의 실수 부분과 허수 ${\displaystyle 부분}$을 복소 평면의 이미지 좌표로 처리하면,${\displaystyle {}_{}\mathrm{수열}}$f${\displaystyle }$c ( ${\displaystyle 0_{}}$), ${\displaystyle {}_{}{c}_{}}$ (${\displaystyle \mathrm{f}}$c${\displaystyle }$( 0 $),$ ... {\$displaystyle$f_{$c}(0), f_{c}(f_{c}(0$)),\dotsc$$ $}$가 임의로 선택한 임계값과 교차합니다(-2가 복소이므로 임계값은 2 이상이어야 함).집합 내에서 크기가 가장 크지만 그렇지 않은 경우 임계값이 임의입니다.c$${\$displaystyle$ c$}$을(를) 일정하게 유지하고 z$${\$displaystyle$ z$}$의 초기 값을 대신 $변경$하면 점$c{\displaystyle }$ {\$displaystyle$ c$$$}$에 해당하는 줄리아 세트를 얻습니다.

만델브로 집합은 미적인 매력과 간단한 규칙의 적용으로부터 발생하는 복잡한 구조의 예로서 수학 외부에서 인기를 끌게 되었습니다.그것은 수학적 시각화, 수학적 아름다움, 모티브의 가장 잘 알려진 예 중 하나입니다.

역사

만델브로 집합은 20세기 초 프랑스 수학자 피에르 파투와 가스통 줄리아에 의해 처음 조사된 분야인 복잡한 역학에 기원을 두고 있습니다.프랙탈은 1978년 로버트 W. 브룩스와 피터 마텔스키에 의해 클라이니아 ^[3]그룹 연구의 일부로 처음 정의되고 그려졌습니다.1980년 3월 1일, 뉴욕 요크타운 하이츠에 위치한 IBM의 토마스 J. 왓슨 연구 센터에서 베누아 만델브로(Benoit Mandelbrot)가 처음으로 ^[4]세트를 시각화했습니다.

만델브로는 ^[5]1980년에 등장한 논문에서 이차 다항식의 매개변수 공간을 연구했습니다.만델브로 집합에 대한 수학적 연구는 실제로 수학자 Adrien Douady와 John H. Hubbard (1985)^[6]의 연구로부터 시작되었는데, 그는 프랙탈 기하학에서의 영향력 있는 업적으로 만델브로를 기리기 위해 그 집합의 많은 기본적인 성질들을 확립하고 그 집합의 이름을 지었습니다.

수학자 하인츠 오토 페이트겐과 피터 리히터는 사진, 책 그리고 독일 ^[7]괴테 인스티튜트의 국제 순회 전시회 (1985)^[8][9]로 세트를 홍보한 것으로 유명해졌습니다.

1985년 8월 사이언티픽 아메리칸의 표지 기사는 만델브로 집합을 계산하는 알고리즘을 소개했습니다.표지는 브레멘 ^[10]대학의 Peitgen, Richter, Saupe가 만들었습니다.만델브로 세트는 1980년대 중반에 컴퓨터 그래픽 데모로 유명해졌는데, 이때 개인용 컴퓨터는 그 세트를 ^[11]고해상도로 플롯하고 전시할 수 있을 정도로 강력해졌습니다.

Douady와 Hubbard의 연구는 복잡한 역학과 추상 수학에 ^[12]대한 관심이 증가하는 동안 발생했고, 그 ^{[citation needed]}이후로 만델브로 집합에 대한 연구는 이 분야의 중심이었습니다.

형식적 정의

만델브로 집합은 2차 지도의 반복 하에서 $임계점$ z = $0$ {\$textstyle$ z =$0}$의 궤도를 갖는 복소 평면의 c 값들의 집합입니다.

${\displaystyle z_{n+1}=z_{n}^{2}+c}$

한정된 ^[13]채로 있습니다.따라서 복소수 c는 z ${\displaystyle 0_{}}$ = ${\displaystyle 0}$ {\$displaystyle z_{0$}=$0}$으로 $시작$하여 반복 적용을 반복할 때 ${\displaystyle z_{}}$ n$${\$displaystyle z_{n}}$의 절대값이 n > {\$displaystyle$ n$>0$에 대해 경계를 유지하는 경우 만델브로 집합의 멤버입니다.

예를 들어 c = 1의 경우 수열은 0, 1, 2, 5, 26, ...이며 무한대의 경향이 있으므로 1은 만델브로 집합의 요소가 아닙니다.반면 c = - ${\displaystyle 1}${\$displaystyle$ c=-$1$의 경우 시퀀스가 0, -1, 0, -1, 0, ...이며 이는 유계이므로 -1은 집합에 속합니다.

만델브로 집합은 또한 2차 $다항식{\displaystyle }$f ( z) = z 2 +${\displaystyle c^{}}${\$displaystyle$ f$(z$ = $z^{2}$ +$c$의 연결 궤적으로 정의될 수 있으며, 매개 $변수$의 공간 c {\$displaystyle$ c$}$의 부분 집합이며, 이 부분 집합은 해당 다항식의 줄리아 집합이 연결된 집합을 형성합니다$.$같은 방식으로, 만델브로 집합의 경계는 다항식의 동적 거동이 (반복 반복될 때) ^{[citation needed]}급격하게 변하는 근처의 매개 변수의 부분 집합인 이 이차 패밀리의 분기 궤적으로 정의될 수 있습니다.

기본속성

만델브로 집합은 원점을 중심으로 반지름 2의 닫힌 디스크에 포함되어 있고 닫혀 있기 때문에 콤팩트한 집합입니다.점 $c{\displaystyle }${\$displaystyle$ c$}$는 ${\displaystyle \mathrm{모든}}$ $n{\displaystyle }$ 0 {\$displaystyle$ n$\backslash$$geq$ 0}에 대해 ${\displaystyle z_{}}$ n ${\displaystyle \le {}_{}}$ ${\displaystyle 2}${\$displaystyle z_{n}$ \$leq$ 2$}$인 경우에만 만델브로 집합에 속합니다. 즉$,$ ${\displaystyle c_{}}$ {\$displaystyle$ c$}$가 M ${\displaystyle$ M$\}$이고$,$ 해당 절대값이 초과하는 경우에는 z n$${\$displaystyle z_{n}$의 절대값이 2 이하로 유지되어야 합니다.s 2, 순서가 무한대로 빠져나갑니다.c = ${\displaystyle z_{}}$ 1$${\$displaystyle$ c =$z_{$1$\}\}$이므로, $≤$ 2 {\$displaystyle c$ \$leq$ 2$\}$을(를) $따르므로$, c {\$displaystyle$c$}$는 원점을 중심으로 항상 반경 2의 닫힌 디스크에 있게 $됩니다$.

M ${\displaystyle$ M$}$과(와) 실제 축의 교점은 구간${\displaystyle [-2,}$ ${\displaystyle \frac{14}{}]}$ ${\displaystyle [-2,{\frac {1}{4}}}$입니다$.$이 구간에 따른 매개변수는 실제 로지스틱 패밀리의 매개변수와 일대일 대응 관계에 놓일 수 있습니다.

${\displaystyle x_{n+1}=module_{n}(1-x_{n}),\module r\in [1,4]입니다.}$

서신은 다음과 같이 전달됩니다.

${\displaystyle z=r\left({\frac {1}{2}-x\right)),\lot c={\frac {r}{2}}\left(1-{\frac {r}{2}\right).}$

이것은 로지스틱 패밀리의 전체 매개 변수 공간과 만델브로 ^{[citation needed]}집합의 매개 변수 공간 사이의 대응 관계를 제공합니다.

Douady와 Hubbard는 만델브로 세트가 연결되어 있음을 보여주었습니다.그들은 만델브로 집합의 상보와 닫힌 단위 디스크의 상보 사이의 명시적인 등각 동형을 구성했습니다.만델브로는 원래 만델브로 집합이 단절되어 있다고 추측했습니다.이 추측은 M ${\displaystyle$ M$\}$의 $서로{\displaystyle }$ 다른 부분을 연결하는 얇은 필라멘트를 감지할 수 없는 프로그램에 의해 생성된 컴퓨터 사진에 기초했습니다. 추가 실험 후, 그는 M ${\displaystyle$ M$}$이(가) 연결되어야 한다고 $결정$하면서 추측을 수정했습니다.2001년 ^[14]Jeremy Kahn에 의해 연관성에 대한 위상학적 증거가 발견되었습니다.

M ${\displaystyle$ M$\}$의 연결성에 대한 Douady와 Hubbard의 증명에서 발생하는 만델브로 세트의 보완을 균일화하기 위한 동적 공식은 만델브로 세트의 외부 광선을 발생시킵니다.이 광선들은 조합적인 용어로 만델브로 집합을 연구하고 요코즈 파라퍼즐의 ^[15]뼈대를 형성하는 데 사용될 수 있습니다.

만델브로 집합의 경계는 이차 다항식 계열의 분기점입니다.즉, Mandelbrot 집합의 경계는 ${\displaystyle {2차}_{}}$ ${\displaystyle {\mathrm{맵}}_{}^{}{}_{}{}_{}^{}}$ ${\displaystyle n_{}^{}}$= z${\displaystyle {}_{}^{}}$ -$$ + c {\$displaystyle$ z_${n$}= $z_{n-1$}^{2$}+c}$의 역학이 c${\displaystyle ,}${\$displaystyle$c에 민감한 의존성을 나타내는 모든 $매개$ 변수 c$${\$displaystyle$ c$}$의 집합입니다. 즉${\displaystyle ,}$ c의 $임의$의 작은 변화 하에서 갑자기 변경됩니다$.$ {\$displaystyle$ c$.}$ 이는 co일 수 있습니다.n은 다항식 렘니케이트로 알려진 일반적인 유형의 평면 대수 곡선, 만델브로 곡선의 순서의 극한 집합으로 구성됩니다.만델브로 곡선은 ${\displaystyle p_{}}$ 0 =${\displaystyle z}$, ${\displaystyle \text{p}{n}_{}}$ + ${\displaystyle 1_{}}$ = ${\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}}$ 2${\displaystyle {}_{}^{}}$+ ${\displaystyle z}${\$displaystyle p_{0$}= $z,\ p_{n+1$}= $p_{n}^{2}+z$를 $설정$한 다음 복소 평면에 ${\displaystyle 있는}$ 점 ${\displaystyle p_{}}$n ( ${\displaystyle z)}$ = ${\displaystyle 2}${\$displaystyle p_{n}(z)$ = $2}$를 x 및 y의 $실제$ 데카르트 평면의 2도 n${\displaystyle {}^{}}$+ ${\displaystyle 1^{}}${\$displaystyle$ 2$^{n+1}$의 곡선으로 해석하여 정의됩니다.각 n > ${\displaystyle$n > $0}$은 ${\displaystyle {pn}_{}}$ ${\$ $아래$의 반지름 2의 초기 원의 매핑입니다.이러한 대수적 곡선은 아래에 언급된 "탈출 시간 알고리즘"을 사용하여 계산된 만델브로 집합의 이미지에 나타납니다.

기타속성

주요 심장 박동 및 주기 전구

이 절에서는 출처를 언급하지 않습니다. 신뢰할 수 있는 자료에 인용문을 추가하여 이 부분을 개선하는 데 도움을 주시기 바랍니다. 출처가 밝혀지지 않은 자료에 이의를 제기하여 제거할 수 있습니다.(2023년 7월) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

주요 심장 박동수는 1기 대륙입니다.맵이 적용되는 $매개{\displaystyle }$ 변수 c ${\displaystyle$ c$}$의 영역입니다.

${\displaystyle f_{c}(z)=z^{2}+c}$

매력적인 고정점을 가지고 있습니다.양식의 모든 매개 변수로 구성됩니다.

${\displaystyle c(\mu ):={\frac {\mu}{2}}\left(1-{\frac {\mu}{2}}\right)}$

열려 있는 단위 디스크의 $일부{\displaystyle }$μ {\$displaystyle \mu}$에 대해.

주 심장 박동의 왼쪽에는 c = - 3${\displaystyle /4}$ $지점$ ${\displaystyle$ c = - $3/4$원형 전구)에 부착된 주기-2 전구가 보입니다.전구는$$${\displaystyle {fc}_{}}${\$displaystyle$ c$}$로 $구성$되어 $있으며{\displaystyle {}_{}}$, fc {\$displaystyle f_{c}$는 주기 2의 매력적인 주기를 가집니다.이것은 -1을 중심으로 한 반지름 1/4의 채워진 원입니다.

더 일반적으로, 모든 양의 ${\displaystyle >}$ 2{\$displaystyle$$$q > $2$에 대하여, 주기-q 구근이라고 불리는 주요 심장율동체에 접하는${\displaystyle }$ϕ$$(${\displaystyle \mathrm{여기}}$서 ϕ$${\$displaystyle \phi }$는 오일러 phi 함수를 나타냄) 원형 구근이 존재하며, $이$는 ${\displaystyle {fc}_{}}${\$displaystyle f_{c}$가 매력적인 순환을 갖는 $매개변수$ c$${\$displaystyle$ c$}$로 구성됩니다.$q$ ${\displaystyle q$ 구간의 e. 보다 구체적으로, $q$ ${\displaystyle$ q$}$번째 단합 r =$$ ${\displaystyle 2^{}}$ π i ${\displaystyle {\frac{q}{}}^{}}$ ${\displaystyle$ r = $e^{2\pi$ i${\frac {p}{q}}}}}($서, 0< q< ${\displaystyle$ 0$<\frac {p}}}}),$ $p$ {\$displaystyle {p}{q}}$ 전구라고 하는 하나의 구간-q 전구가 있습니다.파라미터에서 주 심장율동체와 접하게 됩니다.

${\displaystyle c_{\frac {p}{q}}:=c(r)={\frac {r}{2}}\left(1-{\frac {r}{2}\right),}$

그리고$$q {\$displaystyle$q} - 조합 ${\displaystyle \frac{\mathrm{회전수}}{}}$ p$$q ${\displaystyle {p}{$q$\}\}$인 $사이클{\displaystyle }$ 매개 변수를 포함합니다. 더 정확하게 말하면, 흡인 사이클을 포함하는$$q {\$displaystyle$q$$}개의 주기적인 Fatou 구성 요소는 모두 공통 지점$($으로 α${\displaystyle$ \alpha$$$}$ - fixed point)에서 접촉합니다.이러한 $구성{\displaystyle {}_{}}$ ${\displaystyle {요소}_{}}$에 U 0${\displaystyle ,}$…, ${\displaystyle {U\mathrm{q}}_{}}$ - 1$${\$displaystyle$ U_${0},\dots,U_{q-1}$라고 반시계 방향으로 레이블을 지정하면 ${\displaystyle {fc}_{}}${\$displaystyle f_{c}$가 구성 $요소{\displaystyle {}_{}}$ ${\displaystyle {Uj}_{}}${\$displaystyle$ U_${j}$를 구성 $요소{\displaystyle {}_{}}$ ${\displaystyle {Uj}_{}}$ ${\displaystyle {+p}_{}}$ (${\displaystyle {\mathrm{mod}q)}_{}}$ ${\$q$)\}$에 매핑합니다.

${\displaystyle {\frac{\mathrm{cp}}{}}_{}}$q {\$displaystyle c_{\frac {p}{q}}$에서 발생하는 동작의 변화를 분기라고 합니다. 끌어당기는 고정 지점이 반발 주기-q 사이클과 "충돌"합니다.분기 매개 변수를 ${\displaystyle \frac{\mathrm{pq}}{}}${\$displaystyle${\$tfrac {p}{q}}$ - $전구$로 통과하면 끌어당기는 고정점이 반발 고정점($\alpha {\displaystyle }${\$displaystyle \alpha}$ - 고정점$$)으로 바뀌고 주기-q 사이클이 매력적이 됩니다.

쌍곡선 구성 요소

$지도{\displaystyle {}_{}}$ ${\displaystyle {fc}_{}}$ ${\$가 매력적인 주기를 갖는 만델브로 집합의 내부 구성 요소인 전구를 쌍곡선 ^{[citation needed]}구성 요소라고 합니다.

이들은 M {\$displaystyle$ $}$의 유일한 내부$$영역이며 M {\$displaystyle$ M$\}$에서 밀도가 높을 것으로 추측됩니다. 쌍곡선 밀도로 알려진 이 문제는 복잡한 ^[17]역학에서 가장 중요한 열린 문제 중 하나입니다.만델브로 집합의 가상적인 쌍곡선이 아닌 구성 요소는 종종 "퀴어"^[18][19] 또는 고스트 구성 요소라고 합니다.실수 이차 다항식의 경우, 이 질문은 1990년대에 류비치와 그라치크와 ś위텍에 의해 독립적으로 증명되었습니다. (실축과 교차하는 쌍곡 성분은 파이겐바움 도표에서 주기적 창과 정확히 일치합니다.따라서 이 결과는 이러한 창이 다이어그램의 모든 매개 변수 근처에 존재함을 나타냅니다.)

모든 쌍곡 구성요소가 만델브로 집합의 주요 심장부로부터 직접적인 분기에 의해 도달할 수 있는 것은 아닙니다.그러한 구성요소는 작은 만델브로 사본(아래 참조)의 주요 심장 박동으로부터 직접적인 분기에 의해 도달할 수 있습니다.

각 쌍곡 구성 요소에는 중심이 있으며, 이는 ${\displaystyle {fc}_{}z)}$ ${\displaystyle f_{c}(z)}$에 $대한{\displaystyle {}_{}}$ 내부 Fatou 도메인이 초매력 주기를 가지는 점 c입니다. 즉, 매력이 무한하다는 것입니다.이는 사이클에 임계점 0이 포함되어 있으므로 일부 반복 후 0이 다시 자신에게 반복된다는 것을 의미합니다.따라서 일부 n에 대해 ${\displaystyle {}_{}^{}}$n (${\displaystyle 0)}$ = ${\displaystyle 0}${\$displaystyle f_{c}^{n}(0$)=$0}$입니다.이 $다항식$을 ${\displaystyle {Qn}^{}}$(${\displaystyle c)}${\$displaystyle$ Q$^{n}(c)}$라고 하면 (z 대신 c에 의존한다고 가정하면) ${\displaystyle {Qn}^{}}$+ ${\displaystyle 1^{}}$(${\displaystyle c)}$ = ${\displaystyle {Qn}^{}}$ ${\displaystyle {}^{}{c}^{}}$ 2${\displaystyle {}^{}}$+ ${\displaystyle c}${\$displaystyle$ Q$^{n+1}(c$)=$Q^{n}(c)^{2}+c}$이며 ${\displaystyle {Qn}^{}c)}$ ${\displaystyle$ Q$^{n}(c)}$의 정도가 ${\displaystyle {\mathrm{2n}}^{}}$ ${\displaystyle {-}^{}}$ 1$${\$displaystyle$ 2$^{n-1$입니다.따라서, 쌍곡 성분의 중심을 구성하는 것은 $방정식$ Q${\displaystyle n^{}}$ (${\displaystyle c)}$ = ${\displaystyle 0,}$ ${\displaystyle n}$ = ${\displaystyle 1,}$ ${\displaystyle 2,}$ ${\displaystyle 3,}$ $...{\displaystyle$ Q$^{n}(c$) = $0,n$ = $1,2,3$를 연속적으로 풀면 가능합니다. 각 단계에서 생성되는 새로운 중심의 수는 Sloane의 OEIS: A000740에 의해 주어집니다.

로컬 연결

만델브로 집합은 국소적으로 연결된 것으로 추측됩니다.이 추측은 MLC(Mandelbrot local connected)로 알려져 있습니다.아드리앙 두아디와 존 H. 허바드의 연구에 따르면, 이 추측은 만델브로 집합의 단순한 추상적인 "집힌 원반" 모형을 만들어 낼 것입니다.특히 ^{[citation needed]}위에서 언급한 중요한 쌍곡선 추론을 암시할 것입니다.

장 크리스토프 요코즈의 연구는 모든 유한하게 재규격화할 수 있는 매개변수에서 만델브로 집합의 지역적 연결성을 확립했습니다. 즉, 대략적으로 말하면, 많은 작은 만델브로 ^[20]사본에만 포함된 것들입니다.그 이후 M {\$displaystyle$M$\}$의 $다른{\displaystyle }$ 많은 지점에서 로컬 연결성이 증명되었지만 완전한 추측은 여전히 열려 있습니다.

자기유사성

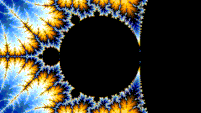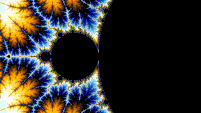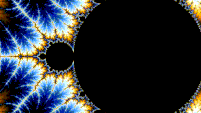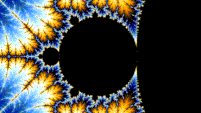
Mandelbrot 세트는 Misiurewicz 포인트 근처의 확대 하에 자체적으로 유사합니다.또한 한계 집합으로 ^[21][22]수렴한다는 의미에서 일반화된 파이겐바움 점(예를 들어 -1.401155 또는 -0.1528 + 1.0397i)을 중심으로 자기 유사한 것으로 추측됩니다.일반적으로 만델브로 집합은 임의의 작은 규모에서 약간 다른 버전의 자체를 찾을 수 있기 때문에 준자기 유사합니다.이 만델브로 세트의 복사본들은 모두 약간씩 다른데,^{[citation needed]} 주로 세트의 본체에 연결되는 얇은 실 때문입니다.

추후결과

만델브로 집합의 경계의 하우스도르프 차원은 시시쿠라 ^[23]미쓰히로의 결과로 결정된 2와 같습니다.이것이 위상 차원인 1보다 정수 전체만큼 크다는 사실은 만델브로 집합 경계의 극한 프랙탈 성질을 반영합니다.대략적으로 말하면, 시시쿠라의 결과는 만델브로 집합 경계가 너무 '위그글리'하여 2차원 평면 영역만큼 효율적으로 공간을 채웠다는 것입니다.하우스도르프 차원 2가 있는 곡선은 (위상적으로) 1차원임에도 불구하고 종종 0이 아닌 면적(더 공식적으로는 0이 아닌 평면 르베그 측도)을 가질 수 있습니다.이것이 만델브로 설정 경계의 경우인지 여부는 해결되지 않은 ^{[citation needed]}문제입니다.

고차원 초복소수 공간(즉, 반복 $변수{\displaystyle }$ z$${\$displaystyle$ z$}$의 $거듭제곱{\displaystyle }$ α$${\$displaystyle \alpha }$가 무한대로 경향이 있을 때)에서 일반화된 만델브로는 단위(${\displaystyle }$ ${\displaystyle \alpha }$ -1$$)-^[24]sphere에 수렴하는 것으로 나타났습니다.

In the Blum-실제 계산의 Shub-Smale 모델인 만델브로 집합은 계산할 수 없지만, 그 보어는 계산할 수 있습니다.많은 단순 객체(예: 지수 그래프)도 BSS 모델에서 계산할 수 없습니다.현재로서는 만델브로 집합이 계산 가능한 분석에 기초한 실제 계산 모델에서 계산 가능한지 여부는 알 수 없으며, 이는 "컴퓨터가 집합을 플롯팅한다"는 직관적인 개념에 더 밀접하게 부합합니다.허틀링은 쌍곡성 추측이 ^{[citation needed]}사실일 경우 이 모델에서 만델브로 집합을 계산할 수 있음을 보여주었습니다.

줄리아 세트와의 관계

만델브로 집합의 정의 결과, 주어진 점에서 만델브로 집합의 기하학과 해당 줄리아 집합의 구조 사이에는 밀접한 대응 관계가 있습니다.예를 들어 c의 값은 해당 Julia 집합이 연결된 경우에만 만델브로 집합에 속합니다.따라서 만델브로 집합은 연결된 줄리아 ^{[citation needed]}집합의 지도로 볼 수 있습니다.

이 원리는 사실상 만델브로 집합의 모든 심층 결과에서 활용됩니다.예를 들어, 시시쿠라는 만델브로 집합의 경계에 있는 조밀한 매개변수 집합의 경우, 줄리아 집합은 하우스도르프 차원 2를 가지며, 이 정보를 매개변수 ^[23]평면에 전달한다는 것을 증명했습니다.마찬가지로 Yoccoz는 줄리아 세트의 지역적 연결성을 먼저 증명한 후 해당 ^[20]매개변수에서 만델브로 세트에 대해 설정했습니다.

기하학.

p 및 q가 비교적 소수인 모든 $유리수{\displaystyle \frac{}{}}$ ${\tfrac {p}{$$q$$\}\}$에 대해 주기 q의 쌍곡 구성요소는 2 ${\displaystyle \frac{}{}}$q {\$tfrac {$2$\p p}{$q$\}\}$^[25]의 내각에 해당하는 심장의 가장자리의 한 지점에서 주 심장 박동에서 분기합니다.이 분기점에서 주 심장 박동에 연결된 만델브로 세트의 부분을 p/q-limb라고 합니다.컴퓨터 실험에 따르면 사지의 ${\displaystyle \frac{{}^{}}{}}$은 1 ${\displaystyle \frac{{q\mathrm{}}^{}}{}}$2 {\$displaystyle {\tfrac {1}{q^{$2$\}\}\}\}$처럼 0인 경향이 있습니다.알려진 가장 좋은 현재 추정치는 Yoccoz-불평등으로, 크기가 ${\displaystyle \frac{1}{}}$q {\$displaystyle${\$tfrac {1}{q$^{[citation needed]}처럼 0인 경향이 있음을 나타냅니다.

마침표 q 사지는 사지 상단에${\displaystyle }$q - ${\displaystyle 1}${\$displaystyle q-1}$ "안테나"가 있습니다.주어진 전구의 주기는 이러한 안테나를 세어 결정합니다.회전수의 분자인 p는 각 안테나를 사지에서 반시계 방향으로 1부터${\displaystyle }$q - ${\displaystyle 1}$ ${\displaystyle q-1}$까지 번호를 매기고 가장 짧은 안테나를 ^[25]찾아냅니다.

만델브로 집합의 파이

p/q축의 두께가 0이라는 것을 증명하기 위해 데이비드 볼은 1991년에 컴퓨터 실험을 수행하여 z${\displaystyle }$= -${\displaystyle \mathrm{34}}$ + i$$ε {\$displaystyle$ z = - ${\tfrac {$3}{4$}}$+ i\$varepsilon$$$ -$$ {\$displaystyle -{\tfrac {$3}{4$}}$가 ${\displaystyle 위치}$함)에 대해 $시리즈$가 발산하는 데 필요한 반복 횟수를 계산했습니다.z = - ${\displaystyle \frac{34}{}}$ ${\displaystyle$ z = - {\$tfrac {3}{4$의 정확한 값에 대해 영상 시리즈가 발산되지 않기 때문에 $작은$ε {\$displaystyle$\varepsilon$\}$에서 필요한 반복 횟수가 증가합니다. ε$${\$displaystyle \varepsilon}$의 값에 필요한 반복 횟수를 곱하면 π$${\$displaystyle$}의 근사치가 산출됩니다.$ε$$${\$displaystyle \varepsilon$}이$($가) 작을수록 좋아지는 \$pi$ }입니다$.$ 예를 들어 $ε$$${\$displaystyle \varepsilon}$ $=$ 0.0000001의 경우 반복 횟수는 31415928회이고 제품은 3.1415928회입니다.2001년, 아론 클레바노프(Aaron Klebanoff)는 볼의 ^[27]발견을 증명했습니다.

만델브로 집합의 피보나치 수열

이 절에서는 출처를 언급하지 않습니다. 신뢰할 수 있는 자료에 인용문을 추가하여 이 부분을 개선하는 데 도움을 주시기 바랍니다. 출처가 밝혀지지 않은 자료에 이의를 제기하여 제거할 수 있습니다.(2023년 7월) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

Fibonacci 시퀀스가 Mandelbrot 세트 내에 위치하고 주 심장율동과 Farey ^[28]다이어그램 사이에 관계가 있음을 알 수 있습니다.주 심장막을 디스크에 매핑하면 다음으로 큰 쌍곡 구성 요소에서 확장되고 이전에 선택된 두 구성 요소 사이에 위치한 더듬이의 양이 Fibonacci 시퀀스와 일치합니다.안테나의 양은 또한 Farey 다이어그램과 관련이 있으며 디스크 주변의 거리와 관련된 해당 분수 값 내의 분모 양과도 관련이 있습니다.이러한 분수 값 자체의 두 부분을 모두 ${\displaystyle \frac{13}{}}${\$displaystyle {\frac {$1}{3$}}$ 후에$$ $합하여{\displaystyle \frac{\mathrm{}}{}}$ 시퀀스 내에서 다음 쌍곡선 구성 요소의 위치를 생성할 수 있습니다.따라서, 1, 2, 3, 5, 8, 13, 21의 피보나치 수열은 만델브로 집합 내에서 찾을 수 있습니다.

확대/축소 시퀀스의 영상 갤러리

이 절에서는 출처를 언급하지 않습니다. 신뢰할 수 있는 자료에 인용문을 추가하여 이 부분을 개선하는 데 도움을 주시기 바랍니다. 출처가 밝혀지지 않은 자료에 이의를 제기하여 제거할 수 있습니다.(2023년 7월) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

Mandelbrot 세트의 경계는 이미지를 자세히 보거나 확대할수록 더 복잡한 세부사항을 보여줍니다.다음은 선택한 c 값으로 확대하는 영상 시퀀스의 예입니다.

첫 번째 이미지에 대한 마지막 이미지의 배율은 약 10¹⁰ 대 1입니다.일반적인 컴퓨터 모니터와 관련하여, 그것은 직경 4백만 킬로미터의 만델브로 세트의 한 부분을 나타냅니다.

• 

  시작. 연속적으로 색이 있는 환경의 만델브로 세트.

• 

  "해마 계곡"이라고도 불리는 "머리"와 "몸" 사이의 간격

• 

  왼쪽은 두 개의 나선형, 오른쪽은 "해마"

• 

  "해마"를 거꾸로

해마 "몸"은 각각 12개의 "말"로 구성된 두 그룹의 "말"과 한 개의 "말"로 구성된 25개의 "말"로 구성되어 있습니다.이 두 그룹은 만델브로 집합의 "윗손"의 두 "손가락" 때문에 변형된 것으로 볼 수 있습니다. 따라서 "말"의 수는 한 "해마"에서 다음 "말"로 2 증가합니다. "허브"는 미시우레비츠 점입니다."몸의 윗부분"과 "꼬리" 사이에는 "위성"이라고 불리는 만델브로 집합의 왜곡된 사본이 있습니다.

• 

  "해마꼬리"의 중심 끝은 미시우레비츠 지점이기도 합니다.

• 

  "꼬리"의 일부 – 전체 "꼬리"를 통하는 얇은 구조물로 구성된 경로는 하나뿐입니다.이 지그재그 경로는 꼬리의 안쪽과 바깥쪽 경계에 25개의 "스포크"가 있는 큰 물체의 "허브"를 지나갑니다. 따라서 만델브로 집합은 단순히 연결된 집합입니다. 즉, 구멍 주위에 섬이 없고 순환도로가 없다는 것을 의미합니다.

• 

  위성.두 개의 "해마 꼬리"는 위성이 가운데에 있는 일련의 동심원 왕관의 시작입니다.

• 

  각각의 왕관은 비슷한 "해마 꼬리"로 구성되어 있는데, 그 수는 위성의 환경에서 전형적인 현상인 2의 힘으로 증가합니다.나선형 중심으로 가는 독특한 경로는 인공위성을 심장 박동의 홈으로부터 "머리"의 "안테나"의 상단으로 통과시킵니다.

• 

  위성의 "안테나".2차 위성이 여러 개 있습니다.

• 

  위성의 "해마 계곡"입니다.처음부터 모든 구조가 다시 나타납니다.

• 

  이중 나선형과 "설사" – 처음의 두 번째 이미지와는 달리, 그것들은 "설사 꼬리"와 같은 구조로 구성된 부록을 가지고 있습니다. 이것은 n차 위성 환경에서 n+1개의 다른 구조의 전형적인 연결을 보여주는데, 여기서 가장 간단한 경우는 n=1입니다.

• 

  2차 위성을 가진 이중 나선은 - "해마"와 유사하게, 이중 나선은 "안테나"의 변형으로 해석될 수 있습니다.

• 

  부록의 바깥 부분에는 구조물의 섬들이 인식될 수 있습니다; 그것들은 Julia sets_c J와 같은 모양을 가지고 있습니다; 가장 큰 것은 오른쪽에 있는 "더블 훅"의 중앙에서 발견될 수 있습니다.

• 

  "더블 훅"의 일부.

• 

  섬.

• 

  섬 하나에 대한 세부사항.

• 

  나선형의 세부사항.

세 번째부터 마지막 단계의 섬은 무한히 많은 부분으로 구성되어 있는 것처럼 보입니다. 해당 Julia $set{\displaystyle {}_{}}$ ${\displaystyle J_{}}$ c$${\$displaystyle$ J_${c$그들은 작은 구조들로 연결되어 있어서, 전체가 단순히 연결된 집합을 나타냅니다.이 작은 구조물들은 이 배율로 알아보기에는 너무 작은 중심부의 위성에서 서로 만납니다.$해당{\displaystyle {}_{}}$ ${\displaystyle J_{}}$ c$${\$displaystyle$ J_${c}$에 대한 c$${\$displaystyle$ c$}$의 값은 이미지 중심이 아니지만, 만델브로 세트의 본체에 대한 상대적인 값은 6단계에 표시된 위성에 대한 이 이미지의 중심과 동일한 위치를 갖습니다.

내부구조

이 절에서는 출처를 언급하지 않습니다. 신뢰할 수 있는 자료에 인용문을 추가하여 이 부분을 개선하는 데 도움을 주시기 바랍니다. 출처가 밝혀지지 않은 자료에 이의를 제기하여 제거할 수 있습니다.(2023년 7월) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

만델브로 집합은 일반적으로 외부 경계 세부사항을 표시하여 렌더링되지만 경계 집합 내의 구조도 나타낼 수 있습니다.예를 들어, 주어진 c 값이 바인딩된 상태인지 또는 바인딩되지 않은 상태인지를 계산하는 동안 이 값이 도달하는 최대값을 해당 위치의 c 값과 비교할 수 있습니다.제곱합 방법을 사용하면 계산된 수는 max:(real^2 + 허수^2) - c:(real^2 + 허수^2)가 됩니다.이 계산의 크기는 그래디언트 상의 값으로 렌더링될 수 있습니다.

이렇게 하면 경계에 접근함에 따라 뚜렷한 가장자리와 등고선을 가진 다음과 같은 결과가 나타납니다.애니메이션은 그라디언트 경계를 강조하는 역할을 합니다.

• 

  만델브로 집합 내의 애니메이션 구배 구조

• 

  Mandelbrot 세트 내부의 애니메이션 구배 구조

• 

  285에서 약 200,000까지의 점진적 반복을 애니메이션화된 해당 경계 그라디언트로 렌더링

• 

  점진적 반복에서 그라데이션을 위한 축소판

일반화

멀티브로트 세트

다중 브로트 집합은 복소 평면에서 일반 일변량 다항식 재귀 패밀리의 멤버에 대해 발견된 유계 집합입니다.

${\displaystyle z}$ ${\displaystyle \mapsto }$ ${\displaystyle z^{}}$d + ${\displaystyle c}$ ${\displaystyle$ z$\maps to$ z$^{d}$ +$c$

정수 d의 경우, 이 집합들은 동일한 공식으로 구축된 줄리아 집합에 대한 연결 로씨입니다.전체 입방정 연결 궤적도 연구되었습니다. 여기서 두 개의 임계점이 매개 변수 k의 복잡한 제곱근인 두 매개 변수 $재귀$ z ↦ ${\displaystyle z^{}}$ 3${\displaystyle {}^{}}$+ ${\displaystyle 3}$ ${\displaystyle \mathrm{kz}}$+ ${\displaystyle c}$ ${\displaystyle$ z$\mapsto$ z$^{3}$ + 3 $kz$+$c$를 고려합니다.두 임계점이 모두 ^[29]안정적인 경우 모수는 입방정맥락에 있습니다.동형 함수의 일반적인 계열의 경우, 만델브로 집합의 경계는 분기 ^{[citation needed]}위치로 일반화됩니다.

다중 브로트 집합은 지수 d의 값을 변경함으로써 얻어집니다.기사에는 d = 0에서 7까지의 전개를 보여주는 비디오가 있으며, 이때 둘레 주위에는 6개의 (${\displaystyle d}$- ${\displaystyle 1)}${\$displaystyle (d-1)}$개의 로브가 있습니다$.$일반적으로, d가 양의 정수일 때, 이들 세트 각각의 중심 영역은 항상 (${\displaystyle d}$- ${\displaystyle 1)}${\$displaystyle (d-1)}$개의$$ 커스텀들의${\displaystyle }$에피사이클로이드입니다.음의 적분 지수를 사용한 유사한 전개는 링 내부에서 (${\displaystyle 1}$- ${\displaystyle d)}${\$displaystyle ($1 -$$d)}개의$$ 갈라짐을${\displaystyle }$초래하며, 여기서 집합의 주요 중심 영역은 (${\displaystyle 1}$ ${\displaystyle -}$ ${\displaystyle d)}${\$displaystyle (1$ - d$)}$개의${\displaystyle }$^{[citation needed]}커스프의 하이포클로이드입니다.

고차원

3D로 설정된 만델브로의 완벽한 확장은 없습니다. 왜냐하면 만델브로가 반복할 수 있는 복잡한 숫자의 3D 아날로그가 없기 때문입니다.복잡한 숫자들이 4차원, 즉 쿼터니언으로 확장되어 만델브로 집합이 완벽하게 확장되고 줄리아 집합이 ^[30]4차원으로 확장됩니다.그런 다음 이들을 횡단하거나 3D 구조물에 투영할 수 있습니다.4차원 만델브로 집합은 (j-k 평면에서) 2차원 만델브로 집합의 혁명의 고체일 뿐이므로 ^[30]보기에 흥미롭지 않습니다.d =${\displaystyle 0}$ ( ${\displaystyle q}$ =${\displaystyle }$a + ${\displaystyle \mathrm{bi}}$ ${\displaystyle +}$ ${\displaystyle \mathrm{cj}}$+ ${\displaystyle d}$k )$${\$displaystyle$ d=$0\$ (q =$a$ +$bi$ +$dj$ + $dk)}$에서 3차원 단면을 취하면 실제 축을 중심으로 설정된 2차원 만델브로의 회전 입체가 생성됩니다.

기타 비분석 매핑

이 절에서는 출처를 언급하지 않습니다. 신뢰할 수 있는 자료에 인용문을 추가하여 이 부분을 개선하는 데 도움을 주시기 바랍니다. 출처가 밝혀지지 않은 자료에 이의를 제기하여 제거할 수 있습니다.(2023년 7월) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

특히 흥미로운 것은 반동형 가군의 연결 위치인 삼뿔 프랙탈입니다.

${\displaystyle }$z ${\displaystyle \mapsto }$ ${\displaystyle {}^{}}$ ¯ ${\displaystyle 2^{}}$+ ${\displaystyle c}${\$displaystyle$ z$\maps$ to {\$bar {z}}^{2}+c$입니다.

밀너는 실제 입방다항식의 매개변수 절편에 대한 연구에서 트리콘(때로는 만델바라고도 함)을 접했습니다.로컬로 연결되어 있지 않습니다.이 속성은 실수 입방 다항식의 연결 궤적에 의해 상속됩니다.

또 다른 비분석적 일반화는 버닝 쉽 프랙탈(Burning Ship fractal)이며, 다음을 반복하여 얻을 수 있습니다.

${\displaystyle z}$ ${\displaystyle \mapsto }$ (${\displaystyle \Re }$ (${\displaystyle z}$) ${\displaystyle +}$ ${\displaystyle i}$ℑ (${\displaystyle z^{}}$) 2${\displaystyle {}^{}}$+ ${\displaystyle c}${\$displaystyle$z\$mapsto$( \$Re$\left$(z\right))$ +$i$ \$I$\left$(z\right))^{2}$ +$c$

컴퓨터도면

이 절에서는 출처를 언급하지 않습니다. 신뢰할 수 있는 자료에 인용문을 추가하여 이 부분을 개선하는 데 도움을 주시기 바랍니다. 출처가 밝혀지지 않은 자료에 이의를 제기하여 제거할 수 있습니다.(2023년 7월) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

컴퓨팅 장치를 통해 만델브로 세트를 플롯하는 다양한 알고리즘이 존재합니다.여기서 가장 널리 사용되고 가장 간단한 알고리즘, 즉 순진한 "탈출 시간 알고리즘"이 설명될 것입니다.탈출 시간 알고리즘에서는 플롯 영역의 각 x, y 점에 대해 반복 계산을 수행하고 해당 계산의 동작을 기반으로 해당 픽셀에 대해 색상을 선택합니다.

각 점의 x 및 y 위치는 반복 또는 반복 계산에서 시작 값으로 사용됩니다(아래 자세히 설명).각 반복의 결과는 다음의 시작 값으로 사용됩니다.이 값은 각 반복 중에 중요한 "탈출" 상태에 도달했는지 또는 "구제금융" 상태에 도달했는지 여부를 확인하기 위해 확인됩니다.이 조건에 도달하면 계산이 중지되고 픽셀이 그려지며 다음 x, y 지점이 검사됩니다.

각 점의 색상은 값이 탈출점에 도달하는 속도를 나타냅니다.반복 제한 이전에 빠져나가지 못하는 값을 표시하기 위해 검은색을 사용하는 경우가 많고, 빠져나가는 점에는 점차 밝은 색을 사용합니다.탈출 조건에 도달하기까지 얼마나 많은 사이클이 필요했는지를 시각적으로 표현합니다.

이러한 이미지를 렌더링하기 위해 우리가 고려하고 있는 복소 평면의 영역을 일정 개수의 픽셀로 세분화합니다.이러한 픽셀을 색칠하려면 c ${\displaystyle$ c$}$을(를) 해당 픽셀의 중간점이라고 $합니다{\displaystyle }$.${\displaystyle {fc}_{}}${\$displaystyle f_{c$ $아래$에서 임계점 0을 반복하여 궤도 지점의 반경이 2보다 큰지 각 단계에서 확인합니다.이 경우 c ${\displaystyle$ c$}$은(는) 만델브로 집합에 속하지 않으며, 확인하는 데 사용된 반복 횟수에 따라 픽셀을 색칠합니다.그렇지 않으면 고정된 수의 단계까지 계속 반복하고, 그 후에 매개 변수가 만델브로 집합에서 "아마도" 또는 적어도 그에 매우 가깝다고 판단하여 픽셀을 검은색으로 색칠합니다.

의사 코드에서 이 알고리즘은 다음과 같이 보입니다.알고리즘은 복소수를 사용하지 않으며, 복소수 데이터 유형이 없는 사람들을 위해 두 개의 실수를 사용하여 복소수 연산을 수동으로 시뮬레이션합니다.프로그래밍 언어에 복잡한 데이터 형태의 연산이 포함되어 있다면 프로그램은 단순화될 수 있습니다.

화면의 각 픽셀(Px, Py)에 대해 x0 := 픽셀의 스케일 x 좌표(Mandelbrot X 스케일(-2.00, 0.47)) y0 := 픽셀의 스케일 y 좌표(Mandelbrot Y 스케일(-1.12, 1.12)) x := 0.0 y : = 0.0 반복 : = 0 max_limit : = 1000인 반면 (x*x + y*y ≤ 2*2) 반복 < max_limit> 반복 : = x*x - y*y + x0 y : = 2*x*y + y0 x : = xtemp 반복 : = 반복 + 1

색상 : = 팔레트[색상] 그림(Px, Py, color)

여기서 의사 코드를 c$${\$displaystyle$c$\},$ $z{\displaystyle }${\$displaystyle$ z$}$ $및$ ${\displaystyle {fc}_{}}${\$displaystyle f_{c$에 연관시킵니다.

• ${\displaystyle z=x+iy}$
• ${\displaystyle z^{2}=x^{2}+i2xy-y^{2}}$
• ${\displaystyle c=x_{0}+iy_{0}}$

따라서 x와 y의 계산에서 의사코드에서 볼 수 있듯이,

• ${\displaystyle x}$ ${\displaystyle =\mathrm{Re}}$ ${\displaystyle }$ ( ${\displaystyle z^{}}$2 +${\displaystyle c}$ ) ${\displaystyle =}$ ${\displaystyle x^{}{}^{}}$ - ${\displaystyle y^{}}$2 + ${\displaystyle {}_{}}$ ${\displaystyle 0_{}}${\$displaysty$ x=\$mathrm {Re}}$ ($z$$^{2}$ +${\displaystyle }$c) ${\displaystyle =}$ $x^{2}$ - $y^{2}$ + $x_{0}$ $y$ ${\displaystyle =}$ ${\displaystyle \mathrm{I}}$ ${\displaystyle }$ ( ${\displaystyle 2^{}}$ +${\displaystyle }$${\displaystyle c}$ ) = ${\displaystyle 2}$ ${\displaystyle x}$y + ${\displaystyle {}_{}}$ ${\displaystyle 0_{}}${\$displaysty$${\displaystyle l}$$e$ y=\$mathrm {$${\displaystyle I}$$m}$=$2xy$+$y_{0$입니다.

다양한 함수(선형, 지수 등) 중 하나를 사용하여 실행된 반복 횟수의 각 값에 컬러를 할당하여 세트의 컬러 이미지를 얻을 수 있습니다.

대중문화 관련 참고문헌

만델브로 세트는 가장 인기 있는 ^[31][32]프랙탈로 널리 여겨지고 대중문화에서 여러 번 언급되었습니다.

• 조나단 콜튼의 노래 "Mandelbrot Set"는 프랙탈 그 자체와 그 이름을 딴 남자 Benoit Mandelbrot에게 ^[33]바치는 곡입니다.
• 블루맨 그룹의 1999년 데뷔 앨범에 수록된 여러 트랙 타이틀인 오디오는 만델브로 세트를 참조합니다.이것들은 "오프닝 만델브로", "만델그루브", 그리고 "클라인 만델브로"^[34] 입니다.
• Piers Anthony의 Mode 시리즈의 두 번째 책인 Fractal Mode는 세트의 ^[35]완벽한 3D 모델인 세계를 묘사합니다.
• 아서 C. 클라크의 소설 그랜드 뱅크스에서 온 유령은 만델브로 세트의 모양을 ^[36]모방하여 만들어진 인공 호수를 특징으로 합니다.
• 2020년 11월 20일(고 브누아 만델브로의 96번째 생일)^[37]에 구글 두들의 소재가 된 베누아 만델브로와 동명의 세트.
• 미국의 록 밴드 Heart는 2004년 앨범 Jupiters Darling의 표지에 만델브로의 이미지를 실었습니다.
• 영국 블랙 메탈 밴드 아나알 나트라흐는 에샤톤 앨범 커버 아트에 만델브로 세트와 비슷한 이미지를 사용합니다.
• 텔레비전 시리즈인 Dirk Sently's Holistic Detective Agency (2016)는 아만다라는 캐릭터의 환영과 관련된 만델브로를 두드러지게 등장시킵니다.두 번째 시즌에서 그녀의 재킷은 뒷면에 ^[38]프랙탈의 큰 이미지를 가지고 있습니다.
• Ian Stewart의 2001년 저서인 Plattleland에는 Mandelblot이라 불리는 인물이 있는데, 그는 등장인물과 ^[39]독자들에게 프랙탈을 설명하는 것을 돕습니다.
• 완성되지 않은 Alan Moore 1990년 만화책 시리즈 Big Numbers는 그 작품의 구조를 뒷받침하기 위해 프랙탈 기하학과 혼돈 이론에 대한 Mandelbrot의 연구를 사용했습니다.무어는 어느 순간 만화책 시리즈인 만델브로 ^[40]세트라는 이름으로 가고 있었습니다.
• 만화 여름 히카루가 죽었다에서 요시키는 거짓 히카루의 몸에 닿았을 때 만델브로 세트를 환각에 빠트립니다.

참고 항목

참고문헌

추가열람

• Milnor, John W. (2006). Dynamics in One Complex Variable. Annals of Mathematics Studies. Vol. 160 (Third ed.). Princeton University Press. ISBN 0-691-12488-4.
  (1990년에 Stony Brook IMS Preprint로 처음 등장했으며 arXiV:math.DS/9201272로 사용 가능)
• Lesmoir-Gordon, Nigel (2004). The Colours of Infinity: The Beauty, The Power and the Sense of Fractals. Clear Press. ISBN 1-904555-05-5.
  (Arthur C가 수록된 DVD 포함). 클라크와 데이비드 길모어)
• Peitgen, Heinz-Otto; Jürgens, Hartmut; Saupe, Dietmar (2004) [1992]. Chaos and Fractals: New Frontiers of Science. New York: Springer. ISBN 0-387-20229-3.

외부 링크

• 컬리의 혼돈과 프랙탈
• 비디오: Mandelbrot fractal zoom 6.066 e228
• 수학적 과정에 대한 비교적 간단한 설명, 홀리 크리거 박사, MIT
• Mandelbrot Viewer : 예제가 있는 갤러리를 포함하는 브라우저 기반의 Mandelbrot 세트 렌더러.
• (Rosetta Code에서) Mandelbrot 집합을 계산하기 위한 다양한 알고리즘
• 불가리아 소피아 데얀 도브로미로프가 루아로 쓴 프랙탈 계산기