옥토니언

옥토니언스
옥토니언스
기호
유형	하이퍼콤플렉스 대수학
단위	e0, ..., e7
승수정체성	e0
주특성	비약속; 비연관적
공통 시스템
	자연수; 정수; 이성수; 실수; 콤플렉스; 쿼터니온스; show 덜 일반적인 시스템

수학에서, 옥톤수는 실제 숫자에 대한 표준 분할 대수로서, 일종의 하이퍼 복합 수 체계다. 8진법은 대담한 얼굴 $O$ 나 칠판 $\mathbb {O}$ 한 O ${\$ 을 사용하여 보통 대문자 O로 표현된다 $\mathbb {O}$ 8진법은 4진법 치수의 두 배인 확장형 치수를 갖는다. 그들은 비협조적이고 비협조적이지만, 약한 형태의 연대를 만족시킨다. 즉, 그들은 대안이다. 그들은 또한 권력 연상이다.

옥토니언은 쿼터니언이나 복잡한 숫자로 잘 알려져 있지 않은데, 이것은 훨씬 더 널리 연구되고 사용된다. 옥토니언은 수학에서 예외적인 구조와 관련이 있는데, 그중에서도 예외적인 리 집단이다. 옥톤은 끈 이론, 특수 상대성, 양자 논리 같은 분야에 응용이 있다. 케이리-딕슨 구조를 옥토니언에 적용하면 진정제가 생성된다.

역사

옥톤은 1843년 존 T. 그레이브스에 의해 발견되었는데, 그의 친구 윌리엄 로완 해밀턴의 쿼터니온의 발견에서 영감을 받았다. 그레이브스는 자신의 발견을 "옥타브스"라고 불렀고, 1843년 12월 26일자 해밀턴에게 보낸 편지에서 이를 언급하였다. 그는 처음으로 아서 케이리의 기사보다 약간 늦게 결과를 발표했다.^[2] 8진법은 케이리^[3](Cayley)에 의해 독립적으로 발견되었으며, 때때로 "케이리 숫자" 또는 "케이리 대수"로 언급되기도 한다. 해밀턴은 그레이브스의 발견 초기 역사를 묘사했다.^[4]

정의

옥톤은 실수의 8진수(또는 8진수)로 생각할 수 있다. 매 옥토니언은 단위 옥토니언의 실제 선형 조합이다.

\{e_{0},e_{1},e_{2},e_{3},e_{4},e_{5},e_{6},e_{7}},

여기서 $e$ 는₀ 스칼라 또는 실제 요소로서, 실제 숫자 1과 동일할 수 있다. 즉, 모든 옥토니언 $x$ 는 양식으로 쓸 수 있다.

x=x_{0}e_{0}+x_{1}e_{1}+x_{2}e_{2}+x_{3}e_{3}+x_{4}e_{4}+x_{5}e_{5}+x_{5}+x_{6}e_{6}+x_{7}e_{7},\,

실제 계수 $x$ 를_i 사용하여

8진법의 덧셈과 뺄셈은 해당 항과 그에 따른 계수를 쿼터니언과 같이 더하고 빼는 것으로 이루어진다. 곱셈은 더 복잡하다. 곱셈은 덧셈보다 분배적이기 때문에, 다시 쿼터니온처럼 모든 조건의 곱을 합하여 2 옥톤의 곱을 계산할 수 있다. 각 항 쌍의 산물은 다음과 같이 계수 곱셈과 단위 옥토니언의 곱셈표를 통해 얻을 수 있다(Cayley, 1845년 및 Graves, 1843년).^[5]

$e_{i}e_{j}}$		$e_{j}$
$e_{i}e_{j}}$		$e_{0}$	${\displaystyle e_{1}.$	${\displaystyle e_{2}}:$	$e_{3}$	$e_{4}$	$e_{5}$	$e_{6}$	$e_{7}$
$e_{i}$	$e_{0}$	$e_{0}$	${\displaystyle e_{1}.$	${\displaystyle e_{2}}:$	$e_{3}$	$e_{4}$	$e_{5}$	$e_{6}$	$e_{7}$
	${\displaystyle e_{1}.$	${\displaystyle e_{1}.$	$-e_{0}$	$e_{3}$	${\displaystyle -e_{2}}:$	$e_{5}$	$-e_{4}$	$-e_{7}$	$e_{6}$
	${\displaystyle e_{2}}:$	${\displaystyle e_{2}}:$	$-e_{3}$	$-e_{0}$	${\displaystyle e_{1}.$	$e_{6}$	$e_{7}$	$-e_{4}$	$-e_{5}$
	$e_{3}$	$e_{3}$	${\displaystyle e_{2}}:$	$-e_{1}:{1$	$-e_{0}$	$e_{7}$	$-e_{6}$	$e_{5}$	$-e_{4}$
	$e_{4}$	$e_{4}$	$-e_{5}$	$-e_{6}$	$-e_{7}$	$-e_{0}$	${\displaystyle e_{1}.$	${\displaystyle e_{2}}:$	$e_{3}$
	$e_{5}$	$e_{5}$	$e_{4}$	$-e_{7}$	$e_{6}$	$-e_{1}:{1$	$-e_{0}$	$-e_{3}$	${\displaystyle e_{2}}:$
	$e_{6}$	$e_{6}$	$e_{7}$	$e_{4}$	$-e_{5}$	${\displaystyle -e_{2}}:$	$e_{3}$	$-e_{0}$	$-e_{1}:{1$
	$e_{7}$	$e_{7}$	$-e_{6}$	$e_{5}$	$e_{4}$	$-e_{3}$	${\displaystyle -e_{2}}:$	${\displaystyle e_{1}.$	$-e_{0}$

표의 대부분의 비대각 원소들은 대칭성이기 때문에 대칭 대칭에 있는 원소뿐만 아니라 $e$ 가₀ 피연산자인 행과 기둥을 제외하면 거의 대칭성이 된다.

표는 다음과 같이 요약할 수 있다.^[6]

{\displaystyle e_{i}e_{j}={\case}e_{j},&\text{{nif }i=0\\e_{i},&\text{nif }j=0\-\i}, }{ij}e}e_+\varepsilon_{k}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}.

여기서 $Δ$ 는_ij Kronecker delta ( $i$ = $j일$ 경우에만 1과 같음)이며_ijk, $Δ는 ijk$ = 123, $145, 176, 246, 257$ , 347, 365일 때 값이 1인 완전한 대칭 텐서이다.

그러나 위의 정의는 고유하지 않다; $e 0$ = $1$ 을 가진 팔손 곱셈에 대해 가능한 정의 480개 중 하나일 뿐이다. 다른 것들은 비스칼라 기본 요소 { $e 1,$ e, $e 2 3,$ $e 4 5,$ $e 6,$ $e 7}$ 의 기호를 허용하고 변경함으로써 얻을 수 있다. 480개의 서로 다른 알헤브라는 이질형이며, 어떤 특정한 곱셈 규칙이 사용되는지 고려할 필요가 거의 없다.

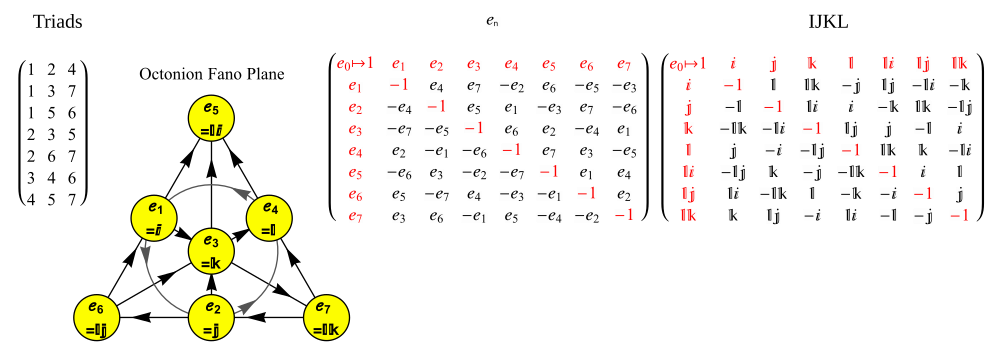
이 480개 정의 각각은 포인트의 7주기(1234567)에 따라 부호까지 불변하며, 각 7주기마다 부호와 순서 번복에 따라 다른 4개의 정의가 있다. 일반적인 선택은 $ee 12$ = $e 4$ —와 함께 7주기(134567)에 따라 삼각 구획도를 사용하거나, 또는 아래 Fano 평면에 124 기반 7주기 트라이애드 및 관련 구획 매트릭스의 $정렬 n$ 목록을 e와 IJKL 형식으로 표시하는 것이다.

Octonion triads, Fano plane, and multiplication matrices

때때로 사용되는 이것의 변화는 유한한 순서 7에 걸쳐 투사선 line $,$ 0, 1, 2, ..., 6의 원소에 기초 원소에 라벨을 붙이는 것이다. 그런 다음 곱셈은 $e \infty$ = $1$ 과₁₂ e = $e$ 로₄ 주어지며, 이를 통해 모든 첨자에 상수(모듈로 7)를 추가하여 얻은 모든 표현은 다시 말하면 7개의 삼배수(124)(235)(346)(450)(561) (602)(013)를 사용한다. 이것은 $GF$ ( $2)$ 라는 두 원소의 갈루아 필드 위에 길이 7의 2차 잔류 코드에서 0이 아닌 코드 워드들이다 $.$ 모든 첨자에 상수모드 7을 더하면 순서 7의 대칭성이 있고, 모든 첨자에 2차 잔류물 1, 2, 4차모드 7의 1을 곱하면 순서 3의 대칭성이 있다.^[7]^[8]

기호 $(----)$ 의 기하 대수 곱셈표는 다음과 같은 7쿼터니온 3배(ID요소 포함)의 관점에서 제시될 수 있다.

(I, j, k), (i, J, k), (i, j, k), (I, J, K), (* I, i, m), (* J, j, m), (* K, k, m), (*K, k, m)

여기서 소문자 항목은 벡터, 대문자 항목은 양각자 및 $*$ = $mijk$ (Hodge star operator)이다. 만약 $*$ 이 정체성과 같도록 강요된다면, 곱셈은 더 이상 연관성이 없어지지만,table은 곱셈표에서 제거되어 팔괘 곱셈표가 될 수도 있다.

$*$ = $mijk$ 연관성을 유지하여 4차원 기하학적 대수학을 8진수 1로 줄이지 않는 경우, 전체 곱셈표는 $*$ 에 대한 방정식에서 도출할 수 있다. 감마 행렬을 고려하십시오. 다섯 번째 감마 행렬을 정의하는 공식은 감마 행렬의 4차원 기하학적 대수algebra임을 보여준다.

케이리-딕슨 건설

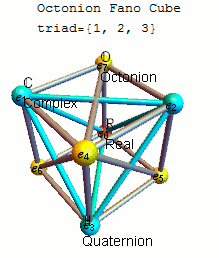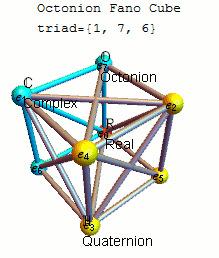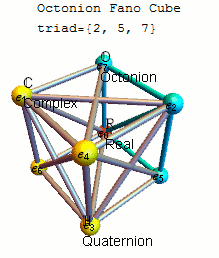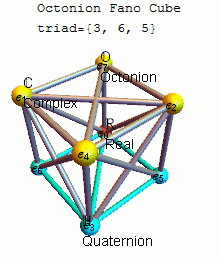
8진법을 정의하는 보다 체계적인 방법은 Cayley-Dickson 건설을 통해서이다. 쿼터니온이 복잡한 숫자의 쌍으로 정의될 수 있듯이, 팔분의 쌍은 쿼터니온의 쌍으로 정의될 수 있다. 추가는 쌍으로 정의된다. 두 쌍의 쿼터니온 $(a,$ $b)$ 및 $(c,$ $d)$ 의 곱은 다음과 같이 정의된다.

(a,b)(c,d)=(ac-d^{*}b,da+bc^{*}),

여기서 $z *$ 는 쿼터니언 $z$ 의 결합을 의미한다. 이 정의는 8단위 옥톤이 쌍으로 식별될 때 위에 주어진 정의와 동일하다.

(1, 0), (i, 0), (j, 0), (k, 0), (0, 1), (0, i), (0, j), (0, k)

파노 평면 니모닉

단위 옥토니언의 제품을 위한 니모닉.^[9]

위에 제시된 옥토니언 예제의 실제(

e 0

) 꼭지점을 통해 7개의 트라이애드를 하이퍼플레인으로 보여주는 3D 니모닉 시각화.^[9]

단위 옥토니언의 제품을 기억하기 위한 편리한 니모닉은 이 도표에 의해 제시되는데, 이 도표는 케이리와 그레이브스의 곱셈표를 나타낸다.^[5]^[10] 7개의 점, 7개의 선(원부터 1, 2, 3까지를 선으로 본다)이 있는 이 도표를 파노 평면이라고 한다. 그 선들은 방향성이 있다. 7점은 $임(O)$ 의 7가지 표준기준 요소에 해당한다(아래 정의 참조). 각각의 구별되는 점 쌍은 고유한 선에 놓여 있고 각 선은 정확히 세 점을 통과한다.

$(a,$ $b,$ $c)$ 는 화살표 방향에서 지정한 순서에 따라 주어진 선에 놓여 있는 점의 3배 순서가 되도록 한다. 그러면 곱셈은 다음에 의해 주어진다.

ab

= c

및

ba

=

-c

순환 순열과 함께 이 규칙들은 와 함께.

1은 승수 정체성,
$e 2 i$ = 다이어그램의 각 점에 대해 $-1$

옥토니언의 승법 구조를 완전히 규정한다. 7개의 선 각각은 쿼터니온 $H$ 에 $대해$ O 이형성의 아발지브라(subalgebra를 생성한다.

공법, 표준 및 역법

옥토니언의 결합

x=x_{0}\,e_{0}+x_{1}\,e_{1}+x_{2}\,e_{2}+x_{3}\,e_{3}+x_{4}\,e_{4}+x_{5}\,e_{5}+x_{6}\,e_{6}+x_{7}\,e_{7}

에 의해 주어지다

x^{*}=x_{0}\,e_{0}-x_{1}\,e_{1}-x_{2}\,e_{2}-x_{3}\,e_{3}-x_{4}\,e_{4}-x_{5}\,e_{5}-x_{6}\,e_{6}-x_{7}\,e_{7}.

결합은 $O$ 의 비자발이며( $xy)*$ = $y * x *($ 순서의 변화에 유의)를 만족한다.

$x$ 의 실제 부분은 다음에 의해 주어진다.

{\frac {x+x^{*{2}}:}=x_{0}\,e_{0}}

그리고 상상의 부분 by

{\frac {x-x^{*}}{2}}=x_{1}\,e_{1}+x_{2}\,e_{2}+x_{3}\,e_{3}+x_{4}\,e_{4}+x_{5}\,e_{5}+x_{6}\,e_{6}+x_{7}\,e_{7}.

모든 순전히 상상의 옥톤 세트는 7차원 $O$ 의 하위 공간에 걸쳐 $있으며$ , 임 $(O$ )으로 표시된다 $.$

옥토니언의 결합은 방정식을 만족시킨다.

x^{*}=-{\tfrac {1}{6}}{\bigl (}x+(e_{1}x)e_{1}+(e_{2}x)e_{2}+(e_{3}x)e_{3}+(e_{4}x)e_{4}+(e_{5}x)e_{5}+(e_{6}x)e_{6}+(e_{7}x)e_{7}{\bigr )}.

그 결합이 있는 옥토니언의 $곱인$ x* $x$ = $xx *$ 는 항상 음이 아닌 실수다.

x^{*}x=x_{0}^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}+x_{5}^{2}+x_{6}^{2}+x_{7}^{2}.

이를 이용하여 다음과 같이 옥토니언의 규범을 정의할 수 있다.

\ x\ ={\sqrt {x^{*}x}}.

이 표준은 $R$ 의⁸ 표준 8차원 유클리드 규범과 일치한다.

$O$ 에 표준이 존재한다는 것은 $O$ 의 모든 0이 아닌 원소에 대한 역의 존재를 암시한다. $xx -1$ = $xx -1$ = $1$ 을 만족하는 고유한 옥토니언 $x$ 인⁻¹ x ≠ $0$ 의 역은 다음과 같이 주어진다.

x^{-1}={\frac {x^{*}{\x\ ^{2}}.

특성.

8진법 곱셈은 상쇄적이지 않다.

ee i j

=

-ee j i ee j i

i, j가

구별

되고 0이 아닌 경우

연관성이 없는 경우:

(ee i j) e k

=

-e i (ee j k)

≠

e i (ee j k)

i

,

j

,

k

가 구별되는 경우, non-zero 및

ee i j

\neq

±

e k

.

8분의 1은 더 약한 형태의 연관성을 만족시킨다: 그들은 대안이다. 이것은 어떤 두 가지 원소에 의해 생성되는 하위 지브라도 연관성이 있다는 것을 의미한다. 실제로 $O$ 의 어떤 두 원소에 의해 생성되는 아발지브라(subalgebra)가 $R$ , $C$ , $H$ 에 이형성이 있다는 것을 보여줄 수 있는데, 이 모든 것이 연관성이 있다. 이들의 비연관성 때문에 옥톤은 $\mathbb {R}$ 숫자, 복잡한 숫자 및 쿼터니언과는 달리 R ${\$ 위에 있는 행렬 링의 하위 게이지로 나타낼 수 없다 $\mathbb {R}$

8진법은 $R$ , $C$ , $H$ 가 공유하는 하나의 중요한 속성을 유지한다: $O$ 에 대한 표준은 충족한다.

\displaystyle \ xy\ =\ x\ \ y\ .}

이 방정식은 8진법이 구성대수를 형성한다는 것을 의미한다. 케이리-딕슨 건설에 의해 정의된 고차원 알헤브라는 모두 이 성질을 만족시키지 못한다. 그들은 모두 0개의 칸막이들을 가지고 있다.

더 넓은 수의 시스템이 존재하며, 여기에는 승법계(예: 16차원 원뿔 침전)가 있다. 그들의 계수는 그들의 규범과 다르게 정의되어 있고, 또한 0점수를 포함하고 있다.

허위츠가 보여주듯이 $R$ , $C$ , $H$ , $O$ 는 실수에 대해 유일하게 규범화된 디비전 알헤브라이다. 이 네 개의 알헤브라는 실수에 대한 유일한 대안인 유한차원 분할 알헤브라를 형성하기도 한다.

$O$ 의 0이 아닌 원소는 연관성이 없어 집단을 형성하지 않는다. 그러나 그들은 루프를 형성하는데, 특히 무방 루프를 형성한다.

정류자 및 교차 제품

2 옥토니언 $x$ 와 y의 정류자는 다음과 같이 주어진다.

[x,y]=xy-yx.

이것은 비대칭이며 가상이다. 상상적 $아공간$ 에서만 상품으로 간주되는 경우, 그것은 그 공간, 즉 7차원 교차상품(Im $(O)$ 에 대해 다음과 같이 정의한다.

x\property y={\tfrac {1}{2}}(xy-yx).

3차원의 교차 제품과 마찬가지로 이것은 $x$ 와 $y$ 에 직교하는 벡터다.

\displaystyle \ x\board y\ =\ x\ \sin \theta.}

그러나 옥토니언 제품처럼 그것은 독특하게 정의되지 않는다. 대신 여러 가지 교차 제품이 있는데, 각 교차 제품은 옥토니언 제품의 선택에 따라 다르다.^[11]

자동형성

옥토니언의 자동형성 $A$ 는 $O$ 를 만족시키는 반전 불가능한 선형 변환이다.

[\displaystyle A(xy)=A(x)A(y)]}

$O$ 의 모든 자동화 집합은 $G$ 라고₂ 불리는 그룹을 형성한다.^[12] $G 2$ 그룹은 단순하게 연결되고 컴팩트하며 실제 Lie 그룹인 차원 14이다. 이 그룹은 예외적인 리 그룹 중 가장 작은 그룹이며, 8차원 실제 스피너 표현에서 선택된 특정 벡터를 $보존하는 스핀($ 7)의 하위 그룹과 이형성이다. $스핀(7)$ 그룹은 아래에 설명된 동위원소 그룹의 하위 그룹이다.

참고 항목: $PSL(2,7)$ – Pano 평면의 자동 형태 그룹을 참조하십시오.

동위원소

대수의 동위원소는 $xy$ = $z$ 인 $경우$ a $(x) b (y)$ = $c (z$ )와 같이 3배의 생체적 선형 지도 $a$ , b, $c$ 이다 $.$ $a$ = $b$ = $c$ 의 경우 이것은 자동형과 동일하다. 대수학의 동위원소 그룹은 모든 동위원소의 그룹이며, 부분군으로서의 자동화 그룹을 포함한다.

8진법의 동위원소 그룹은 $스핀 8 (R$ ) 그룹이며 $,$ 3개의 8차원 표현으로 작용하는 $a$ , $b$ , $c$ 를 가지고 있다.^[13] $c$ 가 정체성을 고정하는 원소의 부분군은 부분군 $스핀 7 (R$ )이고 $,$ $a$ , $b$ , $c$ 가 모두 정체성을 고정하는 부분군은 자동화 그룹 $G$ 이다₂.

적용들

8진법은 다른 수학 실체의 분류와 구성에서 중요한 역할을 한다. 예를 들어 예외적인 Lie $그룹 2$ G는 8진법의 자동형 그룹이며, 다른 예외적인 Lie 그룹 $F 4$ , E, $E 7$ , $E$ 는₆₈ 8진법을 사용하여 정의된 특정 투영 평면의 등각계로 이해할 수 있다.^[14] 대칭 매트릭스 제품이 장착된 자기 적응형 3 × 3 옥톤온 행렬 집합은 알버트 대수학을 정의한다. 이산수학에서 옥토니언은 리치 격자(Leech lattice)의 기초적인 유래를 제공하며, 따라서 산발적으로 단순한 집단과 밀접한 관계가 있다.^[15]^[16]

물리학에 대한 8분의 1의 적용은 대체로 추측이었다. 예를 들어, 1970년대에는 팔각형의 힐버트 공간을 통해 쿼크를 이해하려는 시도가 있었다.^[17] 옥토니언, 그리고 규범화된 분할 알헤브라가 4개만 존재할 수 있다는 사실은 초대칭 양자장 이론을 구성할 수 있는 스페이스타임 차원과 관련이 있는 것으로 알려져 있다.^[18]^[19] 또한, "Dixon $대수$ " $C$ ⊗ H $using$ O를 사용하는 등, 옥토니언 구조로부터 기초 입자 물리학의 표준 모델을 획득하려는 시도가 있었다.^[20]^[21]

블랙홀 엔트로피와 양자정보과학 연구에서도 옥톤이 발생했다.^[22]^[23]

옥토니언은 로봇공학에서 손 눈 교정 문제에 대한 해결책에 사용되어 왔다.^[24]

깊은 옥토니언 네트워크는 머신러닝 애플리케이션에서 효율적이고 압축적인 표현 수단을 제공한다.^[25]

적분 옥톤수

옥토니언의 일체형 형태를 선택하는 데는 몇 가지 자연스런 방법이 있다. 가장 간단한 것은 좌표가 정수인 8진법을 택하는 것이다. 이것은 그레이브스 옥토니언이라고 불리는 정수에 비 연상 대수학을 부여한다. 그러나 그것은 (링 이론의 의미로는) 최대 순서가 아니다; 정확히 7개의 최대 순서가 있다. 이 7가지 최대 주문은 모두 자동화 상태에서 동등하다. '통합 옥토니언스'라는 구절은 보통 이 일곱 가지 주문 중 하나를 고정적으로 선택하는 것을 말한다.

이러한 최대 주문은 Krefse(1925) 딕슨, 브루크(Bruck)에 의해 다음과 같이 구성되었다. 필드 위의 투영 선의 점을 기준으로 7개의 요소로 8개의 기본 벡터에 레이블을 붙인다. 첫 번째 형태 "Kirkese 정수": 이것들은 16개 세트 중 하나에서 좌표가 정수 또는 절반 정수인 1/2 정수인 8진수로 구성된다.

\emptyset (\infty124) (\infty235) (\infty346) (\infty450) (\infty561) (\infty602) (\infty013) (\infty0123456) (0356) (1460) (2501) (3612) (4023) (5134) (6245)

$\emptyset,$ $(\infty124)$ 및 상수 modulo 7을 추가하는 그것의 이미지와 이 8 세트의 보완이 주어지는 2개의 원소의 필드 위에 길이 8의 확장된 2차 잔류 코드. 그런 다음 무한대와 다른 좌표를 전환한다. 이 연산은 Kirkless 정수의 편차를 다른 세트로 만들어낸다. 이것은 최대 순서다. 이를 위한 7가지 방법이 있는데, 7개의 좌표 0123456의 주기적인 순열하에서는 모두 동등한 7개의 최대 명령을 내린다.(크리프스는 크라이프 정수도 역시 최대 순서를 형성한다고 잘못 주장했기 때문에 7개가 아니라 8개의 최대 순서가 있다고 생각했지만, 콕세터(1946)가 지적한 바와 같이 닫히지 않고 닫히지 않은 것은 아니다.err 곱하기; 이 실수는 여러 개의 출판된 논문에서 발생한다.)

크리케스 정수와 7개의 최대 주문은 모두 $E 8$ 격자의 등축이다. ½ ½. 특히 이들 주문에는 각각 최소 nonzero norm 1의 240개 원소가 있어 주문 240의 Moufang 루프를 형성하고 있다.

적분 옥톤은 "남은 구획" 특성을 가지고 있다. 적분 $옥톤수$ $a$ 와 b $0$ 0이 주어진 경우, $a$ = $qb$ + r로 $q$ 와 $r$ 을 찾을 수 있다. $여기$ 서 나머지 r은 $b$ 보다 규범이 적다.

일체형 옥토니언에서는 모든 왼쪽 이상과 오른쪽 이상이 양면 이상이며, 유일한 양면 이상은 $n$ 이 음이 아닌 정수인 주요 이상 $nO$ 이다.

적분 옥톤은 프리타임으로 인자화 버전을 가지고 있지만, 옥톤은 연관성이 없기 때문에 옥톤은 제품을 하는 순서에 따라 달라지기 때문에 설명하기가 쉽지 않다. 불분명한 적분 옥톤은 정확히 원시 표준의 옥톤이며, 모든 적분 옥톤은 불분명한 옥톤들의 산물로 쓰여질 수 있다. 보다 정확하게는 규범 $mn$ 의 일체형 옥토니언은 규범 $m$ 과 $n$ 의 일체형 옥토니언의 산물로 쓸 수 있다.

적분 옥토니언의 자동형성 그룹은 순서 12,096의 $그룹 2$ G $(F 2)$ 로, 단일 그룹 $A 2 (3 2$ )에 대해 지수 2의 단순 부분군을 가지고 있다 $.$ 일체형 옥토니언의 동위원소 $그룹$ 은₈ E 격자 회전 그룹의 완벽한 이중 커버다.

참고 항목

메모들

^ 사바디니, 아이린 등 “p 168.” Hypercomplex Analysis, Birkhauser, Basel, 2009, https://books.google.com/books?id=H-5v6pPpyb4C&lpg=PA168&ots=GBaIDVCCtS&dq=december%2026%2C%201843%20octonion&pg=PA168#v=onepage&q=december%2026,%201843%20octonion&f=false.
^ (Graves 1845년)
^ 1963년, 뉴욕, 존슨 레프린트 주식회사, 수학적 논문집 재인쇄 부록Cayley, Arthur (1845), "On Jacobi's elliptic functions, in reply to the Rev.; and on quaternions", Philosophical Magazine, 26: 208–211, doi:10.1080/14786444508645107, 페이지 127
^ Hamilton (1848), "Note, by Sir W. R. Hamilton, respecting the researches of John T. Graves, Esq.", Transactions of the Royal Irish Academy, 21: 338–341
^ Jump up to: ^a ^b G Gentili; C Stoppato; DC Struppa; F Vlacci (2009), "Recent developments for regular functions of a hypercomplex variable", in Irene Sabadini; M Shapiro; F Sommen (eds.), Hypercomplex analysis, Birkhäuser, p. 168, ISBN 978-3-7643-9892-7
^ L. V. Sabinin; L. Sbitneva; I. P. Shestakov (2006), "§17.2 Octonion algebra and its regular bimodule representation", Non-associative algebra and its applications, CRC Press, p. 235, ISBN 0-8247-2669-3
^ Rafał Abłamowicz; Pertti Lounesto; Josep M. Parra (1996), "§ Four ocotonionic basis numberings", Clifford algebras with numeric and symbolic computations, Birkhäuser, p. 202, ISBN 0-8176-3907-1
^ Jörg Schray; Corinne A. Manogue (January 1996), "Octonionic representations of Clifford algebras and triality", Foundations of Physics, 26 (1): 17–70, arXiv:hep-th/9407179, Bibcode:1996FoPh...26...17S, doi:10.1007/BF02058887, S2CID 119604596. ArXive 사전 인쇄로 사용 가능 그림 1은 여기에 있다.
^ Jump up to: ^a ^b (Baez 2002, 페이지 6)
^ Tevian Dray & Corinne A Manogue (2004), "Chapter 29: Using octonions to describe fundamental particles", in Pertti Lounesto & Rafał Abłamowicz (eds.), Clifford algebras: applications to mathematics, physics, and engineering, Birkhäuser, p. 452, ISBN 0-8176-3525-4 그림 29.1: 투영 평면에 대한 곱셈표 표현
^ (Bauz 2002, 페이지 37–38)
^ (콘웨이 & 스미스 2003, 8.6장)
^ (콘웨이 & 스미스 2003, 8장)
^ 배즈(2002년), 섹션 4.
^ Wilson, Robert A. (2009-09-15). "Octonions and the Leech lattice" (PDF). Journal of Algebra. 322 (6): 2186–2190. doi:10.1016/j.jalgebra.2009.03.021.
^ Wilson, Robert A. (2010-08-13). "Conway's group and octonions" (PDF). Journal of Group Theory. 14: 1–8. doi:10.1515/jgt.2010.038. S2CID 16590883.
^ Günaydin, M.; Gürsey, F. (1973). "Quark structure and octonions". Journal of Mathematical Physics. 14 (11): 1651–1667. doi:10.1063/1.1666240.
Günaydin, M.; Gürsey, F. (1974). "Quark statistics and octonions". Physical Review D. 9 (12): 3387–3391. doi:10.1103/PhysRevD.9.3387.
^ Kugo, Taichiro; Townsend, Paul (1983-07-11). "Supersymmetry and the division algebras". Nuclear Physics B. 221 (2): 357–380. doi:10.1016/0550-3213(83)90584-9.
^ Baez, John C.; Huerta, John (2010). "Division Algebras and Supersymmetry I". In Doran, R.; Friedman, G.; Rosenberg, J. (eds.). Superstrings, Geometry, Topology, and C*-algebras. American Mathematical Society. arXiv:0909.0551.
^ Wolchover, Natalie (2018-07-20). "The Peculiar Math That Could Underlie the Laws of Nature". Quanta Magazine. Retrieved 2018-10-30.
^ Furey, Cohl (2012-07-20). "Unified theory of ideals". Physical Review D. 86 (2): 025024. arXiv:1002.1497. Bibcode:2012PhRvD..86b5024F. doi:10.1103/PhysRevD.86.025024. S2CID 118458623.
Furey, Cohl (2018-10-10). "Three generations, two unbroken gauge symmetries, and one eight-dimensional algebra". Physics Letters B. 785: 84–89. arXiv:1910.08395. Bibcode:2018PhLB..785...84F. doi:10.1016/j.physletb.2018.08.032. S2CID 126205768.
Stoica, O. C. (2018). "Leptons, quarks, and gauge from the complex Clifford algebra $\mathbb {C}$ ℓ₆". Advances in Applied Clifford Algebras. 28: 52. arXiv:1702.04336. doi:10.1007/s00006-018-0869-4. S2CID 125913482.
Gresnigt, Niels G. (2017-11-21). Quantum groups and braid groups as fundamental symmetries. European Physical Society conference on High Energy Physics, 5–12 July 2017, Venice, Italy. arXiv:1711.09011.
Dixon, Geoffrey M. (1994). Division Algebras: Octonions, Quaternions, Complex Numbers and the Algebraic Design of Physics. Springer-Verlag. doi:10.1007/978-1-4757-2315-1. ISBN 978-0-7923-2890-2. OCLC 30399883.
Baez, John C. (2011-01-29). "The Three-Fold Way (Part 4)". The n-Category Café. Retrieved 2018-11-02.
^ Borsten, Leron; Dahanayake, Duminda; Duff, Michael J.; Ebrahim, Hajar; Rubens, Williams (2009). "Black holes, qubits and octonions". Physics Reports. 471 (3–4): 113–219. arXiv:0809.4685. doi:10.1016/j.physrep.2008.11.002. S2CID 118488578.
^ Stacey, Blake C. (2017). "Sporadic SICs and the Normed Division Algebras". Foundations of Physics. 47 (8): 1060–1064. arXiv:1605.01426. Bibcode:2017FoPh...47.1060S. doi:10.1007/s10701-017-0087-2. S2CID 118438232.
^ 진우 등 "손-눈 보정: 4D Procrustes 분석 접근법." 2019년 8월 6일
^ 우, 지아송, 링슈, 푸즈우, 유영콩, 로티 센하드지, 화홍슈. "딥 옥토니언 네트워크" 신경 컴퓨팅(2020년).

참조

Baez, John C. (2002). "The Octonions". Bulletin of the American Mathematical Society. 39 (2): 145–205. arXiv:math/0105155. doi:10.1090/S0273-0979-01-00934-X. ISSN 0273-0979. MR 1886087. S2CID 586512.
Baez, John C. (2005). "Errata for The Octonions" (PDF). Bulletin of the American Mathematical Society. 42 (2): 213–214. doi:10.1090/S0273-0979-05-01052-9.
Conway, John Horton; Smith, Derek A. (2003), On Quaternions and Octonions: Their Geometry, Arithmetic, and Symmetry, A. K. Peters, Ltd., ISBN 1-56881-134-9, Zbl 1098.17001. (검토).
Coxeter, H. S. M. (1946), "Integral Cayley numbers.", Duke Math. J., 13 (4): 561–578, doi:10.1215/s0012-7094-46-01347-6, MR 0019111
Dixon, Geoffrey M. (1994), Division Algebras: Octonions, Quaternions, Complex Numbers and the Algebraic Design of Physics, Kluvwer Academic Publishers, ISBN 0-7923-2890-6
Freudenthal, Hans (1985) [1951], "Oktaven, Ausnahmegruppen und Oktavengeometrie", Geom. Dedicata, 19 (1): 7–63, doi:10.1007/BF00233101, MR 0797151, S2CID 121496094
Graves (1845), "On a Connection between the General Theory of Normal Couples and the Theory of Complete Quadratic Functions of Two Variables", Phil. Mag., 26: 315–320, doi:10.1080/14786444508645136
Kirmse (1924), "Über die Darstellbarkeit natürlicher ganzer Zahlen als Summen von acht Quadraten und über ein mit diesem Problem zusammenhängendes nichtkommutatives und nichtassoziatives Zahlensystem", Ber. Verh. Sächs. Akad. Wiss. Leipzig. Math. Phys. Kl., 76: 63–82
Lahti, Usko (2015), Prof. Corvus Adamas: Luvut ja todistusmenetelmät. Johdanto matematiikan perusteisiin innokkaiden opiskelijoiden seurassa., Helsinki: Books on Demand, ISBN 978-952-318-558-6
Salzmann, Helmut; Betten, Dieter; Grundhöfer, Theo; Hähl, Hermann; Löwen, Rainer; Stroppel, Markus (1995), Compact Projective Planes, With an Introduction to Octonion Geometry, De Gruyter Expositions in Mathematics, Walter de Gruyter, ISBN 3-11-011480-1, ISSN 0938-6572, OCLC 748698685
van der Blij, F. (1961), "History of the octaves.", Simon Stevin, 34: 106–125, MR 0130283

외부 링크

"Cayley numbers", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Wilson, R. A. (2008), Octonions (PDF), Pure Mathematics Seminar notes

[1] 사바디니, 아이린 등 “p 168.” Hypercomplex Analysis, Birkhauser, Basel, 2009, https://books.google.com/books?id=H-5v6pPpyb4C&lpg=PA168&ots=GBaIDVCCtS&dq=december%2026%2C%201843%20octonion&pg=PA168#v=onepage&q=december%2026,%201843%20octonion&f=false.

[2] (Graves 1845년)

[3] 1963년, 뉴욕, 존슨 레프린트 주식회사, 수학적 논문집 재인쇄 부록Cayley, Arthur (1845), "On Jacobi's elliptic functions, in reply to the Rev.; and on quaternions", Philosophical Magazine, 26: 208–211, doi:10.1080/14786444508645107, 페이지 127

[4] Hamilton (1848), "Note, by Sir W. R. Hamilton, respecting the researches of John T. Graves, Esq.", Transactions of the Royal Irish Academy, 21: 338–341

[GSSV-5] Jump up to: ^a ^b G Gentili; C Stoppato; DC Struppa; F Vlacci (2009), "Recent developments for regular functions of a hypercomplex variable", in Irene Sabadini; M Shapiro; F Sommen (eds.), Hypercomplex analysis, Birkhäuser, p. 168, ISBN 978-3-7643-9892-7

[Shestakov-6] L. V. Sabinin; L. Sbitneva; I. P. Shestakov (2006), "§17.2 Octonion algebra and its regular bimodule representation", Non-associative algebra and its applications, CRC Press, p. 235, ISBN 0-8247-2669-3

[Parra-7] Rafał Abłamowicz; Pertti Lounesto; Josep M. Parra (1996), "§ Four ocotonionic basis numberings", Clifford algebras with numeric and symbolic computations, Birkhäuser, p. 202, ISBN 0-8176-3907-1

[Manogue-8] Jörg Schray; Corinne A. Manogue (January 1996), "Octonionic representations of Clifford algebras and triality", Foundations of Physics, 26 (1): 17–70, arXiv:hep-th/9407179, Bibcode:1996FoPh...26...17S, doi:10.1007/BF02058887, S2CID 119604596. ArXive 사전 인쇄로 사용 가능 그림 1은 여기에 있다.

[Baez_2002_loc=p._6-9] Jump up to: ^a ^b (Baez 2002, 페이지 6)

[Lounesto-10] Tevian Dray & Corinne A Manogue (2004), "Chapter 29: Using octonions to describe fundamental particles", in Pertti Lounesto & Rafał Abłamowicz (eds.), Clifford algebras: applications to mathematics, physics, and engineering, Birkhäuser, p. 452, ISBN 0-8176-3525-4 그림 29.1: 투영 평면에 대한 곱셈표 표현

[11] (Bauz 2002, 페이지 37–38)

[12] (콘웨이 & 스미스 2003, 8.6장)

[13] (콘웨이 & 스미스 2003, 8장)

[14] 배즈(2002년), 섹션 4.

[15] Wilson, Robert A. (2009-09-15). "Octonions and the Leech lattice" (PDF). Journal of Algebra. 322 (6): 2186–2190. doi:10.1016/j.jalgebra.2009.03.021.

[16] Wilson, Robert A. (2010-08-13). "Conway's group and octonions" (PDF). Journal of Group Theory. 14: 1–8. doi:10.1515/jgt.2010.038. S2CID 16590883.

[17] Günaydin, M.; Gürsey, F. (1973). "Quark structure and octonions". Journal of Mathematical Physics. 14 (11): 1651–1667. doi:10.1063/1.1666240.
Günaydin, M.; Gürsey, F. (1974). "Quark statistics and octonions". Physical Review D. 9 (12): 3387–3391. doi:10.1103/PhysRevD.9.3387.

[18] Kugo, Taichiro; Townsend, Paul (1983-07-11). "Supersymmetry and the division algebras". Nuclear Physics B. 221 (2): 357–380. doi:10.1016/0550-3213(83)90584-9.

[19] Baez, John C.; Huerta, John (2010). "Division Algebras and Supersymmetry I". In Doran, R.; Friedman, G.; Rosenberg, J. (eds.). Superstrings, Geometry, Topology, and C*-algebras. American Mathematical Society. arXiv:0909.0551.

[wolchover-20] Wolchover, Natalie (2018-07-20). "The Peculiar Math That Could Underlie the Laws of Nature". Quanta Magazine. Retrieved 2018-10-30.

[21] Furey, Cohl (2012-07-20). "Unified theory of ideals". Physical Review D. 86 (2): 025024. arXiv:1002.1497. Bibcode:2012PhRvD..86b5024F. doi:10.1103/PhysRevD.86.025024. S2CID 118458623.
Furey, Cohl (2018-10-10). "Three generations, two unbroken gauge symmetries, and one eight-dimensional algebra". Physics Letters B. 785: 84–89. arXiv:1910.08395. Bibcode:2018PhLB..785...84F. doi:10.1016/j.physletb.2018.08.032. S2CID 126205768.
Stoica, O. C. (2018). "Leptons, quarks, and gauge from the complex Clifford algebra $\mathbb {C}$ ℓ₆". Advances in Applied Clifford Algebras. 28: 52. arXiv:1702.04336. doi:10.1007/s00006-018-0869-4. S2CID 125913482.
Gresnigt, Niels G. (2017-11-21). Quantum groups and braid groups as fundamental symmetries. European Physical Society conference on High Energy Physics, 5–12 July 2017, Venice, Italy. arXiv:1711.09011.
Dixon, Geoffrey M. (1994). Division Algebras: Octonions, Quaternions, Complex Numbers and the Algebraic Design of Physics. Springer-Verlag. doi:10.1007/978-1-4757-2315-1. ISBN 978-0-7923-2890-2. OCLC 30399883.
Baez, John C. (2011-01-29). "The Three-Fold Way (Part 4)". The n-Category Café. Retrieved 2018-11-02.

[22] Borsten, Leron; Dahanayake, Duminda; Duff, Michael J.; Ebrahim, Hajar; Rubens, Williams (2009). "Black holes, qubits and octonions". Physics Reports. 471 (3–4): 113–219. arXiv:0809.4685. doi:10.1016/j.physrep.2008.11.002. S2CID 118488578.

[23] Stacey, Blake C. (2017). "Sporadic SICs and the Normed Division Algebras". Foundations of Physics. 47 (8): 1060–1064. arXiv:1605.01426. Bibcode:2017FoPh...47.1060S. doi:10.1007/s10701-017-0087-2. S2CID 118438232.

[24] 진우 등 "손-눈 보정: 4D Procrustes 분석 접근법." 2019년 8월 6일

[25] 우, 지아송, 링슈, 푸즈우, 유영콩, 로티 센하드지, 화홍슈. "딥 옥토니언 네트워크" 신경 컴퓨팅(2020년).

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

show v t 수 체계
카운트 가능 세트	자연수( $\mathbb {N}$ ${\$ ) 정수( $\mathbb {Z}$ ${\$ $\mathbb {Z}$ ) 합리적인 숫자( $\mathbb {Q}$ ${\$ $\mathbb {Q}$ ) 구성 가능한 숫자 대수적 숫자( $\mathbb {A}$ ${\$ ) 기간 계산 가능한 숫자 산술수 정의 가능한 실수 가우스 정수
구성 알헤브라스	분할 알헤브라스: 실수( $\mathbb {R}$ ${\$ $\mathbb {R}$ ) 복잡한 숫자( $\mathbb {C}$ ${\$ $\mathbb {C}$ ) 쿼터니온( $\mathbb {H}$ ${\$ $\mathbb {H}$ ) 옥토니언( $\mathbb {O}$ ${\$ $\mathbb {O}$ )
분할 종류들	$\mathbb {R}$ ${\$ 초과 $\mathbb {R}$ 분할복수 스플릿쿼터니온 스플릿옥톤 $\mathbb {C}$ 이상 ${\$ 바이콤플렉스 수 바이쿼터니온스 바이오크토니언스
기타 하이퍼 복합체	이중수 이중 쿼터니온 이중 복합수 쌍곡선 쿼터니언 Sedenion( $\mathbb {S}$ ${\$ $\mathbb {S}$ ) 스플릿 바이쿼터니온 멀티콤플렉스 수 기하 대수학 물리적 공간의 대수 스페이스타임 대수
기타유형	기수 연장된 자연수 비이성수 퍼지 수 초현실수 레비시비타 필드 초현실수 초월수 서수 p-adic 번호(p-adic 솔레노이드) 초자연적 수 초현실수
분류 리스트

show 권한통제
일반	통합 권한 파일(독일)
국립도서관	프랑스. (데이터) 미국
기타	주제용어의 면면적용 마이크로소프트 어학 SUDOC(프랑스 1

Search