동차 유리수
Dyadic rational
수학에서 이항 유리수(二 dy理數, )는 분모가 2의 거듭제곱인 분수로 표현할 수 있는 수를 말합니다.예를 들어, 1/2, 3/2, 3/8은 이항 이성분이지만 1/3은 그렇지 않습니다.이 숫자들은 유한한 이진법 표현을 가진 유일한 숫자이기 때문에 컴퓨터 과학에서 중요합니다.다이나믹 논리학자들은 또한 가중치와 척도, 음악적 시간 기호, 그리고 초기 수학 교육에 적용됩니다.그들은 어떤 실수라도 정확하게 근사할 수 있습니다.
임의의 2진법 유리수의 합, 차 또는 곱은 간단한 공식으로 주어진 또 다른 2진법 유리수입니다.그러나 하나의 반지름 유리수를 다른 반지름 유리수로 나누는 것이 항상 반지름 유리수 결과를 낳는 것은 아닙니다.수학적으로, 이것은 정수의 고리와 유리수의 장 사이에 놓여진, 이차원 유리수가 고리를 형성한다는 것을 의미합니다.이 링은 [ ]로 표시할 수 있습니다
고급 수학에서, 쌍대 유리수는 쌍대 솔레노이드, 민코프스키의 물음표 함수, 다우베치스 웨이블릿, 톰슨 군, 프뤼퍼 2군, 초현실수, 융합수의 구성의 중심입니다.이 숫자들은 유리수와 순서 동형입니다. 이 숫자들은 실수뿐만 아니라 2-아딕 숫자의 하위 시스템을 형성하고 2-아딕 숫자의 분수 부분을 나타낼 수 있습니다.역수학에서 수학적 분석을 공식화하기 위해 자연수에서 이차방정식까지의 함수가 사용되었습니다.
적용들
측정중
가중치와 측정의 많은 전통적인 시스템은 반복되는 반의 개념에 기반을 두고 있는데, 이는 단위의 분수를 측정할 때 이디악적인 유리수를 생성합니다.인치는 십진법 세분류를 사용하는 대신 전통적으로 이항승법으로 세분화됩니다.[1]갤런을 반 갤런, 쿼트, 파인트, 컵으로 나누는 관습적인 구분 또한 다이나딕입니다.[2]고대 이집트인들은 분모수가 64개에 이르는 이변이성질체를 측정에 사용했습니다.[3]마찬가지로 인더스 밸리 문명의 무게 시스템은 대부분 반복되는 반올림에 기반을 두고 있습니다. 인류학자 Heather M.-L. Miller는 "반올림은 빔 밸런스가 있는 비교적 간단한 연산이며, 이 시기의 많은 무게 시스템이 이진 시스템을 사용한 이유일 것입니다."[4]라고 말합니다.
컴퓨팅에서
많은 컴퓨터가 직접적으로 조작할 수 있는 분수수의 한 유형으로 컴퓨터 과학의 중심에 자리잡고 있습니다.[5]특히 컴퓨터에서 사용하는 데이터 유형으로서 부동소수점 숫자는 정수에 양 또는 음의 거듭제곱을 곱한 것으로 정의되는 경우가 많습니다.IEEE 부동 소수점 데이터 유형과 같이 부동 소수점 형식으로 정확하게 표현할 수 있는 숫자를 대표 가능한 숫자라고 합니다.대부분의 부동 소수점 표현의 경우, 표현 가능한 숫자는 이항 유리수의 부분집합입니다.[6]대부분의 경우 2의 거듭제곱을 암시적으로 사용하는 고정 소수점 데이터 유형의 경우에도 마찬가지입니다.[7]이중 논리 연산의 단순성 때문에, 그것들은 또한 구간 산술을 사용하는 정확한 실제 컴퓨팅에 사용되며,[8] 계산 가능한 숫자의 일부 이론적 모델의 중심입니다.[9][10][11]
임의의 비트로부터 일정한 시간 동안 임의 변수를 생성하는 것은 변수가 모든 확률이 반동 유리수인 결과를 유한하게 많이 가질 때만 가능합니다.확률이 반동적이지 않은 확률 변수의 경우 반동적 논리로 확률을 근사화하거나 시간 자체가 무작위이고 무한한 무작위 생성 과정을 사용해야 합니다.[12]
음악에서
![{ \new PianoStaff << \new Staff \relative c'' { \set Staff.midiInstrument = #"violin" \clef treble \tempo 8 = 126 \time 3/16 r16 <d c a fis d>\f-! r16\fermata | \time 2/16 r <d c a fis d>-! \time 3/16 r <d c a fis d>8-! | r16 <d c a fis d>8-! | \time 2/8 <d c a fis>16-! <e c bes g>->-![ <cis b aes f>-! <c a fis ees>-!] } \new Staff \relative c { \set Staff.midiInstrument = #"violin" \clef bass \time 3/16 d,16-! <bes'' ees,>-! r\fermata | \time 2/16 <d,, d,>-! <bes'' ees,>-! | \time 3/16 d16-! <ees cis>8-! | r16 <ees cis>8-! | \time 2/8 d16\sf-! <ees cis>-!->[ <d c>-! <d c>-!] } >> }](http://upload.wikimedia.org/score/1/z/1zzwtstcg7ijflwa0wr9fnxe9tbf3yo/1zzwtstc.png)
서양 음악 표기법의 시간 기호는 전통적으로 분수와 비슷한 형태(예: , , 또는 )로 쓰이지만,[13] 상단과 하단 숫자를 구분하는 음악 스태프의 가로줄은 보통 스태프와 따로 쓸 때 생략됩니다.분수로서 그것들은 일반적으로 다이애딕적이지만,[14] 비 다이애딕적 시간 기호도 사용됩니다.[15]분수로 해석되는 서명의 숫자 값은 측정값의 길이를 전체 노트의 분수로 나타냅니다.분자는 측정당 비트 수를 나타내고 분모는 각 비트의 길이를 나타냅니다.[13][14]
수학교육에서
장 피아제(Jean Piaget)의 연구에 기초한 분수 개념의 어린 시절 발달 이론에서, 반과 반복되는 반의 수는 가장 초기 형태의 분수 중 하나입니다.[16]분수의 개념을 발전시키는 이 단계를 "알고리즘 반으로"라고 부릅니다.[17]이러한 숫자의 덧셈과 뺄셈은 정수를 두 배, 반, 더하기, 빼기만 포함하는 단계에서 수행할 수 있습니다.반대로, 더 일반적인 분수의 덧셈과 뺄셈은 공통 분모에 도달하기 위해 정수 곱셈과 인수분해를 포함합니다.따라서 학생들이 일반적인 분수보다 더 쉽게 계산할 수 있습니다.[18]
정의 및 산술
이항수는 정수를 2의 거듭제곱으로 나눈 유리수입니다.[9] [19]q}이가) 2의 거듭제곱일 때 간단히 유리수 은(는) 유리수입니다.이항 유리수를 정의하는 또 다른 동등한 방법은 이들이 종결 이진법을 갖는 실수라는 것입니다.[9]
다음 공식에 따라 임의의 두 이항 유리체의 덧셈, 뺄셈, 곱셈은 또 다른 이항 유리체를 생성합니다.[20]
그러나 하나의 반동적 이성을 다른 반동적 이성으로 나누는 결과가 반드시 반동적 이성이라고 할 수는 없습니다.[21]예를 들어, 1과 3은 모두 진법 유리수이지만, 1/3은 그렇지 않습니다.
추가속성


모든 정수, 그리고 모든 반 정수는 반이수적입니다.[22]둘 다 정수를 2의 거듭제곱으로 나눈 정의를 충족합니다. 모든 정수는 1로 나눈 정수이고(2의 0제곱), 모든 반수는 2로 나눈 정수입니다.
모든 실수는 임의로 진법 이성에 의해 근사될 수 있습니다.특히 실수 의 경우 ⌊ x ⌋ / i{\ 2/2^{i의 논리곱을 고려하십시오 여기서 는 임의의 정수와 ⌊가 될 수 있습니다… ⌋ {\는 인수를 정수로 반올림하는 바닥 함수를 나타냅니다.이 숫자는 에서 1 i {\1의 오차 범위 에서 x {\displaystyle x에 근사합니다 을(를) 임의로 크게 선택하여 임의로 작게 만들 수 있습니다.실수 부분 집합의 경우, 이 오차 한계는 최적의 상수 계수 내에 있습니다. 이 숫자들의 경우, 일정한 횟수 i {\2^{i}보다 작은 오차를 갖는 / i {\ 2^{가 없습니다[23][24]정확한 다이애딕 근사치의 존재는 모든 다이애딕 이성들의 집합이 실제 선에서 밀도가 높다고 말함으로써 표현될 수 있습니다.[22]더욱 강력하게, 분모 가 인 이 집합은 실제 선에서 균일하게 간격을 두고 있다는 점에서 균일하게 밀도가 높습니다.[9]
이변이성계는 정확히 유한한 이진 확장을 가진 수들입니다.[9]이들의 이진 확장은 고유하지 않습니다. 0이 아닌 각 다이애딕 유리체에 대한 유한한 표현과 무한한 표현이 하나 있습니다(단자 0 무시).예를 들어, 0.11 = 0.10111..., 3/4에 대해 두 가지 다른 표현을 제공합니다.이진 확장이 유일하지 않은 유일한 숫자는 이항 유리수입니다.[9]
고급수학에서
대수적 구조
이들은 덧셈, 뺄셈, 곱셈에서는 닫히지만 나눗셈은 아니기 때문에, 이항이성질체는 고리이지만 장이 아닙니다.[26]이중 유리수의 고리는 [ ] 로 나타낼 수 있으며 이는 인수 1/2에서 정수 계수로 다항식을 계산하여 생성할 수 있음을 의미합니다.[27]고리로써, 유리수는 유리수의 부분 고리이고, 정수의 부분 고리입니다.[28]대수학적으로, 이 고리는 2개의 거듭제곱에 대한 정수의 국소화입니다.[29]
진법 유리수는 실수의 부분 고리를 형성할 뿐만 아니라 2진법 숫자의 부분 고리를 형성하는데, 이는 이진점의 오른쪽으로 유한하지만 왼쪽으로 무한히 확장될 수 있는 이진법 표현으로부터 정의될 수 있는 수 체계입니다.2진법의 수는 단지 진법의 수가 아니라 모든 유리수를 포함합니다.2진법 유리수를 포함시키는 것은 2진법 유리수의 산술을 바꾸지 않지만, 그것은 그들이 실수의 하위 고리로서 가지고 있는 것과는 다른 위상 구조를 제공합니다.그들이 실제에서 하는 것과 같이, 이중 유리수는 2-아딕 수의 조밀한 부분 집합을 형성하며,[30] 유한한 이진 확장을 갖는 2-아딕 수의 집합입니다.모든 2-아딕 수는 2-아딕 정수와 2-아딕 유리수의 합으로 분해될 수 있습니다. 이러한 의미에서, 2-아딕 유리수는 2-아딕 수의 분수 부분을 나타낼 수 있지만, 이 분해는 유일하지 않습니다.[31]
정수에 의한 이항체의 이항체 이성분 모듈로 1( Z[/ /\를 더하면 프뤼퍼 2-군이 됩니다.[32]
다이나믹 솔레노이드
이항이성질체의 덧셈과 뺄셈 연산만을 고려하면 가산 아벨 군의 구조가 됩니다.폰트랴긴 이중성(Pontryagin duality)은 점별 곱셈을 이중군 연산으로 하여 원소가 원래 군의 문자인 이중군을 복소수의 곱셈군으로 묶어서 아벨 군을 이해하는 방법입니다.이와 같이 구성된 가산이변이성의 이중군은 위상군으로도 볼 수 있습니다.이는 이 곱에 대각 이성분을 포함함으로써 인용되는 실수와 2진법 수의 위상곱과 동형입니다.[30]그것은 원형, 솔레노이드, 그리고 분해할 수 없는 연속체의 예입니다.[33]
변칙적 유리수를 구별된 점으로 하는 함수
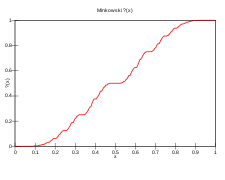
이들은 실수들의 밀집된 부분 집합이기 때문에, 숫자 순서와 함께 이항 유리수들은 밀집된 순서를 형성합니다.칸토어의 동형 정리에 의해 무한히 셀 수 있는 임의의 두 개의 조밀 선형 차수와 마찬가지로,[34] 이중 유리수는 유리수와 동형입니다.이 경우 민코프스키의 물음표 함수는 모든 유리수의 집합과 이항 유리수의 집합 사이의 순서 보존 비투영을 제공합니다.[35]
이러한 웨이블릿의 스케일링 함수가 매끄럽지 못한 점들의 집합으로서, 다이애딕 합리는 다우베치스 웨이블릿의 분석에 핵심적인 역할을 합니다.[26]마찬가지로, 이중 논리는 헤논 지도의 매개 변수 공간에서 안정점과 불안정점 사이의 경계의 불연속성을 매개 변수화합니다.[36]
단위 간격에서 2개의 기울기의 거듭제곱과 반비례 중단점을 갖는 자신까지의 구간별 선형 동형체 집합은 함수 구성 연산 하에 그룹을 형성합니다.이것은 톰슨 그룹으로, 무한하지만 유한하게 제시된 단순한 그룹의 첫번째 알려진 예입니다.[37]동일한 그룹은 루트 이진 트리에 대한 동작 또는 [38]단위 구간 내의 다이애딕 논리에 대한 동작으로 나타낼 수도 있습니다.[32]
역수학에서 실수를 구성하는 한 가지 방법은 실수들을 단수에서 쌍수까지의 함수로 표현하는 것인데, i 에 대한 이러한 함수들 중 하나의 값은 주어진 실수에 근사하는 분모 i 2인 쌍수입니다.이런 식으로 실수를 정의하는 것은 수학적 분석의 많은 기본적인 결과를 "실행 가능한 분석"(BTFA)이라고 불리는 2차 산술의 제한된 이론 안에서 증명할 수 있게 해줍니다.[39]
초현실수는 모든 유한 이변 이성분을 생성하는 것으로 시작하여 무한, 무한소 및 기타 수들의 새롭고 이상한 종류를 생성하는 반복 구성 원리에 의해 생성됩니다.[40]이 수 체계는 조합 게임 이론의 기초가 되며, 이 이론에서 이 수 체계는 특정 조합 게임의 값들의 집합으로서 자연스럽게 발생합니다.[41][42][19]
퓨저블 수는 x ↦(+ y+ )/ + y + 1 / 2 {\displaystyle x,mapsto (x + y + 연산 하에서 집합{ 을(를) -< < 과(를) 쌍으로 제한하는 동적 논리의 부분 집합입니다순서 유형이 엡실론 번호 ε 과(와) 동일한 순서로 정렬되어 각 정수 n {\ n에 대해 n보다 큰 최소 퓨저블 수는 + {\2^{ 형식을 갖습니다각 에 k 의 존재는 Peano 산술에서 증명할 수 없으며 k는 n 의 함수로 매우 빠르게 증가하여 = 3 n=의 경우 (큰 숫자에 대한 Knuth의 상향 arrow 표기법에서) 이미 ↑ 9 보다 큽니다
우리존의 보조정리의 일반적인 증명은 보조정리로부터 분리함수를 구성하기 위해 이항분수를 사용합니다.
참고문헌
- ^ Rudman, Peter S. (2009), How Mathematics Happened: The First 50,000 Years, Prometheus Books, p. 148, ISBN 978-1-61592-176-8
- ^ Barnes, John (2016), Nice Numbers, Springer International Publishing, doi:10.1007/978-3-319-46831-0, ISBN 978-3-319-46830-3,
Note that binary measures (2, 4, 8, 16) are very common indeed. This is particularly obvious with volumes.
- ^ Curtis, Lorenzo J. (1978), "Concept of the exponential law prior to 1900", American Journal of Physics, 46 (9): 896–906, Bibcode:1978AmJPh..46..896C, doi:10.1119/1.11512
- ^ Miller, Heather M.-L. (2013), "Weighty matters: evidence for unity and regional diversity from the Indus civilization weights", in Abraham, Shinu Anna; Gullapalli, Praveena; Raczek, Teresa P.; Rizvi, Uzma Z. (eds.), Connections and Complexity: New Approaches to the Archaeology of South Asia, Left Coast Press, pp. 161–177, doi:10.4324/9781315431857, ISBN 978-1-59874-686-0Miller, Heather M.-L. (2013), "Weighty matters: evidence for unity and regional diversity from the Indus civilization weights", in Abraham, Shinu Anna; Gullapalli, Praveena; Raczek, Teresa P.; Rizvi, Uzma Z. (eds.), Connections and Complexity: New Approaches to the Archaeology of South Asia, Left Coast Press, pp. 161–177, doi:10.4324/9781315431857, ISBN 978-1-59874-686-0특히 페이지 166 참조.
- ^ Resnikoff, Howard L.; Wells, Raymond O. Jr. (1998), "2.2.1: Digital computers and measurement", Wavelet Analysis: The Scalable Structure of Information, New York: Springer-Verlag, pp. 17–18, doi:10.1007/978-1-4612-0593-7, ISBN 0-387-98383-X, MR 1712468
- ^ Kirk, David B.; Hwu, Wen-mei W. (2013), "7.2 Representable numbers", Programming Massively Parallel Processors: A Hands-on Approach (2nd ed.), Morgan Kaufmann, pp. 155–159, ISBN 978-0-12-391418-7
- ^ Kneusel, Ronald T. (2017), "Chapter 6: Fixed-point numbers", Numbers and Computers (2nd ed.), Springer International Publishing, pp. 183–214, doi:10.1007/978-3-319-50508-4_6
- ^ van der Hoeven, Joris (2006), "Computations with effective real numbers", Theoretical Computer Science, 351 (1): 52–60, doi:10.1016/j.tcs.2005.09.060, MR 2201092
- ^ a b c d e f g Ko, Ker-I (1991), Complexity Theory of Real Functions, Progress in Theoretical Computer Science, Boston, Massachusetts: Birkhäuser Boston, Inc., pp. 41–43, doi:10.1007/978-1-4684-6802-1, ISBN 0-8176-3586-6, MR 1137517, S2CID 11758381
- ^ Zheng, Xizhong; Rettinger, Robert (2004), "Weak computability and representation of reals", Mathematical Logic Quarterly, 50 (4–5): 431–442, doi:10.1002/malq.200310110, MR 2090389, S2CID 15815720
- ^ Ambos-Spies, Klaus; Zheng, Xizhong (2019), "On the differences and sums of strongly computably enumerable real numbers", in Manea, Florin; Martin, Barnaby; Paulusma, Daniël; Primiero, Giuseppe (eds.), Computing with Foresight and Industry: 15th Conference on Computability in Europe, CiE 2019, Durham, UK, July 15–19, 2019, Proceedings, Lecture Notes in Computer Science, vol. 11558, Cham: Springer, pp. 310–322, doi:10.1007/978-3-030-22996-2_27, MR 3981892, S2CID 195795492
- ^ Jerrum, Mark R.; Valiant, Leslie G.; Vazirani, Vijay V. (1986), "Random generation of combinatorial structures from a uniform distribution", Theoretical Computer Science, 43 (2–3): 169–188, doi:10.1016/0304-3975(86)90174-X, MR 0855970
- ^ a b Jones, Shelly M.; Pearson, Dunn (May 2013), "Music: highly engaged students connect music to math", General Music Today, 27 (1): 18–23, doi:10.1177/1048371313486478, S2CID 220604326
- ^ a b Libbey, Theodore (2006), "Time signature", The NPR Listener's Encyclopedia of Classical Music, Workman Publishing, p. 873, ISBN 978-0-7611-2072-8
- ^ Yanakiev, Ivan K. (2020), "Mathematical devices in aid of music theory, composition, and performance", in Bozhikova, Milena (ed.), Music between Ontology and Ideology, Cambridge Scholars Publishing, pp. 35–62, ISBN 978-1-5275-4758-2특히 37쪽을 Yanakiev, Ivan K. (2020), "Mathematical devices in aid of music theory, composition, and performance", in Bozhikova, Milena (ed.), Music between Ontology and Ideology, Cambridge Scholars Publishing, pp. 35–62, ISBN 978-1-5275-4758-2보라.
- ^ Hiebert, James; Tonnessen, Lowell H. (November 1978), "Development of the fraction concept in two physical contexts: an exploratory investigation", Journal for Research in Mathematics Education, 9 (5): 374–378, doi:10.2307/748774, JSTOR 748774
- ^ Pothier, Yvonne; Sawada, Daiyo (November 1983), "Partitioning: the emergence of rational number ideas in young children", Journal for Research in Mathematics Education, 14 (5): 307–317, doi:10.2307/748675, JSTOR 748675
- ^ Wells, David Graham (2015), Motivating Mathematics: Engaging Teachers And Engaged Students, World Scientific, pp. 32–33, ISBN 978-1-78326-755-2
- ^ a b Uiterwijk, Jos W. H. M.; Barton, Michael (2015), "New results for Domineering from combinatorial game theory endgame databases", Theoretical Computer Science, 592: 72–86, arXiv:1506.03949, doi:10.1016/j.tcs.2015.05.017, MR 3367582, S2CID 5899577
- ^ 코크 상호작용 정리 속담의 언어로 쓰여진 이들과 동등한 공식들은 다음과 같이 주어집니다.
- ^ O'Connor, Russell (2007), "A monadic, functional implementation of real numbers", Mathematical Structures in Computer Science, 17 (1): 129–159, doi:10.1017/S0960129506005871, MR 2311089, S2CID 221168970
- ^ a b Sabin, Malcolm (2010), Analysis and Design of Univariate Subdivision Schemes, Geometry and Computing, vol. 6, Springer, p. 51, ISBN 9783642136481
- ^ 더 정확하게 말하면, ε 의 작은 양의 값의 경우 일정한 횟수 ε/ 보다 작은 오차를 가진 n/ n/가 없는 실수 집합은 ε 의 함수로서 하우스도르프 차원을 갖는 칸토어 집합을 형성합니다ε \}이가) 0에 가까워지면 1로 이동합니다.그림에는 ε = = {\에 대한 이 세트가 나와 있습니다
- ^ Nilsson, Johan (2009), "On numbers badly approximable by dyadic rationals", Israel Journal of Mathematics, 171: 93–110, doi:10.1007/s11856-009-0042-9, MR 2520103
- ^ Kac, Mark (1959), Statistical Independence in Probability, Analysis and Number Theory, Carus Mathematical Monographs, vol. 12, New York: John Wiley & Sons for the Mathematical Association of America, pp. 2–3, MR 0110114
- ^ a b Pollen, David (1992), "Daubechies' scaling function on [0,3]", Wavelets, Wavelet Analysis and Its Applications, vol. 2, Boston, Massachusetts: Academic Press, pp. 3–13, MR 1161245
- ^ Bajnok, Béla (2013), An Invitation to Abstract Mathematics, Undergraduate Texts in Mathematics, New York: Springer, p. 186, doi:10.1007/978-1-4614-6636-9, ISBN 978-1-4614-6635-2
- ^ 의 서브링과 의 오버링인 링에 대한 Estes 및 Ohm 표기에서 이항체 유리수는 Z{ 입니다 의 섹션 7 참조
- ^ Lucyshyn-Wright, Rory B. B. (2018), "Convex spaces, affine spaces, and commutants for algebraic theories", Applied Categorical Structures, 26 (2): 369–400, arXiv:1603.03351, doi:10.1007/s10485-017-9496-9, MR 3770912, S2CID 3743682
- ^ a b Manners, Freddie (2015), "A solution to the pyjama problem", Inventiones Mathematicae, 202 (1): 239–270, arXiv:1305.1514, Bibcode:2015InMat.202..239M, doi:10.1007/s00222-014-0571-7, MR 3402799, S2CID 119148680섹션 6.2.1 "모델 케이스: [ ] 페이지 255–257을 Manners, Freddie (2015), "A solution to the pyjama problem", Inventiones Mathematicae, 202 (1): 239–270, arXiv:1305.1514, Bibcode:2015InMat.202..239M, doi:10.1007/s00222-014-0571-7, MR 3402799, S2CID 119148680참조하십시오.
- ^ Robert, Alain M. (2000), "5.4 Fractional and integral parts of -adic numbers", A Course in -adic Analysis, Graduate Texts in Mathematics, vol. 198, New York: Springer-Verlag, pp. 40–43, doi:10.1007/978-1-4757-3254-2, ISBN 0-387-98669-3, MR 1760253
- ^ a b de Cornulier, Yves; Guyot, Luc; Pitsch, Wolfgang (2007), "On the isolated points in the space of groups" (PDF), Journal of Algebra, 307 (1): 254–277, arXiv:math/0511714, doi:10.1016/j.jalgebra.2006.02.012, MR 2278053, S2CID 11566447
- ^ Nadler, S. B. Jr. (1973), "The indecomposability of the dyadic solenoid", The American Mathematical Monthly, 80 (6): 677–679, doi:10.2307/2319174, JSTOR 2319174
- ^ Bhattacharjee, Meenaxi; Macpherson, Dugald; Möller, Rögnvaldur G.; Neumann, Peter M. (1997), "Rational numbers", Notes on Infinite Permutation Groups, Texts and Readings in Mathematics, vol. 12, Berlin: Springer-Verlag, pp. 77–86, doi:10.1007/978-93-80250-91-5_9, ISBN 81-85931-13-5, MR 1632579
- ^ Girgensohn, Roland (1996), "Constructing singular functions via Farey fractions", Journal of Mathematical Analysis and Applications, 203 (1): 127–141, doi:10.1006/jmaa.1996.0370, MR 1412484
- ^ Cvitanović, Predrag; Gunaratne, Gemunu H.; Procaccia, Itamar (1988), "Topological and metric properties of Hénon-type strange attractors", Physical Review A, Third Series, 38 (3): 1503–1520, Bibcode:1988PhRvA..38.1503C, doi:10.1103/PhysRevA.38.1503, MR 0970237, PMID 9900529
- ^ Brin, Matthew G. (1999), "The ubiquity of Thompson's group F in groups of piecewise linear homeomorphisms of the unit interval", Journal of the London Mathematical Society, Second Series, 60 (2): 449–460, arXiv:math/9705205, doi:10.1112/S0024610799007905, MR 1724861, S2CID 14490692
- ^ Cannon, J. W.; Floyd, W. J. (2011), "What is … Thompson's group?" (PDF), Notices of the American Mathematical Society, 58 (8): 1112–1113, MR 2856142
- ^ Fernandes, António M.; Ferreira, Fernando (2005), "Basic applications of weak König's lemma in feasible analysis" (PDF), Reverse Mathematics 2001, Lecture Notes in Logic, vol. 21, La Jolla, California: Association for Symbolic Logic, pp. 175–188, MR 2185433
- ^ Conway, J. H. (2001), On Numbers and Games (Second ed.), Natick, Massachusetts: A K Peters, ISBN 1-56881-127-6, MR 1803095 14 1 {\ 등을 참조하십시오.
- ^ Mauldon, J. G. (1978), "Num, a variant of Nim with no first-player win", The American Mathematical Monthly, 85 (7): 575–578, doi:10.2307/2320870, JSTOR 2320870, MR 0503877
- ^ Flanigan, J. A. (1982), "A complete analysis of black-white Hackendot", International Journal of Game Theory, 11 (1): 21–25, doi:10.1007/BF01771244, MR 0665515, S2CID 119964871
- ^ Erickson, Jeff; Nivasch, Gabriel; Xu, Junyan (June 2021), "Fusible numbers and Peano arithmetic", Proceedings of the 36th Annual ACM/IEEE Symposium on Logic in Computer Science (LICS 2021), IEEE, pp. 1–13, arXiv:2003.14342, doi:10.1109/lics52264.2021.9470703, S2CID 214727767
- ^ Sloane, N. J. A. (ed.), "Sequence A188545", The On-Line Encyclopedia of Integer Sequences, OEIS Foundation
| 대수적 구조 → 고리 이론 고리이론 |
|---|
 |
![{\displaystyle \mathbb {Z} [{\tfrac {1}{2}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc0cd93b7492cdaf8d7d38f960b7f12d4d370eb1)



![{\displaystyle {\begin{aligned}{\frac {a}{2^{b}}}+{\frac {c}{2^{d}}}&={\frac {2^{d-\min(b,d)}a+2^{b-\min(b,d)}c}{2^{\max(b,d)}}}\\[6px]{\frac {a}{2^{b}}}-{\frac {c}{2^{d}}}&={\frac {2^{d-\min(b,d)}a-2^{b-\min(b,d)}c}{2^{\max(b,d)}}}\\[6px]{\frac {a}{2^{b}}}\cdot {\frac {c}{2^{d}}}&={\frac {ac}{2^{b+d}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f95f8e3614559dcdc24ac07b56d2e9cb325bb77)


 1
1
 (를) 임의로 크게 선택하여 임의로 작게 만들 수 있습니다.실수
(를) 임의로 크게 선택하여 임의로 작게 만들 수 있습니다.실수 
![{\displaystyle \mathbb {Z} [{\tfrac {1}{2}}]/\mathbb {Z} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/75217251b1b4f3ab9abfe4eb64adcc1a79c02c24)




![{\displaystyle {\widehat {\mathbb {Z} [1/2]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/837dd17d4285f0f6556fa882ceb196b60ab4a25b)







