분할복수

대수에서, 분할 콤플렉스 수(또는 쌍곡수, 복잡한 수, 이중 수)는 두 개의 실수 성분인 x와 y를 가지며, 여기서² z = x + y j로 표기된다. z의 결합은 z^∗ = x - y j. j = 1이므로², 그 결합을 가진 숫자 z의 곱은 zz^∗2 = x - y², 등방성 2차 형태, N(z) = x² - y이다².

모든 분할 콤플렉스 숫자의 집합 D = x = x + y j, y ∈ R은 실수의 영역에 걸쳐 대수학을 형성한다. w와 z의 두 분할 복합 번호는 N(wz) = N(w)N(z)을 만족하는 제품 wz를 가지고 있다. 대수 곱에 대한 N의 이러한 구성은 (D, +, ×, *) 합성 대수(composition 대수)를 만든다.

R과² 덧셈과 곱셈의 성분별 연산을 바탕으로 한 유사한 대수학(R², +, ×, xy) 여기서 xy는 R의² 2차 형태인 2차 공간도 형성한다. 반지 이형성

${\displaystyle {\reasoned}D&\\to \mathb {R} ^{2}\\x+yj&\mapsto (x-y,x+y)\ended{arged}}}$

비례 2차 형태와 관련되지만, R의² 승법정체(1, 1)가 D에서 정규화된 0에서 distance2 거리에 있기 때문에 매핑은 등측도가 아니다.

분할 복합 번호는 다른 많은 이름을 가지고 있다. 아래의 § 동의어를 참조한다. 분할 복합 숫자의 함수는 기사 모터 변수를 참조하십시오.

정의

분할 복합 번호는 순서가 지정된 실수 쌍으로, 양식으로 작성된다.

${\displaystyle z=x+properties}$

여기서 x와 y는 실수이고 j는 수량을 만족한다.

${\displaystyle j^{2}=+1}$

$j{\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$=${\displaystyle }$- ${\displaystyle 1}$ ${\displaystyle$ j$^{2}=-1}$을 선택하면 복잡한 숫자가 나타난다$$. 이것은 일반적인 복잡한 숫자와 분할 복합 수를 구별하는 신호 변화다. 여기의 수량 j는 실수가 아니라 독립수량이다.

그러한 모든 z의 컬렉션을 분할 복합 평면이라고 한다. 분할 복합 숫자의 추가 및 곱셈은 다음에 의해 정의된다.

${\displaystyle {\displaystyle}(x+jv)+(u+jv)&=(x+jv)\\(x+jv)&=(u+jv)+j(xv+yv)+j(xv+yu)).\end{정렬}}}$

이 곱셈은 교감적이고 연관성이 있으며 덧셈에 따라 분포한다.

결합형, 계량형, 이선형

복잡한 숫자와 마찬가지로, 분할 복합 결합의 개념을 정의할 수 있다. 만약

${\displaystyle z=x+properties}$

z의 결합은 다음과 같이 정의된다.

${\displaystyle z^{*}=x-message.}$

이 결합은 일반적인 복잡한 결합과 유사한 성질을 만족시킨다. 즉,

${\displaystyle {\signed}(z+w)^{*}&=z^{*}+w^{*}\\\(zw)^{*}&=z^{***}\\\w(z^{*}\rift)^{*}&=z.\end{정렬}}}$

이 세 가지 특성은 분할 복합 결합이 순서 2의 자동 형태임을 암시한다.

분할 복합 수 z = x + j y의 계수는 등방성 2차 형태에 의해 주어진다.

${\displaystyle \lVert z\rVert =z^{*}=z^{*}z=x^{2}-y^{2}.}$

구성 대수 특성을 가지고 있다.

${\displaystyle \lVert zw\rVert =\lVert z\rVert \lVert w\rVert .}$

그러나 이 이차형식은 양위형식이 아니라 서명(1, -1)을 가지고 있기 때문에 계수가 규범이 아니다.

관련 이선형 형식은 다음에 의해 제공된다.

${\displaystyle \langle z,w\\angle =\operatorname {Re} \좌측(zw^{*}\우측)=\operatorname {Re} \좌측(z^{*}w\우측)=192-yv,}$

여기서 z = x + j y 및 w = u + j v. 계수에 대한 또 다른 표현은 다음과 같다.

${\displaystyle \lVert z\rVert =\langle z,z\angle .}$

이린형은 양립성이 없기 때문에 내향성 제품이 아니며, 그럼에도 불구하고 이린성형은 무기한 내향성 제품이라고 자주 언급된다. 비슷한 언어 남용은 규범으로서 계율을 말한다.

분할 복합 번호는 그 계수가 0이 아닌 경우에만(vert${\displaystyle z}$ ${\displaystyle \Vert }$ ${\displaystyle \ne }$ ${\displaystyle 0}$ {\$displaystyle \lVert z\rbert \neq 0}),$ 따라서 x ± j x는 역이 없다. 반전성 원소의 승법 역은 다음과 같다.

${\displaystyle z^{-1}={\frac {z^{*}}{{\lVert z\rVert }^{2}}.}$

변환할 수 없는 분할 복합 숫자를 null 벡터라고 한다. 이것들은 모두 일부 실수 a에 대한 형태(a ± j a)이다.

대각선 기준

e = (1 - j)/2와 e^∗ = (1 + j)/2로 주어지는 두 개의 비종교적 특이점 요소가 있다. idempotent는 ee = e 및 ee^∗∗ = e를^∗ 의미한다는 것을 상기하라. 이 두 가지 요소는 모두 null:

${\displaystyle \lVert e\rVert =\lVert e^{*}\rVert = e^{*}e=0.}$

분할 복합 평면의 대체 기준으로 e와 e를^∗ 사용하는 것이 종종 편리하다. 이 기준을 대각선 기준 또는 무효 기준이라고 한다. 분할 복합 번호 z는 null 기준으로 다음과 같이 작성할 수 있다.

${\displaystyle z=x+jy=(x-y)e+(x+y)e^{*}.}$

실제 숫자 a와 b에 대해 z = ae + be를^∗ (a, b)로 나타낸다면, split-complex 곱셈은 다음에 의해 주어진다.

${\displaystyle \left(a_{1},b_{1}\오른쪽)\left(a_{2},b_{2}\right)=\left(a_{1}a_{1}a_{2},b_{1}b_{2}}}\right)\right.}$

이 근거에서, 분할 복합 번호는 덧셈과 곱셈을 쌍으로 정의한 직합 R ⊕ R에 대해 링 이형성이라는 것이 명확해진다.

대각선 기준의 분할 복합 결합은 다음과 같이 주어진다.

${\displaystyle (a,b)^{*}=(b,a)}$

그리고 에 의한 계량

${\displaystyle \lVert (a,b)\rVert =ab.}$

고리 범주에서 동일한 이형성 등급에 놓여 있지만, 분할 복합 평면과 두 실제 선의 직접 합은 데카르트 평면의 레이아웃에 차이가 있다. 이형성(異形性)은 평면 지도로서 시계 반대 방향 회전( counter線)을 45°, 확장( dil2)을 √2로 구성한다. 특히 팽창은 때때로 쌍곡선 부분의 영역과 관련하여 혼란을 야기시켰다. 실제로 쌍곡선은 {(a, b) ∈ R : ab = 1}이(가) 제공한 "단위 원"으로 R ⊕ R 면의 섹터 면적에 해당한다. 분할 복합 평면의 수축된 단위 하이퍼볼라 {cosh a + j sinh a : ∈ R}은 해당 쌍곡선 섹터의 범위에 있는 면적의 절반만 가지고 있다. 분할 복합 평면의 지오메트리가 R ⊕ R의 지오메트리와 구별되지 않을 때 그러한 혼란이 영구화될 수 있다.

기하학

민코프스키 내제품이 있는 2차원 리얼 벡터 공간을 (1 + 1)차원 민코프스키 공간이라고 하며, 흔히 R로^1,1 표기한다. 유클리드 평면 R의² 기하학의 많은 부분을 복잡한 숫자로 설명할 수 있듯이, 민코프스키 평면 R의^1,1 기하학은 분할 복합 숫자로 설명할 수 있다.

점 집합

${\displaystyle \left\{z:\lVert z\rVert =a^{2}\right\}}}$

R에서 0이 아닌 모든 것에 대한 하이퍼볼라 입니다. 하이퍼볼라는 (a, 0)과 (-a, 0)를 통과하는 오른쪽과 왼쪽 가지로 구성되어 있다. 사례 a = 1은 단위 하이퍼볼라라고 불린다. 공극 하이퍼볼라는 다음에 의해 주어진다.

${\displaystyle \left\{z:\lVert z\rVert =-a^{2}\right\}}}$

(0, a)와 (0, -a)를 통과하는 상부와 하부의 가지. 하이퍼볼라와 결합 하이퍼볼라는 null 원소의 집합을 형성하는 두 개의 대각선 점근으로 구분된다.

${\displaystyle \left\{z:\lVert z\rVert =0\right\}.}$

이 두 선(때로는 null con이라고도 함)은² R에서 수직이며 기울기는 ±1이다.

분할 복합수 z와 w는 ⟨z, w⟩ = 0일 경우 쌍곡직교라고 한다. 특히 일반적인 복잡한 수 산술에서 알려진 바와 같이, 일반적인 정형성과 유사하지만, 이 조건은 더욱 미묘하다. 그것은 스페이스타임에 동시 하이퍼플레인 개념의 기초를 형성한다.

분할 복합 숫자에 대한 오일러의 공식의 아날로그는

$[\displaystyle \exp(j\theta )=\cosh(\theta )+j\sinh(\theta )\,}$

이것은 cosh가 고른 힘만 가지고 있는 반면 sinh는 괴상한 힘을 가지고 있다는 사실을 이용한 파워 시리즈 확장에서 파생될 수 있다. 쌍곡선의 모든 실제 값 values에 대해 분할 복합수 λ = exp(jθ)은 규범 1을 가지며, 단위 하이퍼볼라의 오른쪽 가지에 놓여 있다. λ과 같은 숫자는 쌍곡선 버시버라고 불려왔다.

λ은 계수 1을 가지기 때문에, 어떤 분할 복합수 z를 곱하면 z의 계수를 보존하고 쌍곡선 회전을 나타낸다(로렌츠 부스트 또는 압착 매핑이라고도 함). λ에 곱하면 기하학적 구조가 보존되며, 하이퍼볼라를 자기 자신에게, 널 콘을 자기 자신에게 가져간다.

계수를 보존하는 분할 복합 평면의 모든 변환 집합(또는 동등하게 내부 제품)은 일반직교 그룹 O(1, 1)라는 그룹을 형성한다. 이 그룹은 SO⁺(1, 1)로 표시된 부분군을 형성하는 쌍곡선 회전과 4개의 이산 반사로 구성된다.

${\displaystyle z}$ ${\displaystyle \mapsto }$± ${\displaystyle z}$ ${\displaystyle$ z$\mapsto \pm z}$ 및$$ $z{\displaystyle }$ ${\displaystyle \mapsto }$± ${\displaystyle {}^{}}$ $∗.$ {\$displaystyle$ z$\mapsto \pm$ z$^{*}.$$}$

지수 지도

${\displaystyle \exp \colon(\mathb {R},+)\to \mathrm {SO} ^{+}(1,1)}$

exp(jθ)에 의한 회전으로 θ을 보내는 것은 일반적인 지수 공식이 적용되기 때문에 집단 이형성이다.

${\displaystyle e^{j(\theta +\phi )}=e^{j\theta }e^{j\phi }\,}$

분할 복합 숫자 z가 대각선 중 하나에 놓여 있지 않으면, z는 극 분해된다.

대수적 특성

추상 대수학 용어에서, 분할 복합 숫자는 다항식² x - 1에 의해 생성된 이상에 의해 다항식 링 R[x]의 몫으로 설명될 수 있다.

R[x]/(x² - 1)

지수에서 x의 이미지는 "상상적" 단위 j이다. 이 설명으로, 분할 복합 숫자는 실제 숫자에 대한 역대수를 형성한다는 것은 분명하다. null 원소들은 되돌릴 수 없기 때문에 대수학은 필드가 아니다. 0이 아닌 모든 null 요소는 0 divisor이다.

분할복소수는 그 자체로 R의 직접생산에 대한 대수로서 이형성이다. 그래서 축소된 아르티니아 반지다.

덧셈과 곱셈은 평면의 일반적인 위상에 관한 연속적인 연산이기 때문에 분할 복합 수는 위상학적 고리를 형성한다.

분할복소수의 대수는 그 이후 구성대수를 형성한다.

${\displaystyle \Vert }$ z w ${\displaystyle \Vert }$ =${\displaystyle \Vert }$ ${\displaystyle z}$ ${\displaystyle \Vert }$ ${\displaystyle w}$ w {\$displaystyle \lVert zw\rVert =\lVert$ z$\rVert \lVert w\rVert }.$ 모든 숫자 z$$ 및 w.

정의에서 보면, 분할복소수의 링이 실제 숫자 R에 걸쳐 순환군 C의₂ 그룹 링 R[C₂]에 이형성이 있음을 알 수 있다.

행렬 표현

행렬에 따라 분할 복합 숫자를 쉽게 나타낼 수 있다. 분할 복합 수

${\displaystyle z=x+properties}$

행렬로 나타낼 수 있다.

${\displaystyle z\mapsto {\pmatrix}x&y\y&x\end{pmatrix}.}$

분할 복합 숫자의 덧셈과 곱셈은 매트릭스 덧셈과 곱셈에 의해 주어진다. z의 계수는 해당 행렬의 결정 인수에 의해 주어진다. 이 표현에서 분할 복합적 결합은 양쪽에 행렬을 곱하는 것에 해당한다.

${\displaystyle C={\begin{pmatrix}1&0\\0&#1\end{pmatrix}.}$

실제 숫자 a의 경우 쌍곡선 각도에 의한 쌍곡선 회전 a는 행렬에 의한 곱셈에 해당한다.

${\displaystyle {\pmatrix}\cosh a&\sinh a\\\sinh a&\cosh a&\nd{pmatrix}.}$

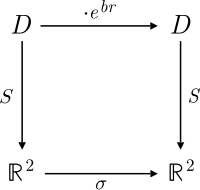
분할 복합 수면에 대한 대각선 기준은 $z{\displaystyle }$= ${\displaystyle x}$+ j ${\displaystyle y}$에 대해 순서가 지정된 쌍($x,$ y$)$을 사용하고 매핑을 수행하여 호출할 수 있다$.$

${\displaystyle (u,v)=(x,y){\begin{pmatrix}1&1\\1&-1\end{pmatrix}=(x,y)S.}$

현재 2차 형태는 ${\displaystyle u}$ v${\displaystyle }$=${\displaystyle }$( ${\displaystyle x}$+ y${\displaystyle }$)${\displaystyle }$= ${\displaystyle {x\mathrm{}}^{}}$ ${\displaystyle {}^{}}$- ${\displaystyle {y\mathrm{}}^{}}$ ${\displaystyle 2{}^{}}$. ${\displaystyle ub=(x+y)(x-y)=x^{2}-y^{2}.$ 더 나아가$$,

${\displaystyle(\cosh a,\sinh a){pmatrix}1&1\\1&-1-1\end{pmatrix}}=\왼쪽(e^{a},e^{-a}\오른쪽)}$

그래서 파라메트리된 두 개의 하이퍼볼라가 S와 통신하게 된다.

쌍곡선 versor $e{\displaystyle {}^{}}$ ${\displaystyle b^{}}$ j $displaystyle$ e$^{bj}\!$그러면 $}$이(가) 이 선형 변환에 따라 스퀴즈 매핑에 해당됨

${\displaystyle \ \ma :(u,v)\mapsto \left(ru,{\frac {v}{r}\right),\map r=e^{b}.}$

2×2 실제 행렬에는 분할 복합 수치의 다양한 표현이 있다. 사실, 정사각형이 정체성 매트릭스인 모든 매트리스는 그러한 표현을 한다.

위의 대각선 표현은 분할 복합 번호의 행렬 표현에 대한 요르단 표준 형식을 나타낸다. 분할 복합 숫자 z = (x, y)가 다음 행렬 표현에 의해 주어지는 경우

${\displaystyle Z={\begin{pmatrix}x&y\y&x\end{pmatrix}}$

요르단의 표준 형식은 다음과 같다.

${\displaystyle J_{z}={\begin{pmatrix}x+y&0\\0&x-y\end{pmatrix},}$

여기서 $Z{\displaystyle }$= ${\displaystyle S}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}{}^{}}$ S${\displaystyle {}^{}}$- ${\displaystyle 1^{}}$,${\$디스플레이 $스타일$ Z$=$$SJ_$${z}S^{-1}\ ,}$ 및

${\displaystyle S={\begin{pmatrix}1&-1\\1&1\end{pmatrix}.}$

역사

분할 콤플렉스 숫자의 사용은 제임스 코클이 테사린을 공개한 1848년으로 거슬러 올라간다.^[1] 윌리엄 킹돈 클리퍼드는 스핀의 합계를 나타내기 위해 분할 복합 숫자를 사용했다. 클리포드는 현재 분할-비쿼터니온이라고 불리는 쿼터니온 대수에서 계수로 분할 복합수를 사용했다고 소개했다. 그는 그것의 요소들을 "모터"라고 불렀는데, 이것은 원 그룹에서 가져간 보통의 복잡한 숫자의 "로터" 작용과 병행하는 용어다. 일반적인 복합 변수의 기능과 대조되는 모터 변수의 기능을 유추한다.

20세기 후반 이후, 분할 복합 곱셈은 보통 시간 평면의 로렌츠 부스트로 보여졌다.^{[2][3][4][5][6][7]} 이 모델에서, 숫자 z = x + y j는 스파시오-임시 평면에서 이벤트를 나타내며, 여기서 x는 나노초 단위로, y는 머민의 발에서 측정된다. 미래는 분할 복합 극지방 분해 $z{\displaystyle }$= ${\displaystyle \rho }$ ${\displaystyle {}^{}}$ e = ${\displaystyle e^{}}$ e j $displaystyle z=\rho$ e$^{aj}\!}$ 사건의 사분면에 해당한다$.$ 모델은 신속도 a의 참조 프레임을 입력하고 by나노초를 기다리면 원점에서 z에 도달할 수 있다고 말한다. 분할 복합 방정식

${\displaystyle e^{b}\ e^{b}=e^{(a+b)j}}}$

하이퍼볼라 단위에서 제품을 표현하는 것은 공선 속도에 대한 속도의 부가성을 보여준다. 사건의 동시성은 신속성 a에 달려 있다.

$\displaystyle \lbrace z=\sigma je^{aj:\sigma \in \mathb {R} \rbrace }}$

빠른 속도 a를 가진 기준 프레임의 원점과 동시에 발생하는 사건의 선입니다.

두 사건^∗ z와 w는 zw + zw^∗ = 0일 때 쌍곡직교로 된다. 표준 사건 exp(aj)와 j exp(aj)는 쌍곡직교로 원점과 동시에 발생한 사건이 j exp(aj)에 비례하는 기준 프레임의 축에 놓여 있다.

1933년에 막스 조른은 분할옥톤을 사용하고 있었고 구성 대수 특성을 주목했다. 그는 분할 알헤브라를 생성하기 위해 사용되는 케이리-딕슨 건설이 분할 옥토온을 포함한 다른 구성 알헤브라를 생성하기 위해 (인자 감마(인자 감마)로 수정될 수 있다는 것을 깨달았다. 그의 혁신은 Adrian Albert, Richard D에 의해 영속되었다. 셰퍼, 그리고 다른 사람들.^[8] 감마 인수는 Ⅱ를 베이스 필드로 하여 합성 대수로서 분할 복합 숫자를 구축한다. 수학 리뷰를 위해 알버트 H. 맥코이를 검토하면서, N. H. McCoy는 "케이리-딕슨 알헤브라를 일반화하는 F보다 순서^e 2의 몇몇 새로운 알헤브라의 도입"^[9]이 있었다고 썼다. F = ℝ, e = 1을 취하는 것은 이 글의 대수학에 해당한다.

1935년 J.C. 비뇨와 A. 두라뇨나 이 비디아(스페인어)는 라플라타 국립대학(라 플라타) 아르헨티나 레부블리카(스페인어)의 레푸블리카스 피시카스 이 마테마티카스 에 있는 4개 기사에서 분할 복합 기하 대수학 및 함수 이론을 발전시켰다. 이 해설서와 교육학상의 논술은 그 주제를 폭넓은 감상의 대상으로 제시하였다.^[10]

1941년 E.F. 앨런은 zz^∗ = 1로 새겨진 삼각형의 9점 하이퍼볼라를 설정하기 위해 분할 복합 기하학적 산수를 사용했다.^[11]

1956년 Mieczyslaw Warmus는 Bulletin de l'Academie polonise des science (참고문헌 링크 참조)에 "근사설의 미적분"을 발표하였다. 그는 두 개의 대수 체계를 개발했는데, 그 각각을 "대략적인 숫자"라고 불렀고, 그 중 두 번째는 진짜 대수학을 형성한다.^[12] D. H. 레머는 수학 리뷰의 기사를 검토하고 이 두 번째 시스템이 이 글의 주제인 "하이퍼볼릭 콤플렉스" 숫자에 이형성이 있다고 관찰했다.

1961년 워머스는 대략적인 숫자의 구성 요소들을 가리켜 표시된 구간의 중간점과 반지름으로 언급하면서 그의 설명을 계속했다.

동의어

다른 작가들은 분할복제 숫자에 매우 다양한 이름을 사용해 왔다. 이 중 일부는 다음과 같다.

• (진짜) 테사린, 제임스 코클 (1848)
• (알지브레이크) 모터, W.K. 클리퍼드(1882)
• 쌍곡 복합수, J.C. 비뇨(1935년)
• 비레알 숫자, U. 벤시벤가 (1946)
• 구간 분석에 사용하기 위한 대략적인 수, Warmus(1956)
• Musean uppernumer의 역복제 또는 쌍곡수.
• 이중 번호, I.M. 야글롬(1968년), 칸토르와 솔로도브니코프(1989년), 헤이즈윙켈(1990년), 루니(2014년)
• 아놀 복합수, W. 벤츠(1973)
• 복잡한 숫자, P. Fjelstad(1986)와 Poodiack & LeClair(2009)
• 로렌츠 숫자, F.R. 하비 (1990)
• 쌍곡수, G. Sobczyk(1995)
• 파라콤플렉스 숫자, Cruceanu, Fortuny & Gadea(1996)
• 반복수, F. 안토누치오(1994년)
• 분할 이진, K. McCrimon(2004)
• 분할 복합 숫자, B. 로젠펠트 (1997년)^[13]
• 스페이스타임 숫자, N. 보로타(2000)
• 연구 번호, P. Lounesto(2001)
• 2중 숫자, S. 올라리우(2002)

분할 콤플렉스 숫자와 그들의 고차원적 친족(분할 쿼터/분할 쿼터 및 분할 옥토니언)은 찰스 무세스가 개발한 하이퍼 넘버 프로그램의 하위 집합이기 때문에 때때로 "무산 수"라고 불렸다.

참고 항목

• 민코스키 공간
• 스플릿쿼터니온
• 하이퍼복합수

참조

위키북 연합 구성 대수학에는 다음과 같은 주제의 페이지가 있다: 분할 이진법

• 벤시벤가, 울드리코 (1946) "술라 라프레센타지오네 기하학아 델레 알헤르 도티 도티 도티 도티 도티 디 모둘로", 아티 델라 레알레 아카드혈증 델레 스키엔제 에 벨레테 디 나폴리, 세르(3) v.2 No.7". MR002123.
• 월터 벤츠 (1973) 보레성겐 우버 기하오메트리 데어 알헤브렌, 스프링거
• N. A. Borota, E. Flores, T. J. Osler(2000), "스팩타임 숫자가 쉬운 방법", 수학 및 컴퓨터 교육 34: 159–168.
• N. A. Borota와 T. J. Osler(2002) "스팩타임 변수의 기능", 수학 및 컴퓨터 교육 36: 231–239.
• K. Carmody, (1988) "순환 및 쌍곡 쿼터니온, 옥톤, 진정제", Appl. 수학, 계산. 28:47–72.
• K. Carmody, (1997) "순환 및 쌍곡선 쿼터니온, 옥톤 및 진정제 - 추가 결과", Appl. 수학, 계산. 84:27–48.
• 윌리엄 킹돈 클리포드 (1882) 수학 작품, A. W. 터커 편집장 392페이지 "바이쿼터니온에 관한 더 많은 노트"
• 브뤼세아누, P. Fortuny & P.M. Gadea(1996) Paracomplex Geometry에 대한 조사, Rocky Mountain Journal of Mathematics 26(1): 83–115 프로젝트 유클리드 링크.
• 미국 물리학 저널 55(4):296, "An은 복잡한 숫자의 목록으로도 알려져 있다."
• 앤서니 A. 하킨 & 조셉 B. 하킨(2004) 일반화 복합수 기하학, 수학잡지 77(2):118–29.
• F. 리스 하비 스피너 및 보정. 샌디에이고의 아카데미 출판사 1990. ISBN 0-12-329650-1. 로렌츠 숫자를 포함하여 무기한 서명의 정규 알헤브라에 대한 설명을 포함한다.
• Hazewinkle, M. (1994) "이중과 이중의 숫자" 수학 백과사전, 소련/AMS/Kluwer, Dordret.
• 케빈 맥크림몬(2004) 조던 알헤브라의 맛, 페이지 66, 157, 유니버시티텍스트, 스프링거 ISBN 0-387-95447-3 MR2014924
• C. Musés, "응용된 하이퍼 배관: 계산 개념", Appl. 수학. 계산 3 (1977) 211–226.
• C. Muses, "Hypernumber II—추가 개념 및 계산 응용 프로그램", Appl. 수학. 계산 4 (1978) 45–66.
• Olariu, Silviu(2002) N차원의 복합수, 1장: 2차원의 쌍곡 복합수, 1-16페이지, North-Holland 수학 연구 #190, Exvier ISBN 0-444-5123-7.
• 푸디악, 로버트 D. & Kevin J. LeClair(2009) "난감한 사람들을 위한 대수학의 근본적 이론", The College Mathical Journal 40(5:322–35).
• Isaak Yaglom (1968) 기하학의 복잡한 번호들, 1963년 러시아 오리지널 학술 출판부, 페이지 18-20에서 E. Primrose가 번역했다.
• J. Rooney (2014). "Generalised Complex Numbers in Mechanics". In Marco Ceccarelli and Victor A. Glazunov (ed.). Advances on Theory and Practice of Robots and Manipulators: Proceedings of Romansy 2014 XX CISM-IFToMM Symposium on Theory and Practice of Robots and Manipulators. Mechanisms and Machine Science. Vol. 22. Springer. pp. 55–62. doi:10.1007/978-3-319-07058-2_7. ISBN 978-3-319-07058-2.