입방체
Cuboid기하학에서, 입방체는 육면체, 6면체의 입체이다.그것의 얼굴은 사변형이다.입방체는 모서리의 길이 또는 모서리와 면 사이의 각도를 조정함으로써 입방체로 변환할 수 있다는 점에서 "입방체와 같다"는 뜻이다.수학에서 입방체는 볼록한 다면체이며, 다면체 그래프는 입방체와 같다.
6개의 정사각형을 면으로 한 큐브, 직사각형 프리즘, 직사각형 입방체 또는 직사각형 상자, 6개의 직사각형을 면으로 한 큐브와 직사각형 프리즘 모두 인접한 면들이 [1][2]직각으로 만나는 것이 특별한 경우이다.
일반 입방체
오일러 공식에 따르면 볼록 다면체의 면 수 F, 정점 V, 모서리 E는 F + V = E + 2 공식으로 관련된다.입방체의 경우 6 + 8 = 12 + 2가 됩니다. 즉, 입방체와 마찬가지로 입방체는 면 6개, 정점 8개, 모서리 12개를 가집니다.직사각형의 입방체와 함께, 모든 평행입방체는 정사각형의 정점 절단에 의해 형성된 정사각형과 같은 유형의 입방체이다.
| 사변면 육면체(입방체) 면 6개, 모서리 12개, 정점 8개 | ||||||
|---|---|---|---|---|---|---|
 |  |  |  |  | 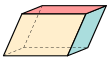 | 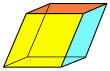 |
| 큐브 (사각형) | 직사각형 입방체 (3쌍의 직사각형) | 삼각삼면체 (동일 마름모) | 삼각삼면체 (일치 사변수) | 사각형 좌골 (스위치 변경) 정사각형 피라미드) | 평행관 (3쌍의 평행사변형) | 마름모꼴 (3쌍의 마름모꼴) |
| Oh, [4,3], (*432) 오더48 | D2h, [2,2], (*222) 오더 8 | D3d, [2+,6], (2*3) 주문 12 | D3, [2,3]+, (223) 오더 6 | C4v, [4], (*44) 오더 8 | Ci, [2+,2+], (×) 주문 2 | |
직사각형 입방체
| 직사각형 입방체 | |
|---|---|
 | |
| 유형 | 프리즘 사면체 |
| 얼굴 | 6개의 직사각형 |
| 가장자리 | 12 |
| 꼭지점 | 8 |
| 대칭군 | D2h, [2,2], (*222), 순서 8 |
| 슐레플리 기호 | { } × { } × { } |
| 콕서터 다이어그램 | |
| 이중 다면체 | 직사각형 융기 |
| 특성. | 볼록, 조노면체, 등교 |
직사각형 입방체에서는 모든 각도가 직각이며 입방체의 마주보는 면은 같다.정의상 이것은 직각 프리즘으로 하며, 직각 평행입방체 또는 직교 평행입방체라는 용어도 이 다면체를 나타내기 위해 사용된다.그러나 "직사각 프리즘"과 "오블롱 프리즘"이라는 용어는 모든 각도를 규정하지 않기 때문에 모호하다.
정사각형, 정사각형 상자 또는 오른쪽 정사각형 프리즘(모호한 표현으로 정사각형 프리즘이라고도 함)은 적어도 두 개의 면이 정사각형인 정사각형의 특수한 경우입니다.이것은 슐레플리 기호 {4} × {}을(를) 가지며 대칭은 [2,2]에서 [4,2], 차수 16으로 두 배가 됩니다.
입방체는 6개의 면 모두가 정사각형인 정사각형 입방체의 특별한 경우이다.이 기호는 슐레플리 기호 {4,3}이며 대칭이 [2,2]에서 [4,3], 차수 48로 향상되었습니다.
직사각형 입방체의 치수가 a, b, c이면 부피는 abc이고 표면적은 2(ab + ac + bc)이다.
대각선의 길이는
상자, 찬장, 방, 건물, 컨테이너, 캐비닛, 책, 튼튼한 컴퓨터 섀시, 인쇄 장치, 전자 호출 터치 스크린 장치, 세탁기 및 건조기 등에 큐보이드 모양이 자주 사용됩니다.입방체는 3차원 공간을 테셀링할 수 있는 고체 중 하나입니다.이 모양은 상자 안의 각설탕, 찬장의 상자, 방의 찬장, 건물의 방 등 여러 개의 작은 큐보이드를 담을 수 있는 꽤 다재다능합니다.
정수 면 대각선뿐만 아니라 정수 모서리를 가진 입방체를 예를 들어 변 44, 117 및 240을 가진 오일러 벽돌이라고 합니다.완벽한 입방체는 공간 대각선이 정수인 오일러 벽돌이다.완벽한 입방체가 실제로 존재하는지 여부는 현재 알려져 있지 않다.
네츠
단순한 큐브의 다른 그물 수는 11개입니다.그러나 길이가 [3]3개인 직사각형 입방체의 경우 이 숫자는 54로 크게 증가합니다.
「 」를 참조해 주세요.
레퍼런스
- ^ Robertson, Stewart Alexander (1984). Polytopes and Symmetry. Cambridge University Press. p. 75. ISBN 9780521277396.
- ^ Dupuis, Nathan Fellowes (1893). Elements of Synthetic Solid Geometry. Macmillan. p. 53. Retrieved December 1, 2018.
- ^ Steward, Don (May 24, 2013). "nets of a cuboid". Retrieved December 1, 2018.
외부 링크
- Weisstein, Eric W. "Cuboid". MathWorld.
- 직사각형 프리즘 및 큐보이드 종이 모형 및 그림



