비트런드 큐빅 벌집

비트런드 큐빅 벌집

유형	균일 벌집
슐레플리 기호	2t{4,3,4} t_1,2{4,3,4}
콕시터-딘킨 도표
세포형	(4.6.6)
면 종류	정사각형 {4} 육각형 {6}
에지 피겨	등각 삼각형 {3}
정점수	(사각형 분산형)
스페이스 그룹 피브리폴트 표기법 콕시터 표기법	임3m (229) 8^o:2 [[4,3,4]]
콕시터군	${\tilde {C}}_{3}$ ~ ${\tilde {C}}_{3}$ ${\$ [4,3,4]
이중	테트라헤드릴 주 디스페노이드 사면체 벌집 셀:
특성.	이소곤, 동위원소, 이소콜리아

여기에 표시된 입방체 벌집형 벌집형 벌집형 벌집형입니다.

잘린 입방체 벌집은 잘린 옥타헤드라(또는 동등하게 잘린 정육면체)로 구성된 유클리드 3공간의 공간을 채우는 테셀레이션(또는 벌집)이다. 각 꼭지점 주위에 4개의 잘린 옥타헤드라가 있다. 전체적으로 잘린 옥타헤드라로 구성되는 것은 세포 전이적이다. 또한 가장자리 변환이며, 각 가장자리에는 2개의 육각과 1개의 정사각형이 있으며, 정점 변환이다. 그것은 28개의 균일한 벌집중 하나이다.

존 호튼 콘웨이(John Horton Conway)는 이 벌집을 그의 건축가 및 강직 테셀레이션 리스트에서 잘린 옥타헤드릴(Octavedrille)이라고 부르는데, 이 벌집은 디스페노이드 사면 벌집이라고도 한다. 일반 사면체만으로는 공간을 테셀레이팅할 수 없지만, 이 이중은 삼각형 면과 동일한 분산형 사면체 세포를 가지고 있다.

기하학

보로노이 테셀레이션(Boronoi tesceleration)으로 체중 중심의 큐빅 격자(cubic lattice)를 실현시킬 수 있다. 켈빈 경은 약간 깎인 입방 벌집(얼굴과 가장자리는 곡선이 있지만 결합 구조는 동일함)의 변종이 최적의 비누 거품 거품이라고 추측했다. 그러나, 대칭성이 떨어지는 많은 구조물들은 나중에 비눗방울의 더 효율적인 거품인 것으로 밝혀졌는데, 그 중에서 Weaire---펠란 구조는 최고로 보인다.

벌집합은 3공간의 순면체 테셀레이션을 나타낸다. 한 옥타헤드론에 대한 정점의 좌표는 (1,2,3,4)의 순열인 4-공간 정수의 하이퍼플레인이다. 테셀레이션은 하이퍼플레인 내에서 번역된 복사본으로 형성된다.

테셀레이션은 3-공간에서 평행선 테셀레이션이 가장 높은 것이다.

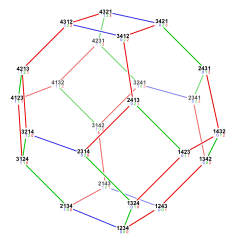
투영

박리된 입방체 벌집합은 다양한 대칭 배열로 유클리드 평면에 직교 투영될 수 있다. 가장 높은 (헥스각형) 대칭은 균일하지 않은 림프트리헥스각형 타일링으로 투영된다. 정사각형 대칭 투영법은 겹치는 두 개의 잘린 정사각형 타일링을 형성하며, 모따기 정사각형 타일링으로 결합된다.

직교 투영
대칭	p6m(*632)	p4m(*442)	pmm(*2222)
고체
틀

대칭

${\tilde {A}}_{3}$ 벌집의 꼭지점은 분산형 사면체이며, A ${\tilde {A}}_{3}$ ~ 3 ${\$ 콕세터 ${\tilde {A}}_{3}$ 그룹의 구르사트 사면체(근본적 영역)이기도 하다. 이 벌집에는 네 개의 균일한 구조물이 있는데 잘린 팔면체 세포는 서로 다른 Coxeter 그룹과 Wythoff 구조를 가지고 있다. 이러한 균일한 대칭은 각 구조에서 세포의 색상을 다르게 하여 나타낼 수 있다.

셀별 5가지 균일한 색상
스페이스 그룹	임3m (229)	Pm3m(221개)	Fm3m(225)	F43m(216)	Fd3m(227)
피브리폴드	8^o:2	4⁻:2	2⁻:2	1^o:2	2⁺:2
콕시터군	${\tilde {C}}_{3}$ ~ ${\tilde {C}}_{3}$ ${\$ ${\tilde {C}}_{3}$ 2 [[4,3,4]] =[4[3^[4]]] =	${\tilde{C}_{3}$ [4,3,4] =[2[3^[4]]] =	${\tilde{B}_{3}$ [4,3^1,1] =<[3^[4]]> =	${\tilde{A}_{3}$ [3^[4]]	${\tilde {A}}_{3}$ ~ ${\tilde {A}}_{3}$ ${\$ ${\tilde {A}}_{3}$ 2 [[3^[4]]] =[[3^[4]]]
콕시터 다이어그램
잘린 옥타헤드라	1	1:1 :	2:1:1 ::	1:1:1:1 :::	1:1 :
정점수
꼭지점 형상을 나타내다 대칭	[2⁺,4] (주문 8)	[2] (주문 4)	[ ] (주문 2)	[ ]⁺ (주문 1)	[2]⁺ (주문 2)
이미지 색칠자 세포를 놓다

관련 다면체 및 허니컴

일반 꼬치 아페이로헤드론 {6,4 4}에는 이 벌집의 육각형이 들어 있다.

[4,3,4], , Coxeter 그룹은 15개의 균일한 테셀레이션 순열을 생성하며, 9는 대체 큐빅 벌집합을 포함한 뚜렷한 형상을 가지고 있다. 확장된 큐빅 벌집(런케이트된 큐빅 벌집이라고도 함)은 큐빅 벌집과 기하학적으로 동일하다.

C3 허니컴
공간 무리를 짓다	피브리폴드	확장됨 대칭	확장됨 도표를 만들다	주문	허니컴스
Pm3m (221)	4⁻:2	[4,3,4]		×1	₁, ₂, ₃, ₄, ₅, ₆
Fm3m (225)	2⁻:2	[1⁺,4,3,4] ↔ [4,3^1,1]	↔	절반	₇, ₁₁, ₁₂, ₁₃
I43m (217)	4^o:2	[[(4,3,4,2⁺)]]		하프 × 2	₍₇₎,
Fd3m (227)	2⁺:2	[[1⁺,4,3,4,1⁺]] ↔ [[3^[4]]]	↔	쿼터 × 2	₁₀,
임3m (229)	8^o:2	[[4,3,4]]		×2	₍₁₎, ₈, ₉

[4,3^1,1], , Coxeter 그룹은 9개의 균일한 테셀레이션 순열을 생성하며, 4는 대체 큐빅 벌집합을 포함한 뚜렷한 기하학적 구조를 가지고 있다.

B3 허니컴
공간 무리를 짓다	피브리폴드	확장됨 대칭	확장됨 도표를 만들다	주문	허니컴스
Fm3m (225)	2⁻:2	[4,3^1,1] ↔ [4,3,4,1⁺]	↔	×1	₁, ₂, ₃, ₄
Fm3m (225)	2⁻:2	<[1⁺,4,3^1,1]> ↔ <[3^[4]]>	↔	×2	₍₁₎, ₍₃₎
Pm3m (221)	4⁻:2	<[4,3^1,1]>		×2	₅, ₆, ₇, ₍₆₎, ₉, ₁₀, ₁₁

이 ${\tilde {A}}_{3}$ 은 ${\tilde {A}}_{3}$ ~ ${\tilde {A}}_{3}$ 3 {\ $displaystyle {\tilde{A}_{$ 3}} Coxeter ${\tilde {A}}_{3}$ 그룹에 의해 구성된 5개의 뚜렷한 균일한 벌집합^[1] 중 하나이다. 대칭은 Coxeter-Dynkin 다이어그램에서 링의 대칭으로 곱할 수 있다.

A3 허니컴
공간 무리를 짓다	피브리폴드	사각형 대칭	확장됨 대칭	확장됨 도표를 만들다	확장됨 무리를 짓다	허니콤 도표
F43m (216)	1^o:2	a1	[3^[4]]		${\tilde{A}_{3}$	(없음)
Fm3m (225)	2⁻:2	d2	<[3^[4]]> ↔ [4,3^1,1]	↔	${\tilde {A}}_{3}$ ~ ${\tilde {A}}_{3}$ ${\$ ${\tilde {A}}_{3}$ 2₁ £ ${\tilde {B}}_{3}$ ~ ${\$ {\ $tild{B}_{3}}}$	₁, ₂
Fd3m (227)	2⁺:2	g2	[[3^[4]]] 또는 [2⁺[3^[4]]	↔	${\tilde {A}}_{3}$ ~ ${\tilde {A}}_{3}$ ${\$ ${\tilde {A}}_{3}$ 2₂	₃
Pm3m (221)	4⁻:2	d4	<2[3^[4]]> ↔ [4,3,4]	↔	${\tilde {A}}_{3}$ ~ ${\tilde {A}}_{3}$ ${\$ ${\tilde {A}}_{3}$ 4₁ 파운드 ${\tilde {C}}_{3}$ ~ ${\tilde {C}}_{3}$ ${\$	₄
I3 (204)	8^−o	r8	[4[3^[4]]]⁺ ↔ [[4,3⁺,4]]	↔	½ ${\tilde {A}}_{3}$ ~ ${\tilde {A}}_{3}$ ${\$ 8 파운드 ${\tilde {C}}_{3}$ ~ ${\tilde {C}}_{3}$ ${\$ ${\tilde {C}}_{3}$ 2	_(*)
임3m (229)	8^o:2	r8	[4[3^[4]]] ↔ [[4,3,4]]	↔	${\tilde {A}}_{3}$ ~ ${\tilde {A}}_{3}$ ${\$ ×8 파운드 ${\tilde {C}}_{3}$ ~ ${\tilde {C}}_{3}$ ${\$ ${\tilde {C}}_{3}$ 2	₅

대체형식

교번 비트롤드 큐빅 벌집
유형	볼록스 벌집
슐레플리 기호	2s{4,3,4} 2s{4,3^1,1} sr{3^[4]}
콕시터 도표	= = =
세포	사면체 이코사헤드론
정점수
콕시터군	[[4⁺,3,4 ${\tilde {C}}_{3}$ ${\tilde {C}}_{3}$ ~ 3 ${\$
이중	10대 다이몬드 벌집 셀:
특성.	정점 변환의

이 벌집은 교대로 만들어질 수 있으며, 틈새에 생긴 분산형 사면세포로 잘린 옥타면체로부터 화농성 이코사면체를 만들 수 있다. 관련된 3개의 Coxeter-Dynkin 도표로부터 , , , , , , 등 3개의 구조물이 있다. 이것들은 각각 [4,3,4⁺], [4^1,1, (3)], ⁺[3]⁺의^[4] 대칭을 가지고 있다. 첫 번째와 마지막 대칭은 [4,3⁺,4]와 [3]로^[4] ⁺곱할 수 있다.

이중 벌집은 직경 10개 디카헤드라라고 불리는 세포로 만들어진다.

5개의 균일한 컬러링
스페이스 그룹	I3(204)	Pm3(200)	Fm3(202)	Fd3(203)	F23(196)
피브리폴드	8^−o	4⁻	2⁻	2^o+	1^o
콕시터군	[[4,3⁺,4]]	[4,3⁺,4]	[4,(3^1,1)⁺]	[[3^[4]]]⁺	[3^[4]]⁺
콕시터 다이어그램
주문	곱절로 하다	가득 찬	절반	4분의 1 곱절로 하다	4분의 1
이미지 세포로 색칠한

이 벌집은 α-롬비헤드랄 결정의 붕소 원자에 표현되어 있다. 이코사헤드라의 중심은 격자의 FCC 위치에 있다.^[2]

참고 항목

메모들

^ [1], A000029 6-1건, 0 표시가 있는 1건 건너뛰기
^ 윌리엄스, 1979년, 페이지 199, 그림 5-38.

참조

존 H. 콘웨이, 하이디 버기엘, 차임 굿맨 스트라우스(2008) 사물의 대칭성, ISBN978-1-56881-220-5 (21장, 아르키메데스 및 카탈루냐 다면체 및 기울기 이름 지정, 건축가 및 강직 테셀레이션, 페이지 292-298은 모든 비자유적 형식을 포함한다)
조지 올셰프스키, 균일 파노플로이드 테트라콤브스, 원고(2006) (11개의 볼록 균일 기울기, 28개의 볼록 균일 벌집, 143개의 볼록 균일 테트라콤 목록)
브란코 그룬바움, 3공간의 균일한 기울기. Gembinatorics 4(1994), 49 - 56.
케일리디스코어: H.S.M. Coxeter의 선별된 글, F가 편집한 글. 아서 셔크, 피터 맥멀런, 앤서니 C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [2]
- (용지 22) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 I, [산술] Zeit. 46 (1940) 380-407, MR 2,10](1.9 균일한 공간 채우기)
A. 안드레이니, 술레 레티디 리골라리 e 세미레골라리 e 설레 코리스폰덴티 레티 상관관계(폴리헤드라의 정규망과 반정형 그물 및 그에 상응하는 상관 그물 위에), 멤. 소시에타 이탈리아아 델라 시엔제, 세르.3, 14 (1905) 75–129.
Klitzing, Richard. "3D Euclidean Honeycombs o4x3x4o - batch - O16".
3-스페이스의 균일한 허니컴: 05-배치
Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X.

외부 링크

Weisstein, Eric W. "Space-filling polyhedron". MathWorld.

[1] [1], A000029 6-1건, 0 표시가 있는 1건 건너뛰기

[2] 윌리엄스, 1979년, 페이지 199, 그림 5-38.

[1]

[2]

Search

비트런드 큐빅 벌집

네임스페이스

더

목차

기하학

투영

대칭

관련 다면체 및 허니컴

대체형식

관련 폴리토페스

참고 항목

메모들

참조

외부 링크