과대산출 임계값
Percolation threshold이 글은 대부분의 독자들이 이해하기에는 너무 기술적인 것일 수도 있다.할 수 하십시오2021년 3월)(이 및 |
퍼콜레이션 임계값은 무작위 시스템에서 장거리 연결의 형성을 기술하는 퍼콜레이션 이론의 수학 개념이다. 한계치 아래에는 거대하게 연결된 구성요소가 존재하지 않으며, 그 위에 있는 동안 시스템 크기 순서의 거대한 구성요소가 존재한다. 공학과 커피 제조에서, 퍼콜레이션은 다공성 매체를 통한 유체의 흐름을 나타내지만, 수학 및 물리학 세계에서는 일반적으로 무작위 시스템이나 네트워크(그래프)의 단순화된 격자 모델과 그 안에 있는 연결성의 성격을 가리킨다. 과집합 임계값은 직업 확률 p의 임계 값 또는 보다 일반적으로 매개변수 p1, p2, ...의 그룹에 대한 임계 표면으로서 무한 연결(과집합)이 먼저 발생한다.
퍼콜레이션 모델
가장 일반적인 퍼콜레이션 모델은 사각 격자처럼 규칙적인 격자를 취하여 무작위로 "점용" 사이트(수직) 또는 통계적으로 독립적인 확률 p를 가진 결합(에지)을 통해 무작위 네트워크로 만드는 것이다. 임계 임계값 p에서는c 먼저 큰 클러스터와 장거리 연결이 나타나며 이를 퍼콜레이션 임계값이라고 한다. 무작위 네트워크를 얻는 방법에 따라 사이트 과집 임계값과 결합 과집 임계값을 구별한다. 보다 일반적인 시스템은 몇 가지 확률2 p1, p 등을 가지며, 전환은 임계 표면이나 다지관으로 특징지어진다. 무작위로 배치된 디스크와 구를 겹치는 것과 같은 연속체 시스템이나 음의 공간(스위스-치즈 모델)도 고려할 수 있다.
지금까지 기술된 제도에서는 부지나 채권의 점유는 완전히 무작위라고 가정되어 왔다. 이것이 이른바 베르누이 퍼콜레이션이다. 연속체 시스템의 경우, 무작위 점유는 포아송 공정에서 배치되는 점들에 해당한다. 추가 변동은 Fortuin-Kastleyn 방법에 의해 결합이 내려지는 페로마네트의 Ising 및 Potts 모델과 관련된 퍼콜레이션 클러스터와 같은 상관된 퍼콜레이션을 포함한다.[1] 부트스트랩 또는 k-sat 퍼콜에서 사이트 및/또는 결합은 먼저 점유된 다음 사이트에 적어도 k개의 이웃이 없는 경우 시스템에서 연속적으로 도태된다. 다른 보편성 클래스에서 전체적으로 다른 중요한 퍼콜레이션의 또 다른 중요한 모델은 퍼콜레이션 방향이며, 여기서 결합을 따르는 연결성은 흐름의 방향에 따라 달라진다.
지난 수십 년 동안, 이러한 다양한 시스템에 대한 정확하고 대략적인 퍼콜레이션 임계값의 값을 찾기 위해 엄청난 양의 작업이 진행되었다. 정확한 임계값은 삼각형 변환에서 시스템이 그대로 유지되도록 자체 이중 배열로 분할할 수 있는 특정 2차원 격자에 대해서만 알려져 있다. 수치적 방법을 이용한 연구는 알고리즘의 수많은 개선과 몇 가지 이론적 발견으로 이어졌다.
단순히 2차원의 이중성은 모든 완전 삼각형 격자(예: 삼각형, 유니언 잭, 크로스 듀얼, 마티니 듀얼 및 아사노하 또는 3-12 듀얼, 델라우나이 삼각측량)가 모두 부지 임계값이 1/2이고 자가 이중 격자(제곱, 마티니-B)가 1/2임을 의미한다.
(4,82)와 같은 표기법은 그룬바움(Grünbaum)과 셰퍼드(Shephard)에서 유래하며,[2] 주어진 꼭지점 주위에서 시계방향으로 가다가 정사각형 주위로 한 사람이 먼저 마주치고 그 다음에 두 옥타곤을 만난다는 것을 나타낸다. 모든 부지가 동일한 일반 폴리곤으로 구성된 11개의 아르키메데스 격자 외에도, 다른 등급의 부지가 있는 더 복잡한 격자들도 연구되어 왔다.
마지막 자리 또는 숫자의 오류 막대는 괄호 안의 숫자로 표시된다. 따라서 0.729724(3)는 0.729724 ± 0.000003을 의미하며, 0.74042195(80)는 0.74042195 ± 0.00000080을 의미한다. 오차 막대는 출처에 따라 순오차(통계적 및 예상 계통적 오차 포함)의 표준 편차 또는 경험적 신뢰 구간을 다양하게 나타낸다.
2D 격자에서의 퍼콜레이션
아르키메데스 격자의 임계값
이것은 11개의 아르키메데스 래티스 또는 균일 기울기를 그린 그림으로[3], 모든 폴리곤이 규칙적이고 각 꼭지점이 동일한 폴리곤의 순서로 둘러싸여 있다. 예를 들어 "(3, 64)"이라는 표기법은 모든 꼭지점이 4개의 삼각형과 1개의 육각형으로 둘러싸여 있다는 것을 의미한다. 이러한 격자에 부여된 몇 가지 일반적인 이름이 아래 표에 나열되어 있다.
| 격자 | z | 사이트 과집 임계값 | 본드 퍼콜레이션 임계값 | |
|---|---|---|---|---|
| 3-12 또는 (3, 122 ) | 3 | 3 | 0.807900764... = (1 - 2개 죄(π/18)1/2[4] | 0.74042195(80),[5] 0.74042077(2)[6] 0.740420800(2),[7] 0.7404207988509(8),[8][9] 0.740420798850811610(2),[10] |
| 교차, 잘린 3헥사형(4, 6, 12) | 3 | 3 | 0.746,[11] 0.750,[12] 0.747806(4),[4] 0.7478008(2)[8] | 0.6937314(1),[8] 0.69373383(72),[5] 0.693733124922(2)[10] |
| 사각 팔각형, 욕실 타일, 4-8, 잘린 사각형 (4, 82) | 3 | - | 0.729,[11] 0.729724(3),[4] 0.7297232(5)[8] | 0.6768,[13] 0.67680232(63),[5] |
| 벌집(63) | 3 | 3 | 0.6962(6),[14] 0.697040230(5),[8] 0.6970402(1),[15] 0.6970413(10),[16] 0.697043(3),[4] | 0.652703645... = 1-2 죄(π/18), 1+p-3p32=0[17] |
| 카고메 (3, 6, 3, 6) | 4 | 4 | 0.652703645... = 1 - 2개 죄(π/18)[17] | 0.5244053(3),[18] 0.52440516(10),[16] 0.52440499(2),[15] 0.524404978(5),[6] 0.52440572...,[19] 0.52440500(1),[7] 0.524404999173(3),[8][9] 0.524404999167439(4)[20] 0.52440499916744820(1)[10] |
| 루비,[21] Rhombitrihexangle(3, 4, 6, 4) | 4 | 4 | 0.620,[11] 0.621819(3),[4] 0.62181207(7)[8] | 0.52483258(53),[5] 0.5248311(1),[8] 0.524831461573(1)[10] |
| 정사각형4(4) | 4 | 4 | 0.59274(10),[22] 0.59274605079210(2),[20] 0.59274601(2),[8] 0.59274605095(15),[23] 0.59274621(13),[24] 0.59274621(33),[25] 0.59274598(4),[26][27] 0.59274605(3),[15] 0.593(1),[28] 0.591(1),[29] 0.569(13),[30] 0.59274(5)[31] | 1/2 |
| 육각형, 단풍잎[32](34,6) | 5 | 5 | 0.579[12] 0.579498(3)[4] | 0.43430621(50),[5] 0.43432764(3),[8] 0.4343283172240(6),[10] |
| 사각형, 퍼즐(32, 4, 3, 4 ) | 5 | 5 | 0.550,[11][33] 0.550806(3)[4] | 0.41413743(46),[5] 0.4141378476(7),[8] 0.4141378565917(1),[10] |
| 프리제, 긴3 삼각형(3, 42) | 5 | 5 | 0.549,[11] 0.550213(3),[4] 0.5502(8)[34] | 0.4196(6),[34] 0.41964191(43),[5] 0.41964044(1),[8] 0.41964035886369(2) [10] |
| 삼각형(36) | 6 | 6 | 1/2 | 0.347296355... = 2개의 죄(π/18), 1 + p - 3p3[17] = 0 |
참고: 벌집형 대신 "헥스각형"을 사용하기도 하지만, 일부 분야에서는 삼각 격자라고도 한다. z = 벌크 조정 번호.
확장되고 복잡한 이웃이 있는 2D 선반
이 절에서 sq-1,2,3은 제곱(NN+2NN+3N)[35] 등에 해당한다. 제곱-2N+3N+4N,[36] sq(1,2,3)에 해당한다.[37] tri = 삼각형, hc = 벌집형.
| 격자 | z | 사이트 과집 임계값 | 본드 퍼콜레이션 임계값 |
|---|---|---|---|
| sq-1, sq-2, sq-3, sq-5 | 4 | 0.5927...[35][36] (제곱 사이트) | |
| sq-1,2, sq-2,3, sq-3, sq-3,5 | 8 | 0.407...[35][36][38] (제곱 일치) | 0.25036834(6),[15] 0.2503685,[39] 0.25036840(4) [40] |
| sq-1,3 | 8 | 0.337[35][36] | 0.2214995[39] |
| sq-2,5: 2NN+5NN | 8 | 0.337[36] | |
| hc-1,2,3: 벌집-NN+2N+3NN | 12 | 0.300[37] | |
| tri-1,2: 삼각-NN+2NN | 12 | 0.295,[37] 0.289,[12] | |
| tri-2,3: 삼각-2N+3NN | 12 | 0.232020(36),[41] | |
| sq-4: 제곱-4NN | 8 | 0.270...[36] | |
| sq-1,5: 제곱-NN+5NN | 8(r ≤ 2) | 0.277[36] | |
| sq-1,2,3: 제곱-NN+2N+3NN | 12 | 0.292,[42] 0.290(5) [43] 0.289,[12] 0.288,[35][36] | 0.1522203[39] |
| sq-2,3,5: 제곱-2N+3N+5N+5NN | 12 | 0.288[36] | |
| sq-1,4: 제곱-NN+4NN | 12 | 0.236[36] | |
| sq-2,4: 제곱-2N+4NN | 12 | 0.225[36] | |
| 3-4: 삼각-4NN | 12 | 0.192450(36)[41] | |
| tri-1,2,3: 삼각-NN+2N+3NN | 18 | 0.225,[42] 0.215,[12] 0.215459(36)[41] | |
| sq-3,4: 3NN+4N | 12 | 0.221[36] | |
| sq-1,2,5: NN+2N+5NN | 12 | 0.240[36] | 0.13805374[39] |
| sq-1,3,5: NN+3N+5NN | 12 | 0.233[36] | |
| sq-4,5: 4NN+5NN | 12 | 0.199[36] | |
| sq-1,2,4: NN+2N+4NN | 16 | 0.219[36] | |
| sq-1,3,4: NN+3N+4NN | 16 | 0.208[36] | |
| sq-2,3,4: 2N+3N+4NN | 16 | 0.202[36] | |
| sq-1,4,5: NN+4N+5NN | 16 | 0.187[36] | |
| sq-2,4,5: 2N+4N+5N+5N | 16 | 0.182[36] | |
| sq-3,4,5: 3N+4N+5N+5N | 16 | 0.179[36] | |
| sq-1,2,3,5: NN+2N+3NN+5N | 16 | 0.208[36] | 0.1032177[39] |
| 3-4,5: 4N+5N | 18 | 0.140250(36),[41] | |
| sq-1,2,3,4: NN+2N+3N+4NN (r≤ | 20 | 0.196[36] 0.196724(10)[44] | 0.0841509[39] |
| sq-1,2,4,5: NN+2N+4NN+5N | 20 | 0.177[36] | |
| sq-1,3,4,5: NN+3N+4NN+5N | 20 | 0.172[36] | |
| sq-2,3,4,5: 2N+3N+4NN+5N | 20 | 0.167[36] | |
| sq-1,2,3,5,6: NN+2N+3NN+5N+6NN | 20 | 0.0783110[39] | |
| sq-1,2,3,4,5: NN+2N+3N+4NN+5NN (≤ 8 | 24 | 0.164[36] | |
| tri-1,4,5: NN+4N+5NN | 24 | 0.131660(36)[41] | |
| sq-1,...,6: NN+...+6NN(r≤3) | 28 | 0.142[12] | 0.0558493[39] |
| tri-2,3,4,5: 2N+3N+4NN+5N | 30 | 0.117460(36)[41] | |
| tri-1,2,3,4,5: NN+2N+3N+4NN+5N | 36 | 0.115,[12] 0.115740(36)[41] | |
| sq-1,...,7: NN+...+7NN(r≤ | 36 | 0.113[12] | 0.04169608[39] |
| 제곱: 제곱 거리 ≤ 4 | 40 | 0.105(5)[43] | |
| sq-(1,..., 8: NN+..+8NN (r≤ | 44 | 0.095765(5),[44] 0.095[33] | |
| sq-1,...,9: NN+..+9NN | 48 | 0.086 [12] | 0.02974268[39] |
| sq-1,...,11: NN+...+11NN | 60 | 0.02301190(3)[39] | |
| sq-1,... (r ≤ 7) | 148 | 0.008342595[40] | |
| sq-1,...,32: NN+...+32NN | 224 | 0.0053050415(33)[39] | |
| sq-1,...,86: NN+...+86NN(r≤15) | 708 | 0.001557644(4)[45] | |
| sq-1,...,141: NN+...+141NN (r≤ | 1224 | 0.000880188(90)[39] | |
| sq-1,...,185: NN+...+185NN(r≤23) | 1652 | 0.000645458(4)[45] | |
| sq-1,...,317: NN+...+317NN(r≤31) | 3000 | 0.000349601(3)[45] | |
| sq-1,...,413: NN+...+413NN(r≤ | 4016 | 0.0002594722(11)[39] | |
| 제곱: 제곱 거리 ≤ 6 | 84 | 0.049(5)[43] | |
| 제곱: 제곱 거리 ≤ 8 | 144 | 0.028(5)[43] | |
| 제곱: 제곱 거리 ≤ 10 | 220 | 0.019(5)[43] | |
| 2x2 겹치는 제곱* | 0.58365(2) [44] | ||
| 3x3 겹치는 제곱* | 0.59586(2) [44] |
여기서 NN = 가장 가까운 이웃, 2NN = 두 번째로 가까운 이웃(또는 가장 가까운 이웃), 3NN = 세 번째로 가까운 이웃(또는 다음으로 가까운 이웃) 등 일부 논문에서는 이를 각각 2N, 3N, 4N이라고도 한다.[35]
- 겹치는 정사각형의 여기에 p c{\사이트)는 연속적으로 c _{c와 유사한 를 점유한 사이트의 순 부분이다. The case of a 2×2 system is equivalent to percolation of a square lattice NN+2NN+3NN+4NN or sq-1,2,3,4 with threshold with .[44] The 3×3 system corresponds to sq-1,2,3,4,5,6,7,8 with z=44 and . For larger overlapping squares, see.[44]
아르키메데스 래티스의 임계값에 대한 대략적인 공식
| 격자 | z | 사이트 과집 임계값 | 본드 퍼콜레이션 임계값 |
|---|---|---|---|
| (3, 122 ) | 3 | ||
| (4, 6, 12) | 3 | ||
| (4, 82) | 3 | 0.676835..., 4p3 + 3p4 - 6p5 - 2p6[46] = 1 | |
| 벌집(63) | 3 | ||
| 카고메 (3, 6, 3, 6) | 4 | 0.524430..., 3p2 + 6p3 - 12p4+ 6p56[47] - 1 | |
| (3, 4, 6, 4) | 4 | ||
| 정사각형4(4) | 4 | 1/2 (계속) | |
| (34,6 ) | 5 | 0.434371..., 12p3 + 36p4 - 21p5 - 327p6 + 69p7 + 2532p8 - 6533p9 + 8256p10 - 6255p11 + 2951p12 - 837p13 + 126p14 - 7p15[citation needed] = 1 | |
| 사각형, 퍼즐(32, 4, 3, 4 ) | 5 | ||
| (33, 42) | 5 | ||
| 삼각형(36) | 6 | 1/2 (계속) |
사이트 본드 2D 퍼콜레이션
사이트 본드 퍼콜레이션. 여기서 는 부지 점유 확률이고 p 는 채권 점유 확률이며, 한 경로를 따라 부지와 채권이 모두 점유된 경우에만 연결이 이루어진다. 임계 조건은 곡선 s, ) = 0이 되며, 일부 특정 임계 쌍 , p ) 이 아래에 나열되어 있다.
사각 격자:
| 격자 | z | 사이트 과집 임계값 | 본드 퍼콜레이션 임계값 | |
|---|---|---|---|---|
| 정사각형의 | 4 | 4 | 0.615185(15)[48] | 0.95 |
| 0.667280(15)[48] | 0.85 | |||
| 0.732100(15)[48] | 0.75 | |||
| 0.75 | 0.726195(15)[48] | |||
| 0.815560(15)[48] | 0.65 | |||
| 0.85 | 0.615810(30)[48] | |||
| 0.95 | 0.533620(15)[48] |
벌집형(헥스각형) 격자:
| 격자 | z | 사이트 과집 임계값 | 본드 퍼콜레이션 임계값 | |
|---|---|---|---|---|
| 벌집 모양의 | 3 | 3 | 0.7275(5)[49] | 0.95 |
| 0. 0.7610(5)[49] | 0.90 | |||
| 0.7986(5)[49] | 0.85 | |||
| 0.80 | 0.8481(5)[49] | |||
| 0.8401(5)[49] | 0.80 | |||
| 0.85 | 0.7890(5)[49] | |||
| 0.90 | 0.7377(5)[49] | |||
| 0.95 | 0.6926(5)[49] |
카고메 격자:
| 격자 | z | 사이트 과집 임계값 | 본드 퍼콜레이션 임계값 | |
|---|---|---|---|---|
| 카고메 | 4 | 4 | 0.6711(4),[49] 0.67097(3)[50] | 0.95 |
| 0.6914(5),[49] 0.69210(2)[50] | 0.90 | |||
| 0.7162(5),[49] 0.71626(3)[50] | 0.85 | |||
| 0.7428(5),[49] 0.74339(3)[50] | 0.80 | |||
| 0.75 | 0.7894(9)[49] | |||
| 0.7757(8),[49] 0.77556(3)[50] | 0.75 | |||
| 0.80 | 0.7152(7)[49] | |||
| 0.81206(3)[50] | 0.70 | |||
| 0.85 | 0.6556(6)[49] | |||
| 0.85519(3)[50] | 0.65 | |||
| 0.90 | 0.6046(5)[49] | |||
| 0.90546(3)[50] | 0.60 | |||
| 0.95 | 0.5615(4)[49] | |||
| 0.96604(4)[50] | 0.55 | |||
| 0.9854(3)[50] | 0.53 |
* 다른 격자의 값은 사이트 본드 퍼콜레이션 조사를[49] 참조하십시오.
벌집형 격자의 현장 본드 퍼콜링에 대한 대략적인 공식
| 격자 | z | 임계값 | 메모들 | |
|---|---|---|---|---|
| (63) 벌집 | 3 | 3 | , When equal: ps = pb = 0.82199 | 근사 공식, p = 현장s 프로브, pb = 본드 프로브, pbc = 1 - 2 죄(π/18),[16] 정확히 ps=1, p=pbbc. |
아르키메데스 듀얼(레이브 격자)
라브스 격자는 아르키메데스 격자의 이중형이다. 도면 위치.[3] 균일 기울기를 참조하십시오.
| 격자 | z | 사이트 과집 임계값 | 본드 퍼콜레이션 임계값 | |
|---|---|---|---|---|
| 카이로 오각형 D(32,4,3,4)=(2/3)(53)+(1/3)(54) | 3,4 | 3⅓ | 0.6501834(2),[8] 0.650184(5)[3] | 0.585863... = 1 − pcbond(32,4,3,4) |
| 오각형 D(3,432)=(1/3)(54)+(2/3)(53) | 3,4 | 3⅓ | 0.6470471(2),[8] 0.647084(5),[3] 0.6471(6)[34] | 0.580358... = 1 − pcbond(33,42), 0.5800(6)[34] |
| D(3,64)=(1/5)(46)+(4/5)(4)(43)(4))(4)) | 3,6 | 3 3/5 | 0.639447[3] | 0.565694... = 1 - p(3cbond,64) |
| 주사위, 롬빌 타일링 D(3,6,3,6) = (1/3)(46) + (2/3)(43) | 3,6 | 4 | 0.5851(4),[51] 0.585040(5)[3] | 0.475595... = 1 − pcbond(3,6,3,6 ) |
| 루비 듀얼 D(3,4,6,4) = (1/6)(46) + (2/6)(43) + (3/6)(44) | 3,4,6 | 4 | 0.582410(5)[3] | 0.475167... = 1 − pcbond(3,4,6,4 ) |
| 유니언 잭, 테트라키스 사각 타일링 D(4,82) = (1/2)(34) + (1/2)(38) | 4,8 | 6 | 1/2 | 0.323197... = 1 - p(4cbond,82) |
| 이등분된 육각형,[52] 교차 이중 D(4,6,12)= (1/6)(312)+(2/6)+(16/2)(3)+(1/2)(34) | 4,6,12 | 6 | 1/2 | 0.306266... = 1 − pcbond(4,6,12) |
| 아사노하 (시드 리프)[53] D(3, 122)=(23/3)+(1/3)(312) | 3,12 | 6 | 1/2 | 0.259579... = 1 − pcbond(3, 122) |
2열 격자
상위 3개 격자: #13 #12 #36
하단 3개의 격자: #34 #37 #11
상위 2개 선반: 35위 30위
하단 2개의 격자: #41 #42
상위 4개 격자: 22위 23위 21위 20위
하단 3개의 격자: #16 #17 #15
상위 2개 격자: #31 #32
하단 격자: #33
| # | 격자 | z | 사이트 과집 임계값 | 본드 퍼콜레이션 임계값 | |
|---|---|---|---|---|---|
| 41 | (1/2)(3,4,3,12) + (1/2)(3, 122) | 4,3 | 3.5 | 0.7680(2)[54] | 0.67493252(36)[citation needed] |
| 42 | (1/3)(3,4,6,4) + (2/3)(4,6,12) | 4,3 | 31⁄3 | 0.7157(2)[54] | 0.64536587(40)[citation needed] |
| 36 | (1/7)(36) + (6/7)(32,4,12) | 6,4 | 4 2⁄7 | 0.6808(2)[54] | 0.55778329(40)[citation needed] |
| 15 | (2/3)(32,62) + (1/3)(3,6,3,6) | 4,4 | 4 | 0.6499(2)[54] | 0.53632487(40)[citation needed] |
| 34 | (1/7)(36) + (6/7)(32,62) | 6,4 | 4 2⁄7 | 0.6329(2)[54] | 0.51707873(70)[citation needed] |
| 16 | (4/5)(3,42,6) + (1/5)(3,6,3,6) | 4,4 | 4 | 0.6286(2)[54] | 0.51891529(35)[citation needed] |
| 17 | (4/5)(3,42,6) + (1/5)(3,6,3,6)* | 4,4 | 4 | 0.6279(2)[54] | 0.51769462(35)[citation needed] |
| 35 | (2/3)(3,42,6) + (1/3)(3,4,6,4) | 4,4 | 4 | 0.6221(2)[54] | 0.51973831(40)[citation needed] |
| 11 | (1/2)(34,6) + (1/2)(32,62) | 5,4 | 4.5 | 0.6171(2)[54] | 0.48921280(37)[citation needed] |
| 37 | (1/2)(33,42) + (1/2)(3,4,6,4) | 5,4 | 4.5 | 0.5885(2)[54] | 0.47229486(38)[citation needed] |
| 30 | (1/2)(32,4,3,4) + (1/2)(3,4,6,4) | 5,4 | 4.5 | 0.5883(2)[54] | 0.46573078(72)[citation needed] |
| 23 | (1/2)(33,42) + (1/2)(44) | 5,4 | 4.5 | 0.5720(2)[54] | 0.45844622(40)[citation needed] |
| 22 | (2/3)(33,42) + (1/3)(44) | 5,4 | 4 2⁄3 | 0.5648(2)[54] | 0.44528611(40)[citation needed] |
| 12 | (1/4)(36) + (3/4)(34,6) | 6,5 | 5 1⁄4 | 0.5607(2)[54] | 0.41109890(37)[citation needed] |
| 33 | (1/2)(33,42) + (1/2)(32,4,3,4) | 5,5 | 5 | 0.5505(2)[54] | 0.41628021(35)[citation needed] |
| 32 | (1/3)(33,42) + (2/3)(32,4,3,4) | 5,5 | 5 | 0.5504(2)[54] | 0.41549285(36)[citation needed] |
| 31 | (1/7)(36) + (6/7)(32,4,3,4) | 6,5 | 5 1⁄7 | 0.5440(2)[54] | 0.40379585(40)[citation needed] |
| 13 | (1/2)(36) + (1/2)(34,6) | 6,5 | 5.5 | 0.5407(2)[54] | 0.38914898(35)[citation needed] |
| 21 | (1/3)(36) + (2/3)(33,42) | 6,5 | 5 1⁄3 | 0.5342(2)[54] | 0.39491996(40)[citation needed] |
| 20 | (1/2)(36) + (1/2)(33,42) | 6,5 | 5.5 | 0.5258(2)[54] | 0.38285085(38)[citation needed] |
비균형 2-균일 격자
이 그림은 2-통일 격자 #37과 유사한 것을 보여주는데, 폴리곤이 모두 정규적이지 않다는 것, 즉 두 사각형 자리에 직사각형이 있다는 것, 그리고 폴리곤의 크기가 바뀐다는 것을 제외한다. 이 격자는 각 다각형이 단위 반지름 원 안에 새겨진 등각형 표현에 있다. 2-제복 격자의 두 칸은 이제 이등분 조건을 만족시키기 위해 하나의 직사각형으로 표현되어야 한다. 격자는 검은색 가장자리로 표시되고 이중 격자는 빨간색 점선으로 표시된다. 녹색 원은 원래 격자와 이중 격자 모두에 대해 이등선 구속조건을 나타낸다. 노란색 폴리곤은 격자 위에 있는 세 종류의 폴리곤을, 분홍색 폴리곤은 이중 격자 위에 있는 두 종류의 폴리곤을 강조한다. 격자에는 정점 유형(1/2)(33,42) + (1/2)(3,4,6,4)이 있고, 이중 격자에는 정점 유형(1/15)(4,156)+(6/1522)+(53)+(6/15)(5,4)이2 있다. 중요한 점은 긴 결합(격자와 이중 격자 모두)이 p = 2죄( sin/18) = 0.347296... 즉 삼각 격자 위의 결합 퍼콜 한계값이고, 짧은 결합은 점유 확률이 1 - 2 sin(π/18) = 0.652703이고, 이것은 육각 격자 위의 결합 퍼콜이다. 이러한 결과는 이등변환 조건에서[55] 나오지만 벌집형 격자의 특정 별에 항성삼각 변환을 적용함으로써 나타난다. 마지막으로, 긴 결합의 경우1 p1, p2, p3, p, 그리고 짧은 결합의 경우 1 - p, 1 - p2, 1 - p3 세 가지 다른 방향으로 세 가지 확률을 갖는 것으로 일반화할 수 있으며, 여기서 p1, p는2 비균형3 삼각 격자의 임계 표면을 만족한다.
2D 보우타이 및 마티니 격자의 임계값
왼쪽, 중앙, 오른쪽은 마티니 격자, 마티니-A 격자, 마티니-B 격자. 아래: 마티니 덮개/중간 격자, 카고메형 격자용 2×2, 1×1 서브넷(제거됨)과 동일.
일반화된 나비넥타이 격자(a-d) 및 격자 이중(e-h)의 몇 가지 다른 예:
| 격자 | z | 사이트 과집 임계값 | 본드 퍼콜레이션 임계값 | |
|---|---|---|---|---|
| 마티니(3/4)(3,92)+(1/4)(93) | 3 | 3 | 0.764826..., 1 + p4 − 3p3 = 0[56] | 0.707107... = 1/√2[57] |
| 나비넥타이(c) | 3,4 | 3 1/7 | 0.672929..., 1 − 2p3 − 2p4 − 2p5 − 7p6 + 18p7 + 11p8 − 35p9 + 21p10 − 4p11 = 0[58] | |
| 나비넥타이(d) | 3,4 | 3⅓ | 0.625457..., 1 − 2p2 − 3p3 + 4p4 − p5 = 0[58] | |
| 마티니-A(2/3)(3,72)+(1/3)(3,73) | 3,4 | 3⅓ | 1/√2[58] | 0.625457..., 1 − 2p2 − 3p3 + 4p4 − p5 = 0[58] |
| 나비넥타이 이중(e) | 3,4 | 3⅔ | 0.595482..., 1-pcbond(보우타이(a))[58] | |
| 나비넥타이(b) | 3,4,6 | 3⅔ | 0.533213..., 1 - p - 2p3 -4p-4p45+156+ 13p-36p78+19p9+p10 + p11=0[58] | |
| 마티니 커버/중간(1/2)(33,9) + (1/2)(3,9,3,9) | 4 | 4 | 0.707107... = 1/√2[57] | 0.57086651(33)[citation needed] |
| 마티니-B (1/2)(3,5,3,52) + (1/2)(3,52) | 3, 5 | 4 | 0.618034... = 2/(1 + √5), 1- p2 − p = 0[56][58] | 1/2[57][58] |
| 나비넥타이 이중(f) | 3,4,8 | 4 2/5 | 0.466787..., 1 - pcbond(보우타이(b))[58] | |
| 나비넥타이 (a) (1/2)(32,4,32,4) + (1/2)(3,4,3) | 4,6 | 5 | 0.5472(2),[34] 0.5479148(7)[59] | 0.404518..., 1 − p − 6p2 + 6p3 − p5 = 0[60][58] |
| 나비넥타이 이중(h) | 3,6,8 | 5 | 0.374543..., 1 - pcbond(보우 타이(d))[58] | |
| 나비넥타이 이중(g) | 3,6,10 | 5½ | 0.547... = pcsite(보우 타이(a)) | 0.327071..., 1 - pcbond(보우 타이(c))[58] |
| 마티니 이중(1/2)(33) + (1/2)(39) | 3,9 | 6 | 1/2 | 0.292893... = 1 − 1/√2[57] |
2D 커버링, 중간 및 일치 격자의 임계값
| 격자 | z | 사이트 과집 임계값 | 본드 퍼콜레이션 임계값 | |
|---|---|---|---|---|
| (4, 6, 12) 덮개/중간 | 4 | 4 | pcbond(4, 6, 12) = 0.693731... | 0.5593140(2),[8] 0.559315(1)[citation needed] |
| (42, 8) 덮개/중간, 사각 카고메 | 4 | 4 | pcbond(4,82) = 0.676803... | 0.544798017(4),[8] 0.54479793(34)[citation needed] |
| (34) 6) 중상 | 4 | 4 | 0.5247495(5)[8] | |
| (3,4,6,4) 중간 | 4 | 4 | 0.51276[8] | |
| (32, 4, 3, 4) 중병 | 4 | 4 | 0.512682929(8)[8] | |
| (3) 중용32 | 4 | 4 | 0.5125245984(9)[8] | |
| 평방 피복(비 평면) | 6 | 6 | 1/2 | 0.3371(1)[61] |
| 정사각형 일치 격자(비 평면) | 8 | 8 | 1 - pcsite(제곱) = 0.407253... | 0.25036834(6)[15] |
(4, 6, 12) 덮개/중간 격자
(4, 82) 덮개/중간 격자
(3,122) 덮개/중간 격자(빛 회색으로), 카고메(2 × 2) 서브넷에 해당하며, 검은색은 이러한 격자의 이중이다.
(왼쪽)(3,4,6,4) 덮개/중간 격자, (오른쪽)중간 이중(3,4,6,4) 중간격자, 빨간색 표시, 밝은 회색 바탕의 중간 격자. 왼쪽의 문양은 서양의 무덤탑인 카라칸의 이란식 기와에서 나타난다.
2D 키메라 비 평면 래치의 임계값
| 격자 | z | 사이트 과집 임계값 | 본드 퍼콜레이션 임계값 | |
|---|---|---|---|---|
| K(2,2) | 4 | 4 | 0.51253(14)[63] | 0.44778(15)[63] |
| K(3,3) | 6 | 6 | 0.43760(15)[63] | 0.35502(15)[63] |
| K(4,4) | 8 | 8 | 0.38675(7)[63] | 0.29427(12)[63] |
| K(5,5) | 10 | 10 | 0.35115(13)[63] | 0.25159(13)[63] |
| K(6,6) | 12 | 12 | 0.32232(13)[63] | 0.21942(11)[63] |
| K(7,7) | 14 | 14 | 0.30052(14)[63] | 0.19475(9)[63] |
| K(8,8) | 16 | 16 | 0.28103(11)[63] | 0.17496(10)[63] |
서브넷 래티스의 임계값
2 x 2, 3 x 3 및 4 x 4 서브넷 카고메 래치. 2 × 2 서브넷은 "삼각형 카고메" 격자로도 알려져 있다.[64]
| 격자 | z | 사이트 과집 임계값 | 본드 퍼콜레이션 임계값 | |
|---|---|---|---|---|
| Checkerboard – 2 × 2 서브넷 | 4,3 | 0.596303(1)[65] | ||
| 체커보드 – 4 × 4 서브넷 | 4,3 | 0.633685(9)[65] | ||
| Checkerboard – 8 x 8 서브넷 | 4,3 | 0.642318(5)[65] | ||
| Checkerboard – 16 × 16 서브넷 | 4,3 | 0.64237(1)[65] | ||
| 체커보드 – 32 × 32 서브넷 | 4,3 | 0.64219(2)[65] | ||
| Checkerboard – {\ \ 서브넷 | 4,3 | 0.642216(10)[65] | ||
| 카고메 – 2 × 2 서브넷 = (3, 122) 커버링/메디알 | 4 | pcbond (3, 122) = 0.74042077... | 0.600861966960(2),[8] 0.6008624(10),[16] 0.60086193(3)[6] | |
| 카고메 – 3 × 3 서브넷 | 4 | 0.6193296(10),[16] 0.61933176(5),[6] 0.61933044(32)[citation needed] | ||
| 카고메 – 4 × 4 서브넷 | 4 | 0.625365(3),[16] 0.62536424(7)[6] | ||
| 카고메 – 서브넷 | 4 | 0.628961(2)[16] | ||
| 카고메 – (1 × 1):(2 × 2) 서브넷 = 마티니 커버/중간 | 4 | pcbond(마티니) = 1/2/512 = 0.707107... | 0.57086648(36)[citation needed] | |
| 카고메 – (1 × 1):(3 × 3) 서브넷 | 4,3 | 0.728355596425196...[6] | 0.58609776(37)[citation needed] | |
| 카고메 – (1 × 1):(4 × 4) 서브넷 | 0.738348473943256...[6] | |||
| 카고메 – (1 × 1):(5 × 5) 서브넷 | 0.743548682503071...[6] | |||
| 카고메 – (1 × 1):(6 × 6) 서브넷 | 0.746418147634282...[6] | |||
| 카고메 – (2 × 2):(3 × 3) 서브넷 | 0.61091770(30)[citation needed] | |||
| 삼각형 – 2 x 2 서브넷 | 6,4 | 0.471628788[65] | ||
| 삼각형 – 3 x 3 서브넷 | 6,4 | 0.509077793[65] | ||
| 삼각형 – 4 × 4 서브넷 | 6,4 | 0.524364822[65] | ||
| 삼각형 – 5 x 5 서브넷 | 6,4 | 0.5315976(10)[65] | ||
| 삼각형 – 서브넷 | 6,4 | 0.53993(1)[65] |
랜덤 순차 흡착 객체의 임계값
(잠금 밀도에 대한 자세한 결과와 비교는 무작위 순차 흡착을 참조하십시오.)
| 계통 | z | 사이트 임계값 |
|---|---|---|
| 벌집 격자 위의 조광기 | 3 | 0.69,[66] 0.6653 [67] |
| 삼각 격자 위의 조광기 | 6 | 0.4872(8),[66] 0.4873,[67] 0.5157(2) [68] |
| 삼각 격자 위의 선형 4머 | 6 | 0.5220(2)[68] |
| 삼각 격자 위의 선형 8머 | 6 | 0.5281(5)[68] |
| 삼각 격자 위의 선형 12머 | 6 | 0.5298(8)[68] |
| 삼각 격자 위의 선형 16메르 | 6 | 0.5328(7)[68] |
| 삼각 격자 위의 선형 32머 | 6 | 0.5407(6)[68] |
| 삼각 격자 위에 놓인 선형 64메르 | 6 | 0.5455(4)[68] |
| 삼각 격자 위의 직선형 80머 | 6 | 0.5500(6)[68] |
| 선형 k { {\ \ \ 삼각형 격자 위에long. | 6 | 0.582(9)[68] |
| 조광기 및 5% 불순물, 삼각 격자 | 6 | 0.4832(7)[69] |
| 사각 격자 위의 평행 조광기 | 4 | 0.5863[70] |
| 사각 격자 위의 조광기 | 4 | 0.5617,[70] 0.5618(1),[71] 0.562,[72] 0.5713[67] |
| 정사각형 격자 위의 선형 3-메르 | 4 | 0.528[72] |
| 3-사이트 120° 각도, 불순물 5%, 삼각 격자 | 6 | 0.4574(9)[69] |
| 3개소 삼각형, 불순물 5% 삼각 격자 | 6 | 0.5222(9)[69] |
| 선형 트리머 및 5% 불순물, 삼각 격자 | 6 | 0.4603(8)[69] |
| 네모난 격자 위의 직선형 4머 | 4 | 0.504[72] |
| 정사각형 격자 위의 선형 5-메르 | 4 | 0.490[72] |
| 사각 격자 위의 선형 6-메어머 | 4 | 0.479[72] |
| 정사각형 격자 위의 선형 8머 | 4 | 0.474,[72] 0.4697(1)[71] |
| 정사각형 격자 위의 직선형 10머 | 4 | 0.469[72] |
| 정사각형 격자 위의 선형 16-메르 | 4 | 0.4639(1)[71] |
| 정사각형 격자 위의 직선형 32머 | 4 | 0.4747(2)[71] |
임계값은 사이트 과장이 처음 발생할 때(완전한 방해물이 아님) 객체에 의해 점유된 사이트의 비율을 제공한다. 더 긴 조광기는 참조를 참조하십시오.[73]
2차원 래치 전체 조광기 커버의 임계값
여기서 우리는 격자를 조광기로 덮어서 획득한 네트워크를 취급한 다음, 나머지 채권에 대한 결합 퍼콜레이션을 고려하고 있다. 이산수학에서 이 문제는 '완벽한 일치' 또는 '다이어 커버링' 문제로 알려져 있다.
| 계통 | z | 본드 임계값 |
|---|---|---|
| 평행 덮개, 사각 격자 | 6 | 0.381966...[74] |
| 시프트 커버, 사각 격자 | 6 | 0.347296...[74] |
| 엇갈린 덮개, 사각 격자 | 6 | 0.376825(2)[74] |
| 랜덤 커버, 사각 격자 | 6 | 0.367713(2)[74] |
| 평행 덮개, 삼각 격자 | 10 | 0.237418...[74] |
| 엇갈린 커버, 삼각 격자 | 10 | 0.237497(2)[74] |
| 랜덤 커버, 삼각 격자 | 10 | 0.235340(1)[74] |
정사각형 격자 위의 중합체 임계값(랜덤 워크)
시스템은 정사각형 격자 위의 일반(비항습) 무작위 길이 l로 구성된다.[75]
| l (길이) | z | 본드 퍼콜레이션 |
|---|---|---|
| 1 | 4 | 0.5(평균)[76] |
| 2 | 4 | 0.47697(4)[76] |
| 4 | 4 | 0.44892(6)[76] |
| 8 | 4 | 0.41880(4)[76] |
무작위 순차 흡착에 의해 추가된 길이 k의 자체 회피 보도의 임계값
| k | z | 사이트 임계값 | 본드 임계값 |
|---|---|---|---|
| 1 | 4 | 0.593(2)[77] | 0.5009(2)[77] |
| 2 | 4 | 0.564(2)[77] | 0.4859(2)[77] |
| 3 | 4 | 0.552(2)[77] | 0.4732(2)[77] |
| 4 | 4 | 0.542(2)[77] | 0.4630(2)[77] |
| 5 | 4 | 0.531(2)[77] | 0.4565(2)[77] |
| 6 | 4 | 0.522(2)[77] | 0.4497(2)[77] |
| 7 | 4 | 0.511(2)[77] | 0.4423(2)[77] |
| 8 | 4 | 0.502(2)[77] | 0.4348(2)[77] |
| 9 | 4 | 0.493(2)[77] | 0.4291(2)[77] |
| 10 | 4 | 0.488(2)[77] | 0.4232(2)[77] |
| 11 | 4 | 0.482(2)[77] | 0.4159(2)[77] |
| 12 | 4 | 0.476(2)[77] | 0.4114(2)[77] |
| 13 | 4 | 0.471(2)[77] | 0.4061(2)[77] |
| 14 | 4 | 0.467(2)[77] | 0.4011(2)[77] |
| 15 | 4 | 0.4011(2)[77] | 0.3979(2)[77] |
2D 불균형 래치의 임계값
| 격자 | z | 사이트 과집 임계값 | 본드 퍼콜레이션 임계값 |
|---|---|---|---|
| 비-비-비-비-비-비-본드 하나에 p = 1/2의 bow- | 3 | .3819654(5),[78]( - )/ 2 } |
2D 연속체 모델의 임계값
| 시스템 | Φc | ηc | nc |
|---|---|---|---|
| 반경 r의 디스크 | 0.67634831(2),[79] 0.6763475(6),[80] 0.676339(4),[81] 0.6764(4),[82] 0.6766(5),[83] 0.676(2),[84] 0.679,[85] 0.674[86] 0.676,[87] 0.680[88] | 1.1276(9),[89] 1.12808737(6),[79] 1.128085(2),[80] 1.128059(12),[81] 1.13,[90] 0.8[91] | 1.43632505(10),[92] 1.43632545(8),[79] 1.436322(2),[80] 1.436289(16),[81] 1.436320(4),[93] 1.436323(3),[94] 1.438(2),[95] 1.216 (48)[96] |
| 타원, ε = 1.5 | 0.0043[85] | 0.00431 | 2.059081(7)[94] |
| 타원, ε = 5/3 | 0.65[97] | 1.05[97] | 2.28[97] |
| 타원, 가로 세로 비율 ε = 2 | 0.6287945(12),[94] 0.63[97] | 0.991000(3),[94] 0.99[97] | 2.523560(8),[94] 2.5[97] |
| 타원, ε = 3 | 0.56[97] | 0.82[97] | 3.157339(8),[94] 3.14[97] |
| 타원, ε = 4 | 0.5[97] | 0.69[97] | 3.569706(8),[94] 3.5[97] |
| 타원, ε = 5 | 0.455,[85] 0.455,[87] 0.46[97] | 0.607[85] | 3.861262(12),[94] 3.86[85] |
| 타원, ε = 6 | 4.079365(17)[94] | ||
| 타원, ε = 7 | 4.249132(16)[94] | ||
| 타원, ε = 8 | 4.385302(15)[94] | ||
| 타원, ε = 9 | 4.497000(8)[94] | ||
| 타원, ε = 10 | 0.301,[85] 0.303,[87] 0.30[97] | 0.358[85] 0.36[97] | 4.590416(23)[94] 4.56,[85] 4.5[97] |
| 타원, ε = 15 | 4.894752(30)[94] | ||
| 타원, ε = 20 | 0.178,[85] 0.17[97] | 0.196[85] | 5.062313(39),[94] 4.99[85] |
| 타원, ε = 50 | 0.081[85] | 0.084[85] | 5.393863(28),[94] 5.38[85] |
| 타원, ε = 100 | 0.0417[85] | 0.0426[85] | 5.513464(40),[94] 5.42[85] |
| 타원, ε = 200 | 0.021[97] | 0.0212[97] | 5.40[97] |
| 타원, ε = 1000 | 0.0043[85] | 0.00431 | 5.624756(22),[94] 5.5 |
| 수페렐립스, ε = 1, m = 1.5 | 0.671[87] | ||
| 수페렐립스, ε = 2.5, m = 1.5 | 0.599[87] | ||
| 수페렐립스, ε = 5, m = 1.5 | 0.469[87] | ||
| 수페렐립스, ε = 10, m = 1.5 | 0.322[87] | ||
| 디스코 사각형, , = 1.5 | 1.894 [93] | ||
| 디스코 사각형, , = 2 | 2.245 [93] | ||
| 측면의 정렬된 사각형 | 0.66675(2),[44] 0.66674349(3),[79] 0.66653(1),[98] 0.6666(4),[99] 0.668[86] | 1.09884280(9),[79] 1.0982(3),[98] 1.098(1)[99] | 1.09884280(9),[79] 1.0982(3),[98] 1.098(1)[99] |
| 임의의 방향의 정사각형 | 0.62554075(4),[79] 0.6254(2)[99] 0.625,[87] | 0.9822723(1),[79] 0.9819(6)[99] 0.982278(14)[100] | 0.9822723(1),[79] 0.9819(6)[99] 0.982278(14)[100] |
| 직사각형, ε = 1.1 | 0.624870(7) | 0.980484(19) | 1.078532(21)[100] |
| 직사각형, ε = 2 | 0.590635(5) | 0.893147(13) | 1.786294(26)[100] |
| 직사각형, ε = 3 | 0.5405983(34) | 0.777830(7) | 2.333491(22)[100] |
| 직사각형, ε = 4 | 0.4948145(38) | 0.682830(8) | 2.731318(30)[100] |
| 직사각형, ε = 5 | 0.4551398(31), 0.451[87] | 0.607226(6) | 3.036130(28)[100] |
| 직사각형, ε = 10 | 0.3233507(25), 0.319[87] | 0.3906022(37) | 3.906022(37)[100] |
| 직사각형, ε = 20 | 0.2048518(22) | 0.2292268(27) | 4.584535(54)[100] |
| 직사각형, ε = 50 | 0.09785513(36) | 0.1029802(4) | 5.149008(20)[100] |
| 직사각형, ε = 100 | 0.0523676(6) | 0.0537886(6) | 5.378856(60)[100] |
| 직사각형, ε = 200 | 0.02714526(34) | 0.02752050(35) | 5.504099(69)[100] |
| 직사각형, ε = 1000 | 0.00559424(6) | 0.00560995(6) | 5.609947(60)[100] |
| 길이 | 5.6372858(6),[79] 5.63726(2),[101] 5.63724(18) [102] | ||
| 전원법 디스크, x=2.05 | 0.993(1)[103] | 4.90(1) | 0.0380(6) |
| 전원법 디스크, x=2.25 | 0.8591(5)[103] | 1.959(5) | 0.06930(12) |
| Power-law 디스크, x = 2.5 | 0.7836(4)[103] | 1.5307(17) | 0.09745(11) |
| 멱함수 디스크, x = | 0.69543(6)[103] | 1.18853(19) | 0.18916(3) |
| 멱함수 디스크, x = 5 | 0.68643(13)[103] | 1.1597(3) | 0.22149(8) |
| 멱함수 디스크, x = | 0.68241(8)[103] | 1.1470(1) | 0.24340(5) |
| 멱함수 디스크, x=7 | 0.6803(8)[103] | 1.140(6) | 0.25933(16) |
| 멱함수 디스크, x=8 | 0.67917(9)[103] | 1.1368(5) | 0.27140(7) |
| 멱함수 디스크, x = | 0.67856(12)[103] | 1.1349(4) | 0.28098(9) |
| radius 디스크 주위의 공극 | 1 - φc(디스크) = 0.32355169(2),[79] 0.318(2),[104] 0.3261(6)[105] |
= / r}}는 디스크의 임계 총 면적이며, 여기서 N은 개체 수, L은 시스템 크기입니다.
는 영향원 내의 디스크 센터 수(radius 2 r)를 제공한다.
= N {\{\ N은(는) 임계 디스크 반경이다.
= 와 b의 반장축과 반장축 타원의 경우 각각 / L 가로 세로 비율 = / b > b
for rectangles of dimensions and . Aspect ratio with .
for power-law distributed disks with , .
= - - c 은(는) 임계 면적 분율과 같다.
== N/ 는 단위 면적당 최대 길이 = 의 객체 수와 같다.
타원의 경우 c =( 4 / ) n_{_{c
void percolation의 경우 = - c {\ \^{-\_{는 임계 void fraction이다.
타원형 값에 대한 자세한 내용은 다음을 참조하십시오.
직사각형 값을 더 보려면
타원 및 직사각형 모두 supperellips에 속하며 / + / = 1 supperellips의 더 많은 percolation 값은 을 참조하십시오.[87]
모노디스페르스 입자 시스템의 경우, 오목형 슈퍼디스크의 퍼콜레이션 임계값을 에서와 같이 구한다.
디스크의 이진 분산에 대한 자세한 내용은 항목을 참조하십시오.
2D 랜덤 및 유사 지연 시간에 대한 임계값



| 격자 | z | 사이트 과집 임계값 | 본드 퍼콜레이션 임계값 | |
|---|---|---|---|---|
| 상대 근린 그래프 | 2.5576 | 0.796(2)[109] | 0.771(2)[109] | |
| 보로노이 테셀레이션 | 3 | 0.71410(2),[111] 0.7151*[54] | 0.68,[112] 0.6670(1),[113] 0.6680(5),[114] 0.666931(5)[111] | |
| 보로노이 덮개/중간 | 4 | 0.666931(2)[111][113] | 0.53618(2)[111] | |
| 랜덤화 카고메/제곱 옥타곤, 분수 r=1/2 | 4 | 0.6599[13] | ||
| 펜로즈롬브이듀얼 | 4 | 0.6381(3)[51] | 0.5233(2)[51] | |
| 가브리엘 그래프 | 4 | 0.6348(8),[115] 0.62[116] | 0.5167(6),[115] 0.52[116] | |
| 랜덤 라인 다듬기, 이중 | 4 | 0.586(2)[117] | ||
| 펜로즈롬브 | 4 | 0.5837(3),[51][119] 0.0.5610(6)(공채)[118] 0.58391(1) | 0.483(5),[120] 0.4770(2)[51] | |
| 팔각 격자, "화학" 링크(Ammann-Beenker tiling) | 4 | 0.585[121] | 0.48[121] | |
| 팔각 격자, "발광자성" 링크 | 5.17 | 0.543[121] | 0.40[121] | |
| 도십각 격자, "화학" 링크 | 3.63 | 0.628[121] | 0.54[121] | |
| 도십각 격자, "발광자성" 링크 | 4.27 | 0.617[121] | 0.495[121] | |
| 델라우나이 삼각측량 | 6 | 1/2[122] | 0.3333(1)[113] 0.3326(5),[114] 0.333069(2)[111] | |
| 통일 무한 평면 삼각 측량[123] | 6 | 1/2 | (2√3 – 1)/11 ≈ 0.2240[110][124] |
*이론적 추정치
상관 계수 ( r)~ - r 라고 가정함
| 격자무늬를 달다 | α | 사이트 과집 임계값 | 본드 퍼콜레이션 임계값 |
|---|---|---|---|
| 정사각형의 | 3 | 0.561406(4)[125] | |
| 정사각형의 | 2 | 0.550143(5)[125] | |
| 정사각형의 | 0.1 | 0.508(4)[125] |
슬래브의 임계값
h는 슬래브의 두께로 h × × × × ∞. 경계조건(b.c)은 슬래브의 상단면과 하단면을 가리킨다.
| 격자 | h | z | 사이트 과집 임계값 | 본드 퍼콜레이션 임계값 | |
|---|---|---|---|---|---|
| 심플 큐빅(개방형 b.c) | 2 | 5 | 5 | 0.47424,[126] 0.4756[127] | |
| bc(b.c. 개방) | 2 | 0.4155[127] | |||
| hcp (개방형 b.cp | 2 | 0.2828[127] | |||
| 다이아몬드(열린 B.C | 2 | 0.5451[127] | |||
| 심플 큐빅(개방형 b.c) | 3 | 0.4264[127] | |||
| bc(b.c. 개방) | 3 | 0.3531[127] | |||
| BCc(기존 B.C) | 3 | 0.21113018(38)[128] | |||
| hcp (개방형 b.cp | 3 | 0.2548[127] | |||
| 다이아몬드(열린 B.C | 3 | 0.5044[127] | |||
| 심플 큐빅(개방형 b.c) | 4 | 0.3997,[126] 0.3998[127] | |||
| bc(b.c. 개방) | 4 | 0.3232[127] | |||
| BCc(기존 B.C) | 4 | 0.20235168(59)[128] | |||
| hcp (개방형 b.cp | 4 | 0.2405[127] | |||
| 다이아몬드(열린 B.C | 4 | 0.4842[127] | |||
| 심플 큐빅(simple b.c.) | 5 | 6 | 6 | 0.278102(5)[128] | |
| 심플 큐빅(개방형 b.c) | 6 | 0.3708[127] | |||
| 심플 큐빅(simple b.c.) | 6 | 6 | 6 | 0.272380(2)[128] | |
| bc(b.c. 개방) | 6 | 0.2948[127] | |||
| hcp (개방형 b.cp | 6 | 0.2261[127] | |||
| 다이아몬드(열린 B.C | 6 | 0.4642[127] | |||
| 심플 큐빅(simple b.c.) | 7 | 6 | 6 | 0.3459514(12)[128] | 0.268459(1)[128] |
| 심플 큐빅(개방형 b.c) | 8 | 0.3557,[126] 0.3565[127] | |||
| 심플 큐빅(simple b.c.) | 8 | 6 | 6 | 0.265615(5)[128] | |
| bc(b.c. 개방) | 8 | 0.2811[127] | |||
| hcp (개방형 b.cp | 8 | 0.2190[127] | |||
| 다이아몬드(열린 B.C | 8 | 0.4549[127] | |||
| 심플 큐빅(개방형 b.c) | 12 | 0.3411[127] | |||
| bc(b.c. 개방) | 12 | 0.2688[127] | |||
| hcp (개방형 b.cp | 12 | 0.2117[127] | |||
| 다이아몬드(열린 B.C | 12 | 0.4456[127] | |||
| 심플 큐빅(개방형 b.c) | 16 | 0.3219,[126] 0.3339[127] | |||
| bc(b.c. 개방) | 16 | 0.2622[127] | |||
| hcp (개방형 b.cp | 16 | 0.2086[127] | |||
| 다이아몬드(열린 B.C | 16 | 0.4415[127] | |||
| 심플 큐빅(개방형 b.c) | 32 | 0.3219,[126] | |||
| 심플 큐빅(개방형 b.c) | 64 | 0.3165,[126] | |||
| 심플 큐빅(개방형 b.c) | 128 | 0.31398,[126] |
3D 격자의 임계값
| 격자 | z | 충진율* | 충전분수* | 사이트 과집 임계값 | 본드 퍼콜레이션 임계값 | ||
|---|---|---|---|---|---|---|---|
| (10,3)-산화물([129]또는 현장) | 23 32 | 2.4 | 0.748713(22)[129] | = (pc,bond(10,3) – a)1/2 = 0.742334(25)[130] | |||
| (10,3)-b산화물([129]또는 현장) | 23 32 | 2.4 | 0.233[131] | 0.174 | 0.745317(25)[129] | = (pc,bond(10,3) – b)1/2 = 0.739388(22)[130] | |
| 이산화규소([129]산소 사이트-산소 | 4,22 | 2 ⅔ | 0.638683(35)[129] | ||||
| 수정(10,3)-b[132] | 32,2 | 2 ⅔ | 0.627[132] | ||||
| (8,3)-a[130] | 3 | 3 | 0.577962(33)[130] | 0.555700(22)[130] | |||
| (10,3)-자이로이드[130][133] | 3 | 3 | 0.571404(40)[130] | 0.551060(37)[130] | |||
| (10,3)-b[130] | 3 | 3 | 0.565442(40)[130] | 0.546694(33)[130] | |||
| 입방산화물(산화물 현장-해당)[129] | 6,23 | 3.5 | 0.524652(50)[129] | ||||
| bc 이중 | 4 | 0.4560(6)[134] | 0.4031(6)[134] | ||||
| 아이스아이 | 4 | 4 | π √3 / 16 = 0.340087 | 0.147 | 0.433(11)[135] | 0.388(10)[136] | |
| 다이아몬드(얼음 Ic) | 4 | 4 | π √3 / 16 = 0.340087 | 0.1462332 | 0.4299(8),[137] 0.4299870(4),[138] 0.426(+0.08,–0.02),[139] 0.4297(4) [140] 0.4301(4),[141] 0.428(4),[142] 0.425(15),[143] 0.425,[37][42] 0.436(12),[135] | 0.3895892(5),[138] 0.3893(2),[141] 0.3893(3),[140] 0.388(5),[143] 0.3886(5),[137] 0.388(5)[142] 0.390(11),[136] | |
| 다이아몬드 이중 | 6 2/3 | 0.3904(5)[134] | 0.2350(5)[134] | ||||
| 3D 카고메(다이아몬드 격자 표시 그래프) | 6 | π √2 / 12 = 0.37024 | 0.1442 | 0.3895(2)[144] =다이아몬드 이중의 경우 pc(사이트) 및[134] 다이아몬드 격자의c 경우 p(사이트) | 0.2709(6)[134] | ||
| 보타이 스택 이중 | 5⅓ | 0.3480(4)[34] | 0.2853(4)[34] | ||||
| 벌집 쌓기 | 5 | 5 | 0.3701(2)[34] | 0.3093(2)[34] | |||
| 팔각 겹 이중 | 5 | 5 | 0.3840(4)[34] | 0.3168(4)[34] | |||
| 오각형 쌓기 | 5⅓ | 0.3394(4)[34] | 0.2793(4)[34] | ||||
| 카고메 스택 | 6 | 6 | 0.453450 | 0.1517 | 0.3346(4)[34] | 0.2563(2)[34] | |
| FCC 이중 | 42,8 | 5 1/3 | 0.3341(5)[134] | 0.2703(3)[134] | |||
| 심플 큐빅 | 6 | 6 | π / 6 = 0.5235988 | 0.1631574 | 0.307(10),[143] 0.307,[37] 0.3115(5),[145] 0.3116077(2),[146] 0.311604(6),[147] 0.311605(5),[148] 0.311600(5),[149] 0.3116077(4),[150] 0.3116081(13),[151] 0.3116080(4),[152] 0.3116060(48),[153] 0.3116004(35),[154] 0.31160768(15)[138] | 0.247(5),[143] 0.2479(4),[137] 0.2488(2),[155] 0.24881182(10),[146] 0.2488125(25),[156] 0.2488126(5),[157] | |
| hcp 듀얼 | 44,82 | 5 1/3 | 0.3101(5)[134] | 0.2573(3)[134] | |||
| 주사위를 던지다 | 5,8 | 6 | π √3 / 9 = 0.604600 | 0.1813 | 0.2998(4)[34] | 0.2378(4)[34] | |
| 나비넥타이 스택 | 7 | 7 | 0.2822(6)[34] | 0.2092(4)[34] | |||
| 쌓인 삼각형/단순 육각형 | 8 | 8 | 0.26240(5),[158] 0.2625(2),[159] 0.2623(2)[34] | 0.18602(2),[158] 0.1859(2)[34] | |||
| 팔각형(조합-잭) 쌓기 | 6,10 | 8 | 0.2524(6)[34] | 0.1752(2)[34] | |||
| bcc | 8 | 8 | 0.243(10),[143] 0.243,[37] 0.2459615(10),[152] 0.2460(3),[160] 0.2464(7),[137] 0.2458(2)[141] | 0.178(5),[143] 0.1795(3),[137] 0.18025(15),[155] 0.1802875(10),[157] | |||
| 3NN으로 단순 큐빅(BC와 동일) | 8 | 8 | 0.2455(1),[161] 0.2457(7)[162] | ||||
| FCC, D3 | 12 | 12 | π / (3 √2) = 0.740480 | 0.147530 | 0.195,[37] 0.198(3),[163] 0.1998(6),[137] 0.1992365(10),[152] 0.19923517(20),[138] 0.1994(2),[141] 0.199236(4)[164] | 0.1198(3),[137] 0.1201635(10)[157] 0.120169(2)[164] | |
| hcp | 12 | 12 | π / (3 √2) = 0.740480 | 0.147545 | 0.195(5),[143] 0.1992555(10)[165] | 0.1201640(10)[165] 0.119(2)[143] | |
| 라2−x4 스르x Cu O | 12 | 12 | 0.19927(2)[166] | ||||
| 2NN을 사용한 단순 큐빅(FC와 동일) | 12 | 12 | 0.1991(1)[161] | ||||
| NN+4N으로 심플 큐빅 | 12 | 12 | 0.15040(12)[167] | 0.1068263(7)[168] | |||
| 3N+4N으로 심플 큐빅 | 14 | 14 | 0.20490(12)[167] | 0.1012133(7)[168] | |||
| BCc NN+2N (=sc(3,4) sc-3N+4N) | 14 | 14 | 0.175,[37] 0.1686(20)[169] | 0.0991(5)[169] | |||
| FCC의 나노튜브 섬유 | 14 | 14 | 0.1533(13)[170] | ||||
| NN+3N으로 심플 큐빅 | 14 | 14 | 0.1420(1)[161] | 0.0920213(7)[168] | |||
| 2N+4N으로 심플 큐빅 | 18 | 18 | 0.15950(12)[167] | 0.0751589(9)[168] | |||
| NN+2N으로 심플 큐빅 | 18 | 18 | 0.137,[42] 0.136[171] 0.1372(1),[161] 0.13735(5)[citation needed] | 0.0752326(6) [168] | |||
| NN+2N을 사용하는 FCC(=sc-2NN+4N) | 18 | 18 | 0.136[37] | ||||
| 단거리 상관 관계가 있는 심플 큐빅 | 6+ | 6+ | 0.126(1)[172] | ||||
| NN+3N+4로 심플 큐빅NN | 20 | 20 | 0.11920(12)[167] | 0.0624379(9)[168] | |||
| 2N+3N으로 심플 큐빅 | 20 | 20 | 0.1036(1)[161] | 0.0629283(7)[168] | |||
| NN+2N+4로 심플 큐빅NN | 24 | 24 | 0.11440(12)[167] | 0.0533056(6)[168] | |||
| 2N+3N+4로 심플 큐빅NN | 26 | 26 | 0.11330(12)[167] | 0.0474609(9) | |||
| NN+2N+3으로 심플 큐빅NN | 26 | 26 | 0.097,[37] 0.0976(1),[161] 0.0976445(10)[citation needed] | 0.0497080(10)[168] | |||
| BCc(NN+2N+3 포함)NN | 26 | 26 | 0.095[42] | ||||
| NN+2N+3N+4로 심플 큐빅NN | 32 | 32 | 0.10000(12)[167] | 0.0392312(8)[168] | |||
| NN+2N+3으로 FCCNN | 42 | 42 | 0.061,[42] 0.0610(5)[171] | ||||
| NN+2N+3N+4를 사용하는 FCCNN | 54 | 54 | 0.0500(5)[171] |
충전 계수 = 모든 격자 부위에서 구를 만짐으로써 채워진 공간의 일부(균일한 결합 길이를 가진 시스템의 경우만 해당) 원자성 패킹 팩터라고도 한다.
채우기 비율(또는 중요 채우기 비율) = 채우기 비율 * pc(사이트)
NN = 가장 가까운 이웃, 2NN = 가장 가까운 이웃, 3NN = 가장 가까운 이웃 등
질문: hcp와 FCC 격자의 채권 임계값은 작은 통계 오류 내에서 일치한다. 그들은 동일한가? 그리고 만약 그렇지 않다면, 그들은 얼마나 멀리 떨어져 있는가? 어느 문턱이 더 클 것으로 예상되나? 얼음과 다이아몬드 격자에도 유사하다. 참조
| 시스템 | 폴리머 φc |
|---|---|
| 피부 중합체 매트릭스의 제외 부피(입방 격자 상의 적층 모델)를 과대 채색한다. | 0.4304(3)[174] |
3D 단위의 조광기 퍼콜레이션
| 시스템 | 사이트 과집 임계값 | 본드 퍼콜레이션 임계값 |
|---|---|---|
| 심플 큐빅 | 0.2555(1)[175] |
3D 연속체 모델의 임계값
걸린 구와 폴리머 매트릭스를 제외하고 모두 겹친다.
| 시스템 | Φc | ηc |
|---|---|---|
| 반지름의 구 r | 0.289,[176] 0.293,[177] 0.286,[178] 0.295.[86] 0.2895(5),[179] 0.28955(7),[180] 0.2896(7),[181] 0.289573(2),[182] 0.2896,[183] 0.2854,[184] 0.290,[185] 0.290[186] | 0.3418(7),[179] 0.341889(3),[182] 0.3360,[184] 0.34189(2), 0.341935(8) |
| 주요 반지름 r 및 가로 세로 비율이 4/3인 타원형 제거 | 0.2831[184] | 0.3328[184] |
| 경미한 반경 r 및 가로 세로 비율 3/2의 프로레이트 타원체 | 0.2757,[183] 0.2795,[184] 0.2763[185] | 0.3278[184] |
| 주요 반지름 r 및 가로 세로 비율을 가진 타원형 지우기 2 | 0.2537,[183] 0.2629,[184] 0.254[185] | 0.3050[184] |
| 경미한 반경 r 및 가로 세로 비율 2의 프로레이트 타원체 | 0.2537,[183] 0.2618,[184] 0.25(2),[188] 0.2507[185] | 0.3035,[184] 0.29(3)[188] |
| 주요 반지름 r 및 가로 세로 비율을 가진 타원형 지우기 3 | 0.2289[184] | 0.2599[184] |
| 경미한 반경 r 및 가로 세로 비율 3의 프로레이트 타원체 | 0.2033,[183] 0.2244,[184] 0.20(2)[188] | 0.2541,[184] 0.22(3)[188] |
| 주요 반지름 r 및 가로 세로 비율을 가진 타원형 지우기 4 | 0.2003[184] | 0.2235[184] |
| 경미한 반지름 r 및 가로 세로 비율 4의 프로레이트 타원체 | 0.1901,[184] 0.16(2)[188] | 0.2108,[184] 0.17(3)[188] |
| 주요 반지름 r 및 가로 세로 비율이 5인 타원형 지우기 | 0.1757[184] | 0.1932[184] |
| 경미한 반경 r 및 가로 세로 비율 5의 프로레이트 타원체 | 0.1627,[184] 0.13(2)[188] | 0.1776,[184] 0.15(2)[188] |
| 주요 반지름 r 및 가로 세로 비율을 가진 타원형 지우기 10 | 0.0895,[183] 0.1058[184] | 0.1118[184] |
| 경미한 반경 r 및 가로 세로 비율을 가진 프로레이트 타원체 10 | 0.0724,[183] 0.08703,[184] 0.07(2)[188] | 0.09105,[184] 0.07(2)[188] |
| 주요 반지름 r 및 가로 세로 비율이 100인 타원형 지우기 | 0.01248[184] | 0.01256[184] |
| 경미한 반경 r 및 가로 세로 비율 100인 프로레이트 타원체 | 0.006949[184] | 0.006973[184] |
| 주요 반지름 r 및 가로 세로 비율이 1000인 타원형 지우기 | 0.001275[184] | 0.001276[184] |
| 주요 반지름 r 및 가로 세로 비율이 2000인 타원형 지우기 | 0.000637[184] | 0.000637[184] |
| H/D = 1인 Spherocylinder | 0.2439(2)[181] | |
| H/D = 4인 Spherocylinder | 0.1345(1)[181] | |
| H/D = 10인 Spherocylinder | 0.06418(20)[181] | |
| H/D = 50인 Spherocylinder | 0.01440(8)[181] | |
| H/D = 100인 Spherocylinder | 0.007156(50)[181] | |
| H/D = 200인 Spherocylinder | 0.003724(90)[181] | |
| 정렬 실린더 | 0.2819(2)[189] | 0.3312(1)[189] |
| 의 정렬된 큐브= a | 0.2773(2)[99] 0.27727(2),[44] 0.27730261(79)[153] | 0.3247(3),[98] 0.3248(3),[99] 0.32476(4)[189] 0.324766(1)[153] |
| 무작위 이코사헤드라 | 0.3030(5)[190] | |
| 무작위 방향 도데카헤드라 | 0.2949(5)[190] | |
| 임의지향옥타헤드라 | 0.2514(6)[190] | |
| 의 임의 방향 큐브= | 0.2168(2)[99] 0.2174,[183] | 0.2444(3),[99] 0.2443(5)[190] |
| 무작위 방향 사방면체 | 0.1701(7)[190] | |
| radius의 랜덤 방향 디스크(3D | 0.9614(5)[191] | |
| 측면 의 랜덤 방향 사각판 | 0.8647(6)[191] | |
| 측면 / 3 / r 의 랜덤 방향 삼각판 | 0.7295(6)[191] | |
| radius 디스크 주위의 공극 | 22.86(2)[192] | |
| 주요 반경 r 및 가로 세로 비율의 타원형 지우기 주위의 공극 10 | 15.42(1)[192] | |
| 주요 반지름 r 및 가로 세로 비율 2의 타원형 지우기 주위의 공극 | 6.478(8)[192] | |
| 반구 주위의 공극 | 0.0455(6)[193] | |
| 정렬된 테트라헤드라 주변의 공극 | 0.0605(6)[194] | |
| 회전 사면체 주위의 공극 | 0.0605(6)[194] | |
| 정렬된 큐브 주위의 공극 | 0.036(1),[44] 0.0381(3)[194] | |
| 회전된 큐브 주위의 공극 | 0.0381(3)[194] | |
| 정렬된 옥타헤드라 주변의 공극 | 0.0407(3)[194] | |
| 회전된 옥타헤드라 주변의 공극 | 0.0398(5)[194] | |
| 정렬된 도데카헤드라 주변의 공극 | 0.0356(3)[194] | |
| 회전 도데카헤드라 주변의 공극 | 0.0360(3)[194] | |
| 정렬된 이코사헤드라 주변의 공극 | 0.0346(3)[194] | |
| 회전 이코사헤드라 주변의 공극 | 0.0336(7)[194] | |
| 구 주변의 공극 | 0.034(7),[195] 0.032(4),[196] 0.030(2),[104] 0.0301(3),[197] 0.0294,[198] 0.0300(3),[199] 0.0317(4),[200] 0.0308(5)[193] 0.0301(1)[194] | 3.506(8),[199] 3.515(6),[192] 3.510(2)[89] |
| 걸린 구(평균 z = 6) | 0.19(3),[201] 0.190,[202] 걸린 구체의 접촉 네트워크도 참조한다. | 0.59(1)[201] |
=(/ ) r / L 은 총 볼륨(구)이며, 여기서 N은 개체 수, L은 시스템 크기이다.
= - e - c 는 임계 볼륨 비율이다.
디스크와 플레이트의 경우 유효 볼륨 및 볼륨 분율이다.
보이드("스위스-치즈" 모델)의 , = e - {c {\e^{-\c}}}는 임계 보이드 분율이다.
타원형 및 타원형 플레이트 주위의 보이드 퍼콜레이션에 대한 자세한 결과는 을 참조하십시오.[192]
타원체 퍼콜레이션 값을 더 보려면 을 참조하십시오.[184]
Spherocylinder의 경우 H/D는 실린더의 지름에 대한 높이의 비율로, 그 다음 반구에 의해 덮인다. 추가 값이 제공된다.[181]
슈퍼볼의 경우 m은 변형 파라미터로, 퍼콜레이션 값이 에 제시되며,[203][204] 오목형 슈퍼볼의 한계값도 에 결정된다.
큐보이드와 같은 입자의 경우 m은 변형 파라미터로, 더 많은 퍼콜레이션 값이 제공된다.[183]
3D 랜덤 및 유사 지연 시간에 대한 임계값
| 격자 | z | 사이트 과집 임계값 | 본드 퍼콜레이션 임계값 | |
|---|---|---|---|---|
| 포장된 구체의 접촉 네트워크 | 6 | 0.310(5),[201] 0.287(50),[205] 0.3116(3),[202] | ||
| 랜덤 평면 다듬기, 이중 | 6 | 0.290(7)[206] | ||
| 이코사헤드랄 펜로즈 | 6 | 0.285[207] | 0.225[207] | |
| 대각선 2개가 있는 펜로즈 | 6.764 | 0.271[207] | 0.207[207] | |
| 8개의 대각선이 있는 펜로즈 | 12.764 | 0.188[207] | 0.111[207] | |
| 보로노이 네트워크 | 15.54 | 0.1453(20)[169] | 0.0822(50)[169] |
다른 3D 모델에 대한 임계값
| 격자 | z | 사이트 과집 임계값 | 본드 퍼콜레이션 임계값 | |
|---|---|---|---|---|
| 드릴링 퍼콜레이션, 단순 큐빅 격자* | 6 | 6 | 6345(3),[208] 0.6339(5),[209] 0.633965(15)[210] | |
| 랜덤 튜브 모델, 단순 입방 격자† | 0.231456(6)[211] |
드릴링 퍼콜레이션에서 사이트 임계값은 제거되지 않은 열의 분율을 나타낸다.
2개의 인접한 욕조의 제가 거기{\displaystyle h_{나는}h}은 이 오버랩 높이 튜브 여과에서 †면 채권 기준}}, μ이 이웃 수직 튜브 세그먼트 간의 유대감 확률은 1− e− μ h 같은 나는{\displaystyle 1-e^{-\mu h_{나는}{\displaystyle \mu}매개 변수의 가치를 나타낸다.e 분절[211]
여러 치수 공간의 임계값
고차원의 연속체 모델
| d | 시스템 | Φc | ηc |
|---|---|---|---|
| 4 | 겹치는 하이퍼스피어 | 0.1223(4)[98] | 0.1304(5)[98] |
| 4 | 정렬된 하이퍼큐브 | 0.1132(5),[98] 0.1132348(17) [153] | 0.1201(6)[98] |
| 4 | 하이퍼스피어 주변의 공극 | 0.00211(2)[105] | 6.161(10),[105] 6.248(2),[89] |
| 5 | 겹치는 하이퍼스피어 | 0.05443(7)[98] | |
| 5 | 정렬된 하이퍼큐브 | 0.04900(7),[98] 0.0481621(13),[153] | 0.05024(7)[98] |
| 5 | 하이퍼스피어 주변의 공극 | 1.26(6)x10−4 [105] | 8.98(4),[105] 9.170(8),[89] |
| 6 | 겹치는 하이퍼스피어 | 0.02339(5)[98] | |
| 6 | 정렬된 하이퍼큐브 | 0.02082(8),[98] 0.0213479(10)[153] | 0.02104(8)[98] |
| 6 | 하이퍼스피어 주변의 공극 | 8.0(6)x10−6 [105] | 11.74(8),[105] 12.24(2),[89] |
| 7 | 겹치는 하이퍼스피어 | 0.01051(3)[98] | |
| 7 | 정렬된 하이퍼큐브 | 0.00999(5),[98] 0.0097754(31)[153] | 0.01004(5)[98] |
| 7 | 하이퍼스피어 주변의 공극 | 15.46(5)[89] | |
| 8 | 겹치는 하이퍼스피어 | 0.004904(6)[98] | |
| 8 | 정렬된 하이퍼큐브 | 0.004498(5)[98] | |
| 8 | 하이퍼스피어 주변의 공극 | 18.64(8)[89] | |
| 9 | 겹치는 하이퍼스피어 | 0.002353(4)[98] | |
| 9 | 정렬된 하이퍼큐브 | 0.002166(4)[98] | |
| 9 | 하이퍼스피어 주변의 공극 | 22.1(4)[89] | |
| 10 | 겹치는 하이퍼스피어 | 0.001138(3)[98] | |
| 10 | 정렬된 하이퍼큐브 | 0.001058(4)[98] | |
| 11 | 겹치는 하이퍼스피어 | 0.0005530(3)[98] | |
| 11 | 정렬된 하이퍼큐브 | 0.0005160(3)[98] |
4d에서는 =( / 2) 2 /
5d에서는 =( / ) 2 r /
6d에서 = (/ 6) 3 6 /
= - e - c 는 임계 볼륨 비율이다.
보이드 모델의 경우 c= - c 는 임계 보이드 비율이며, 는 중복 객체의 총 볼륨이다.
하이퍼 큐브 격자의 임계값
| d | z | 사이트 임계값 | 본드 임계값 |
|---|---|---|---|
| 4 | 8 | 0.198(1)[212] 0.197(6),[213] 0.1968861(14),[214] 0.196889(3),[215] 0.196901(5),[216] 0.19680(23),[217] 0.1968904(65),[153] 0.19688561(3)[218] | 0.16005(15),[155] 0.1601314(13),[214] 0.160130(3),[215] 0.1601310(10),[156] 0.1601312(2),[219] 0.16013122(6)[218] |
| 5 | 10 | 0.141(1),0.198(1)[212] 0.141(3),[213] 0.1407966(15),[214] 0.1407966(26),[153] 0.14079633(4)[218] | 0.11819(4),[155] 0.118172(1),[214] 0.1181718(3)[156] 0.11817145(3)[218] |
| 6 | 12 | 0.106(1),[212] 0.108(3),[213] 0.109017(2),[214] 0.1090117(30),[153] 0.109016661(8)[218] | 0.0942(1),[220] 0.0942019(6),[214] 0.09420165(2)[218] |
| 7 | 14 | 0.05950(5),[220] 0.088939(20),[221] 0.0889511(9),[214] 0.0889511(90),[153] 0.088951121(1),[218] | 0.078685(30),[220] 0.0786752(3),[214] 0.078675230(2)[218] |
| 8 | 16 | 0.0752101(5),[214] 0.075210128(1)[218] | 0.06770(5),[220] 0.06770839(7),[214] 0.0677084181(3)[218] |
| 9 | 18 | 0.0652095(3),[214] 0.0652095348(6)[218] | 0.05950(5),[220] 0.05949601(5),[214] 0.0594960034(1)[218] |
| 10 | 20 | 0.0575930(1),[214] 0.0575929488(4)[218] | 0.05309258(4),[214] 0.0530925842(2)[218] |
| 11 | 22 | 0.05158971(8),[214] 0.0515896843(2)[218] | 0.04794969(1),[214] 0.04794968373(8)[218] |
| 12 | 24 | 0.04673099(6),[214] 0.0467309755(1)[218] | 0.04372386(1),[214] 0.04372385825(10)[218] |
| 13 | 26 | 0.04271508(8),[214] 0.04271507960(10)[218] | 0.04018762(1),[214] 0.04018761703(6)[218] |
고차원 하이퍼큐브 래치에 대한 임계값은 점근성 시리즈 확장이 있음
여기서 = -
기타 고차원 격자의 임계값
| d | 격자무늬를 달다 | z | 사이트 임계값 | 본드 임계값 |
|---|---|---|---|---|
| 4 | 다이아몬드 | 5 | 0.2978(2)[141] | 0.2715(3)[141] |
| 4 | 카고메 | 8 | 0.2715(3)[144] | 0.177(1) [141] |
| 4 | bcc | 16 | 0.1037(3)[141] | 0.074(1),[141] 0.074212(1)[219] |
| 4 | FCC, D4 | 24 | 0.0842(3),[141] 0.08410(23),[217] 0.0842001(11)[164] | 0.049(1),[141] 0.049517(1),[219] 0.0495193(8)[164] |
| 4 | 세제곱 NN+2N | 32 | 0.06190(23)[217] | 0.035827(1)[219] |
| 4 | 세제곱 3N | 32 | 0.04540(23)[217] | |
| 4 | 세제곱 NN+3N | 40 | 0.04000(23)[217] | |
| 4 | 세제곱 2N+3N | 58 | 0.03310(23)[217] | |
| 4 | 세제곱 NN+2N+3NN | 64 | 0.03190(23)[217] | |
| 5 | 다이아몬드 | 6 | 0.2252(3)[141] | 0.2084(4)[144] |
| 5 | 카고메 | 10 | 0.2084(4)[144] | 0.130(2)[141] |
| 5 | bcc | 32 | 0.0446(4)[141] | 0.033(1)[141] |
| 5 | FCC, D5 | 40 | 0.0431(3),[141] 0.0435913(6)[164] | 0.026(2),[141] 0.0271813(2)[164] |
| 6 | 다이아몬드 | 7 | 0.1799(5)[141] | 0.1677(7)[144] |
| 6 | 카고메 | 12 | 0.1677(7)[144] | |
| 6 | FCC, D6 | 60 | 0.0252(5),[141] 0.02602674(12)[164] | 0.01741556(5)[164] |
| 6 | bcc | 64 | 0.0199(5)[141] | |
| 6 | E6[164] | 72 | 0.02194021(14)[164] | 0.01443205(8)[164] |
| 7 | FCC, D7 | 84 | 0.01716730(5)[164] | 0.012217868(13)[164] |
| 7 | E7[164] | 126 | 0.01162306(4)[164] | 0.00808368(2)[164] |
| 8 | FCC, D8 | 112 | 0.01215392(4)[164] | 0.009081804(6)[164] |
| 8 | E8[164] | 240 | 0.00576991(2)[164] | 0.004202070(2)[164] |
| 9 | FCC, D9 | 144 | 0.00905870(2)[164] | 0.007028457(3)[164] |
| 9 | [164] | 272 | 0.00480839(2)[164] | 0.0037006865(11)[164] |
| 10 | FCC, D10 | 180 | 0.007016353(9)[164] | 0.005605579(6)[164] |
| 11 | FCC, D11 | 220 | 0.005597592(4)[164] | 0.004577155(3)[164] |
| 12 | FCC, D12 | 264 | 0.004571339(4)[164] | 0.003808960(2)[164] |
| 13 | FCC, D13 | 312 | 0.003804565(3)[164] | 0.0032197013(14)[164] |
1차원 장거리 퍼콜의 임계값
1차원 체인에서 우리는 나 그냥 j확률 p과 함께 C=나는 j1−{j\displaystyle}{\displaystyle 나는} 뚜렷한 사이트+σ{\displaystyle p={\frac{C}{i-j ^{1+\sigma}}}}멱수 σ 을을 바로 멱함수로 부패하는;0{\displaystyle \sigma>0}. Percolation occurs[225]사이에 채권을 확립한다.한 criti에[226] 값 < < 1 숫자로 결정된 과대포장 임계값은 다음과 같이 지정된다.[224]
| 0.1 | 0.047685(8) |
| 0.2 | 0.093211(16) |
| 0.3 | 0.140546(17) |
| 0.4 | 0.193471(15) |
| 0.5 | 0.25482(5) |
| 0.6 | 0.327098(6) |
| 0.7 | 0.413752(14) |
| 0.8 | 0.521001(14) |
| 0.9 | 0.66408(7) |
쌍곡선, 계층 및 트리 격자의 임계값
이러한 격자에는 두 가지 퍼콜레이션 임계값이 있을 수 있다. 즉, 하한 임계값은 무한 군집이 나타나는 확률보다 높고, 상한은 고유한 무한 군집이 있는 확률이다.


| 격자 | z | 사이트 과집 임계값 | 본드 퍼콜레이션 임계값 | |||
|---|---|---|---|---|---|---|
| 더 낮게 | 상부 | 더 낮게 | 상부 | |||
| 쌍곡선 {3,7} | 7 | 7 | 0.26931171(7),[229] 0.20[230] | 0.73068829(7),[229] 0.73(2)[230] | 0.20,[231] 0.1993505(5)[229] | 0.37,[231] 0.4694754(8)[229] |
| 쌍곡선 {3,8} | 8 | 8 | 0.20878618(9)[229] | 0.79121382(9)[229] | 0.1601555(2)[229] | 0.4863559(6)[229] |
| 쌍곡선 {3,9} | 9 | 9 | 0.1715770(1)[229] | 0.8284230(1)[229] | 0.1355661(4)[229] | 0.4932908(1)[229] |
| 쌍곡선 {4,5} | 5 | 5 | 0.29890539(6)[229] | 0.8266384(5)[229] | 0.27,[231] 0.2689195(3)[229] | 0.52,[231] 0.6487772(3) [229] |
| 쌍곡선 {4,6} | 6 | 6 | 0.22330172(3)[229] | 0.87290362(7)[229] | 0.20714787(9)[229] | 0.6610951(2)[229] |
| 쌍곡선 {4,7} | 7 | 7 | 0.17979594(1)[229] | 0.89897645(3)[229] | 0.17004767(3)[229] | 0.66473420(4)[229] |
| 쌍곡선 {4,8}개 | 8 | 8 | 0.151035321(9)[229] | 0.91607962(7)[229] | 0.14467876(3)[229] | 0.66597370(3)[229] |
| 쌍곡선 {4,9} | 8 | 8 | 0.13045681(3)[229] | 0.92820305(3)[229] | 0.1260724(1)[229] | 0.66641596(2)[229] |
| {5,5} 쌍곡선 | 5 | 5 | 0.26186660(5)[229] | 0.89883342(7)[229] | 0.263(10),[232] 0.25416087(3)[229] | 0.749(10)[232] 0.74583913(3)[229] |
| {7,3} 쌍곡선 | 3 | 3 | 0.54710885(10)[229] | 0.8550371(5),[229] 0.86(2)[230] | 0.53,[231] 0.551(10),[232] 0.5305246(8)[229] | 0.72,[231] 0.810(10),[232] 0.8006495(5)[229] |
| {1987,3} 카이리 트리 | 3 | 3 | 1/2 | 1/2[231] | 1[231] | |
| 향상된 이진 트리(EBT) | 0.304(1),[233] 0.306(10),[232] (√13 − 3)/2 = 0.302776[234] | 0.48,[231] 0.564(1),[233] 0.564(10),[232] 1/2[234] | ||||
| 향상된 이진 트리 이중 | 0.436(1),[233] 0.452(10)[232] | 0.696(1),[233] 0.699(10)[232] | ||||
| 비플래너 하노이 네트워크(HN-NP) | 0.319445[228] | 0.381996[228] | ||||
| 조부모님과 함께한 케일리 트리 | 8 | 0.158656326[235] | ||||
참고: {m,n}은(는) 슐래플리 기호로, 모든 꼭지점에서 n개의 일반 m-곤이 만나는 쌍곡선 격자를 의미한다.
For bond percolation on {P,Q}, we have by duality . For site percolation, because of the self-matching of triangulated lattices.
조정 번호 z: pc = 1 / (z - 1)의 Cayley 트리(베스트 격자)
Cayley tree with a distribution of z with mean , mean-square pc= [236] (site or bond threshold)
지시된 퍼콜레이션에 대한 임계값
| 격자 | z | 사이트 과집 임계값 | 본드 퍼콜레이션 임계값 |
|---|---|---|---|
| (1+1)-d 벌집 | 1.5 | 0.8399316(2),[237] 0.839933(5),[238]= i e) 1+1)-d sq 중. | 0.8228569(2),[237] 0.82285680(6)[237] |
| (1+1)-d 카고메 | 2 | 0.7369317(2),[237] 0.73693182(4)[239] | 0.6589689(2),[237] 0.65896910(8)[237] |
| (1+1)-d 제곱, 대각선 | 2 | 0.705489(4),[240] 0.705489(4),[241] 0.70548522(4),[242] 0.70548515(20),[239] 0.7054852(3),[237] | 0.644701(2),[243] 0.644701(1),[244] 0.644701(1),[240] 0.6447006(10),[238] 0.64470015(5),[245] 0.644700185(5),[242] 0.6447001(2),[237] 0.643(2)[246] |
| (1+1)-d 삼각형 | 3 | 0.595646(3),[240] 0.5956468(5),[245] 0.5956470(3)[237] | 0.478018(2),[240] 0.478025(1),[245] 0.4780250(4)[237] 0.479(3)[246] |
| (2+1)-d 단순 입방면, 대각선 평면 | 3 | 0.43531(1),[247] 0.43531411(10)[237] | 0.382223(7),[247] 0.38222462(6)[237] 0.383(3)[246] |
| (2+1)-d 제곱 nn (= bcc) | 4 | 0.3445736(3),[248] 0.344575(15)[249] 0.3445740(2)[237] | 0.2873383(1),[250] 0.287338(3)[247] 0.28733838(4)[237] 0.287(3)[246] |
| (2+1)-d FCC | 0.199(2))[246] | ||
| (3+1)-d 하이퍼큐브, 대각선 | 4 | 0.3025(10),[251] 0.30339538(5) [237] | 0.26835628(5),[237] 0.2682(2)[246] |
| (3+1)-d 입방체, nn | 6 | 0.2081040(4)[248] | 0.1774970(5)[156] |
| (3+1)-d bcc | 8 | 0.160950(30),[249] 0.16096128(3)[237] | 0.13237417(2)[237] |
| (4+1)-d 하이퍼큐브, 대각선 | 5 | 0.23104686(3)[237] | 0.20791816(2),[237] 0.2085(2)[246] |
| (4+1)-d 하이퍼큐브, nn | 8 | 0.1461593(2),[248] 0.1461582(3)[252] | 0.1288557(5)[156] |
| (4+1)-d bcc | 16 | 0.075582(17)[249] | 0.063763395(5)[237] |
| (5+1)-d 하이퍼큐브, 대각선 | 6 | 0.18651358(2)[237] | 0.170615155(5),[237] 0.1714(1) [246] |
| (5+1)-d 하이퍼큐브, nn | 10 | 0.1123373(2)[248] | 0.1016796(5)[156] |
| (5+1)-d 하이퍼큐브 bc | 32 | 0.035967(23),[249] 0.035972540(3)[237] | 0.0314566318(5)[237] |
| (6+1)-d 하이퍼큐브, 대각선 | 7 | 0.15654718(1)[237] | 0.145089946(3),[237] 0.1458[246] |
| (6+1)-d 하이퍼큐브, nn | 12 | 0.0913087(2)[248] | 0.0841997(14)[156] |
| (6+1)-d 하이퍼큐브 bc | 64 | 0.017333051(2)[237] | 0.01565938296(10)[237] |
| (7+1)-d 하이퍼큐브, 대각선 | 8 | 0.135004176(10)[237] | 0.126387509(3),[237] 0.1270(1) [246] |
| (7+1)-d 하이퍼큐브,nn | 14 | 0.07699336(7)[248] | 0.07195(5)[156] |
| (7+1)-d bcc | 128 | 0.008 432 989(2)[237] | 0.007 818 371 82(6)[237] |
nn = 가장 가까운 이웃. a (d + 1)차원 하이퍼큐브 시스템의 경우 하이퍼큐브는 d 치수로 되어 있고 시간 방향은 2D 가장 가까운 이웃을 가리킨다.
이종 시스템의 정확한 임계 다지관
균질하지 않은 삼각 격자 결합 퍼콜레이션[17]
균질하지 않은 벌집형 격자 결합 퍼콜레이션 = 카고메 격자 부위 퍼콜레이션[17]
균질하지 않은(3,12^2) 격자, 현장 퍼콜레이션[4]
or
비균종 유니언-잭 격자, , 2, p , {\이(가) 있는 사이트 퍼콜레이션
Inhomogeneous 마티니 격자, 채권 여과[58][255]1−(p1p2 이렇게 3+p2p3r1+p1p3r2)−(p1p2r1r2+p1p3r1r3+p2p3r2r3)+p1p2p3(r1r2+r1r3+r2r3)+{\displaysty.르 1-(p_{
균질하지 않은 마티니 격자, 현장 퍼콜. r = 항성 내 부지
균질하지 않은 마티니-A(3–7) 격자, 본드 퍼콜레이션. 왼쪽(A에서 아래쪽까지): r , 1 오른쪽 ,p , 2 교차 결합:
균질하지 않은 마티니-B(3–5) 격자, 본드 퍼콜레이션
채권의 외부를 둘러싸는 삼각형을Inhomogeneous 마티니 격자, 확률, y x내부에서 외부에 z{\displaystyle y,x,z}, 채권 여과[255]1− 3z+z3−(1− z2)[3x2이 어두워져서(1+y− y 2)(1+ z+x3y2(3− 2y)(1+2z])0{\displaystyle 1-3z+z^{3}(1-z^{2})는 경우에는 3x^{2}y.(1+y-
불균형 체커보드 격자, 결합 퍼콜레이션
where are the four bonds around the square and is the diagonal bond connecting the vertex between bonds and .
그래프의 경우
공간에 포함되지 않은 랜덤 그래프의 경우 퍼콜레이션 임계값을 정확하게 계산할 수 있다. 예를 들어, 모든 노드의 도 k가 같은 임의의 일반 그래프의 경우c, p=1/k. Poissonian 학위 분포를 포함한 Erds-Rény(ER) 그래프의 경우 pc=1/<k>.[256] 임계 임계값은 상호의존적인 ER 네트워크의 네트워크에도 대해 정확히 계산되었다.[257][258]
참고 항목
- 2D 퍼콜레이션 클러스터
- 방향 퍼콜레이션
- 유효 매체 근사치
- 선반 위의 전염병 모델
- 그래프 이론
- 네트워크 과학
- 퍼콜레이션
- 과집합 임계 지수
- 퍼콜레이션 이론
- 부트스트랩 퍼콜레이션
- 무작위 순차 흡착
- 균일 틸팅
참조
- ^ Kasteleyn, P. W.; Fortuin, C. M. (1969). "Phase transitions in lattice systems with random local properties". Journal of the Physical Society of Japan Supplement. 26: 11–14. Bibcode:1969PSJJS..26...11K.
- ^ a b c d e Grünbaum, Branko & Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. ISBN 978-0-7167-1193-3.
- ^ a b c d e f g Parviainen, Robert (2005). Connectivity Properties of Archimedean and Laves Lattices. Diva. Vol. 34. Uppsala Dissertations in Mathematics. p. 37. ISBN 978-91-506-1751-1.
- ^ a b c d e f g h i Suding, P. N.; R. M. Ziff (1999). "Site percolation thresholds for Archimedean lattices". Physical Review E. 60 (1): 275–283. Bibcode:1999PhRvE..60..275S. doi:10.1103/PhysRevE.60.275. PMID 11969760.
- ^ a b c d e f g Parviainen, Robert (2007). "Estimation of bond percolation thresholds on the Archimedean lattices". Journal of Physics A. 40 (31): 9253–9258. arXiv:0704.2098. Bibcode:2007JPhA...40.9253P. doi:10.1088/1751-8113/40/31/005. S2CID 680787.
- ^ a b c d e f g h i Ding, Chengxiang; Zhe Fu. Wenan Guo; F. Y. Wu (2010). "Critical frontier for the Potts and percolation models on triangular-type and kagome-type lattices II: Numerical analysis". Physical Review E. 81 (6): 061111. arXiv:1001.1488. Bibcode:2010PhRvE..81f1111D. doi:10.1103/PhysRevE.81.061111. PMID 20866382. S2CID 29625353.
- ^ a b Scullard, C. R.; J. L. Jacobsen (2012). "Transfer matrix computation of generalised critical polynomials in percolation". arXiv:1209.1451 [cond-mat.stat-mech].
- ^ a b c d e f g h i j k l m n o p q r s t u v Jacobsen, J. L. (2014). "High-precision percolation thresholds and Potts-model critical manifolds from graph polynomials". Journal of Physics A. 47 (13): 135001. arXiv:1401.7847. Bibcode:2014JPhA...47m5001G. doi:10.1088/1751-8113/47/13/135001. S2CID 119614758.
- ^ a b Jacobsen, Jesper L.; Christian R. Scullard (2013). "Critical manifolds, graph polynomials, and exact solvability" (PDF). StatPhys 25, Seoul, Korea July 21–26.
- ^ a b c d e f g h Scullard, Christian R.; Jesper Lykke Jacobsen (2020). "Bond percolation thresholds on Archimedean lattices from critical polynomial roots". Physical Review Research. 2 (1): 012050. arXiv:1910.12376. Bibcode:2020PhRvR...2a2050S. doi:10.1103/PhysRevResearch.2.012050. S2CID 204904858.
- ^ a b c d e d'Iribarne, C.; G. Resigni; M. Resigni (1995). "Determination of site percolation transitions for 2D mosaics by means of the minimal spanning tree approach". Physics Letters A. 209 (1–2): 95–98. Bibcode:1995PhLA..209...95D. doi:10.1016/0375-9601(95)00794-8.
- ^ a b c d e f g h i d'Iribarne, C.; Rasigni, M.; Rasigni, G. (1999). "From lattice long-range percolation to the continuum one". Phys. Lett. A. 263 (1–2): 65–69. Bibcode:1999PhLA..263...65D. doi:10.1016/S0375-9601(99)00585-X.
- ^ a b Schliecker, G.; C. Kaiser (1999). "Percolation on disordered mosaics". Physica A. 269 (2–4): 189–200. Bibcode:1999PhyA..269..189S. doi:10.1016/S0378-4371(99)00093-X.
- ^ Djordjevic, Z. V.; H. E. Stanley; Alla Margolina (1982). "Site percolation threshold for honeycomb and square lattices". Journal of Physics A. 15 (8): L405–L412. Bibcode:1982JPhA...15L.405D. doi:10.1088/0305-4470/15/8/006.
- ^ a b c d e Feng, Xiaomei; Youjin Deng; H. W. J. Blöte (2008). "Percolation transitions in two dimensions". Physical Review E. 78 (3): 031136. arXiv:0901.1370. Bibcode:2008PhRvE..78c1136F. doi:10.1103/PhysRevE.78.031136. PMID 18851022. S2CID 29282598.
- ^ a b c d e f g Ziff, R. M.; Hang Gu (2008). "Universal relation for critical percolation thresholds of kagome-class lattices".
{{cite journal}}: Cite 저널은 필요로 한다.journal=(도움말) - ^ a b c d e Sykes, M. F.; J. W. Essam (1964). "Exact critical percolation probabilities for site and bond problems in two dimensions". Journal of Mathematical Physics. 5 (8): 1117–1127. Bibcode:1964JMP.....5.1117S. doi:10.1063/1.1704215.
- ^ Ziff, R. M.; P. W. Suding (1997). "Determination of the bond percolation threshold for the kagome lattice". Journal of Physics A. 30 (15): 5351–5359. arXiv:cond-mat/9707110. Bibcode:1997JPhA...30.5351Z. doi:10.1088/0305-4470/30/15/021. S2CID 28814369.
- ^ Scullard, C. R. (2012). "Percolation critical polynomial as a graph invariant". Physical Review E. 86 (4): 1131. arXiv:1111.1061. Bibcode:2012PhRvE..86d1131S. doi:10.1103/PhysRevE.86.041131. PMID 23214553. S2CID 33348328.
- ^ a b Jacobsen, J. L. (2015). "Critical points of Potts and O(N) models from eigenvalue identities in periodic Temperley-Lieb algebras". Journal of Physics A. 48 (45): 454003. arXiv:1507.03027. Bibcode:2015JPhA...48S4003L. doi:10.1088/1751-8113/48/45/454003. S2CID 119146630.
- ^ Lin, Keh Ying; Wen Jong Ma (1983). "Two-dimensional Ising model on a ruby lattice". Journal of Physics A. 16 (16): 3895–3898. Bibcode:1983JPhA...16.3895L. doi:10.1088/0305-4470/16/16/027.
- ^ Derrida, B.; D. Stauffer (1985). "Corrections to scaling and phenomenological renormalization for 2-dimensional percolation and lattice animal problems". J. Physique. 46 (45): 1623. doi:10.1051/jphys:0198500460100162300. S2CID 8289499.
- ^ Yang, Y.; S. Zhou.; Y. Li. (2013). "Square++: Making a connection game win-lose complementary and playing-fair". Entertainment Computing. 4 (2): 105–113. doi:10.1016/j.entcom.2012.10.004.
- ^ Newman, M. E. J.; R. M. Ziff (2000). "Efficient Monte-Carlo algorithm and high-precision results for percolation". Physical Review Letters. 85 (19): 4104–7. arXiv:cond-mat/0005264. Bibcode:2000PhRvL..85.4104N. CiteSeerX 10.1.1.310.4632. doi:10.1103/PhysRevLett.85.4104. PMID 11056635. S2CID 747665.
- ^ de Oliveira, P.M.C.; R. A. Nobrega, D. Stauffer. (2003). "Corrections to finite size scaling in percolation". Brazilian Journal of Physics. 33 (3): 616–618. arXiv:cond-mat/0308525. Bibcode:2003BrJPh..33..616O. doi:10.1590/S0103-97332003000300025. S2CID 8972025.
- ^ Lee, M. J. (2007). "Complementary algorithms for graphs and percolation". Physical Review E. 76 (2): 027702. arXiv:0708.0600. Bibcode:2007PhRvE..76b7702L. doi:10.1103/PhysRevE.76.027702. PMID 17930184. S2CID 304257.
- ^ Lee, M. J. (2008). "Pseudo-random-number generators and the square site percolation threshold". Physical Review E. 78 (3): 031131. arXiv:0807.1576. Bibcode:2008PhRvE..78c1131L. doi:10.1103/PhysRevE.78.031131. PMID 18851017. S2CID 7027694.
- ^ Levenshteĭn, M. E.; B. I. Shklovskiĭ; M. S. Shur; A. L. Éfros (1975). "The relation between the critical exponents of percolation theory". Zh. Eksp. Teor. Fiz. 69: 386–392. Bibcode:1975JETP...42..197L.
- ^ Dean, P.; N. F. Bird (1967). "Monte Carlo estimates of critical percolation probabilities". Proc. Camb. Phil. Soc. 63 (2): 477–479. Bibcode:1967PCPS...63..477D. doi:10.1017/s0305004100041438.
- ^ Dean, P (1963). "A new Monte Carlo method for percolation problems on a lattice". Proc. Camb. Phil. Soc. 59∂malarg (2): 397–410. Bibcode:1963PCPS...59..397D. doi:10.1017/s0305004100037026.
- ^ Tencer, John; Forsberg, Kelsey Meeks (2021). "Postprocessing techniques for gradient percolation predictions on the square lattice". Phys. Rev. E. 103 (1): 012115. Bibcode:2021PhRvE.103a2115T. doi:10.1103/PhysRevE.103.012115. OSTI 1778027. PMID 33601521. S2CID 231961701.
- ^ Betts, D. D. (1995). "A new two-dimensional lattice of coordination number five". Proc. Nova Scotian Inst. Sci. 40: 95–100. hdl:10222/35332.
- ^ a b d'Iribarne, C.; G. Resigni; M. Resigni (1999). "Minimal spanning tree and percolation on mosaics: graph theory and percolation". J. Phys. A: Math. Gen. 32 (14): 2611–2622. Bibcode:1999JPhA...32.2611D. doi:10.1088/0305-4470/32/14/002.
- ^ a b c d e f g h i j k l m n o p q r s t u v w van der Marck, S. C. (1997). "Percolation thresholds and universal formulas". Physical Review E. 55 (2): 1514–1517. Bibcode:1997PhRvE..55.1514V. doi:10.1103/PhysRevE.55.1514.
- ^ a b c d e f Malarz, K.; S. Galam (2005). "Square-lattice site percolation at increasing ranges of neighbor bonds". Physical Review E. 71 (1): 016125. arXiv:cond-mat/0408338. Bibcode:2005PhRvE..71a6125M. doi:10.1103/PhysRevE.71.016125. PMID 15697676.
- ^ a b c d e f g h i j k l m n o p q r s t u v w x y z aa Majewski, M.; K. Malarz (2007). "Square lattice site percolation thresholds for complex neighbourhoods". Acta Phys. Pol. B. 38 (38): 2191. arXiv:cond-mat/0609635. Bibcode:2007AcPPB..38.2191M.
- ^ a b c d e f g h i j Dalton, N. W.; C. Domb; M. F. Sykes (1964). "Dependence of critical concentration of a dilute ferromagnet on the range of interaction". Proc. Phys. Soc. 83 (3): 496–498. doi:10.1088/0370-1328/83/3/118.
- ^ Collier, Andrew. "Percolation Threshold: Including Next-Nearest Neighbours".
- ^ a b c d e f g h i j k l m n Ouyang, Yunqing; Y. Deng; Henk W. J. Blöte (2018). "Equivalent-neighbor percolation models in two dimensions: Crossover between mean-field and short-range behavior". Phys. Rev. E. 98 (6): 062101. arXiv:1808.05812. Bibcode:2018PhRvE..98f2101O. doi:10.1103/PhysRevE.98.062101. S2CID 119328197.
- ^ a b Xu, Wenhui; Junfeng Wang; Hao Hu; Youjin Deng (2021). "Critical polynomials in the nonplanar and continuum percolation models". Physical Review E. 103 (2): 022127. arXiv:2010.02887. Bibcode:2021PhRvE.103b2127X. doi:10.1103/PhysRevE.103.022127. ISSN 2470-0045. PMID 33736116. S2CID 222140792.
- ^ a b c d e f g Malarz, Krzysztof (2020). "Site percolation thresholds on triangular lattice with complex neighborhoods". Chaos: An Interdisciplinary Journal of Nonlinear Science. 30 (12): 123123. arXiv:2006.15621. Bibcode:2020Chaos..30l3123M. doi:10.1063/5.0022336. PMID 33380057. S2CID 220250058.
- ^ a b c d e f Domb, C.; N. W. Dalton (1966). "Crystal statistics with long-range forces I. The equivalent neighbour model". Proc. Phys. Soc. 89 (4): 859–871. Bibcode:1966PPS....89..859D. doi:10.1088/0370-1328/89/4/311.
- ^ a b c d e Gouker, Mark; Family, Fereydoon (1983). "Evidence for classical critical behavior in long-range site percolation". Phys. Rev. B. 28 (3): 1449. Bibcode:1983PhRvB..28.1449G. doi:10.1103/PhysRevB.28.1449.
- ^ a b c d e f g h i Koza, Zbigniew; Kondrat, Grzegorz; Suszczyński, Karol (2014). "Percolation of overlapping squares or cubes on a lattice". Journal of Statistical Mechanics: Theory and Experiment. 2014 (11): P11005. arXiv:1606.07969. Bibcode:2014JSMTE..11..005K. doi:10.1088/1742-5468/2014/11/P11005. S2CID 118623466.
- ^ a b c Deng, Youjin; Yunqing Ouyang; Henk W. J. Blöte (2019). "Medium-range percolation in two dimensions". J. Phys.: Conf. Ser. 1163 (1): 012001. Bibcode:2019JPhCS1163a2001D. doi:10.1088/1742-6596/1163/1/012001.
- ^ a b c Scullard, C. R.; R. M. Ziff (2010). "Critical surfaces for general inhomogeneous bond percolation problems". Journal of Statistical Mechanics: Theory and Experiment. 2010 (3): P03021. arXiv:0911.2686. Bibcode:2010JSMTE..03..021S. doi:10.1088/1742-5468/2010/03/P03021. S2CID 119230786.
- ^ a b Wu, F. Y. (1979). "Critical point of planar Potts models". Journal of Physics C. 12 (17): L645–L650. Bibcode:1979JPhC...12L.645W. doi:10.1088/0022-3719/12/17/002.
- ^ a b c d e f g Hovi, J.-P.; A. Aharony (1996). "Scaling and universality in the spanning probability for percolation". Physical Review E. 53 (1): 235–253. Bibcode:1996PhRvE..53..235H. doi:10.1103/PhysRevE.53.235. PMID 9964253.
- ^ a b c d e f g h i j k l m n o p q r s Tarasevich, Yuriy Yu; Steven C. van der Marck (1999). "An investigation of site-bond percolation on many lattices". Int. J. Mod. Phys. C. 10 (7): 1193–1204. arXiv:cond-mat/9906078. Bibcode:1999IJMPC..10.1193T. doi:10.1142/S0129183199000978. S2CID 16917458.
- ^ a b c d e f g h i j González-Flores, M. I.; A. A. Torres; W. Lebrecht; A. J. Ramirez-Pastor (2021). "Site-bond percolation in two-dimensional kagome lattices: Analytical approach and numerical simulations". Phys. Rev. E. 104 (1): 014130. Bibcode:2021PhRvE.104a4130G. doi:10.1103/PhysRevE.104.014130. PMID 34412224. S2CID 237243188.
- ^ a b c d e Sakamoto, S.; F. Yonezawa and M. Hori (1989). "A proposal for the estimation of percolation thresholds in two-dimensional lattices". J. Phys. A. 22 (14): L699–L704. Bibcode:1989JPhA...22L.699S. doi:10.1088/0305-4470/22/14/009.
- ^ Deng, Y.; Y. Huang, J. L. Jacobsen, J. Salas, and A. D. Sokal (2011). "Finite-temperature phase transition in a class of four-state Potts antiferromagnets". Physical Review Letters. 107 (15): 150601. arXiv:1108.1743. Bibcode:2011PhRvL.107o0601D. doi:10.1103/PhysRevLett.107.150601. PMID 22107278. S2CID 31777818.
{{cite journal}}: CS1 maint : 복수이름 : 작성자 목록(링크) - ^ Syozi, I (1972). "Transformation of Ising Models". In Domb, C.; Green, M. S. (eds.). Phase Transitions in Critical Phenomena. Vol. 1. Academic Press, London. pp. 270–329.
- ^ a b c d e f g h i j k l m n o p q r s t u Neher, Richard; Mecke, Klaus and Wagner, Herbert (2008). "Topological estimation of percolation thresholds". Journal of Statistical Mechanics: Theory and Experiment. 2008 (1): P01011. arXiv:0708.3250. Bibcode:2008JSMTE..01..011N. doi:10.1088/1742-5468/2008/01/P01011. S2CID 8584164.
{{cite journal}}: CS1 maint : 복수이름 : 작성자 목록(링크) - ^ Grimmett, G.; Manolescu, I (2012). "Bond percolation on isoradial graphs: Criticality and universality". Probability Theory and Related Fields. 159 (1–2): 273–327. arXiv:1204.0505. doi:10.1007/s00440-013-0507-y. S2CID 15031903.
- ^ a b Scullard, C. R. (2006). "Exact site percolation thresholds using a site-to-bond transformation and the star-triangle transformation". Physical Review E. 73 (1): 016107. arXiv:cond-mat/0507392. Bibcode:2006PhRvE..73a6107S. doi:10.1103/PhysRevE.73.016107. PMID 16486216. S2CID 17948429.
- ^ a b c d Ziff, R. M. (2006). "Generalized cell–dual-cell transformation and exact thresholds for percolation". Physical Review E. 73 (1): 016134. Bibcode:2006PhRvE..73a6134Z. doi:10.1103/PhysRevE.73.016134. PMID 16486243.
- ^ a b c d e f g h i j k l m Scullard, C. R.; Robert M Ziff (2006). "Exact bond percolation thresholds in two dimensions". Journal of Physics A. 39 (49): 15083–15090. arXiv:cond-mat/0610813. Bibcode:2006JPhA...3915083Z. doi:10.1088/0305-4470/39/49/003. S2CID 14332146.
- ^ Ding, Chengxiang; Yancheng Wang; Yang Li (2012). "Potts and percolation models on bowtie lattices". Physical Review E. 86 (2): 021125. arXiv:1203.2244. Bibcode:2012PhRvE..86b1125D. doi:10.1103/PhysRevE.86.021125. PMID 23005740. S2CID 27190130.
- ^ Wierman, John (1984). "A bond percolation critical probability determination based on the star-triangle transformation". J. Phys. A: Math. Gen. 17 (7): 1525–1530. Bibcode:1984JPhA...17.1525W. doi:10.1088/0305-4470/17/7/020.
- ^ Ziff, R. M.; Scullard, C. R. (2010). "Critical surfaces for general inhomogeneous bond percolation problems". Journal of Statistical Mechanics: Theory and Experiment. 2010 (3): P03021. arXiv:0911.2686. Bibcode:2010JSMTE..03..021S. doi:10.1088/1742-5468/2010/03/P03021. S2CID 119230786.
- ^ [1][2]
- ^ a b c d e f g h i j k l m n Melchert, Oliver; Helmut G. Katzgraber; Mark A. Novotny (2016). "Site and bond percolation thresholds in Kn,n-based lattices: Vulnerability of quantum annealers to random qubit and coupler failures on Chimera topologies". Physical Review E. 93 (4): 042128. arXiv:1511.07078. Bibcode:2016PhRvE..93d2128M. doi:10.1103/PhysRevE.93.042128. PMID 27176275. S2CID 206249608.
- ^ Okubo, S.; M. Hayashi, S. Kimura, H. Ohta, M. Motokawa, H. Kikuchi and H. Nagasawa (1998). "Submillimeter wave ESR of triangular-kagome antiferromagnet Cu9X2(cpa)6 (X=Cl, Br)". Physica B. 246--247 (2): 553–556. Bibcode:1998PhyB..246..553O. doi:10.1016/S0921-4526(97)00985-X.
{{cite journal}}: CS1 maint : 복수이름 : 작성자 목록(링크) - ^ a b c d e f g h i j k Haji Akbari, Amir; R. M. Ziff (2009). "Percolation in networks with voids and bottlenecks". Physical Review E. 79 (2): 021118. arXiv:0811.4575. Bibcode:2009PhRvE..79b1118H. doi:10.1103/PhysRevE.79.021118. PMID 19391717. S2CID 2554311.
- ^ a b Cornette, V.; A. J. Ramirez-Pastor; F. Nieto (2003). "Dependence of the percolation threshold on the size of the percolating species". Physica A. 327 (1): 71–75. Bibcode:2003PhyA..327...71C. doi:10.1016/S0378-4371(03)00453-9.
- ^ a b c Lebrecht, W.; P. M. Centres; A. J. Ramirez-Pastor (2019). "Analytical approximation of the site percolation thresholds for monomers and dimers on two-dimensional lattices". Physica A. 516: 133–143. Bibcode:2019PhyA..516..133L. doi:10.1016/j.physa.2018.10.023. S2CID 125418069.
- ^ a b c d e f g h i Longone, Pablo; P.M. Centres; A. J. Ramirez-Pastor (2019). "Percolation of aligned rigid rods on two-dimensional triangular lattices". Physical Review E. 100 (5): 052104. arXiv:1906.03966. Bibcode:2019PhRvE.100e2104L. doi:10.1103/PhysRevE.100.052104. PMID 31870027. S2CID 182953009.
- ^ a b c d Budinski-Petkovic, Lj; I. Loncarevic; Z. M. Jacsik; and S. B. Vrhovac (2016). "Jamming and percolation in random sequential adsorption of extended objects on a triangular lattice with quenched impurities". Journal of Statistical Mechanics: Theory and Experiment. 2016 (5): 053101. Bibcode:2016JSMTE..05.3101B. doi:10.1088/1742-5468/2016/05/053101. S2CID 3913989.
- ^ a b Cherkasova, V. A.; Yu. Yu. Tarasevich; N. I. Lebovka; and N.V. Vygornitskii (2010). "Percolation of the aligned dimers on a square lattice". Eur. Phys. J. B. 74 (2): 205–209. arXiv:0912.0778. Bibcode:2010EPJB...74..205C. doi:10.1140/epjb/e2010-00089-2. S2CID 118485353.
- ^ a b c d Leroyer, Y.; E. Pommiers (1994). "Monte Carlo analysis of percolation of line segments on a square lattice". Phys. Rev. B. 50 (5): 2795–2799. arXiv:cond-mat/9312066. Bibcode:1994PhRvB..50.2795L. doi:10.1103/PhysRevB.50.2795. PMID 9976520.
- ^ a b c d e f g Vanderwalle, N.; S. Galam; M. Kramer (2000). "A new universality for random sequential deposition of needles". Eur. Phys. J. B. 14 (3): 407–410. arXiv:cond-mat/0004271. Bibcode:2000EPJB...14..407V. doi:10.1007/s100510051047. S2CID 11142384.
- ^ Kondrat, Grzegorz; Andrzej Pękalski (2001). "Percolation and jamming in random sequential adsorption of linear segments on a square lattice". Phys. Rev. E. 63 (5): 051108. arXiv:cond-mat/0102031. Bibcode:2001PhRvE..63e1108K. doi:10.1103/PhysRevE.63.051108. PMID 11414888. S2CID 44490067.
- ^ a b c d e f g Haji-Akbari, A.; Nasim Haji-Akbari; Robert M. Ziff (2015). "Dimer Covering and Percolation Frustration". Phys. Rev. E. 92 (3): 032134. arXiv:1507.04411. Bibcode:2015PhRvE..92c2134H. doi:10.1103/PhysRevE.92.032134. PMID 26465453. S2CID 34100812.
- ^ Zia, R. K. P.; W. Yong; B. Schmittmann (2009). "Percolation of a collection of finite random walks: a model for gas permeation through thin polymeric membranes". Journal of Mathematical Chemistry. 45: 58–64. doi:10.1007/s10910-008-9367-6. S2CID 94092783.
- ^ a b c d Wu, Yong; B. Schmittmann; R. K. P. Zia (2008). "Two-dimensional polymer networks near percolation". Journal of Physics A. 41 (2): 025008. Bibcode:2008JPhA...41b5004W. doi:10.1088/1751-8113/41/2/025004. S2CID 13053653.
- ^ a b c d e f g h i j k l m n o p q r s t u v w x y z aa ab ac ad Cornette, V.; A.J. Ramirez-Pastor, F. Nieto (2003). "Percolation of polyatomic species on a square lattice". European Physical Journal B. 36 (3): 391–399. Bibcode:2003EPJB...36..391C. doi:10.1140/epjb/e2003-00358-1. S2CID 119852589.
- ^ a b c Ziff, R. M.; C. R. Scullard; J. C. Wierman; M. R. A. Sedlock (2012). "The critical manifolds of inhomogeneous bond percolation on bow-tie and checkerboard lattices". Journal of Physics A. 45 (49): 494005. arXiv:1210.6609. Bibcode:2012JPhA...45W4005Z. doi:10.1088/1751-8113/45/49/494005. S2CID 2121370.
- ^ a b c d e f g h i j k Mertens, Stephan; Cristopher Moore (2012). "Continuum percolation thresholds in two dimensions". Physical Review E. 86 (6): 061109. arXiv:1209.4936. Bibcode:2012PhRvE..86f1109M. doi:10.1103/PhysRevE.86.061109. PMID 23367895. S2CID 15107275.
- ^ a b c d Quintanilla, John A.; R. M. Ziff (2007). "Asymmetry in the percolation thresholds of fully penetrable disks with two different radii". Physical Review E. 76 (5): 051115 [6 pages]. Bibcode:2007PhRvE..76e1115Q. doi:10.1103/PhysRevE.76.051115. PMID 18233631.
- ^ a b c Quintanilla, J; S. Torquato; R. M. Ziff (2000). "Efficient measurement of the percolation threshold for fully penetrable discs". J. Phys. A: Math. Gen. 33 (42): L399–L407. Bibcode:2000JPhA...33L.399Q. CiteSeerX 10.1.1.6.8207. doi:10.1088/0305-4470/33/42/104.
{{cite journal}}: CS1 maint : 복수이름 : 작성자 목록(링크) - ^ Lorenz, B; I. Orgzall and H.-O. Heuer (1993). "Universality and cluster structures in continuum models of percolation with two different radius distributions". J. Phys. A: Math. Gen. 26 (18): 4711–4712. Bibcode:1993JPhA...26.4711L. doi:10.1088/0305-4470/26/18/032.
- ^ Rosso, M (1989). "Concentration gradient approach to continuum percolation in two dimensions". J. Phys. A: Math. Gen. 22 (4): L131–L136. Bibcode:1989JPhA...22L.131R. doi:10.1088/0305-4470/22/4/004.
- ^ Gawlinski, Edward T; H. Eugene Stanley (1981). "Continuum percolation in two dimensions: Monte Carlo tests of scaling and universality for non-interacting discs". J. Phys. A: Math. Gen. 14 (8): L291–L299. Bibcode:1981JPhA...14L.291G. doi:10.1088/0305-4470/14/8/007.
- ^ a b c d e f g h i j k l m n o p q r Yi, Y.-B.; A. M. Sastry (2004). "Analytical approximation of the percolation threshold for overlapping ellipsoids of revolution". Proceedings of the Royal Society A. 460 (5): 2353–2380. Bibcode:2004RSPSA.460.2353Y. doi:10.1098/rspa.2004.1279. S2CID 2475482.
- ^ a b c Pike, G. E.; C. H. Seager (1974). "Percolation and conductivity: A computer study I". Phys. Rev. B. 10 (4): 1421–1434. Bibcode:1974PhRvB..10.1421P. doi:10.1103/PhysRevB.10.1421.
- ^ a b c d e f g h i j k Lin, Jianjun; Chen, Huisu (2019). "Measurement of continuum percolation properties of two-dimensional particulate systems comprising congruent and binary superellipses". Powder Technology. 347: 17–26. doi:10.1016/j.powtec.2019.02.036. S2CID 104332397.
- ^ Li, Mingqi; Chen, Huisu; Lin, Jianjun; Zhang, Rongling; Liu, Lin (July 2021). "Effects of the pore shape polydispersity on the percolation threshold and diffusivity of porous composites: Theoretical and numerical studies". Powder Technology. 386: 382–393. doi:10.1016/j.powtec.2021.03.055. ISSN 0032-5910. S2CID 233675695.
- ^ a b c d e f g h Charbonneau, Benoit; Patrick Charbonneau; Yi Hu; Zhen Yang (2021). "High-dimensional percolation criticality and hints of mean-field-like caging of the random Lorentz gas". Phys. Rev. E. 104 (2): 024137. arXiv:2105.04711. Bibcode:2021PhRvE.104b4137C. doi:10.1103/PhysRevE.104.024137. PMID 34525662. S2CID 234357912.
- ^ Domb, E. N. (1961). "Random Plane Networks". J. Soc. Indust. Appl. Math. 9 (4): 533–543. doi:10.1137/0109045.
- ^ Gilbert, E. N. (1961). "Random Plane Networks". J. Soc. Indust. Appl. Math. 9 (4): 533–543. doi:10.1137/0109045.
- ^ Xu, Wenhui; Junfeng Wang; Hao Hu; Youjin Deng (2021). "Critical polynomials in the nonplanar and continuum percolation models". Physical Review E. 103 (2): 022127. arXiv:2010.02887. Bibcode:2021PhRvE.103b2127X. doi:10.1103/PhysRevE.103.022127. ISSN 2470-0045. PMID 33736116. S2CID 222140792.
- ^ a b c Tarasevich, Yuri Yu.; Andrei V. Eserkepov (2020). "Percolation thresholds for discorectangles: numerical estimation for a range of aspect ratios". Physical Review E. 101 (2): 022108. arXiv:1910.05072. Bibcode:2020PhRvE.101b2108T. doi:10.1103/PhysRevE.101.022108. PMID 32168641. S2CID 204401814.
- ^ a b c d e f g h i j k l m n o p q r s Li, Jiantong; Mikael Östling (2016). "Precise percolation thresholds of two-dimensional random systems comprising overlapping ellipses". Physica A. 462: 940–950. Bibcode:2016PhyA..462..940L. doi:10.1016/j.physa.2016.06.020.
- ^ Nguyen, Van Lien; Enrique Canessa (1999). "Finite-size scaling in two-dimensional continuum percolation models". Modern Physics Letters B. 13 (17): 577–583. arXiv:cond-mat/9909200. Bibcode:1999MPLB...13..577N. doi:10.1142/S0217984999000737. S2CID 18560722.
- ^ Roberts, F. D. K. (1967). "A Monte Carlo Solution of a Two-Dimensional Unstructured Cluster Problem". Biometrika. 54 (3/4): 625–628. doi:10.2307/2335053. JSTOR 2335053. PMID 6064024.
- ^ a b c d e f g h i j k l m n o p q r s t u Xia, W.; M. F. Thorpe (1988). "Percolation properties of random ellipses". Physical Review A. 38 (5): 2650–2656. Bibcode:1988PhRvA..38.2650X. doi:10.1103/PhysRevA.38.2650. PMID 9900674.
- ^ a b c d e f g h i j k l m n o p q r s t u v w x y z Torquato, S.; Y. Jiao (2012). "Effect of dimensionality on the continuum percolation of overlapping hyperspheres and hypercubes. II. Simulation results and analyses". J. Chem. Phys. 137 (7): 074106. arXiv:1208.3720. Bibcode:2012JChPh.137g4106T. doi:10.1063/1.4742750. PMID 22920102. S2CID 13188197.
- ^ a b c d e f g h i j Baker, Don R.; Gerald Paul; Sameet Sreenivasan; H. Eugene Stanley (2002). "Continuum percolation threshold for interpenetrating squares and cubes". Physical Review E. 66 (4): 046136 [5 pages]. arXiv:cond-mat/0203235. Bibcode:2002PhRvE..66d6136B. doi:10.1103/PhysRevE.66.046136. PMID 12443288. S2CID 9561586.
- ^ a b c d e f g h i j k l m n Li, Jiantong; Mikael Östling (2013). "Percolation thresholds of two-dimensional continuum systems of rectangles". Physical Review E. 88 (1): 012101. Bibcode:2013PhRvE..88a2101L. doi:10.1103/PhysRevE.88.012101. PMID 23944408. S2CID 21438506.
- ^ Li, Jiantong; Shi-Li Zhang (2009). "Finite-size scaling in stick percolation". Physical Review E. 80 (4): 040104(R). Bibcode:2009PhRvE..80d0104L. doi:10.1103/PhysRevE.80.040104. PMID 19905260.
- ^ Tarasevich, Yuri Yu.; Andrei V. Eserkepov (2018). "Percolation of sticks: Effect of stick alignment and length dispersity". Physical Review E. 98 (6): 062142. arXiv:1811.06681. Bibcode:2018PhRvE..98f2142T. doi:10.1103/PhysRevE.98.062142. S2CID 54187951.
- ^ a b c d e f g h i Sasidevan, V. (2013). "Continuum percolation of overlapping discs with a distribution of radii having a power-law tail". Physical Review E. 88 (2): 022140. arXiv:1302.0085. Bibcode:2013PhRvE..88b2140S. doi:10.1103/PhysRevE.88.022140. PMID 24032808. S2CID 24046421.
- ^ a b van der Marck, S. C. (1996). "Network approach to void percolation in a pack of unequal spheres". Physical Review Letters. 77 (9): 1785–1788. Bibcode:1996PhRvL..77.1785V. doi:10.1103/PhysRevLett.77.1785. PMID 10063171.
- ^ a b c d e f g Jin, Yuliang; Patrick Charbonneau (2014). "Mapping the arrest of the random Lorentz gas onto the dynamical transition of a simple glass former". Physical Review E. 91 (4): 042313. arXiv:1409.0688. Bibcode:2015PhRvE..91d2313J. doi:10.1103/PhysRevE.91.042313. PMID 25974497. S2CID 16117644.
- ^ a b Lin, Jianjun; Zhang, Wulong; Chen, Huisu; Zhang, Rongling; Liu, Lin (2019). "Effect of pore characteristic on the percolation threshold and diffusivity of porous media comprising overlapping concave-shaped pores". International Journal of Heat and Mass Transfer. 138: 1333–1345. doi:10.1016/j.ijheatmasstransfer.2019.04.110. S2CID 164424008.
- ^ Meeks, Kelsey; J. Tencer; M.L. Pantoya (2017). "Percolation of binary disk systems: Modeling and theory". Phys. Rev. E. 95 (1): 012118. Bibcode:2017PhRvE..95a2118M. doi:10.1103/PhysRevE.95.012118. PMID 28208494.
- ^ Quintanilla, John A. (2001). "Measurement of the percolation threshold for fully penetrable disks of different radii". Phys. Rev. E. 63 (6): 061108. Bibcode:2001PhRvE..63f1108Q. doi:10.1103/PhysRevE.63.061108. PMID 11415069.
- ^ a b c Melchert, Oliver (2013). "Percolation thresholds on planar Euclidean relative-neighborhood graphs". Physical Review E. 87 (4): 042106. arXiv:1301.6967. Bibcode:2013PhRvE..87d2106M. doi:10.1103/PhysRevE.87.042106. PMID 23679372. S2CID 9691279.
- ^ a b Bernardi, Olivier; Curien, Nicolas; Miermont, Grėgory (2019). "A Boltzmann approach to percolation on random triangulations". Canadian Journal of Mathematics. 71: 1–43. arXiv:1705.04064. doi:10.4153/CJM-2018-009-x. S2CID 6817693.
- ^ a b c d e Becker, A.; R. M. Ziff (2009). "Percolation thresholds on two-dimensional Voronoi networks and Delaunay triangulations". Physical Review E. 80 (4): 041101. arXiv:0906.4360. Bibcode:2009PhRvE..80d1101B. doi:10.1103/PhysRevE.80.041101. PMID 19905267. S2CID 22549508.
- ^ Shante, K. S.; S. Kirkpatrick (1971). "An introduction to percolation theory". Advances in Physics. 20 (85): 325–357. Bibcode:1971AdPhy..20..325S. doi:10.1080/00018737100101261.
- ^ a b c Hsu, H. P.; M. C. Huang (1999). "Percolation thresholds, critical exponents, and scaling functions on planar random lattices and their duals". Physical Review E. 60 (6): 6361–6370. Bibcode:1999PhRvE..60.6361H. doi:10.1103/PhysRevE.60.6361. PMID 11970550. S2CID 8750738.
- ^ a b Huang, Ming-Chang; Hsiao-Ping Hsu (2002). "Percolation thresholds, critical exponents, and scaling functions on spherical random lattices". International Journal of Modern Physics C. 13 (3): 383–395. doi:10.1142/S012918310200319X.
- ^ a b Norrenbrock, C. (2014). "Percolation threshold on planar Euclidean Gabriel Graphs". Journal of Physics A. 40 (31): 9253–9258. arXiv:0704.2098. Bibcode:2007JPhA...40.9253P. doi:10.1088/1751-8113/40/31/005. S2CID 680787.
- ^ a b Bertin, E; J.-M. Billiot, R. Drouilhet (2002). "Continuum percolation in the Gabriel graph". Adv. Appl. Probab. 34 (4): 689. doi:10.1239/aap/1037990948. S2CID 121288601.
- ^ Lepage, Thibaut; Lucie Delaby; Fausto Malvagi; Alain Mazzolo (2011). "Monte Carlo simulation of fully Markovian stochastic geometries". Progress in Nuclear Science and Technology. 2: 743–748. doi:10.15669/pnst.2.743.
- ^ Zhang, C.; K. De'Bell (1993). "Reformulation of the percolation problem on a quasilattice: Estimates of the percolation threshold, chemical dimension, and amplitude ratio". Phys. Rev. B. 47 (14): 8558–8564. Bibcode:1993PhRvB..47.8558Z. doi:10.1103/PhysRevB.47.8558. PMID 10004894.
- ^ Ziff, R. M.; F. Babalievski (1999). "Site percolation on the Penrose rhomb lattice". Physica A. 269 (2–4): 201–210. Bibcode:1999PhyA..269..201Z. doi:10.1016/S0378-4371(99)00166-1.
- ^ Lu, Jian Ping; Joseph L. Birman (1987). "Percolation and Scaling on a Quasilattice". Journal of Statistical Physics. 46 (5/6): 1057–1066. Bibcode:1987JSP....46.1057L. doi:10.1007/BF01011156. S2CID 121645524.
- ^ a b c d e f g h Babalievski, F. (1995). "Percolation thresholds and percolation conductivities of octagonal and dodecagonal quasicrystalline lattices". Physica A. 220 (1995): 245–250. Bibcode:1995PhyA..220..245B. doi:10.1016/0378-4371(95)00260-E.
- ^ Bollobás, Béla; Oliver Riordan (2006). "The critical probability for random Voronoi percolation in the plane is 1/2". Probab. Theory Relat. Fields. 136 (3): 417–468. arXiv:math/0410336. doi:10.1007/s00440-005-0490-z. S2CID 15985691.
- ^ Angel, Omer; Schramm, Oded (2003). "Uniform infinite planar triangulation". Commun. Math. Phys. 241 (2–3): 191–213. arXiv:math/0207153. Bibcode:2003CMaPh.241..191A. doi:10.1007/s00220-003-0932-3. S2CID 17718301.
- ^ Angel, O.; Curien, Nicolas (2014). "Percolations on random maps I: Half-plane models". Annales de l'Institut Henri Poincaré, Probabilités et Statistiques. 51 (2): 405–431. arXiv:1301.5311. Bibcode:2015AIHPB..51..405A. doi:10.1214/13-AIHP583. S2CID 14964345.
- ^ a b c Zierenberg, Johannes; Niklas Fricke; Martin Marenz; F. P. Spitzner; Viktoria Blavatska; Wolfhard Janke (2017). "Percolation thresholds and fractal dimensions for square and cubic lattices with long-range correlated defects". Phys. Rev. E. 96 (6): 062125. arXiv:1708.02296. Bibcode:2017PhRvE..96f2125Z. doi:10.1103/PhysRevE.96.062125. PMID 29347311. S2CID 22353394.
- ^ a b c d e f g Sotta, P.; D. Long (2003). "The crossover from 2D to 3D percolation: Theory and numerical simulations". Eur. Phys. J. E. 11 (4): 375–388. Bibcode:2003EPJE...11..375S. doi:10.1140/epje/i2002-10161-6. PMID 15011039. S2CID 32831742.
- ^ a b c d e f g h i j k l m n o p q r s t u v w x y z aa ab Horton, M. K.; Moram, M. A. (April 17, 2017). "Alloy composition fluctuations and percolation in semiconductor alloy quantum wells". Applied Physics Letters. 110 (16): 162103. Bibcode:2017ApPhL.110p2103H. doi:10.1063/1.4980089. ISSN 0003-6951.
- ^ a b c d e f g Gliozzi, F.; S. Lottini; M. Panero; A. Rago (2005). "Random percolation as a gauge theory". Nuclear Physics B. 719 (3): 255–274. arXiv:cond-mat/0502339. Bibcode:2005NuPhB.719..255G. doi:10.1016/j.nuclphysb.2005.04.021. hdl:2318/5995. S2CID 119360708.
{{cite journal}}: CS1 maint : 복수이름 : 작성자 목록(링크) - ^ a b c d e f g h Yoo, Ted Y.; Jonathan Tran; Shane P. Stahlheber; Carina E. Kaainoa; Kevin Djepang; Alexander R. Small (2014). "Site percolation on lattices with low average coordination numbers". Journal of Statistical Mechanics: Theory and Experiment. 2014 (6): P06014. arXiv:1403.1676. Bibcode:2014JSMTE..06..014Y. doi:10.1088/1742-5468/2014/06/p06014. S2CID 119290405.
- ^ a b c d e f g h i j k Tran, Jonathan; Ted Yoo; Shane Stahlheber; Alex Small (2013). "Percolation thresholds on 3-dimensional lattices with 3 nearest neighbors". Journal of Statistical Mechanics: Theory and Experiment. 2013 (5): P05014. arXiv:1211.6531. Bibcode:2013JSMTE..05..014T. doi:10.1088/1742-5468/2013/05/P05014. S2CID 119182062.
- ^ Wells, A. F. (1984). "Structures Based on the 3-Connected Net 103 – b". Journal of Solid State Chemistry. 54 (3): 378–388. Bibcode:1984JSSCh..54..378W. doi:10.1016/0022-4596(84)90169-5.
- ^ a b Pant, Mihir; Don Towsley; Dirk Englund; Saikat Guha (2017). "Percolation thresholds for photonic quantum computing". Nature Communications. 10 (1): 1070. arXiv:1701.03775. doi:10.1038/s41467-019-08948-x. PMC 6403388. PMID 30842425.
- ^ Hyde, Stephen T.; O'Keeffe, Michael; Proserpio, Davide M. (2008). "A short history of an elusive yet ubiquitous structure in chemistry, materials, and mathematics". Angew. Chem. Int. Ed. 47 (42): 7996–8000. doi:10.1002/anie.200801519. PMID 18767088.
- ^ a b c d e f g h i j van der Marck, S. C. (1997). "Percolation thresholds of the duals of the face-centered-cubic, hexagonal-close-packed, and diamond lattices". Phys. Rev. E. 55 (6): 6593–6597. Bibcode:1997PhRvE..55.6593V. doi:10.1103/PhysRevE.55.6593.
- ^ a b Frisch, H. L.; E. Sonnenblick; V. A. Vyssotsky; J. M. Hammersley (1961). "Critical Percolation Probabilities (Site Problem)". Physical Review. 124 (4): 1021–1022. Bibcode:1961PhRv..124.1021F. doi:10.1103/PhysRev.124.1021.
{{cite journal}}: CS1 maint : 복수이름 : 작성자 목록(링크) - ^ a b Vyssotsky, V. A.; S. B. Gordon; H. L. Frisch; J. M. Hammersley (1961). "Critical Percolation Probabilities (Bond Problem)". Physical Review. 123 (5): 1566–1567. Bibcode:1961PhRv..123.1566V. doi:10.1103/PhysRev.123.1566.
{{cite journal}}: CS1 maint : 복수이름 : 작성자 목록(링크) - ^ a b c d e f g Gaunt, D. S.; M. F. Sykes (1983). "Series study of random percolation in three dimensions". J. Phys. A. 16 (4): 783. Bibcode:1983JPhA...16..783G. doi:10.1088/0305-4470/16/4/016.
- ^ a b c d Xu, Xiao; Junfeng Wang, Jian-Ping Lv, Youjin Deng (2014). "Simultaneous analysis of three-dimensional percolation models". Frontiers of Physics. 9 (1): 113–119. arXiv:1310.5399. Bibcode:2014FrPhy...9..113X. doi:10.1007/s11467-013-0403-z. S2CID 119250232.
{{cite journal}}: CS1 maint : 복수이름 : 작성자 목록(링크) - ^ Silverman, Amihal; J. Adler (1990). "Site-percolation threshold for a diamond lattice with diatomic substitution". Physical Review B. 42 (2): 1369–1373. Bibcode:1990PhRvB..42.1369S. doi:10.1103/PhysRevB.42.1369. PMID 9995550.
- ^ a b van der Marck, Steven C. (1997). "Erratum: Percolation thresholds and universal formulas". Phys. Rev. E. 56 (4): 3732.
- ^ a b c d e f g h i j k l m n o p q r s t van der Marck, Steven C. (1998). "Calculation of Percolation Thresholds in High Dimensions for FCC, BCC and Diamond Lattices". International Journal of Modern Physics C. 9 (4): 529–540. arXiv:cond-mat/9802187. Bibcode:1998IJMPC...9..529V. doi:10.1142/S0129183198000431. S2CID 119097158.
- ^ a b Sykes, M. F.; D. S. Gaunt; M. Glen (1976). "Percolation processes in three dimensions". J. Phys. A: Math. Gen. 9 (10): 1705–1712. Bibcode:1976JPhA....9.1705S. doi:10.1088/0305-4470/9/10/021.
- ^ a b c d e f g h Sykes, M. F.; J. W. Essam (1964). "Critical percolation probabilities by series method". Physical Review. 133 (1A): A310–A315. Bibcode:1964PhRv..133..310S. doi:10.1103/PhysRev.133.A310.
- ^ a b c d e f van der Marck, Steven C. (1998). "Site percolation and random walks on d-dimensional Kagome lattices". Journal of Physics A. 31 (15): 3449–3460. arXiv:cond-mat/9801112. Bibcode:1998JPhA...31.3449V. doi:10.1088/0305-4470/31/15/010. S2CID 18989583.
- ^ Sur, Amit; Joel L. Lebowitz; J. Marro; M. H. Kalos; S. Kirkpatrick (1976). "Monte Carlo studies of percolation phenomena for a simple cubic lattice". Journal of Statistical Physics. 15 (5): 345–353. Bibcode:1976JSP....15..345S. doi:10.1007/BF01020338. S2CID 38734613.
- ^ a b Wang, J; Z. Zhou; W. Zhang; T. Garoni; Y. Deng (2013). "Bond and site percolation in three dimensions". Physical Review E. 87 (5): 052107. arXiv:1302.0421. Bibcode:2013PhRvE..87e2107W. doi:10.1103/PhysRevE.87.052107. PMID 23767487. S2CID 14087496.
- ^ Grassberger, P. (1992). "Numerical studies of critical percolation in three dimensions". J. Phys. A. 25 (22): 5867–5888. Bibcode:1992JPhA...25.5867G. doi:10.1088/0305-4470/25/22/015.
- ^ Acharyya, M.; D. Stauffer (1998). "Effects of Boundary Conditions on the Critical Spanning Probability". Int. J. Mod. Phys. C. 9 (4): 643–647. arXiv:cond-mat/9805355. Bibcode:1998IJMPC...9..643A. doi:10.1142/S0129183198000534. S2CID 15684907.
- ^ Jan, N.; D. Stauffer (1998). "Random Site Percolation in Three Dimensions". Int. J. Mod. Phys. C. 9 (4): 341–347. Bibcode:1998IJMPC...9..341J. doi:10.1142/S0129183198000261.
- ^ Deng, Youjin; H. W. J. Blöte (2005). "Monte Carlo study of the site-percolation model in two and three dimensions". Physical Review E. 72 (1): 016126. Bibcode:2005PhRvE..72a6126D. doi:10.1103/PhysRevE.72.016126. PMID 16090055.
- ^ Ballesteros, P. N.; L. A. Fernández, V. Martín-Mayor, A. Muñoz, Sudepe, G. Parisi, and J. J. Ruiz-Lorenzo (1999). "Scaling corrections: site percolation and Ising model in three dimensions". Journal of Physics A. 32 (1): 1–13. arXiv:cond-mat/9805125. Bibcode:1999JPhA...32....1B. doi:10.1088/0305-4470/32/1/004. S2CID 2787294.
{{cite journal}}: CS1 maint : 복수이름 : 작성자 목록(링크) - ^ a b c Lorenz, C. D.; R. M. Ziff (1998). "Universality of the excess number of clusters and the crossing probability function in three-dimensional percolation". Journal of Physics A. 31 (40): 8147–8157. arXiv:cond-mat/9806224. Bibcode:1998JPhA...31.8147L. doi:10.1088/0305-4470/31/40/009. S2CID 12493873.
- ^ a b c d e f g h i j k Koza, Zbigniew; Jakub Poła (2016). "From discrete to continuous percolation in dimensions 3 to 7". Journal of Statistical Mechanics: Theory and Experiment. 2016 (10): 103206. arXiv:1606.08050. Bibcode:2016JSMTE..10.3206K. doi:10.1088/1742-5468/2016/10/103206. S2CID 118580056.
- ^ Škvor, Jiří; Ivo Nezbeda (2009). "Percolation threshold parameters of fluids". Physical Review E. 79 (4): 041141. Bibcode:2009PhRvE..79d1141S. doi:10.1103/PhysRevE.79.041141. PMID 19518207.
- ^ a b c d Adler, Joan; Yigal Meir; Amnon Aharony; A. B. Harris; Lior Klein (1990). "Low-Concentration Series in General Dimension". Journal of Statistical Physics. 58 (3/4): 511–538. Bibcode:1990JSP....58..511A. doi:10.1007/BF01112760. S2CID 122109020.
- ^ a b c d e f g h Dammer, Stephan M; Haye Hinrichsen (2004). "Spreading with immunization in high dimensions". Journal of Statistical Mechanics: Theory and Experiment. 2004 (7): P07011. arXiv:cond-mat/0405577. Bibcode:2004JSMTE..07..011D. doi:10.1088/1742-5468/2004/07/P07011. S2CID 118981083.
- ^ a b c Lorenz, C. D.; R. M. Ziff (1998). "Precise determination of the bond percolation thresholds and finite-size scaling corrections for the sc, fcc, and bcc lattices". Physical Review E. 57 (1): 230–236. arXiv:cond-mat/9710044. Bibcode:1998PhRvE..57..230L. doi:10.1103/PhysRevE.57.230. S2CID 119074750.
- ^ a b Schrenk, K. J.; N. A. M. Araújo; H. J. Herrmann (2013). "Stacked triangular lattice: percolation properties". Physical Review E. 87 (3): 032123. arXiv:1302.0484. Bibcode:2013PhRvE..87c2123S. doi:10.1103/PhysRevE.87.032123. S2CID 2917074.
- ^ Martins, P.; J. Plascak (2003). "Percolation on two- and three-dimensional lattices". Physical Review. 67 (4): 046119. arXiv:cond-mat/0304024. Bibcode:2003PhRvE..67d6119M. doi:10.1103/physreve.67.046119. PMID 12786448. S2CID 31891392.
- ^ Bradley, R. M.; P. N. Strenski, J.-M. Debierre (1991). "Surfaces of percolation clusters in three dimensions". Physical Review B. 44 (1): 76–84. Bibcode:1991PhRvB..44...76B. doi:10.1103/PhysRevB.44.76. PMID 9998221.
- ^ a b c d e f Kurzawski, Ł.; K. Malarz (2012). "Simple cubic random-site percolation thresholds for complex neighbourhoods". Rep. Math. Phys. 70 (2): 163–169. arXiv:1111.3254. Bibcode:2012RpMP...70..163K. CiteSeerX 10.1.1.743.1726. doi:10.1016/S0034-4877(12)60036-6. S2CID 119120046.
- ^ Gallyamov, S. R.; S.A. Melchukov (2013). "Percolation threshold of a simple cubic lattice with fourth neighbors: the theory and numerical calculation with parallelization" (PDF). Third International Conference "High Performance Computing" HPC-UA 2013 (Ukraine, Kyiv, October 7–11, 2013).
- ^ Sykes, M. F.; D. S. Gaunt; J. W. Essam (1976). "The percolation probability for the site problem on the face-centred cubic lattice". Journal of Physics A. 9 (5): L43–L46. Bibcode:1976JPhA....9L..43S. doi:10.1088/0305-4470/9/5/002.
- ^ a b c d e f g h i j k l m n o p q r s t u v w x y z aa ab ac ad ae af ag ah Hu, Yi; Patrick Charbonneau (2021). "Percolation thresholds on high-dimensional Dn and E8-related lattices". Physical Review E. 103 (6): 062115. arXiv:2102.09682. Bibcode:2021PhRvE.103f2115H. doi:10.1103/PhysRevE.103.062115. PMID 34271715. S2CID 231979212.
- ^ a b Lorenz, C. D.; R. May; R. M. Ziff (2000). "Similarity of Percolation Thresholds on the HCP and FCC Lattices" (PDF). Journal of Statistical Physics. 98 (3/4): 961–970. doi:10.1023/A:1018648130343. hdl:2027.42/45178. S2CID 10950378.
- ^ Tahir-Kheli, Jamil; W. A. Goddard III (2007). "Chiral plaquette polaron theory of cuprate superconductivity". Physical Review B. 76 (1): 014514. arXiv:0707.3535. Bibcode:2007PhRvB..76a4514T. doi:10.1103/PhysRevB.76.014514. S2CID 8882419.
- ^ a b c d e f g Malarz, Krzysztof (2015). "Simple cubic random-site percolation thresholds for neighborhoods containing fourth-nearest neighbors". Phys. Rev. E. 91 (4): 043301. arXiv:1501.01586. Bibcode:2015PhRvE..91d3301M. doi:10.1103/PhysRevE.91.043301. PMID 25974606. S2CID 37943657.
- ^ a b c d e f g h i j Xun, Zhipeng; Robert M. Ziff (2020). "Bond percolation on simple cubic lattices with extended neighborhoods". Phys. Rev. E. 102 (4): 012102. arXiv:2001.00349. Bibcode:2020PhRvE.102a2102X. doi:10.1103/PhysRevE.102.012102. PMID 32795057. S2CID 209531616.
- ^ a b c d Jerauld, G. R.; L. E. Scriven; H. T. Davis (1984). "Percolation and conduction on the 3D Voronoi and regular networks: a second case study in topological disorder". J. Phys. C: Solid State Phys. 17 (19): 3429–3439. Bibcode:1984JPhC...17.3429J. doi:10.1088/0022-3719/17/19/017.
- ^ Xu, Fangbo; Zhiping Xu; Boris I. Yakobson (2014). "Site-Percolation Threshold of Carbon Nanotube Fibers---Fast Inspection of Percolation with Markov Stochastic Theory". Physica A. 407: 341–349. arXiv:1401.2130. Bibcode:2014PhyA..407..341X. doi:10.1016/j.physa.2014.04.013. S2CID 119267606.
- ^ a b c Gawron, T. R.; Marek Cieplak (1991). "Site percolation thresholds of the FCC lattice" (PDF). Acta Physica Polonica A. 80 (3): 461. Bibcode:1991AcPPA..80..461G. doi:10.12693/APhysPolA.80.461.
- ^ Harter, T. (2005). "Finite-size scaling analysis of percolation in three-dimensional correlated binary Markov chain random fields". Physical Review E. 72 (2): 026120. Bibcode:2005PhRvE..72b6120H. doi:10.1103/PhysRevE.72.026120. PMID 16196657. S2CID 2708506.
- ^ Sykes, M. F.; J. J. Rehr; Maureen Glen (1996). "A note on the percolation probabilities of pairs of closely similar lattices". Proc. Camb. Phil. Soc. 76: 389–392. doi:10.1017/S0305004100049021.
- ^ Weber, H.; W. Paul (1996). "Penetrant diffusion in frozen polymer matrices: A finite-size scaling study of free volume percolation". Physical Review E. 54 (4): 3999–4007. Bibcode:1996PhRvE..54.3999W. doi:10.1103/PhysRevE.54.3999. PMID 9965547.
- ^ Tarasevich, Yu. Yu.; V. A. Cherkasova (2007). "Dimer percolation and jamming on simple cubic lattice". European Physical Journal B. 60 (1): 97–100. arXiv:0709.3626. Bibcode:2007EPJB...60...97T. doi:10.1140/epjb/e2007-00321-2. S2CID 5419806.
- ^ Holcomb, D F..; J. J. Rehr, Jr. (1969). "Percolation in heavily doped semiconductors*". Physical Review. 183 (3): 773–776. Bibcode:1969PhRv..183..773H. doi:10.1103/PhysRev.183.773.
- ^ Holcomb, D F.; F. Holcomb; M. Iwasawa (1972). "Clustering of randomly placed spheres". Biometrika. 59: 207–209. doi:10.1093/biomet/59.1.207.
- ^ Shante, Vinod K. S.; Scott Kirkpatrick (1971). "An introduction to percolation theory". Advances in Physics. 20 (85): 325–357. doi:10.1080/00018737100101261.
- ^ a b Rintoul, M. D.; S. Torquato (1997). "Precise determination of the critical threshold and exponents in a three-dimensional continuum percolation model". J. Phys. A: Math. Gen. 30 (16): L585. Bibcode:1997JPhA...30L.585R. CiteSeerX 10.1.1.42.4284. doi:10.1088/0305-4470/30/16/005.
- ^ Consiglio, R.; R. Baker; G. Paul; H. E. Stanley (2003). "Continuum percolation of congruent overlapping spherocylinders". Physica A. 319: 49–55. doi:10.1016/S0378-4371(02)01501-7.
- ^ a b c d e f g h Xu, Wenxiang; Xianglong Su; Yang Jiao (2016). "Continuum percolation of congruent overlapping spherocylinders". Phys. Rev. E. 93 (3): 032122. Bibcode:2016PhRvE..94c2122X. doi:10.1103/PhysRevE.94.032122. PMID 27078307.
- ^ a b Lorenz, C. D.; R. M. Ziff (2000). "Precise determination of the critical percolation threshold for the three dimensional Swiss cheese model using a growth algorithm" (PDF). J. Chem. Phys. 114 (8): 3659. Bibcode:2001JChPh.114.3659L. doi:10.1063/1.1338506. hdl:2027.42/70114.
- ^ a b c d e f g h i Lin, Jianjun; Chen, Huisu; Xu, Wenxiang (2018). "Geometrical percolation threshold of congruent cuboidlike particles in overlapping particle systems". Physical Review E. 98 (1): 012134. Bibcode:2018PhRvE..98a2134L. doi:10.1103/PhysRevE.98.012134. PMID 30110832. S2CID 52017287.
- ^ a b c d e f g h i j k l m n o p q r s t u v w x y z aa ab ac ad ae af ag ah ai Garboczi, E. J.; K. A. Snyder; J. F. Douglas (1995). "Geometrical percolation threshold of overlapping ellipsoids". Phys. Rev. E. 52 (1): 819–827. Bibcode:1995PhRvE..52..819G. doi:10.1103/PhysRevE.52.819. PMID 9963485.
- ^ a b c d Li, Mingqi; Chen, Huisu; Lin, Jianjun (January 2020). "Efficient measurement of the percolation threshold for random systems of congruent overlapping ovoids". Powder Technology. 360: 598–607. doi:10.1016/j.powtec.2019.10.044. ISSN 0032-5910. S2CID 208693526.
- ^ Li, Mingqi; Chen, Huisu; Lin, Jianjun (April 2020). "Numerical study for the percolation threshold and transport properties of porous composites comprising non-centrosymmetrical superovoidal pores". Computer Methods in Applied Mechanics and Engineering. 361: 112815. Bibcode:2020CMAME.361k2815L. doi:10.1016/j.cma.2019.112815. ISSN 0045-7825. S2CID 213152892.
- ^ Gori, Giacomo; Andrea Trombettoni (2015). "Conformal invariance in three dimensional percolation". Journal of Statistical Mechanics: Theory and Experiment. 2015 (7): P07014. arXiv:1504.07209. Bibcode:2015JSMTE..07..014G. doi:10.1088/1742-5468/2015/07/P07014. S2CID 119292052.
- ^ a b c d e f g h i j Yi, Y.-B.; A. M. Sastry (2004). "Analytical approximation of the percolation threshold for overlapping ellipsoids of revolution". Proc. R. Soc. Lond. A. 460 (2048): 2353–2380. Bibcode:2004RSPSA.460.2353Y. doi:10.1098/rspa.2004.1279. S2CID 2475482.
- ^ a b c Hyytiä, E.; J. Virtamo, P. Lassila and J. Ott (2012). "Continuum percolation threshold for permeable aligned cylinders and opportunistic networking". IEEE Communications Letters. 16 (7): 1064–1067. doi:10.1109/LCOMM.2012.051512.120497. S2CID 1056865.
- ^ a b c d e Torquato, S.; Y. Jiao (2012). "Effect of Dimensionality on the Percolation Threshold of Overlapping Nonspherical Hyperparticles". Physical Review E. 87 (2): 022111. arXiv:1210.0134. Bibcode:2013PhRvE..87b2111T. doi:10.1103/PhysRevE.87.022111. PMID 23496464. S2CID 11417012.
- ^ a b c Yi, Y. B.; E. Tawerghi (2009). "Geometric percolation thresholds of interpenetrating plates in three-dimensional space". Physical Review E. 79 (4): 041134. Bibcode:2009PhRvE..79d1134Y. doi:10.1103/PhysRevE.79.041134. PMID 19518200.
- ^ a b c d e Yi, Y. B.; K. Esmail (2012). "Computational measurement of void percolation thresholds of oblate particles and thin plate composites". J. Appl. Phys. 111 (12): 124903. Bibcode:2012JAP...111l4903Y. doi:10.1063/1.4730333.
- ^ a b Priour, Jr., D. J.; N. J. McGuigan (2017). "Percolation through voids around randomly oriented faceted inclusions". arXiv:1712.10241 [cond-mat.stat-mech].
- ^ a b c d e f g h i j k Priour, Jr., D. J.; N. J. McGuigan (2018). "Percolation through voids around randomly oriented polyhedra and axially symmetric grains". Phys. Rev. Lett. 121 (22): 225701. arXiv:1801.09970. Bibcode:2018PhRvL.121v5701P. doi:10.1103/PhysRevLett.121.225701. PMID 30547614. S2CID 119185480.
- ^ Kertesz, Janos (1981). "Percolation of holes between overlapping spheres: Monte Carlo calculation of the critical volume fraction" (PDF). Journal de Physique Lettres. 42 (17): L393–L395. doi:10.1051/jphyslet:019810042017039300.
- ^ Elam, W. T.; A. R. Kerstein; J. J. Rehr (1984). "Critical properties of the void percolation problem for spheres". Phys. Rev. Lett. 52 (7): 1516–1519. Bibcode:1984PhRvL..52.1516E. doi:10.1103/PhysRevLett.52.1516.
- ^ Rintoul, M. D. (2000). "Precise determination of the void percolation threshold for two distributions of overlapping spheres". Physical Review E. 62 (6): 68–72. Bibcode:2000PhRvE..62...68R. doi:10.1103/PhysRevE.62.68. PMID 11088435.
- ^ Yi, Y. B. (2006). "Void percolation and conduction of overlapping ellipsoids". Physical Review E. 74 (3): 031112. Bibcode:2006PhRvE..74c1112Y. doi:10.1103/PhysRevE.74.031112. PMID 17025599.
- ^ a b Höfling, F.; T. Munk; E. Frey; T. Franosch (2008). "Critical dynamics of ballistic and Brownian particles in a heterogeneous environment". J. Chem. Phys. 128 (16): 164517. arXiv:0712.2313. Bibcode:2008JChPh.128p4517H. doi:10.1063/1.2901170. PMID 18447469. S2CID 25509814.
- ^ Priour, Jr., D.J. (2014). "Percolation through voids around overlapping spheres: A dynamically based finite-size scaling analysis". Phys. Rev. E. 89 (1): 012148. arXiv:1208.0328. Bibcode:2014PhRvE..89a2148P. doi:10.1103/PhysRevE.89.012148. PMID 24580213. S2CID 20349307.
- ^ a b c Powell, M. J. (1979). "Site percolation in randomly packed spheres". Physical Review B. 20 (10): 4194–4198. Bibcode:1979PhRvB..20.4194P. doi:10.1103/PhysRevB.20.4194.
- ^ a b Ziff, R. M.; Salvatore Torquato (2016). "Percolation of disordered jammed sphere packings". Journal of Physics A: Mathematical and Theoretical. 50 (8): 085001. arXiv:1611.00279. Bibcode:2017JPhA...50h5001Z. doi:10.1088/1751-8121/aa5664. S2CID 53003822.
- ^ Lin, Jianjun; Chen, Huisu (2018). "Continuum percolation of porous media via random packing of overlapping cube-like particles". Theoretical & Applied Mechanics Letters. 8 (5): 299–303. doi:10.1016/j.taml.2018.05.007.
- ^ Lin, Jianjun; Chen, Huisu (2018). "Effect of particle morphologies on the percolation of particulate porous media: A study of superballs". Powder Technology. 335: 388–400. doi:10.1016/j.powtec.2018.05.015. S2CID 103471554.
- ^ Clerc, J. P.; G. Giraud; S. Alexander; E. Guyon (1979). "Conductivity of a mixture of conducting and insulating grains: Dimensionality effects". Physical Review B. 22 (5): 2489–2494. doi:10.1103/PhysRevB.22.2489.
- ^ C. Larmier, E. Dumonteil, F. Malvagi, A. Mazzolo, and A. Zoia, C (2016). "Finite-size effects and percolation properties of Poisson geometries". Physical Review E. 94 (1): 012130. arXiv:1605.04550. Bibcode:2016PhRvE..94a2130L. doi:10.1103/PhysRevE.94.012130. PMID 27575099. S2CID 19361619.
{{cite journal}}: CS1 maint : 복수이름 : 작성자 목록(링크) - ^ a b c d e f Zakalyukin, R. M.; V. A. Chizhikov (2005). "Calculations of the Percolation Thresholds of a Three-Dimensional (Icosahedral) Penrose Tiling by the Cubic Approximant Method". Crystallography Reports. 50 (6): 938–948. Bibcode:2005CryRp..50..938Z. doi:10.1134/1.2132400. S2CID 94290876.
- ^ Kantor, Yacov (1986). "Three-dimensional percolation with removed lines of sites". Phys. Rev. B. 33 (5): 3522–3525. Bibcode:1986PhRvB..33.3522K. doi:10.1103/PhysRevB.33.3522. PMID 9938740.
- ^ Schrenk, K. J.; M. R. Hilário; V. Sidoravicius; N. A. M. Araújo; H. J. Herrmann; M. Thielmann; A. Teixeira (2016). "Critical Fragmentation Properties of Random Drilling: How Many Holes Need to Be Drilled to Collapse a Wooden Cube?". Phys. Rev. Lett. 116 (5): 055701. arXiv:1601.03534. Bibcode:2016PhRvL.116e5701S. doi:10.1103/PhysRevLett.116.055701. PMID 26894717. S2CID 3145131.
- ^ Grassberger, P. (2017). "Some remarks on drilling percolation". Phys. Rev. E. 95 (1): 010103. arXiv:1611.07939. doi:10.1103/PhysRevE.95.010103. PMID 28208497. S2CID 12476714.
- ^ a b Szczygieł, Bartłomiej; Kamil Kwiatkowski; Maciej Lewenstein; Gerald John Lapeyre, Jr.; Jan Wehr (2016). "Percolation thresholds for discrete-continuous models with nonuniform probabilities of bond formation". Phys. Rev. E. 93 (2): 022127. arXiv:1509.07401. Bibcode:2016PhRvE..93b2127S. doi:10.1103/PhysRevE.93.022127. PMID 26986308. S2CID 18110437.
- ^ a b c Kirkpatrick, Scott (1976). "Percolation phenomena in higher dimensions: Approach to the mean-field limit". Physical Review Letters. 36 (2): 69–72. Bibcode:1976PhRvL..36...69K. doi:10.1103/PhysRevLett.36.69.
- ^ a b c d Gaunt, D. S.; Sykes, M. F.; Ruskin, Heather (1976). "Percolation processes in d-dimensions". J. Phys. A: Math. Gen. 9 (11): 1899–1911. Bibcode:1976JPhA....9.1899G. doi:10.1088/0305-4470/9/11/015.
- ^ a b c d e f g h i j k l m n o p q r s t Grassberger, Peter (2003). "Critical percolation in high dimensions". Physical Review E. 67 (3): 4. arXiv:cond-mat/0202144. Bibcode:2003PhRvE..67c6101G. doi:10.1103/PhysRevE.67.036101. PMID 12689126. S2CID 43707822.
- ^ a b Paul, Gerald; Robert M. Ziff; H. Eugene Stanley (2001). "Percolation threshold, Fisher exponent, and shortest path exponent for four and five dimensions". Physical Review E. 64 (2): 8. arXiv:cond-mat/0101136. Bibcode:2001PhRvE..64b6115P. doi:10.1103/PhysRevE.64.026115. PMID 11497659. S2CID 18271196.
- ^ Ballesteros, H. G.; L. A. Fernández; V. Martín-Mayor; A. Muñoz Sudupe; G. Parisi; J. J. Ruiz-Lorenzo (1997). "Measures of critical exponents in the four dimensional site percolation". Phys. Lett. B. 400 (3–4): 346–351. arXiv:hep-lat/9612024. Bibcode:1997PhLB..400..346B. doi:10.1016/S0370-2693(97)00337-7. S2CID 10242417.
- ^ a b c d e f g Kotwica, M.; P. Gronek; K. Malarz (2019). "Efficient space virtualisation for Hoshen–Kopelman algorithm". International Journal of Modern Physics C. 30: 1950055. arXiv:1803.09504. Bibcode:2018arXiv180309504K. doi:10.1142/S0129183119500554. S2CID 4418563.
- ^ a b c d e f g h i j k l m n o p q r s t Mertens, Stephan; Christopher Moore (2018). "Percolation Thresholds and Fisher Exponents in Hypercubic Lattices". Phys. Rev. E. 98 (2): 022120. arXiv:1806.08067. Bibcode:2018PhRvE..98b2120M. doi:10.1103/PhysRevE.98.022120. PMID 30253462. S2CID 52821851.
- ^ a b c d Xun, Zhipeng (2020). "Precise bond percolation thresholds on several four-dimensional lattices". Physical Review Research. 2 (1): 013067. arXiv:1910.11408. Bibcode:2020PhRvR...2a3067X. doi:10.1103/PhysRevResearch.2.013067. S2CID 204915841.
- ^ a b c d e Adler, Joan; Yigal Meir; Amnon Aharony; A. B. Harris (1990). "Series Study of Percolation Moments in General Dimension". Physical Review B. 41 (13): 9183–9206. Bibcode:1990PhRvB..41.9183A. doi:10.1103/PhysRevB.41.9183. PMID 9993262.
- ^ Stauffer, Dietrich; Robert M. Ziff (1999). "Reexamination of Seven-Dimensional Site Percolation Thresholds". International Journal of Modern Physics C. 11 (1): 205–209. arXiv:cond-mat/9911090. Bibcode:2000IJMPC..11..205S. doi:10.1142/S0129183100000183. S2CID 119362011.
- ^ Gaunt, D. S.; Ruskin, Heather (1978). "Bond percolation processes in d-dimensions". J. Phys. A: Math. Gen. 11 (7): 1369. Bibcode:1978JPhA...11.1369G. doi:10.1088/0305-4470/11/7/025.
- ^ Mertens, Stephan; Christopher Moore (2018). "Series Expansion of Critical Densities for Percolation on ℤd". J. Phys. A: Math. Theor. 51 (47): 475001. arXiv:1805.02701. doi:10.1088/1751-8121/aae65c. S2CID 119399128.
- ^ a b Gori, G.; Michelangeli, M.; Defenu, N.; Trombettoni, A. (2017). "One-dimensional long-range percolation: A numerical study". Physical Review E. 96 (1): 012108. arXiv:1610.00200. Bibcode:2017PhRvE..96a2108G. doi:10.1103/physreve.96.012108. PMID 29347133. S2CID 9926800.
- ^ a b Schulman, L. S. (1983). "Long range percolation in one dimension". Journal of Physics A: Mathematical and General. 16 (17): L639–L641. Bibcode:1983JPhA...16L.639S. doi:10.1088/0305-4470/16/17/001. ISSN 0305-4470.
- ^ Aizenman, M.; Newman, C. M. (December 1, 1986). "Discontinuity of the percolation density in one dimensional 1/ x−y 2 percolation models". Communications in Mathematical Physics. 107 (4): 611–647. Bibcode:1986CMaPh.107..611A. doi:10.1007/BF01205489. ISSN 0010-3616. S2CID 117904292.
- ^ Baek, S.K.; Petter Minnhagen and Beom Jun Kim (2009). "Comment on 'Monte Carlo simulation study of the two-stage percolation transition in enhanced binary trees'". J. Phys. A: Math. Theor. 42 (47): 478001. arXiv:0910.4340. Bibcode:2009JPhA...42U8001B. doi:10.1088/1751-8113/42/47/478001. S2CID 102489139.
- ^ a b c Boettcher, Stefan; Jessica L. Cook and Robert M. Ziff (2009). "Patchy percolation on a hierarchical network with small-world bonds". Phys. Rev. E. 80 (4): 041115. arXiv:0907.2717. Bibcode:2009PhRvE..80d1115B. doi:10.1103/PhysRevE.80.041115. PMID 19905281.
- ^ a b c d e f g h i j k l m n o p q r s t u v w x y z aa ab ac ad ae af ag ah ai aj ak al am an Mertens, Stephan; Cristopher Moore (2017). "Percolation thresholds in hyperbolic lattices". Phys. Rev. E. 96 (4): 042116. arXiv:1708.05876. Bibcode:2017PhRvE..96d2116M. doi:10.1103/PhysRevE.96.042116. PMID 29347529. S2CID 39025690.
- ^ a b c Lopez, Jorge H.; J. M. Schwarz (2017). "Constraint percolation on hyperbolic lattices". Phys. Rev. E. 96 (5): 052108. arXiv:1512.05404. Bibcode:2017PhRvE..96e2108L. doi:10.1103/PhysRevE.96.052108. PMID 29347694. S2CID 44770310.
- ^ a b c d e f g h i Baek, S.K.; Petter Minnhagen and Beom Jun Kim (2009). "Percolation on hyperbolic lattices". Phys. Rev. E. 79 (1): 011124. arXiv:0901.0483. Bibcode:2009PhRvE..79a1124B. doi:10.1103/PhysRevE.79.011124. PMID 19257018. S2CID 29468086.
- ^ a b c d e f g h Gu, Hang; Robert M. Ziff (2012). "Crossing on hyperbolic lattices". Phys. Rev. E. 85 (5): 051141. arXiv:1111.5626. Bibcode:2012PhRvE..85e1141G. doi:10.1103/PhysRevE.85.051141. PMID 23004737. S2CID 7141649.
- ^ a b c d Nogawa, Tomoaki; Takehisa Hasegawa (2009). "Monte Carlo simulation study of the two-stage percolation transition in enhanced binary trees". J. Phys. A: Math. Theor. 42 (14): 145001. arXiv:0810.1602. Bibcode:2009JPhA...42n5001N. doi:10.1088/1751-8113/42/14/145001. S2CID 118367190.
- ^ a b Minnhagen, Petter; Seung Ki Baek (2010). "Analytic results for the percolation transitions of the enhanced binary tree". Phys. Rev. E. 82 (1): 011113. arXiv:1003.6012. Bibcode:2010PhRvE..82a1113M. doi:10.1103/PhysRevE.82.011113. PMID 20866571. S2CID 21018113.
- ^ Kozáková, Iva (2009). "Critical percolation of virtually free groups and other tree-like graphs". Annals of Probability. 37 (6): 2262–2296. arXiv:0801.4153. doi:10.1214/09-AOP458.
- ^ Cohen, R; K. Erez; D. Ben-Avraham; S. Havlin (2000). "Resilience of the Internet to random breakdowns". Phys. Rev. Lett. 85 (21): 4626–8. arXiv:cond-mat/0007048. Bibcode:2000PhRvL..85.4626C. CiteSeerX 10.1.1.242.6797. doi:10.1103/PhysRevLett.85.4626. PMID 11082612. S2CID 15372152.
- ^ a b c d e f g h i j k l m n o p q r s t u v w x y z aa ab ac ad ae af ag ah Wang, Junfeng; Zongzheng Zhou; Qingquan Liu; Timothy M. Garoni; Youjin Deng (2013). "A high-precision Monte Carlo study of directed percolation in (d + 1) dimensions". Physical Review E. 88 (4): 042102. arXiv:1201.3006. Bibcode:2013PhRvE..88d2102W. doi:10.1103/PhysRevE.88.042102. PMID 24229111. S2CID 43011467.
- ^ a b Jensen, Iwan; Anthony J. Guttmann (1995). "Series expansions of the percolation probability for directed square and honeycomb lattices". J. Phys. A: Math. Gen. 28 (17): 4813–4833. arXiv:cond-mat/9509121. Bibcode:1995JPhA...28.4813J. doi:10.1088/0305-4470/28/17/015. S2CID 118993303.
- ^ a b Jensen, Iwan (2004). "Low-density series expansions for directed percolation: III. Some two-dimensional lattices". J. Phys. A: Math. Gen. 37 (4): 6899–6915. arXiv:cond-mat/0405504. Bibcode:2004JPhA...37.6899J. CiteSeerX 10.1.1.700.2691. doi:10.1088/0305-4470/37/27/003. S2CID 119326380.
- ^ a b c d Essam, J. W.; A. J. Guttmann; K. De'Bell (1988). "On two-dimensional directed percolation". J. Phys. A. 21 (19): 3815–3832. Bibcode:1988JPhA...21.3815E. doi:10.1088/0305-4470/21/19/018.
- ^ Lübeck, S.; R. D. Willmann (2002). "Universal scaling behaviour of directed percolation and the pair contact process in an external field". J. Phys. A. 35 (48): 10205. arXiv:cond-mat/0210403. Bibcode:2002JPhA...3510205L. doi:10.1088/0305-4470/35/48/301. S2CID 11831269.
- ^ a b Jensen, Iwan (1999). "Low-density series expansions for directed percolation: I. A new efficient algorithm with applications to the square lattice". J. Phys. A. 32 (28): 5233–5249. arXiv:cond-mat/9906036. Bibcode:1999JPhA...32.5233J. doi:10.1088/0305-4470/32/28/304. S2CID 2681356.
- ^ Essam, John; K. De'Bell; J. Adler; F. M. Bhatti (1986). "Analysis of extended series for bond percolation on the directed square lattice". Physical Review B. 33 (2): 1982–1986. Bibcode:1986PhRvB..33.1982E. doi:10.1103/PhysRevB.33.1982. PMID 9938508.
- ^ Baxter, R. J.; A. J. Guttmann (1988). "Series expansion of the percolation probability for the directed square lattice". J. Phys. A. 21 (15): 3193–3204. Bibcode:1988JPhA...21.3193B. doi:10.1088/0305-4470/21/15/008.
- ^ a b c Jensen, Iwan (1996). "Low-density series expansions for directed percolation on square and triangular lattices". J. Phys. A. 29 (22): 7013–7040. Bibcode:1996JPhA...29.7013J. doi:10.1088/0305-4470/29/22/007. S2CID 121332666.
- ^ a b c d e f g h i j Blease, J. (1977). "Series expansions for the directed-bond percolation problem". J. Phys. C: Solid State Phys. 10 (7): 917–924. Bibcode:1977JPhC...10..917B. doi:10.1088/0022-3719/10/7/003.
- ^ a b c Grassberger, P.; Y.-C. Zhang (1996). ""Self-organized" formulation of standard percolation phenomena". Physica A. 224 (1): 169–179. Bibcode:1996PhyA..224..169G. doi:10.1016/0378-4371(95)00321-5.
- ^ a b c d e f Grassberger, P. (2009). "Local persistence in directed percolation". Journal of Statistical Mechanics: Theory and Experiment. 2009 (8): P08021. arXiv:0907.4021. Bibcode:2009JSMTE..08..021G. doi:10.1088/1742-5468/2009/08/P08021. S2CID 119236556.
- ^ a b c d Lübeck, S.; R. D. Willmann (2004). "Universal scaling behavior of directed percolation around the upper critical dimension". J. Stat. Phys. 115 (5–6): 1231–1250. arXiv:cond-mat/0401395. Bibcode:2004JSP...115.1231L. CiteSeerX 10.1.1.310.8700. doi:10.1023/B:JOSS.0000028059.24904.3b. S2CID 16267627.
- ^ Perlsman, E.; S. Havlin (2002). "Method to estimate critical exponents using numerical studies". Europhys. Lett. 58 (2): 176–181. Bibcode:2002EL.....58..176P. doi:10.1209/epl/i2002-00621-7. S2CID 67818664.
- ^ Adler, Joan; J. Berger, M. A. M. S. Duarte, Y. Meir (1988). "Directed percolation in 3+1 dimensions". Physical Review B. 37 (13): 7529–7533. Bibcode:1988PhRvB..37.7529A. doi:10.1103/PhysRevB.37.7529. PMID 9944046.
{{cite journal}}: CS1 maint : 복수이름 : 작성자 목록(링크) - ^ a b Grassberger, Peter (2009). "Logarithmic corrections in (4 + 1)-dimensional directed percolation". Physical Review E. 79 (5): 052104. arXiv:0904.0804. Bibcode:2009PhRvE..79e2104G. doi:10.1103/PhysRevE.79.052104. PMID 19518501. S2CID 23876626.
- ^ Wu, F. Y. (2010). "Critical frontier of the Potts and percolation models on triangular-type and kagome-type lattices I: Closed-form expressions". Physical Review E. 81 (6): 061110. arXiv:0911.2514. Bibcode:2010PhRvE..81f1110W. doi:10.1103/PhysRevE.81.061110. PMID 20866381. S2CID 31590247.
- ^ Damavandi, Ojan Khatib; Robert M. Ziff (2015). "Percolation on hypergraphs with four-edges". J. Phys. A: Math. Theor. 48 (40): 405004. arXiv:1506.06125. Bibcode:2015JPhA...48N5004K. doi:10.1088/1751-8113/48/40/405004. S2CID 118481075.
- ^ a b Wu, F. Y. (2006). "New Critical Frontiers for the Potts and Percolation Models". Physical Review Letters. 96 (9): 090602. arXiv:cond-mat/0601150. Bibcode:2006PhRvL..96i0602W. CiteSeerX 10.1.1.241.6346. doi:10.1103/PhysRevLett.96.090602. PMID 16606250. S2CID 15182833.
- ^ Reuven Cohen; Shlomo Havlin (2010). Complex Networks: Structure, Robustness and Function. Cambridge University Press.
- ^ S. V. Buldyrev; R. Parshani; G. Paul; H. E. Stanley; S. Havlin (2010). "Catastrophic cascade of failures in interdependent networks". Nature. 464 (7291): 1025–28. arXiv:0907.1182. Bibcode:2010Natur.464.1025B. doi:10.1038/nature08932. PMID 20393559. S2CID 1836955.
- ^ Gao, Jianxi; Buldyrev, Sergey V.; Stanley, H. Eugene; Havlin, Shlomo (2011). "Networks formed from interdependent networks". Nature Physics. 8 (1): 40–48. Bibcode:2012NatPh...8...40G. CiteSeerX 10.1.1.379.8214. doi:10.1038/nphys2180. ISSN 1745-2473.










 유사한
유사한






![{\displaystyle p_{b}p_{s}[1-({\sqrt {p_{bc}}}/(3-p_{bc}))({\sqrt {p_{b}}}-{\sqrt {p_{bc}}})]=p_{bc}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/841ca3acd9efa5a314d4308e4cae70eacb5fd1e5)

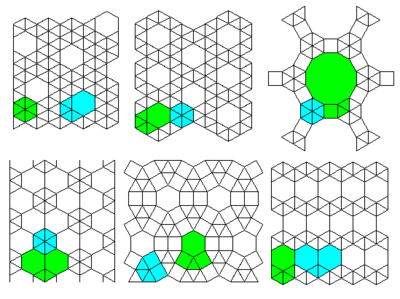


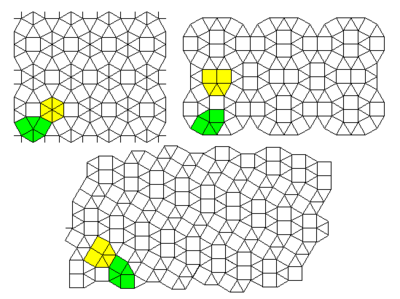















 (는) 임계 디스크 반경이다.
(는) 임계 디스크 반경이다. 











 객체 수와 같다.
객체 수와 같다.  임계 void fraction이다.
임계 void fraction이다. 

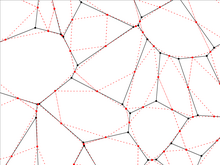



![{\displaystyle \eta _{c}=(\pi ^{d/2}/\Gamma [d/2+1])r^{d}N/L^{d}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90173c0ef117e66cd6feaf99b7e0f615aa0d83b7)




















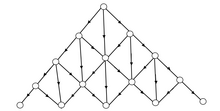













![{\displaystyle 1-3z+z^{3}-(1-z^{2})[3x^{2}y(1+y-y^{2})(1+z)+x^{3}y^{2}(3-2y)(1+2z)]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bca37fb3504d909546e2e4e7311696782d08b37c)









