팔각 프리즘

균일 팔각 프리즘
유형	프리즘 균일 다면체
요소들	F = 10, E = 24, V = 16(수평 = 2)
옆얼굴	8{4}+2{8}
슐레플리 기호	t{2,8} 또는 {8}×{}
와이토프 기호	2 8 2 2 2 4
콕시터 도표
대칭	D8h, [8,2], (*822), 주문 32
회전군	D8, [8,2],+ (822), 주문 16
참조	U76(f)
이중	팔각 디피라미드
특성.	볼록한 조노헤드론
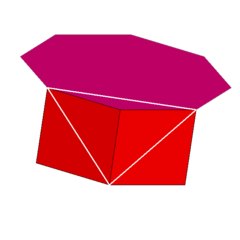정점수 4.4.8

기하학에서 팔각 프리즘은 네모난 면과 두 개의 정규 팔각모자로 이루어진 무한 프리즘 집합에서 여섯 번째다.

얼굴이 모두 규칙적이면 반정형 다면체다.

대칭

이름	디테트라곤 프리즘	디테트란각형 사다리꼴주의
이미지
대칭	D4h, [2,4], (*422)	D4d, [2+,8], (2*4)
건설	tr{4,2} 또는 t{4}×{},	s2{2,8},

이미지들

팔각형 프리즘은 구체의 타일링으로도 볼 수 있다.

사용하다

광학에서는 팔각 프리즘을 사용하여 영화 프로젝터에서 깜박임이 없는 이미지를 생성한다.

균일한 허니컴과 4폴리탑으로 된

이것은 세 개의 균일한 꿀벌의 원소다.

잘린 사각 프리즘 벌집	옴니트런 큐빅 벌집	런시타르드 큐빅 벌집

또한 다음과 같은 두 개의 4차원 균일 4폴리탑의 요소다.

런티런탈테서락트	옴니트룬탈테서락트

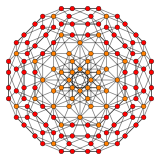관련 다면체

균일-곤 프리즘 계열

• v
• t

프리즘 이름	디조날 프리즘	(트리거) 삼각 프리즘	(Tetrangle) 사각 프리즘	오각형 프리즘	육각 프리즘	헵타곤 프리즘	팔각 프리즘	엔네오각 프리즘	십각형 프리즘	헨드각 프리즘	도십각 프리즘	...	아페이로곤 프리즘
다면체 이미지												...
구형 타일링 영상												평면 타일링 영상
정점 구성.	2.4.4	3.4.4	4.4.4	5.4.4	6.4.4	7.4.4	8.4.4	9.4.4	10.4.4	11.4.4	12.4.4	...	∞.4.4
콕시터 다이어그램												...

*n42 전분해 틸팅의 대칭 돌연변이: 4.8.2n v t
대칭 *n42 [n,4]	구면		유클리드 주	콤팩트 쌍곡선				파라콤.
	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
옴니트런어드 형상을 나타내다	4.8.4	4.8.6	4.8.8	4.8.10	4.8.12	4.8.14	4.8.16	4.8.∞
옴니트런어드 듀얼스	V4.8.4	V4.8.6	V4.8.8	V4.8.10	V4.8.12	V4.8.14	V4.8.16	V4.8.1987

외부 링크

• Weisstein, Eric W. "Octagonal prism". MathWorld.
• 팔각 프리즘의 인터랙티브