일체형

함수의 확실한 적분은 그 그래프로 둘러싸인 영역의 부호 있는 영역으로 나타낼 수 있다.

수학에서 적분은 변위, 면적, 부피 및 무한소 데이터를 결합하여 발생하는 다른 개념을 설명하는 방식으로 함수에 숫자를 할당합니다.적분을 찾는 과정을 적분이라고 합니다.미적분과 함께,^[a] 적분은 미적분의 기본적이고 필수적인 연산이며, 특히 임의의 형상의 영역, 곡선의 길이, 그리고 고체의 부피를 포함한 수학과 물리학의 문제를 해결하는 도구 역할을 한다.

여기에 열거된 적분은 유한 적분이라고 불리는 적분이며, 이는 실제 선의 두 점 사이의 주어진 함수의 그래프에 의해 경계되는 평면에서 영역의 부호 있는 영역으로 해석될 수 있다.일반적으로 평면 수평축 위의 영역은 양의 영역이고 아래 영역은 음의 영역입니다.적분은 또한 주어진 함수가 도함수인 역도함수의 개념을 참조한다.이 경우 이들을 무기한 적분이라고 합니다.미적분의 기본정리는 미분과 명확한 적분을 관련짓고 함수의 반미분이 알려졌을 때 함수의 확실한 적분을 계산하는 방법을 제공한다.

고대 그리스 수학에서 나온 면적과 부피를 계산하는 방법에도 불구하고, 적분 원리는 17세기 후반 아이작 뉴턴과 고트프리드 빌헬름 라이프니츠에 의해 독립적으로 공식화되었는데, 그는 곡선 아래의 영역을 극소 폭의 직사각형의 무한합으로 생각했다.베른하르트 리만은 나중에 적분의 엄밀한 정의를 내렸는데, 이는 지역을 무한히 얇은 수직 슬래브로 분할함으로써 곡선 영역의 면적을 근사하는 제한 절차에 기초한다.20세기 초, 앙리 르베그(Henri Lebegue)는 현재 르베그 적분이라고 불리는 것을 도입함으로써 리만의 공식을 일반화했다. 더 넓은 종류의 함수는 르베그 적분이라는 점에서 리만보다 더 강력하다.

통합은 기능의 유형 및 통합을 수행하는 도메인에 따라 일반화될 수 있습니다.예를 들어 둘 이상의 변수의 함수에 대해 선 적분을 정의하고 적분 간격을 해당 간격의 두 끝점을 연결하는 곡선으로 치환한다.면적분에서는 곡선이 3차원 공간에서의 면 조각으로 치환된다.

역사

계산 전 통합

적분을 결정할 수 있는 최초의 문서화된 체계적 기법은 고대 그리스 천문학자 에우독소스(기원전 370년경)의 소진 방법인데, 그는 영역이나 부피가 ^[1]알려진 무한한 수의 분할로 영역과 부피를 찾으려고 했다.이 방법은 기원전 3세기에 아르키메데스에 의해 더욱 개발되고 적용되었으며 원의 면적, 구의 표면적과 부피, 타원 면적, 포물선 아래의 면적, 회전 포물선 부분의 부피, 회전의 쌍곡선 부분의 부피, 그리고 나선형의 면적을 계산하는 데 사용되었다.l.^[2]

비슷한 방법은 서기 3세기경 류후이(劉,)에 의해 중국에서 독자적으로 개발되었으며, 그는 원의 면적을 찾기 위해 그것을 사용했다.이 방법은 이후 5세기에 중국의 부자 수학자 주충지와 주겅이 ^[3]구의 부피를 구하기 위해 사용하였다.

중동에서, 알하젠으로 라틴어로 표기된 하산 이븐 알-하이탐 (965년경–1040년경)은 네 번째 ^[4]힘의 합에 대한 공식을 도출했습니다.그는 그 결과를 이 함수의 적분이라고 불리는 것을 수행하기 위해 사용했는데, 여기서 적분 제곱과 4제곱의 합에 대한 공식은 ^[5]포물체의 부피를 계산할 수 있게 해주었다.

적분학의 다음 중요한 발전은 17세기까지 나타나지 않았다.이 시기에, 카발리에리의 불가시사블의 방법과 페르마의 연구는 카발리에리의 직교 ^[7]공식에서 $x$ 의ⁿ 적분을 최대 $n$ = $9$ 까지 계산하면서 현대 ^[6]미적분의 기초를 쌓기 시작했다.17세기 초에 Barrow와 Torricelli가 통합과 분화 사이의 연관성에 대한 첫 번째 힌트를 제공했다.바로우는 ^[8]미적분학의 기본정리에 대한 첫 번째 증거를 제공했다.Wallis는 Cavalieri의 방법을 일반화하여 x의 $적분$ 을 음의 힘 ^[9]및 분수력을 포함한 일반 거듭제곱으로 계산했습니다.

라이프니츠와 뉴턴

통합의 주요한 발전은 라이프니츠와 ^[10]뉴턴에 의해 미적분의 기본 정리가 독립적으로 발견되면서 17세기에 이루어졌다.그 정리는 적분과 미분 사이의 관계를 보여준다.이 접속과 비교적 쉽게 구별할 수 있는 접속을 조합하여 적분을 계산할 수 있습니다.특히, 미적분의 기본 정리는 훨씬 더 광범위한 종류의 문제를 풀 수 있게 해준다.라이프니츠와 뉴턴이 개발한 포괄적인 수학 체계도 중요성에 있어서 같다.무한소 미적분이라는 이름에서 연속 영역 내의 함수를 정밀하게 분석할 수 있었다.이 틀은 결국 현대 미적분이 되었고, 적분의 표기법은 라이프니츠의 작품에서 직접 도출되었다.

형식화

뉴턴과 라이프니츠는 통합에 대한 체계적인 접근을 제공했지만, 그들의 작업은 엄격함이 부족했다.버클리 주교는 뉴턴이 사용한 사라져가는 증분을 "떠난 양의 유령"^[11]이라고 부르며 기억할 수 있게 공격했다.미적분은 한계가 발달함에 따라 더욱 견고한 기반을 얻었다.통합은 처음에 리만에 ^[12]의해 한계를 사용하여 엄격하게 공식화되었습니다.비록 모든 유계 부분 연속 함수가 유계 구간에서 리만 적분 가능하지만, 그 후에 특히 푸리에 분석의 맥락에서 리만의 정의가 적용되지 않는 더 일반적인 함수가 고려되었고, 르베게는 측정에서 기초하는 적분의 다른 정의를 공식화했다. 분석).적분의 다른 정의, 리만과 르베그 접근법을 확장한 것이 제안되었다.실수계에 기초한 이러한 접근법은 오늘날 가장 일반적인 접근법이지만, 초실수계에 기초한 무한 리만 합계의 표준 부분으로서의 적분의 정의와 같은 대체 접근법이 존재한다.

과거 표기법

부정 적분의 표기법은 1675년 ^[13]고트프리드 빌헬름 라이프니츠에 의해 도입되었다.그는 문자 ( (긴 s)에서 ,을 suma ( umma, 라틴어로 "sum" 또는 "total"을 나타냄)의 약자로 변형했다.적분부호의 위와 아래에 한계가 있는 현대적 표기법은 1819~20년 경 프랑스 아카데미의 메무아르에서 조제프 푸리에에 의해 처음 사용되었고, ^[14]1822년 그의 책에 재인쇄되었다.

아이작 뉴턴은 적분을 나타내기 위해 변수 위에 작은 수직 막대를 사용하거나 변수를 상자 안에 넣었습니다.세로 막대는 구별을 나타내기 위해 $사용$ 되는 . $x$ 또는 x와혼동되기 쉬우며, 상자 표기법은 프린터가 재현하기 어려웠기 때문에 널리 ^[15]채택되지 않았습니다.

용어의 최초 사용

이 용어는 1690년 야콥 베르누이에 의해 라틴어로 처음 인쇄되었다: "Ergo et horum Integralia a equantur."^[16]

용어 및 표기법

일반적으로 구간 [ $a,$ $b]$ 에서 실수 $변수$ x에 대한 실수 값 $함수$ f $(x)$ 의 적분은 다음과 같이 기술된다.

\int _{a}^{b}f(x) , parames

적분 기호repres는 적분을 나타냅니다. $변수$ x의 미분이라고 하는 $기호$ dx는 적분 변수가 $x임$ 을 나타냅니다. $함수$ f $(x)$ 를 적분이라고 하고, $점$ $a$ 와 b를 적분 한계(또는 한계)라고 하며, 적분은 ^[17]적분 간격이라고 하는 구간 $[a,$ $b]$ 을 초과한다고 합니다.함수는 그 도메인에 대한 적분이 유한할 경우 적분할 수 있다고 한다.한계를 지정하면 적분은 확정 적분이라고 합니다.

다음과 같이 제한이 생략된 경우

{\displaystyle\int f(x),filename,}

적분은 무한 적분이라고 불리며, 이는 미분이 적분인 ^[18]함수의 클래스(반파생)를 나타낸다.미적분의 기본정리는 유한적분의 평가를 무한적분과 관련짓는다.무한 도메인 및/또는 다차원에서의 통합을 포함하기 위해 통합 표기법에는 몇 가지 확장 기능이 있습니다(이 문서의 뒷부분 참조).

고급 설정에서는 단순한 리만 적분만 사용하거나 정확한 적분 유형이 중요하지 않은 경우 dx를 $생략$ 하는 것이 일반적입니다.예를 들어 ${\textstyle \int _{a}^{b}(c_{1}f+c_{2}g)=c_{1}\int _{a}^{b}f+c_{2}\int _{a}^{b}g}$ ${\textstyle \int _{a}^{b}(c_{1}f+c_{2}g)=c_{1}\int _{a}^{b}f+c_{2}\int _{a}^{b}g}$ ${\textstyle \int _{a}^{b}(c_{1}f+c_{2}g)=c_{1}\int _{a}^{b}f+c_{2}\int _{a}^{b}g}$ ( ${\textstyle \int _{a}^{b}(c_{1}f+c_{2}g)=c_{1}\int _{a}^{b}f+c_{2}\int _{a}^{b}g}$ ${\textstyle \int _{a}^{b}(c_{1}f+c_{2}g)=c_{1}\int _{a}^{b}f+c_{2}\int _{a}^{b}g}$ ${\textstyle \int _{a}^{b}(c_{1}f+c_{2}g)=c_{1}\int _{a}^{b}f+c_{2}\int _{a}^{b}g}$ + ${\textstyle \int _{a}^{b}(c_{1}f+c_{2}g)=c_{1}\int _{a}^{b}f+c_{2}\int _{a}^{b}g}$ ${\textstyle \int _{a}^{b}(c_{1}f+c_{2}g)=c_{1}\int _{a}^{b}f+c_{2}\int _{a}^{b}g}$ g ) ${\textstyle \int _{a}^{b}(c_{1}f+c_{2}g)=c_{1}\int _{a}^{b}f+c_{2}\int _{a}^{b}g}$ c 1 ${\textstyle \int _{a}^{b}(c_{1}f+c_{2}g)=c_{1}\int _{a}^{b}f+c_{2}\int _{a}^{b}g}$ ${\textstyle \int _{a}^{b}(c_{1}f+c_{2}g)=c_{1}\int _{a}^{b}f+c_{2}\int _{a}^{b}g}$ f + ${\textstyle \int _{a}^{b}(c_{1}f+c_{2}g)=c_{1}\int _{a}^{b}f+c_{2}\int _{a}^{b}g}$ ${\textstyle \int _{a}^{b}(c_{1}f+c_{2}g)=c_{1}\int _{a}^{b}f+c_{2}\int _{a}^{b}g}$ ${\textstyle \int _{a}^{b}(c_{1}f+c_{2}g)=c_{1}\int _{a}^{b}f+c_{2}\int _{a}^{b}g}$ ${\textstyle \int _{a}^{b}(c_{1}f+c_{2}g)=c_{1}\int _{a}^{b}f+c_{2}\int _{a}^{b}g}$ ${\textstyle \int _{a}^{b}(c_{1}f+c_{2}g)=c_{1}\int _{a}^{b}f+c_{2}\int _{a}^{b}g}$ { $textstyle \int$ _ { $a$ }^{ $b$ （ c _ { $a }$ f + $c _$ { } g $=$ c _ { 1 $int$ _ { $a$ } f + $c$ _ 2 $int$ } $express$ { $b }$ 라고 ${\textstyle \int _{a}^{b}(c_{1}f+c_{2}g)=c_{1}\int _{a}^{b}f+c_{2}\int _{a}^{b}g}$ 쓸 수 있습니다.

해석

노란색 오른쪽 엔드포인트 파티션 5개와 녹색 왼쪽 엔드포인트 파티션 12개로 0 ~

1

의

x의 적분에 대한 근사치

적분은 많은 실제 상황에서 나타납니다.예를 들어 바닥이 평평한 직사각형인 수영장의 길이, 폭, 깊이에서 수영장이 담을 수 있는 물의 부피, 수면 면적, 가장자리 길이를 파악할 수 있다.그러나 바닥이 둥근 타원형인 경우 적분은 이러한 양에 대한 정확하고 엄격한 값을 찾아야 합니다.어느 경우든 원하는 양을 무한히 많은 극소 조각으로 나눈 후 정확한 근사치를 얻기 위해 조각을 합해도 된다.

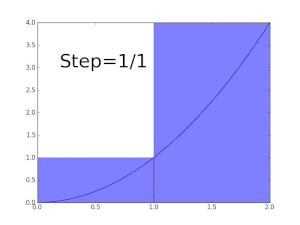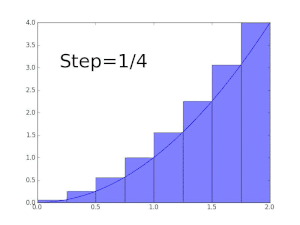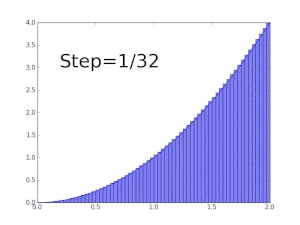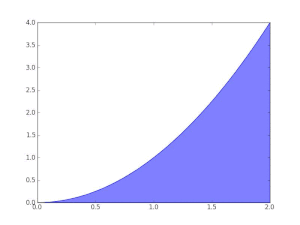
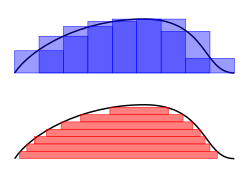
예를 들어 x = $0$ 과 x = $1$ $사이$ 의 $함수$ f $(x) = δx$ 의 그래프로 둘러싸인 영역의 면적을 구하려면 $5단계(0, 1/$ 5 $,$ $2$ /5, $..., 1$ )로 간격을 교차시킨 다음 각 조각의 오른쪽 끝 높이( $θ0, θ1/5, θ2 / 5),$ ..., 합계를 사용하여 직사각형을 채우면 된다 $.$

\displaystyle \textstyle \frac {1}{5}\leftfrac {5}+{\frac {2}{5}}\leftfrac {2}{5}-{\frac {1}{5}-{\frac {5}+{\frac {5}}+{\frac {\frac}}{\frac {\frac}}}}{\frac {\frac}}}}}{\frac {\fright}}}}{\cdotslight}}}}}}}}}

정확한 값보다 큰 값입니다.또는 이러한 서브 인터벌을 각 피스의 왼쪽 끝 높이로 치환하면 근사치가 너무 낮아집니다.이러한 서브 인터벌을 12개 사용하면 근사 면적이 0.6203에 불과합니다.그러나 조각 수가 무한대로 증가하면 원하는 면적의 정확한 값(이 경우 $2/$ 3)에 도달합니다.쓰다

{\displaystyle \int _{0}^1}{\displayrt {x}},syslog=syslogfrac {2}{3}},

$즉,$ 함수 $값$ 의 $가중치$ 합[0, 1 $]$ 에 dx로 $표시$ 된 극소 단계 폭을 곱한 결과이다.

다르부스 섬

Darboux

함수

의

상한합 2

y = x

Darboux

함수

의 하위

합계 2

y = x

정식 정의

리만 합집합

적분을 공식적으로 정의하는 방법은 여러 가지가 있지만, 모두 동일한 것은 아닙니다.이러한 차이는 주로 다른 정의에서는 통합이 불가능할 수 있는 다른 특수한 경우를 다루기 위해 존재하지만 때로는 교육학적 이유로도 존재한다.가장 일반적으로 사용되는 정의는 리만 적분 및 르베그 적분입니다.

리만 적분

리만 적분은 ^[20]간격의 태그된 분할에 대한 함수의 합계로 정의됩니다.실선상의 닫힌 간격 [ $a,$ $b]$ 의 태그가 달린 파티션은 유한 시퀀스이다.

\displaystyle a=x_{0}\leq t_{1}\leq t_{2}\leq \cdots \leq x_{n-1}\leq t_{n}=b,\!}.

이것은 구간 [ $a,$ $b]$ 를 i에 $의해$ 색인화된 n개의 하위 구간 [ $x i -1, x i$ ]로 분할하고, 각각의 구간은 $구분점 i$ t [ [ $x i -1, x i$ ]로 "태그 부착"된다.이러한 태그가 달린 분할에 대한 $함수$ f의 리만 합은 다음과 같이 정의된다.

\displaystyle \sum _{i=1}^{n}f(t_{i}),\Delta _{i};}

따라서, 합계의 각 항은 주어진 하위 구간의 구별점에서 함수 값과 동일한 높이와 하위 구간의 폭인 $δ i$ = $x-x$ 를_i_i−1 갖는 직사각형의 면적이다.이러한 태그가 달린 파티션의 메쉬가 파티션에 의해 형성되는 가장 큰 $서브인터벌$ 의_i=1...n 폭인 $max i$ δ입니다.구간 [ $a,$ b]에 걸친 $함수$ f의 리만 적분은 다음과 같은 ^[21]경우 S와 $같다$ .

\varepsilon >0

(\displaystyle \varepsilon

>

0)

에

\varepsilon >0

대해 0

(\

displaystyle \

delta

>

0)

이

\delta >0

존재합니다.이러한 경우

,

메쉬가 "\

displaystyle

\delta

\delta

보다 작은 태그가 달린 파티션

[a,b]

[

a

, b

[a,b]

](a

, b

)에

[a,b]

대해서는,

\displaystyle \left S-\sum _{i=1}^{n}f(t_{i}),\Delta _{i}\right <\varepsilon .}

선택한 태그가 각 구간의 최대값(각각 최소값)을 제공하는 경우, 리만 합계가 상위(각각 하위) 다르부 합계가 되어 리만 적분과 다르부 적분 간의 밀접한 관계를 나타냅니다.

르베그 적분

Comparison of Riemann and Lebesgue integrals

리만-다르부 적분(위)과 르베그 적분(아래)

이론과 응용 모두에서 적분 하의 한계로 넘어갈 수 있는 것이 종종 흥미롭다.예를 들어, 적절한 의미에서 문제에 대한 해결책에 가까운 일련의 함수를 구성할 수 있습니다.그러면 솔루션 함수의 적분은 근사치의 적분의 한계여야 합니다.그러나, 한계로 얻을 수 있는 많은 함수는 리만 적분이 아니기 때문에, 그러한 한계 정리는 리만 적분에는 적용되지 않는다.따라서, 더 넓은 클래스의 함수를 ^[22]통합할 수 있는 적분의 정의를 갖는 것이 매우 중요합니다.

이러한 적분은 르베그 적분으로서, 적분 가능한 함수의 클래스를 확대하기 위해 다음과 같은 사실을 이용한다: 함수의 값이 도메인 전체에 재배치되면, 함수의 적분은 동일하게 유지되어야 합니다.그래서 앙리 르베그(Henri Lebegue)는 폴 몽텔(Paul Montel)^[23]에게 보낸 편지에서 이 적분을 설명하면서 자신의 이름이 새겨진 적분을 소개하였다.

호주머니에 모아둔 돈을 갚아야 한다나는 지폐와 동전을 주머니에서 꺼내서 총액이 될 때까지 순서대로 채권자에게 준다.이것은 리만 적분이다.하지만 나는 다르게 진행할 수 있다.주머니에서 돈을 다 꺼낸 후 동일한 금액으로 지폐와 동전을 주문하고 몇 무더기를 채권자에게 차례로 지불합니다.이건 내 적분이야

Folland가 말한 것처럼, " $f$ 의 리만 적분을 계산하기 위해 $,$ $하나$ 는 $도메인$ 을 부분간격으로 분할한다 $."$ 반면, 르베그 적분에서는 "1은 사실상 ^[24]f의 $범위$ 를 분할하고 있다."따라서 르베그 적분의 정의는 측정값 μ로 시작됩니다.가장 간단한 경우, 레베그 $측정값$ μ( $A)$ 는 $구간$ A = [ $a,$ $b]$ 의 $폭$ b - $a$ 이므로, 르베그 적분은 둘 다 존재할 ^[25]때 (적절한) 리만 적분과 일치한다.보다 복잡한 경우 측정되는 세트는 연속성이 없고 간격과 유사하지 않고 고도로 단편화될 수 있습니다.

"f " 철학의 $범위$ 확대"를 사용하여, 음이 아닌 $함수 f$ : R → $R$ 의 적분은 y = $t$ 와 y $= t$ + $dt$ $사이$ 의 얇은 수평 스트립 사이의 면적의 $합$ 이 되어야 한다.이 면적은 $단지$ μ{ $x$ : $f (x)$ > t} $dt$ 입니다.f $(t) = μ$ { $x$ : $f (x)$ > $t$ $}$ 로 $하자 *$ .다음으로 $f$ 의 르베그 적분은 다음과 같이 정의된다.

\int f=\int _{0}^{\infty}f^{*}(t),dt

여기서 오른쪽의 적분은 일반적인 부적절한 리만 적분이다( $f$ 는^∗ 엄밀하게 감소하는 양의 함수이므로 잘 정의된 부적절한 리만 ^[26]적분이 있음).적절한 함수 클래스(측정 가능한 함수)에 대해 르베그 적분을 정의합니다.

f $그래프$ 와 x축 사이의 영역 영역의 절대값 합계가 ^[27]유한할 경우 일반적인 $측정가능함수$ f는 르베그 적분가능하다.

\displaystyle \int _{E} f , d \ mu < + \ infty }

이 경우 적분은 리만의 경우와 마찬가지로 x축 위 영역과 x축 ^[28]아래 영역의 차이입니다.

\displaystyle \int _{E}f,d\mu =\int _{E}f^{+},d\mu -\int _{E}f^{-},d\mu }

어디에

{\displaystyle{alignedat}{3}&f^{+}(x)&&{}={}\max\{f(x),0\}&{}={\cases}f(x),&{\text{if}}f(x)>0,\text{f},\end{cases},\f^{-}(x)&{max\{f},{f}&{x},{\cases},}}\end{case}\end{alignedat}}

기타 통합

리만 적분과 르베그 적분은 가장 널리 사용되는 적분 정의이지만, 다음을 포함한 많은 다른 정의들이 존재한다.

Darboux 적분은 Darbous sums(제한된 Riemann sums)에 의해 정의되지만, 함수는 Darboux 적분과 동등합니다. Darboux 적분은 리만 적분이 가능한 경우에만 Darbous 적분입니다.Darboux 적분은 리만 적분보다 정의하기 쉽다는 장점이 있습니다.
변수가 아닌 함수에 대해 적분하는 리만 적분의 확장인 리만-스틸테제스 적분.
요한 라돈에 의해 더욱 개발된 르베그-스틸트제 적분은 리만-스틸트제 적분과 르베그 적분을 모두 일반화한다.
측정에 의존하지 않고 르베그 적분 및 르베그-스틸테즈 적분을 포함하는 다니엘 적분.
Alfréd Haar가 1933년에 도입한 국소 콤팩트 위상군의 통합에 사용되는 Haar 적분.
Arnaud Denjoy, Oskar Perron 및 Jaroslav Kurzweil에 의해 다양하게 정의되고 Ralph Henstock에 의해 개발된 Henstock-Kurzweil 적분.
이토 적분 및 스트라토노비치 적분. 브라운 운동과 같은 반마틴갈레와 관련하여 적분을 정의한다.
영 적분, 이것은 무한 변동의 특정 함수와 관련된 리만-스틸테스의 일종이다.
조경로 적분은 일부 추가 "조경로" 구조를 갖춘 함수에 대해 정의되며 반직렬 및 부분 브라운 운동과 같은 프로세스에 대한 확률적 통합을 일반화한다.
1953년 프랑스 수학자 구스타브 초케가 만든 준가법적 또는 초가법적분인 초케 적분.

특성.

선형성

닫힌 간격 [ $a,$ $b]$ 에 있는 리만 적분 가능 함수의 집합은 스칼라에 의한 점별 덧셈과 곱셈 연산, 그리고 적분의 연산 아래 벡터 공간을 형성한다.

f\mapsto \int _{a}^{b}f(x)\;displaystyle

이 벡터 공간에서의 선형 함수입니다.따라서, 적분 가능한 함수의 집합은 선형 결합을 취하면 닫히고, 선형 결합의 적분은 ^[29]적분의 선형 결합이다.

\displaystyle \int _{a}^{b}(\alpha f+\int g)(x),\alpha \int _{a}^{b}f(x),\int \int _{a}^{b}g(x),\int.}

마찬가지로, $측정$ μ를 갖는 주어진 측정 $공간$ E 상의 실수치 르베그 적분함수 집합은 선형 결합을 취하여 닫히고, 따라서 벡터 공간을 형성하며, 르베그 적분

\displaystyle f\mapsto \int _{E}f,d\mu }

는 이 벡터 공간상의 선형 함수이므로 다음과 같습니다.^[28]

\displaystyle \int _{E}(\alpha f+\mu g),d\mu =\alpha \int _{E}f,d\mu +\display \int _{E}g,d\mu .}

보다 일반적으로 국소적으로 콤팩트한 $위상장$ K, $f$ : E → $V$ 위의 국소적으로 콤팩트한 완전 위상 벡터 $공간$ V의 값을 취하여 측정 공간 $(E,$ μ) 상의 모든 측정 가능 함수의 벡터 공간을 고려한다.그런 다음 V $요소$ 또는 기호 $,$ 를 각 기능에 $할당$ 하는 추상 적분 맵을 정의할 수 있다.

\displaystyle f\mapsto \int _{E}f,d\mu ,,}

선형 ^[30]조합과 호환됩니다.이 상황에서 선형성은 적분이 V의 $요소$ (즉, "무한")인 함수의 부분 공간에 대해 유지됩니다.가장 중요한 특수한 $경우$ 는 K가 $R$ , C 또는 p-adic 숫자의 $필드 p$ Q의 유한 확장이고, $V$ 가 K $위$ 의 유한 차원 벡터 공간이고, K = $C$ 와 V가 복소 힐베르트 공간일 때 $발생$ 한다.

선형성은 일부 자연 연속성 특성 및 "단순" 함수의 특정 클래스에 대한 정규화와 함께 적분의 대체 정의를 제공하기 위해 사용될 수 있다. $이것$ 은 집합 X의 실수값 함수의 경우에 대한 다니엘의 접근법이며, 니콜라 부르바키에 의해 국소적으로 콤팩트한 위상 벡터 공간에서 값을 갖는 함수로 일반화되었다.적분의 자명한 특성은 Hildebrandt 1953을 참조하십시오.

불평등

다수의 일반 부등식은 닫힌 경계구간 [ $a,$ $b]$ 에서 정의된 리만 적분 가능 함수에 대해 유지되며 적분의 다른 개념(르베그 및 다니엘)으로 일반화될 수 있다.

상한과 하한.[ $a,$ $b]$ 위의 적분 가능 $함수$ f는 반드시 그 구간에서 유계된다.따라서 [ $a,$ $b]의$ $모든$ x에 대해 m $f$ f ( $x) for$ M이 $되도록$ 실수 $m$ 과 M이 존재한다.따라서 [ $a,$ $b]$ 위의 f의 $하한$ 및 상한 합계가 각각 m $(b$ $- a$ ) $및$ M $(b$ - $a)$ 에 의해 제한되므로 다음과 같이 된다. $m(b-a)\leq \int _{a}^{b}f(x),dx\leq M(b-a)입니다.$
함수 ^[31]간의 불평등.[ $a,$ $b]의$ $각$ x에 대해 f $(x) g$ g $(x)$ 일 경우 $f$ 의 상한합과 하한합은 각각 $g$ 의 상한합과 하한합에 의해 위쪽으로 경계된다.따라서 $\int _{a}^{b}f(x), scap\leq \int _{a}^{b}g(x), scap$ M $(b$ - $a)$ 은 [ $a,$ $b]$ 보다 $값$ 이 M인 상수 함수의 적분이기 $때문$ 에 위의 부등식을 일반화한다.또한 함수 간의 불평등이 엄격하면 적분 간의 불평등도 엄격합니다.즉, [ $a,$ $b]의$ $각$ x에 대해 f $(x)$ < $g (x)$ 일 $경우$ , $(\displaystyle \int _{a}^{b(x), scap <\int _{a}^{b}g(x), scap)}$
서브 인터벌[ $c,$ $d]$ 가 [ $a,$ $b]$ 의 하위 $구간$ 이고 f $(x)$ 가 $모든$ x에 대해 음이 아닌 경우 $,$ $\int _{c}^{d}f(x) , sc\leq \int _{a}^{b}f(x) , scap$
함수의 제품과 절대값. $f$ 와 g가 2개의 함수인 $경우$ , 점별 곱과 검정력 및 절대값을 고려할 수 있습니다. $\displaystyle (fg)(x)=f(x)g(x),\;f^{2}(x)=(f(x))^{2},\; f(x)= f(x) .}$ f가 [ $a,$ $b]$ 에서 리만 적분 가능한 $경우$ f에 $대해서도$ 마찬가지입니다. ${\displaystyle \left \int _{a}^{b}f(x) , right \leq \int _{a}^{b} f(x) , response 。$ $또한$ $f$ 와 g가 둘 다 리만 적분가능하다면 $fg$ 도 리만 적분가능하다. $\displaystyle \left(\int _{a}^{b)(x)(fg)(x),\right)^{leq \left(\int _{a}^{b(x)^2},f(x)\left(\int _{a}^{b}g(x)g(x)\right).}$ 코시-슈바르츠 부등식으로 알려진 이 부등식은 힐베르트 공간 이론에서 중요한 역할을 한다. 힐베르트 공간 이론에서는 왼쪽이 $구간$ 에서 두 제곱 적분 함수 $f$ 와g의 내적물로 해석된다 $.$
핼더 ^[32]부등식.는 피와 q두 실수를, 1≤ p,.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac .num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-과≤ ∞ q 있다고 가정하자Parser-output.sfrac .den{border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}1/p+1/q=1, f, g두Riemann-integrable 기능. $그러면$ 함수 $f$ 와 g도 적분할 수 있고 다음과 같은 쾰더의 부등식이 유지된다. $(\displaystyle \left \int f(x)g(x), right \left(\int \left f(x)\right ^{p}, right ^{p}\left(\int \left g(x)\right ^{q}, right)^1/q}).}$ p = $q$ = $2일$ 때, 쾰더의 부등식은 코시-슈바르츠 부등식이 된다.
민코프스키 부등식.^[32]p ≤ $1$ 이 $실수$ 이고 $f$ 와 g가 리만 적분 함수라고 $가정$ 합니다. $f, p g p$ , $f$ + $g$ 도^p 리만 적분 가능하며 다음과 같은 민코프스키 부등식이 성립한다. $\displaystyle \left(\int \left f(x)+g(x)\right ^{p}(\int \left f(x)\right ^{p}\left(\int \left f(x)\right)^{p}+\left(\int \left g(x)\right ^{p},\right)^1/p}.}$ L 공간의 구성에는^p 르베그 적분에 대한 이 부등식의 유사체가 사용된다.

관습

이 절에서 $f$ 는 실수값 리만 적분함수이다.적분

\int _{a}^{b}f(x),param

$[a, b$ ] 간격에 걸쳐 정의됩니다(a, b는 < $b$ 의 $경우$ 입니다. $즉$ , 함수 f의 상한 및 하한 합계가 값 $x$ 가_i 증가하는 파티션 $a$ = $x 0 x 1$ x . . . $\leq$ $x n$ = $b$ 에서 평가된다는 것을 의미합니다.기하학적으로, 이는 통합이 "왼쪽에서 오른쪽으로" 이루어지며, 지수가 높은 구간이 지수가 낮은 구간 오른쪽에 있는 구간 [ $x i,$ $x i +1]$ 내에서 f를 $평가함$ 을 나타냅니다.간격의 끝점인 $값$ $a$ 와 b를 $f$ 의 적분 한계라고 부릅니다.통합은 a > ^[17] $b$ 의 $경우$ 에도 정의할 수 있습니다.

\int _{a}^{b}f(x), param=-\int _{b}^a}f(x), parames

$a$ = b의 $경우$ 이는 다음을 의미합니다.

\int _{a}^{a}f(x), syslog=0.

첫 번째 규칙은 [ $a,$ $b]$ 의 하위 간격에 대해 적분을 취하는 것을 고려하기 위해 필요하다. 두 번째 규칙은 퇴화 간격 또는 한 점에 대해 적분이 0이어야 한다고 말한다.첫 번째 규칙의 한 가지 이유는 구간 [ $a,$ $b]$ 에서의 $f$ 의 적분성은 f가 임의의 서브구간 $[c,$ $d]$ 에서 적분할 수 $있음$ 을 의미하지만, 특히 적분에는 c가 [ $a,$ $b]의$ 요소라면 $다음$ 과 같은 특성이 있기 때문이다.^[29]

\int _{a}^{b(x), param=\int _{a}^c}f(x), param+\int _{c}^{b(x), param.

첫 번째 규칙에서 결과적인 관계는

{\displaystyle {displaystyle}{c}{f(x), syslog&{}=\int _{a}{b}f(x), syslog\&{}=\int _{a}{b}f(x), syslog+\int _{c}{c}f(x)\int _{a}f(x}, syslog&{c}{c}{c}f}{c}f}f}{f}{f},

그런 다음 $a$ , b $및$ $c$ 의 모든 주기적 순열에 대해 잘 정의됩니다.

미적분의 기본 정리

미적분의 기본정리는 미분과 적분은 역연산이라는 진술이다: 연속함수가 먼저 적분되고 그리고 나서 미분된다면, 원래의 함수가 ^[33]검색된다.미적분의 두 번째 기본 정리라고도 불리는 중요한 결과는 ^[34]적분할 함수의 역도함수를 사용하여 적분을 계산할 수 있게 해준다.

제1정리

f를 닫힌구간에서 정의된 연속 실수값 $함수$ 라고 $가정$ 합니다 [a, $b].$ [ $a,$ $b]$ 의 $모든$ x에 대해 F를 다음과 같이 $정의$ 한다.

F(x)=\int _{a}^{x}f(t),dt

다음으로 $F$ 는 [ $a,$ $b]$ 에서 연속이며, $개방$ 간격 $(a,$ b)에서 미분 가능하다.

F'(x)=f(x)

모든 x $in$ $(a$ , $b$ )에 대해서.

제2정리

f를 [ $a,$ $b]$ 에서 $반파생$ F를 허용하는 닫힌 구간 [ $a,$ $b$ ]에서 정의된 실수값 함수라고 $하자$ . $즉$ , $f$ 와 F는 [ $a,$ $b]$ 의 $모든$ x에 대해 다음과 같은 함수이다.

f(x)=F'(x)

f가 [ $a,$ $b]$ 에 적분할 수 있는 $경우$

\displaystyle \int _{a}^{b}f(x),dx=F(b)-F(a)}

내선번호

부적절한 통합

잘못된 정수

\int _{0}^{\infty }{\frac {dx}{(x+1){\sqrt {x}}}}=\pi

0

\int _{0}^{\infty }{\frac {dx}{(x+1){\sqrt {x}}}}=\pi

∞

\int _{0}^{\infty }{\frac {dx}{(x+1){\sqrt {x}}}}=\pi

(

\int _{0}^{\infty }{\frac {dx}{(x+1){\sqrt {x}}}}=\pi

+ 1)

\int _{0}^{\infty }{\frac {dx}{(x+1){\sqrt {x}}}}=\pi

\int _{0}^{\infty }{\frac {dx}{(x+1){\sqrt {x}}}}=\pi

{\ { \

displaystyle

\

int _

{ 0 }^{ \

infty

}{ \

frac

{

（

x + 1) { \

frac

rt {

\int _{0}^{\infty }{\frac {dx}{(x+1){\sqrt {x}}}}=\pi

x }} = \

pi

} 에는

\int _{0}^{\infty }{\frac {dx}{(x+1){\sqrt {x}}}}=\pi

도메인과 범위 양쪽의 간격이 무제한입니다.

"올바른" 리만 적분은 적분자가 적분 한계로 묶인 닫힌 경계 구간에서 정의되고 유한하다고 가정한다.이러한 조건 중 하나 이상이 충족되지 않으면 부적절한 적분이 발생합니다.어떤 경우에 그러한 적분은 순차적으로 더 큰 간격의 적절한 리만 적분 시퀀스의 한계를 고려함으로써 정의될 수 있다.

구간이 예를 들어 상한에 있는 경우 해당 엔드포인트가 무한대로 ^[35]이동함에 따라 부적절한 적분이 제한됩니다.

\displaystyle \int _{a}^{\infty }f(x), ph=\lim _{b\to\infty }\int _{a}^{b}f(x), ph(x)}

예를 들어 (a, b $)$ 와 $같이$ integrand가 하프 오픈 인터벌에서만 정의되거나 유한한 경우, 다시 한 번 제한은 유한한 ^[36]결과를 제공할 수 있습니다.

\int _{a}^{b(x)}, ph=\lim _{\varepsilon \to 0}\int _{a+\ilon }^{b(x),param

즉, 부적절한 적분은 적분 간격의 1개의 엔드포인트가 지정된 실수 또는 $"-"$ 중 하나에 접근하기 때문에 적절한 적분의 제한입니다.더 복잡한 경우에는 양쪽 끝점 또는 내부 점에 한계가 필요합니다.

다중 통합

이중 적분은

z=f(x,y)

z

z=f(x,y)

(

z=f(x,y)

,

z=f(x,y)

) {{

displaystyle

z

=f(x,y)}

아래의 볼륨을 계산합니다.

한 변수의 양의 함수의 정의 적분이 함수의 그래프와 x축 사이의 영역의 적분을 나타내듯이, 두 변수의 정의 함수의 이중 적분은 함수에 의해 정의된 표면과 ^[37]그 영역을 포함하는 평면 사이의 영역의 부피를 나타낸다.예를 들어, 2차원의 함수는 x와 y의 두 실변수에 의존하며, 두 $R=[a,b]\times [c,d]$ 의 데카르트 곱으로 주어진 직사각형 R 위의 함수 f의 적분은 R $R=[a,b]\times [c,d]$ [ $a$ , $R=[a,b]\times [c,d]$ × [ $R=[a,b]\times [c,d]$ c , d $]$ \ $displaystyle$ R $=$ [ a , $b$ ] \ $times$ [ c , d $R=[a,b]\times [c,d]$ ] } 로 $R=[a,b]\times [c,d]$ 쓸 수 있다.

\displaystyle \int _{R}f(x,y),dA}

여기서 차분 $dA$ 는 면적과 관련하여 통합이 이루어졌음을 나타냅니다.이 이중 적분은 리만 합계를 사용하여 정의할 수 있으며, 영역 ^[38]R 위의 z = $f (x, y)$ $그래프$ 에서 (서명된) 부피를 나타냅니다.적절한 조건(예: f가 연속인 경우)에서 푸비니의 정리는 이 적분이 등가 반복^[39] 적분으로 표현될 수 있다고 말한다.

\displaystyle \int _{a}^{b}\left[\int _{c}^{d}f(x,y),dy\right],parames}

이것에 의해, 1 차원 적분 계산의 이중 적분 계산의 문제가 경감됩니다.따라서 R 위의 적분에 대한 다른 표기법에서는 이중 ^[38]적분 부호가 사용됩니다.

\displaystyle _{R}f(x,y),dA}

보다 일반적인 도메인 간의 통합이 가능합니다. $\mathbb {R} ^{n}$ 의 n차원 영역 $D$ 에 걸친 부피와 $관련$ 된 함수 f의 적분은 $다음$ 과 같은 기호로 표시됩니다 $.$

\displaystyle \int _{D}f(\mathbf {x})d^{n}\mathbf {x} \ =\int _{D}f,dV.}

라인 인테그레이션 및 서페이스 인테그레이션

선 적분은 곡선을 따라 요소를 합산합니다.

적분 개념은 곡선 및 고차원 공간 내부의 표면과 같은 보다 일반적인 통합 영역으로 확장될 수 있습니다.이러한 적분은 각각 선적분 및 표면적분으로 알려져 있습니다.이것들은 벡터장을 다룰 때처럼 물리학에서 중요한 응용 분야를 가지고 있다.

선 적분(경로 적분이라고도 함)은 적분할 함수가 ^[40]곡선을 따라 평가되는 적분입니다.다양한 라인 인테그레이션이 사용되고 있습니다.닫힌 곡선의 경우 등고선 적분이라고도 합니다.

통합되는 함수는 스칼라 필드 또는 벡터 필드일 수 있습니다.선 적분 값은 곡선의 모든 지점에서 필드의 값의 합으로, 곡선의 일부 스칼라 함수(일반 호 길이 또는 벡터 필드의 경우 곡선의 ^[41]미분 벡터가 있는 벡터 필드의 스칼라 곱)에 의해 가중치가 부여됩니다.이 가중치는 간격에 정의된 단순한 적분과 선 적분을 구분합니다.물리학의 많은 간단한 공식은 선 적분 측면에서 자연 연속 아날로그를 가지고 있다. 예를 들어, 작업이 힘과 같다는 사실, $F$ 에 변위, $s$ 를 곱한 것은 (벡터 양으로) 다음과 ^[42]같이 표현될 수 있다.

W=\mathbf {F} \cdot \mathbf {s} .

전계나 중력장 등의 $벡터장$ F에서 $경로$ C를 따라 이동하는 물체에 대해 $s$ 에서 $s + ds$ 로 이동하는 미분작업을 가산하여 물체에 대해 이루어지는 총작업량을 구한다.그러면^[43] 라인에 적분이 됩니다.

W=\int _{C}\mathbf {F} \cdot d\mathbf {s} .

표면 적분의 정의는 표면을 작은 표면 요소로 분할하는 데 의존합니다.

표면 적분은 표면(공간에서 곡선 집합일 수 있음) 상의 적분에 대해 이중 적분을 일반화하며, 선 적분의 이중 적분 아날로그로 생각할 수 있다.통합되는 함수는 스칼라 필드 또는 벡터 필드일 수 있습니다.지표면 적분 값은 지표면의 모든 점에 있는 필드의 합입니다.이는 표면을 표면 요소로 분할하여 리만 ^[44]합계를 분할함으로써 달성할 수 있습니다.

표면 적분 적용의 예로서 $표면$ S의 $벡터장$ v를 고려한다. 즉, $S$ 의 $각$ 점 x에 대해 v $(x)$ 는 벡터이다.v(x $)$ 가 x에서 유체의 $속도$ 를 $결정$ 하도록 유체가 S를 통해 흐른다고 상상해 보십시오.플럭스는 단위 시간 $중$ S를 통과하는 유체의 양으로 정의됩니다.플럭스를 구하려면 단위 표면이 $S$ 에 수직인 $v$ 의 도트곱을 각 지점에서 구해야 합니다. 그러면 ^[45]표면에 통합된 스칼라 필드가 생성됩니다.

\displaystyle \int _{S}{\mathbf {v}\cdot \,d{\mathbf {S} }}

이 예에서 유체 플럭스는 물이나 공기와 같은 물리적 유체 또는 전기 또는 자속으로부터 발생할 수 있습니다.따라서 표면 적분은 물리학, 특히 고전적인 전자기 이론에서 응용된다.

등고선 적분

복소해석학에서 적분자는 실수 변수 $x$ 의 실함수 대신 복소 $변수$ z의 복소값 함수이다.복소함수가 복소평면에서 $(\displaystyle\gamma)$ 를 $\gamma$ 따라 적분되었을 때 적분은 다음과 같이 표시된다.

\displaystyle \int _{\display }f(z),dz}

이를 등고선 적분이라고 합니다.

미분 형식의 적분

미분 형식은 다변수 미적분, 미분 위상 및 텐서 분야에서 수학적 개념입니다.차동 양식은 차수별로 정리되어 있습니다.예를 들어, 단일 형식은 다음과 같은 좌표의 차분의 가중치 합입니다.

E(x,y,z),dx+F(x,y,z),dy+G(x,y,z),dz

여기서 E, F, G는 3차원의 함수이다.미분 일식은 지향 경로 상에 통합될 수 있으며, 결과 적분은 선 적분을 쓰는 또 다른 방법일 뿐이다.여기서 기본미분 dx, dy, dz는 3개의 좌표축에 평행한 극소방향 길이를 측정한다.

미분 2-폼은 형식의 합계입니다.

\displaystyle G(x,y,z),dx\wedge dy+E(x,y,z),dz\wedge dx.}

여기서 기본 2가지 $dx\wedge dy,dz\wedge dx,dy\wedge dz$ $dx\wedge dy,dz\wedge dx,dy\wedge dz$ x $dx\wedge dy,dz\wedge dx,dy\wedge dz$ $dx\wedge dy,dz\wedge dx,dy\wedge dz$ y $dx\wedge dy,dz\wedge dx,dy\wedge dz$ $dx\wedge dy,dz\wedge dx,dy\wedge dz$ $dx\wedge dy,dz\wedge dx,dy\wedge dz$ d $dx\wedge dy,dz\wedge dx,dy\wedge dz$ $dx\wedge dy,dz\wedge dx,dy\wedge dz$ y $dx\wedge dy,dz\wedge dx,dy\wedge dz$ d $dx\wedge dy,dz\wedge dx,dy\wedge dz$ { $style$ dx $\wedge$ dy, $dz\wedge$ dx, $dy\wedge dz}$ 는 $dx\wedge dy,dz\wedge dx,dy\wedge dz$ 좌표 2평면에 평행한 방향 영역을 측정합니다.기호 ${\(\displaystyle$ \ $wedge)$ 는 $\wedge$ 쐐기곱을 나타내며, 쐐기곱은 쐐기곱을 나타내며, 쐐기곱은 쐐기곱을 나타내며, 쐐기곱은 쐐기곱과 유사하다.배향된 표면에 2가지 형태를 적분할 수 있으며, 그 적분은 E $i$ + $E\mathbf {i} +F\mathbf {j} +G\mathbf {k}$ + $E\mathbf {i} +F\mathbf {j} +G\mathbf {k}$ $E\mathbf {i} +F\mathbf {j} +G\mathbf {k}$ k k k k k k k k k k k k k + $F$ \ $mathbf$ { $j }$ + $G$ \ mathbf { j } + G \ $mathbf$ { k $E\mathbf {i} +F\mathbf {j} +G\mathbf {k}$ 의 플럭스를 주는 표면 적분과 같다.

교차곱과 3차원 벡터 미적분과 달리, 쐐기곱과 미분 형식의 미적분은 임의의 차원 및 보다 일반적인 다양체(곡선, 표면 및 이들의 고차원 아날로그)에서 의미가 있습니다.외부 도함수는 벡터 미적분의 구배와 컬의 역할을 하며, 스톡스의 정리는 벡터 미적분의 세 가지 이론, 즉 발산 정리, 그린 정리, 켈빈-스토크스 정리를 동시에 일반화한다.

총계

적분의 이산적 등가물은 합계입니다.르베그 적분이나 시간 척도 미적분 이론을 사용하여 합계와 적분을 동일한 기초 위에 둘 수 있습니다.

기능 통합

변수(또는 물리학에서는 공간 또는 시간 차원)가 아닌 함수 공간에 걸쳐 수행되는 적분을 함수 적분이라고 합니다.

적용들

적분은 많은 영역에서 광범위하게 사용됩니다.예를 들어, 확률론에서 적분은 일부 랜덤 변수가 특정 ^[46]범위 내에 들어갈 확률을 결정하는 데 사용됩니다.또한, 전체 확률 밀도 함수의 적분은 1이어야 하며, 이는 음수 값이 없는 함수가 밀도 함수가 될 ^[47]수 있는지 여부를 검정합니다.

적분은 곡선 경계가 있는 2차원 영역의 면적 계산과 곡선 경계가 있는 3차원 물체의 체적 계산에 사용할 수 있다.2차원 영역의 면적은 앞서 언급한 확실한 ^[48]적분을 사용하여 계산할 수 있습니다.디스크나 와셔와 같은 3차원 물체의 부피는 실린더 부피의 방정식 $\pi r^{2}h$ r $\pi r^{2}h$ \ $displaystyle \pi$ r $^{2}h$ r\ $displaystyle$ r $}$ 는 $r$ 반지름)를 사용하여 디스크 적분으로 계산할 수 있습니다.x축에 대해 곡선을 회전시켜 작성한 단순 원반의 경우 반지름은 $f ($ x)로 하고 높이는 $차분$ dx이다. $경계$ $a$ 와 b가 있는 적분을 사용하면 디스크의 볼륨은 다음과 같습니다.^[49]

\pi \int _{a}^{b}f^{2}(x) ,

적분은 물리학과 같은 분야에서도 변위, 시간, 속도와 같은 양을 찾기 위해 사용됩니다.예를 들어 직선 운동에서 시간

[a,b]

간격 [

[a,b]

]

{

displaystyle [

a, b

]

{displaystyle [a,

[a,b]

b]}에

[a,b]

걸친 물체의 변위는 다음과 같이 구한다.

x(b)-x(a)=\int _{a}^{b}v(t),dt,

$v(t)$ 서 v $v(t)$ $)$ { $displaystyle$ v $(t)}$ 는 $v(t)$ 시간의 ^[50]함수로 표현되는 속도입니다. $F(x)$ $위치$ A(\ $displaystyle$ A $)$ 에서 $A$ 최종 $위치$ B $(\displaystyle$ B $)$ 까지 $B$ 힘 F $(x)($ 위치의 함수로 지정)에 의해 수행되는 작업은 다음과 같습니다.^[51]

W_{A\오른쪽 화살표 B}=\int _{A}^{B}F(x),dx

적분은 열역학에서도 사용되며, 열역학 적분은 두 주어진 상태 사이의 자유 에너지 차이를 계산하기 위해 사용됩니다.

계산

분석적

하나의 실변수의 확실한 적분을 계산하기 위한 가장 기본적인 기술은 미적분의 기본 정리에 기초한다.f $(x)$ 가 주어진 간격 $[a,$ $b]$ 에 걸쳐 적분되는 $x$ 의 함수라고 $하자$ .그런 다음 $f$ 의 역도함수, 즉 구간에서 Fθ = $f$ 가 $되는$ $함수$ F를 구합니다.적분과 적분이 통합의 경로에 특이점을 가지지 않는다면, 미적분의 기본 정리에 의해,

\displaystyle \int _{a}^{b}f(x),dx=F(b)-F(a)}

적분을 평가하기 위해 개발된 많은 기술 중 하나를 사용해야 할 경우가 있습니다.대부분의 이러한 기술은 하나의 적분을 다른 적분으로 고쳐 쓰는데, 이는 더 다루기 쉽기 때문입니다.기법은 치환에 의한 적분, 부품에 의한 적분, 삼각치환에 의한 적분 및 부분분수에 의한 적분을 포함한다.

보다 복잡한 적분을 계산하기 위한 대체 방법이 존재합니다.많은 비보조 적분들은 테일러 급수에서 확장될 수 있고 항별로 통합될 수 있다.때때로 결과 무한 급수를 분석적으로 합산할 수 있습니다.Meijer G 함수를 사용하는 컨볼루션 방법도 사용할 수 있는데, 이는 인테그랜드가 Meijer G 함수의 곱으로 작성될 수 있다고 가정할 수 있다.또한 한정된 적분을 계산하는 방법은 많이 있습니다. 예를 들어, Parseval의 항등식을 사용하여 직사각형 영역의 적분을 무한합으로 변환할 수 있습니다.때로는 트릭으로 적분을 평가할 수 있습니다. 이에 대한 예는 가우스 적분을 참조하십시오.

회전체의 볼륨 계산은 일반적으로 디스크 통합 또는 셸 통합을 사용하여 수행할 수 있습니다.

다양한 기술로 도출된 특정 결과는 적분 목록에 수집됩니다.

심볼릭

수학, 물리학 및 공학에서의 많은 문제들은 적분에 대한 명시적인 공식이 요구되는 부분적분을 포함한다.이 목적을 위해 수년간 광범위한 적분표가 작성되고 발행되었습니다.컴퓨터의 보급에 수반해, 많은 프로페셔널, 교육자, 및 학생은, 통합등의 어려운 작업이나 귀찮은 작업을 실행하도록 특별히 설계된 컴퓨터 대수 시스템에 눈을 돌리고 있습니다.상징적 통합은 맥시마나 메이플과 같은 최초의 시스템 개발 동기 중 하나이다.

기호 적분에서의 큰 수학적 어려움은 많은 경우에 비교적 단순한 함수는 유리함수와 지수함수, 로그, 삼각함수와 역삼각함수, 그리고 다중연산을 포함한 닫힌 형태로 표현될 수 있는 적분을 가지고 있지 않다는 것이다.설명 및 구성.Risch 알고리즘은 기본 함수의 역도함수가 기본인지 여부를 판단하고 기본 함수의 역도함수인 경우 이를 계산하기 위한 일반적인 기준을 제공합니다.그러나, 반미분 표현식의 닫힌 함수는 예외이며, 결과적으로 컴퓨터화된 대수 시스템은 무작위로 구성된 기본 함수에 대한 반미분 함수를 찾을 수 있을 것이라는 희망이 없다.긍정적인 측면에서는, 반파생물의 '구성 블록'을 미리 고정해 두면, 이러한 블록과 곱셈 및 구성의 연산을 사용하여 주어진 함수의 반파생물을 표현할 수 있는지 여부를 결정하고, 그것이 존재할 때마다 기호적인 답을 찾을 수 있을 것이다.Mathematica, Maple 및 기타 컴퓨터 대수 체계에서 구현된 Risch 알고리즘은 유리함수, 라디칼, 로그 및 지수함수에서 생성된 함수와 반미분함수에 대해서만 구현됩니다.

일부 특수 적분자는 특수 연구가 필요할 정도로 자주 발생합니다.특히 반파생물의 집합에서 특수 함수(예: Legendre 함수, 초기하 함수, 감마 함수, 불완전한 감마 함수 등)를 갖는 것이 유용할 수 있다.이러한 기능을 포함하도록 Risch의 알고리즘을 확장하는 것은 가능하지만 어려운 일이며 활발한 연구 주제였습니다.

최근에는 다항식 계수를 갖는 선형 미분 방정식의 해인 D-유한 함수를 사용하는 새로운 접근법이 등장했다.기본 및 특수 함수의 대부분은 D-유한이며, D-유한 함수의 적분도 D-유한 함수이다.이것은 D-유한함수의 반미분을 미분방정식의 해로 표현하기 위한 알고리즘을 제공한다.이 이론은 또한 D-함수의 확실한 적분을 첫 번째 계수에 의해 주어진 급수의 합으로 계산할 수 있게 하고, 어떤 계수를 계산하기 위한 알고리즘을 제공한다.

숫자

수치직교법: 직사각형법, 사다리꼴규칙, 롬버그법, 가우스직교법

확실한 적분은 몇 가지 수치 적분 방법을 사용하여 근사할 수 있다.직사각형 방법은 함수 아래의 영역을 함수 값에 해당하는 일련의 직사각형으로 나누고 합계를 구하기 위해 단계 너비를 곱합니다.더 나은 접근법인 사다리꼴 법칙은 리만 합계에서 사용되는 직사각형을 사다리꼴로 대체합니다.사다리꼴 규칙은 첫 번째 값과 마지막 값의 가중치를 1/2로 지정한 다음 단계 폭에 곱하여 더 나은 ^[52]근사치를 얻습니다.함수에 대한 보다 정확한 근사치가 적분에 대한 더 나은 근사치를 산출한다는 사다리꼴 법칙 뒤에 있는 아이디어는 더 나아가서 전달될 수 있다: 심슨의 법칙은 부분적인 2차 ^[53]함수에 의해 적분과 근사한다.

리만 합, 사다리꼴 법칙, 심슨 법칙은 뉴턴-코츠 공식이라고 불리는 직교 규칙군의 예입니다. $정도$ n 뉴턴-코츠 직교 규칙은 $각$ 부분 구간에 대한 다항식을 정도 n 다항식으로 근사한다.이 다항식은 ^[54]구간에 함수 값을 보간하기 위해 선택됩니다.더 높은 차수의 뉴턴-코츠 근사치는 더 정확할 수 있지만, 더 많은 함수 평가가 필요하며, 룽지 현상으로 인해 수치적 부정확성에 시달릴 수 있습니다.이 문제에 대한 한 가지 해결책은 클렌쇼-커티스 직교로, 적분자는 체비셰프 다항식의 관점에서 확장하여 근사한다.

Romberg의 방법은 스텝 폭을 증분적으로 반으로 줄여 T $(h 0),$ $T (h 1)$ $등$ 으로 표시된 사다리꼴 근사치를 제공합니다. $여기$ 서_k+1 h는 $h$ 의_k 절반입니다.각 새 단계 크기에 대해 새 함수 값의 절반만 계산하면 되고, 나머지 값은 이전 크기에서 이월됩니다.그런 다음 근사치를 통해 다항식을 보간하고 T( $0)$ 로 추정한다.가우스 직교 다항식 ^[55]집합의 루트에서 함수를 평가합니다. $n점$ 가우스 $방법$ 은 최대 2n - 1의 다항식에 대해 정확하다.

고차원 적분(예: 체적 계산)의 계산은 몬테카를로 적분(Monte Carlo ^[56]integration)과 같은 대안을 중요하게 이용한다.

기계

임의의 2차원 형상의 면적은 평면계라고 불리는 측정기를 사용하여 측정할 수 있습니다.불규칙한 물체의 부피는 물체가 물에 잠길 때 변위된 유체로 정확하게 측정할 수 있습니다.

기하학적

면적은 때때로 동등한 정사각형의 기하학적 나침반과 직선 구조를 통해 찾을 수 있다.

차별화에 의한 통합

Kempf, Jackson 및 Morales는 미분을 통해 적분을 계산할 수 있는 수학적 관계를 입증했다.이들의 미적분에는 Dirac 델타 함수와 편미분 연산자 $\partial _{x}$ x ${\displaystyle$ \ $partial _{$ x $\partial _{x}$ 가 포함된다.이것은 함수 적분에도 적용할 수 있기 때문에 함수 ^[57]미분에도 적용할 수 있다.

예

미적분의 기본정리를 이용하다

미적분의 기본정리는 기본함수의 간단한 계산을 가능하게 한다.

$\displaystyle \int _{0}^{\pi }\sin(x)\mid _{x=0}^{x=\pi }=-\cos(\pi)-(-\cos(0)=2}$

「」를 참조해 주세요.

적분 방정식 – 적분 기호 아래에 알 수 없는 함수가 있는 방정식
적분 기호 – 적분 및 반미분을 나타내기 위해 사용되는 수학 기호

메모들

^ 적분학은 많은 출처가 있는 매우 확립된 수학 분야이다.예를 들어 Apostol 1967 및 Anton, Bivens & Davis 2016을 참조하십시오.

레퍼런스

^ 버튼 2011, 페이지 117
^ 2002년 히스
^ Katz 2009, 페이지 201-204.
^ Katz 2009, 284–285페이지.
^ Katz 2009, 페이지 305-306.
^ Katz 2009, 페이지 516-517.
^ Struik 1986, 페이지 215~216.
^ Katz 2009, 페이지 536-537.
^ 버튼 2011, 페이지 385-386.
^ 그래도 1989년, 131페이지
^ Katz 2009, 페이지 628-629.
^ Katz 2009, 페이지 785
^ 버튼 2011, 페이지 414; 라이프니츠 1899, 페이지 154.
^ 카조리 1929, 페이지 249–250; 푸리에 1822, §231.
^ 카조리 1929, 페이지 246
^ 카조리 1929, 페이지 182
^ ^a ^b 아포톨 1967, 74페이지
^ 안톤, 비븐스 & 데이비스 2016, 페이지 259
^ 아포톨 1967, 페이지 69
^ 안톤, 비븐스 & 데이비스 2016, 286-287페이지.
^ 크랜츠 1991, 페이지 173
^ 1987년 루딘, 5페이지
^ Siegmund-Schultze 2008, 페이지 796
^ 폴랜드 1999, 페이지 57-58.
^ 부르바키 2004, 페이지 IV.43
^ Lieb & Loss 2001, 페이지 14
^ 1999년, 53페이지
^ ^a ^b 루딘 1987, 페이지 25
^ ^a ^b 아포톨 1967, 페이지 80
^ 루딘 1987, 54페이지
^ 아포톨 1967, 페이지 81
^ ^a ^b 루딘 1987, 페이지 63
^ 아포톨 1967, 페이지 202
^ 아포톨 1967, 페이지 205
^ 아포톨 1967, 페이지 416
^ 아포톨 1967, 페이지 418
^ 안톤, 비븐스 & 데이비스 2016, 페이지 895
^ ^a ^b 안톤, 비븐스 & 데이비스 2016, 페이지 896
^ 안톤, 비븐스 & 데이비스 2016, 페이지 897
^ 안톤, 비븐스 & 데이비스 2016, 980페이지
^ 안톤, 비븐스 & 데이비스 2016, 981페이지
^ 안톤, 비븐스 & 데이비스 2016, 페이지 697
^ 안톤, 비븐스 & 데이비스 2016, 991페이지
^ Anton, Bivens & Davis 2016, 페이지 1014.
^ 안톤, 비븐스 & 데이비스 2016, 페이지 1024
^ 펠러 1966, 페이지 1
^ 펠러 1966, 3페이지
^ 아포톨 1967, 페이지 88~89
^ 아포톨 1967, 페이지 111~114
^ 안톤, 비븐스 & 데이비스 2016, 페이지 306
^ 아포톨 1967, 페이지 116
^ Dahlquist & Björck 2008, 페이지 519-520.
^ Dahlquist & Björck 2008, 페이지 522-524.
^ Kahaner, Moler & Nash 1989, 페이지 144
^ Kahaner, Moler & Nash 1989, 페이지 147
^ Kahaner, Moler & Nash 1989, 139-140페이지.
^ Kempf 2015 harvnb 오류: 대상 없음: CITREFKempf2015(도움말)

참고 문헌

Anton, Howard; Bivens, Irl C.; Davis, Stephen (2016), Calculus: Early Transcendentals (11th ed.), John Wiley & Sons, ISBN 978-1-118-88382-2
Apostol, Tom M. (1967), Calculus, Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra (2nd ed.), Wiley, ISBN 978-0-471-00005-1
특히 III장 및 IV장Bourbaki, Nicolas (2004), Integration I, Springer-Verlag, ISBN 3-540-41129-1.
Burton, David M. (2011), The History of Mathematics: An Introduction (7th ed.), McGraw-Hill, ISBN 978-0-07-338315-6
Cajori, Florian (1929), A History Of Mathematical Notations Volume II, Open Court Publishing, ISBN 978-0-486-67766-8
Dahlquist, Germund; Björck, Åke (2008), "Chapter 5: Numerical Integration", Numerical Methods in Scientific Computing, Volume I, Philadelphia: SIAM, archived from the original on 2007-06-15
Feller, William (1966), An introduction to probability theory and its applications, John Wiley & Sons
Folland, Gerald B. (1999), Real Analysis: Modern Techniques and Their Applications (2nd ed.), John Wiley & Sons, ISBN 0-471-31716-0
Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur, Chez Firmin Didot, père et fils, p. §231
번역으로 제공되다
Heath, T. L., ed. (2002), The Works of Archimedes, Dover, ISBN 978-0-486-42084-4
(원래는 1897년 케임브리지 대학 출판부에서 발행한 것으로, J. L. 하이버그의 그리스어 버전에 근거하고 있습니다.)
Hildebrandt, T. H. (1953), "Integration in abstract spaces", Bulletin of the American Mathematical Society, 59 (2): 111–139, doi:10.1090/S0002-9904-1953-09694-X, ISSN 0273-0979
Kahaner, David; Moler, Cleve; Nash, Stephen (1989), "Chapter 5: Numerical Quadrature", Numerical Methods and Software, Prentice Hall, ISBN 978-0-13-627258-8
Kallio, Bruce Victor (1966), A History of the Definite Integral (PDF) (M.A. thesis), University of British Columbia, archived from the original (PDF) on 2014-03-05, retrieved 2014-02-28
Katz, Victor J. (2009), A History of Mathematics: An Introduction, Addison-Wesley, ISBN 978-0-321-38700-4
Kempf, Achim; Jackson, David M.; Morales, Alejandro H. (2015), "How to (path-)integrate by differentiating", Journal of Physics: Conference Series, [[]], 626 (1): 012015, arXiv:1507.04348, Bibcode:2015JPhCS.626a2015K, doi:10.1088/1742-6596/626/1/012015, S2CID 119642596
Krantz, Steven G. (1991), Real Analysis and Foundations, CRC Press, ISBN 0-8493-7156-2
Leibniz, Gottfried Wilhelm (1899), Gerhardt, Karl Immanuel (ed.), Der Briefwechsel von Gottfried Wilhelm Leibniz mit Mathematikern. Erster Band, Berlin: Mayer & Müller
Lieb, Elliott; Loss, Michael (2001), Analysis, Graduate Studies in Mathematics, vol. 14 (2nd ed.), American Mathematical Society, ISBN 978-0821827833
Rudin, Walter (1987), "Chapter 1: Abstract Integration", Real and Complex Analysis (International ed.), McGraw-Hill, ISBN 978-0-07-100276-9
Saks, Stanisław (1964), Theory of the integral (English translation by L. C. Young. With two additional notes by Stefan Banach. Second revised ed.), New York: Dover
를 클릭합니다Siegmund-Schultze, Reinhard (2008), "Henri Lebesgue", in Timothy Gowers; June Barrow-Green; Imre Leader (eds.), Princeton Companion to Mathematics, Princeton University Press, ISBN 978-0-691-11880-2.
Stillwell, John (1989), Mathematics and Its History, Springer, ISBN 0-387-96981-0
를 클릭합니다Stoer, Josef; Bulirsch, Roland (2002), "Topics in Integration", Introduction to Numerical Analysis (3rd ed.), Springer, ISBN 978-0-387-95452-3.
Struik, Dirk Jan, ed. (1986), A Source Book in Mathematics, 1200-1800, Princeton, New Jersey: Princeton University Press, ISBN 0-691-08404-1
W3C (2006), Arabic mathematical notation

외부 링크

"Integral", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
온라인 적분 계산기, 울프램 알파

온라인 서적

키슬러, H. 제롬, 초등 미적분: 위스콘신 대학교 무한소수를 이용한 접근법
Stroyan, K. D., 아이오와 대학교 무한소수 미적분 개요
미적분학을 완벽하게 소개하는 온라인 교과서인 Mauch, Sean, Sean's Applied Math Book, CIT
Crowell, Benjamin, 미적분, Fullerton College, 온라인 교과서
개럿, 폴, 1학년 미적분 노트
온라인 교과서인 후세인, 파라즈, 미적분 이해
Johnson, William Woolsey(1909) 적분학 초등 논문, HathiTrust 링크.
올덴부르크 대학 통합이론, 코월크, W.P.오래된 문제에 대한 새로운 개념.온라인 교과서
Slouter, Dan, 미분방정식에 대한 차분방정식, 미적분 입문
총체적 수치법 연구소의 수치적분법
P. S. Wang, 기호조작에 의한 확정적분평가(1972) - 확정적분기술의 요리책

[1] 적분학은 많은 출처가 있는 매우 확립된 수학 분야이다.예를 들어 Apostol 1967 및 Anton, Bivens & Davis 2016을 참조하십시오.

[2] 버튼 2011, 페이지 117

[3] 2002년 히스

[4] Katz 2009, 페이지 201-204.

[5] Katz 2009, 284–285페이지.

[6] Katz 2009, 페이지 305-306.

[7] Katz 2009, 페이지 516-517.

[8] Struik 1986, 페이지 215~216.

[9] Katz 2009, 페이지 536-537.

[10] 버튼 2011, 페이지 385-386.

[11] 그래도 1989년, 131페이지

[12] Katz 2009, 페이지 628-629.

[13] Katz 2009, 페이지 785

[14] 버튼 2011, 페이지 414; 라이프니츠 1899, 페이지 154.

[15] 카조리 1929, 페이지 249–250; 푸리에 1822, §231.

[16] 카조리 1929, 페이지 246

[17] 카조리 1929, 페이지 182

[:1-18] 아포톨 1967, 74페이지

[19] 안톤, 비븐스 & 데이비스 2016, 페이지 259

[20] 아포톨 1967, 페이지 69

[21] 안톤, 비븐스 & 데이비스 2016, 286-287페이지.

[22] 크랜츠 1991, 페이지 173

[23] 1987년 루딘, 5페이지

[24] Siegmund-Schultze 2008, 페이지 796

[25] 폴랜드 1999, 페이지 57-58.

[26] 부르바키 2004, 페이지 IV.43

[27] Lieb & Loss 2001, 페이지 14

[28] 1999년, 53페이지

[:3-29] 루딘 1987, 페이지 25

[:0-30] 아포톨 1967, 페이지 80

[31] 루딘 1987, 54페이지

[32] 아포톨 1967, 페이지 81

[:4-33] 루딘 1987, 페이지 63

[34] 아포톨 1967, 페이지 202

[35] 아포톨 1967, 페이지 205

[36] 아포톨 1967, 페이지 416

[37] 아포톨 1967, 페이지 418

[38] 안톤, 비븐스 & 데이비스 2016, 페이지 895

[:2-39] 안톤, 비븐스 & 데이비스 2016, 페이지 896

[40] 안톤, 비븐스 & 데이비스 2016, 페이지 897

[41] 안톤, 비븐스 & 데이비스 2016, 980페이지

[42] 안톤, 비븐스 & 데이비스 2016, 981페이지

[43] 안톤, 비븐스 & 데이비스 2016, 페이지 697

[44] 안톤, 비븐스 & 데이비스 2016, 991페이지

[45] Anton, Bivens & Davis 2016, 페이지 1014.

[46] 안톤, 비븐스 & 데이비스 2016, 페이지 1024

[47] 펠러 1966, 페이지 1

[48] 펠러 1966, 3페이지

[49] 아포톨 1967, 페이지 88~89

[50] 아포톨 1967, 페이지 111~114

[51] 안톤, 비븐스 & 데이비스 2016, 페이지 306

[52] 아포톨 1967, 페이지 116

[53] Dahlquist & Björck 2008, 페이지 519-520.

[54] Dahlquist & Björck 2008, 페이지 522-524.

[55] Kahaner, Moler & Nash 1989, 페이지 144

[56] Kahaner, Moler & Nash 1989, 페이지 147

[57] Kahaner, Moler & Nash 1989, 139-140페이지.

[58] Kempf 2015 harvnb 오류: 대상 없음: CITREFKempf2015(도움말)

[a]

[1]

[2]

[3]

[4]

[5]

[7]

[6]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[56]

[57]

v t 통합
인테그레이션의 종류	리만 적분 르베그 적분 버킬 적분 보히너 적분 다니엘 적분 다르부 적분 헨스톡-쿠르즈와일 적분 Haar 적분 헬링거 적분 킨친 적분 콜모고로프 적분 르베그-슈티엘트제 적분 페티스 적분 페퍼 적분 리만-슈틸테스의 적분 규제적분
통합 기술	대체 삼각법 오일러 바이어스트라스 부품별 부분 분수 오일러 공식 역함수 순서 변경 환원식 파라메트릭 도함수 적분 기호 아래의 차별화 라플라스 변환 등고선 통합 라플라스법 수치 적분 심슨의 법칙 사다리꼴 규칙 라이시 알고리즘
부적절한 통합	가우스 적분 디리클레 적분 페르미-디락 적분 완성하다 불완전 보스-아인슈타인 적분 프룰라니 적분 양자장 이론의 공통 적분
확률적분	이토 적분 루소-발루아 적분 스트라토노비치 적분 스코로호트 적분
여러가지 종류의	바젤 문제 오일러-마클로린 공식 가브리엘의 뿔 인테그레이션 22/7이 †를 초과하는 증거 볼륨 세탁기 셸

v t 수학 분석의 주요 주제
미적분:통합 차별화 미분 방정식(일반 - 부분 - 확률적) 미적분의 기본 정리 변분법 벡터 미적분 텐서 미적분 행렬 미적분 적분 목록 파생상품표
실제 분석 복잡한 분석 초복소 분석 (4분위 분석) 기능 분석 푸리에 분석 최소 제곱 스펙트럼 분석 고조파 분석 P-adic 분석(P-adic 수) 측정 이론 표현 이론 기능들 연속 함수 특수 기능 제한. 시리즈 Infinity
수학 포털

Search

일체형

역사