롤의 정리
Rolle's theorem| 에 대한 일련의 기사의 일부 |
| 미적분학. |
|---|

미적분학에서 롤의 정리 또는 롤의 보조정리는 본질적으로 두 개의 다른 점에서 동일한 값을 얻는 실수 값 미분 가능 함수는 그들 사이에 적어도 하나의 정지점, 즉 첫 번째 도함수(함수의 그래프에 대한 접선의 기울기)가 0인 점을 가져야 한다는 것을 말합니다. 이 정리는 미셸 롤의 이름을 따서 지어졌습니다.
정리의 표준 버전
실제 값 함수 f가 열린 구간 (a, b)에서 미분 가능한 적절한 닫힌 구간 [a, b]에서 연속적인 경우, 열린 구간 (a, b)에 적어도 하나의 c가 존재하며, 이는 다음과 같습니다.
이 버전의 롤 정리는 평균값 정리를 증명하는 데 사용되며, 그 중 롤 정리는 실제로 특별한 경우입니다. 테일러 정리의 증명의 기초가 되기도 합니다.
역사
이 정리는 미셸 롤의 이름을 따서 명명되었지만, 롤의 1691년 증명은 다항 함수의 경우만 다루었습니다. 그의 증명은 미분적분학의 방법을 사용하지 않았으며, 그 당시 그는 그의 삶에서 잘못된 것으로 여겼습니다. 이 정리는 평균값 정리의 증명의 결과로서 1823년 코시에 의해 처음으로 증명되었습니다.[1] "롤의 정리"라는 이름은 1834년 독일의 모리츠 빌헬름 드로비슈와 1846년 이탈리아의 주스토 벨라비티스에 의해 처음 사용되었습니다.[2]
예
첫번째 예
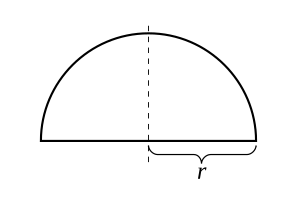
반지름 r > 0인 경우 함수를 고려합니다.
그래프는 원점을 중심으로 한 위쪽 반원입니다. 이 함수는 닫힌 구간 [-r, r]에서 연속적이고 열린 구간 (-r, r)에서는 미분할 수 있지만 끝점 -r 및 r에서는 미분할 수 없습니다. f(-r) = f(r)이므로 롤의 정리가 적용되며 실제로 f의 도함수가 0인 점이 있습니다. 이 정리는 열린 구간에서 함수를 미분할 수 있어야 하기 때문에 끝점에서 함수를 미분할 수 없는 경우에도 적용됩니다.
두번째 예

구간의 내부 지점에서 미분이 실패하면 롤 정리의 결론이 성립하지 않을 수 있습니다. 절댓값 함수를 고려합니다.
그러면 f(-1) = f(1)이지만 -1과 1 사이에 f'(c)가 0인 c는 없습니다. 그 함수는 연속적이기는 하지만 x = 0에서 미분할 수 없기 때문입니다. 도함수 f는 x = 0에서 부호가 변하지만 값 0은 되지 않습니다. 이 정리는 열린 구간의 모든 x에 대해 함수가 미분 가능해야 한다는 조건을 만족하지 않기 때문에 이 함수에 적용할 수 없습니다. 그러나 미분가능성 요건이 롤의 정리에서 떨어졌을 때 f는 열린 구간(a, b)에서 여전히 임계수를 갖지만 (그래프에 표시된 절대값의 경우와 같이) 수평 접선을 산출하지 못할 수 있습니다.
일반화
두 번째 예는 롤 정리의 다음과 같은 일반화를 보여줍니다.
f(a) = f(b)인 닫힌 구간 [a, b]에 대한 실수 값 연속 함수 f를 생각해 보십시오. 열린 구간 (a, b)의 모든 x에 대하여 오른쪽 극한
확장된 실수선 [- ∞, ∞]에 존재하며, 열린 구간 (a, b)에 어떤 수 c가 존재하여 두 극한 중 하나가 존재합니다.
언급
- f가 볼록하거나 오목한 경우, 오른쪽 도함수와 왼쪽 도함수는 모든 내부점에 존재하므로 위의 극한은 존재하며 실수입니다.
- 이 정리의 일반화된 버전은 편면 도함수가 단조적으로 증가할 때 볼록성을 증명하기에 충분합니다.[3]
일반화된 버전의 증명
롤의 정리의 표준 버전과 일반화에 대한 증명은 매우 유사하므로 일반화를 증명합니다.
증명의 아이디어는 만약 f (a) = f (b)이면, f는 a와 b 사이의 어딘가에서, 예를 들어 c에서 최댓값 또는 최솟값에 도달해야 하며, 함수는 c에서 증가에서 감소로(또는 반대로) 변화해야 한다고 주장하는 것입니다. 특히 도함수가 존재하는 경우 c에서 0이어야 합니다.
가정에 따라 f는 [a, b]에서 연속적이며 극값 정리에 의해 [a, b]에서 최대값과 최소값을 모두 얻을 수 있습니다. 이것들이 모두 [a, b]의 끝점에서 얻어지면 f는 [a, b]에서 일정하므로 f의 도함수는 (a, b)의 모든 점에서 0입니다.
그렇다면 (a, b)의 내부점 c에서 최댓값을 구한다고 가정합니다(최솟값에 대한 인수는 매우 유사하므로 -f를 고려하십시오). 위와 같은 좌우 한계를 구분하여 살펴보기로 합니다.
[a, b]에서 c + h가 되는 실제 h의 경우, f (c + h) 값은 c에서 최대치를 유지하기 때문에 f (c)보다 작거나 같습니다. 따라서 매 시간 > 0일 때마다,
마찬가지로 모든 h < 0일 때, 분모가 음수이기 때문에 부등식이 역전됩니다.
마지막으로, 위의 오른쪽 한계와 왼쪽 한계가 일치하는 경우(특히 f가 미분 가능한 경우), f 의 도함수는 0이어야 합니다.
(또는 페르마의 정지점 정리를 직접 적용할 수도 있습니다.)
상위 도함수에 대한 일반화
우리는 또한 f가 같은 값과 더 큰 규칙성을 가진 더 많은 점을 가질 것을 요구함으로써 롤의 정리를 일반화할 수 있습니다. 구체적으로, 다음과 같은 경우
- 함수 f는 닫힌 구간 [a, b]에서 연속적으로 미분 가능하며 n번째 도함수는 열린 구간 (a, b)에서 존재하며,
- [a, b]에는 1부터 n까지의 k마다 f(a) = f(b)가 되도록 a < b ≤ a < b ≤ a ⋯ ≤ a < b로 주어진 n개의 간격이 있습니다.
그러면 fat c의 n차 도함수가 0이 되도록 cin (a, b)라는 숫자가 있습니다.
f 대신 위에서 정의한 오른쪽 및 왼쪽 한계에 대한 상응하는 (아마도 더 약한) 주장을 제공함으로써, n번째 도함수 f에 관한 요건은 위의 일반화에서와 같이 약화될 수 있습니다.
특히, 이 정리의 버전은 충분히 미분 가능한 함수가 n개의 근(즉, 동일한 값, 즉 0)을 가지면 f가 사라지는 내부 점이 있다고 주장합니다.
증명
증명은 수학적 귀납법을 사용합니다. 경우 n = 1은 단순히 롤의 정리의 표준 버전입니다. n > 1의 경우 일반화가 n - 1에 대해 참이라는 귀납 가설을 가정합니다. 우리는 그것을 n에 대해 증명하고 싶습니다. 함수 f가 정리의 가설을 만족시킨다고 가정합니다. 롤 정리의 표준 버전에 의해, 1부터 n까지의 모든 정수 k에 대하여, 열린 구간 (a, b)에 f'(c) = 0이 되는 c가 존재합니다. 따라서, 1차 도함수는 n - 1개의 닫힌 구간 [c, c], …, [c, c]에 대한 가정을 만족합니다. 귀납 가설에 의해 c에서 f'의 (n - 1)번째 도함수가 0이 되는 c가 존재합니다.
다른 필드에 대한 일반화
롤의 정리는 순서 필드인 실수에 대한 미분 가능한 함수의 성질입니다. 따라서 다른 분야에 일반화하지는 않지만 다음과 같은 결과가 나옵니다. 실수 위에 모든 근을 갖는 실수 다항식 인자가 있으면 그 도함수도 마찬가지입니다. 누군가는 이 속성을 필드 롤의 속성이라고 부를 수 있습니다.[citation needed] 더 일반적인 필드는 항상 미분 가능한 함수를 가지는 것은 아니지만 항상 다항식을 가지므로 기호적으로 미분할 수 있습니다. 마찬가지로 더 일반적인 필드에는 순서가 없을 수 있지만 필드에 놓여 있는 다항식의 근에 대한 개념이 있습니다.
따라서 롤의 정리는 실수가 롤의 성질을 갖는다는 것을 보여줍니다. 복소수와 같이 대수적으로 닫힌 필드는 모두 롤의 성질을 갖습니다. 그러나 유리수는 유리수보다 x - x = x (x - 1) (x + 1) 인자가 아니라 그 도함수,
복잡한 버전은 부르호브 인덱스를 참조하십시오.
참고 항목
참고문헌
- ^ Besenyei, A. (September 17, 2012). "A brief history of the mean value theorem" (PDF).
- ^ 참조
- ^ Artin, Emil (1964) [1931], The Gamma Function, translated by Butler, Michael, Holt, Rinehart and Winston, pp. 3–4
- ^ Kaplansky, Irving (1972), Fields and Rings
- ^ Craven, Thomas; Csordas, George (1977), "Multiplier sequences for fields", Illinois J. Math., 21 (4): 801–817, doi:10.1215/ijm/1256048929
- ^ Ballantine, C.; Roberts, J. (January 2002), "A Simple Proof of Rolle's Theorem for Finite Fields", The American Mathematical Monthly, Mathematical Association of America, 109 (1): 72–74, doi:10.2307/2695770, JSTOR 2695770
더보기
- Leithold, Louis (1972). The Calculus, with Analytic Geometry (2nd ed.). New York: Harper & Row. pp. 201–207. ISBN 0-06-043959-9.
- Taylor, Angus E. (1955). Advanced Calculus. Boston: Ginn and Company. pp. 30–37.
외부 링크
- "Rolle theorem", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- 롤과 평균값 정리는 잘린 상태에서 계산됩니다.
- Mizar 시스템 프루프: http://mizar.org/version/current/html/rolle.html#T2

![{\displaystyle f(x)={\sqrt {r^{2}-x^{2}}},\quad x\in [-r,r].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7ef1f348169f09e9db96b68d4b2e73d5f43c156)
![{\displaystyle f(x)=|x|,\qquad x\in [-1,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/106570318bb857ac95a60c075c30a0f40dde84fe)










