수학에서 아우구스틴루이 코치의 이름을 딴 코치 응축시험은 무한계열의 표준 융합시험이다. For a non-increasing sequence  of non-negative real numbers, the series
of non-negative real numbers, the series  converges if and only if the "condensed" series }f 수렴
converges if and only if the "condensed" series }f 수렴 . 더욱이 이들이 수렴하면 응축된 계열의 합은 원형의 합보다 2배 이상 크지 않다.
. 더욱이 이들이 수렴하면 응축된 계열의 합은 원형의 합보다 2배 이상 크지 않다.
견적
코치 응축 시험은 더 강한 추정치로부터 따른다.

연장된 실수의 불평등으로 이해되어야 한다. 어떤 증거의 본질적인 추력은 조화 계열의 분리에 대한 오레스메의 증거를 본떠서 만든 것이다.
첫 번째 불평등을 보기 위해, 원래 시리즈의 조건을 두 개의 힘이 있는 런으로 다시 분류한 다음, 각 런을 해당 런에서 가장 큰 기간으로 교체하여 위에 경계를 정한다. 그 용어는 항상 첫 번째 용어가 된다. 왜냐하면 용어는 증가하지 않아야 하기 때문이다.

To see the second inequality, these two series are again rebracketed into runs of power of two length, but "offset" as shown below, so that the run of  which begins with
which begins with  lines up with the end of the run of =0 ( ) (로 끝나는
lines up with the end of the run of =0 ( ) (로 끝나는 (n은 f () n
(n은 f () n 로 끝나므로 전자는 항상 후자의 "so"이다.
로 끝나므로 전자는 항상 후자의 "so"이다.

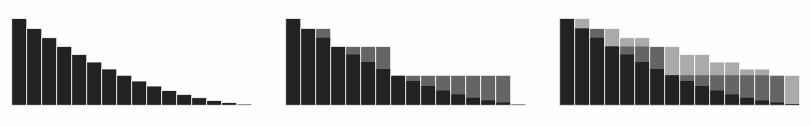
위 인수의 시각화. 시리즈  f ( ){\
f ( ){\ 의 부분 합계가
의 부분 합계가 왼쪽에서 오른쪽으로 겹쳐 보인다.
왼쪽에서 오른쪽으로 겹쳐 보인다. 적분비교
The "condensation" transformation  recalls the integral variable substitution
recalls the integral variable substitution  yielding f(e^{ {}x
yielding f(e^{ {}x 
Pursuing this idea, the integral test for convergence gives us, in the case of monotone  , that
, that  converges if and only if
converges if and only if  converges. The substitution
converges. The substitution  yields the integral
yields the integral  . We then notice that 어디의 오른쪽 편은 농축된 시리즈에 따른 적분 판정 법을 적용하는 ∑ nx0∞ 2n.에서 나온다 E\displaystyle \log 2\\int _{2}^{\infty}\!2^ᆭf(2^{x})\,\mathrm{d}x}<>로그 f(2))d2∫ 0∞ 2)){\displaystyle\displaystyle \log 2\ \int_{0}^{\infty}\!2^ᆱf(2^{x})\,\mathrm{d}x}, f() \sum \
. We then notice that 어디의 오른쪽 편은 농축된 시리즈에 따른 적분 판정 법을 적용하는 ∑ nx0∞ 2n.에서 나온다 E\displaystyle \log 2\\int _{2}^{\infty}\!2^ᆭf(2^{x})\,\mathrm{d}x}<>로그 f(2))d2∫ 0∞ 2)){\displaystyle\displaystyle \log 2\ \int_{0}^{\infty}\!2^ᆱf(2^{x})\,\mathrm{d}x}, f() \sum \ . Therefore,
. Therefore,  converges if and only if
converges if and only if  converges.
converges.
예
이 테스트는 n이 f의 분모처럼 나타나는 시리즈에 유용할 수 있다. 이러한 종류의 가장 기본적인 예에 대해 고조파 시리즈= ∞ / n \sum 은(는) 시리즈 1 \ 로 변환되어
로 변환되어 분명히 구분된다.
분명히 구분된다.
좀 더 복잡한 예로,
- ( ) n - n)- b n)- n

여기서 시리즈는 확실히 a > 1로 수렴되고, < 1로 전환된다. a = 1일 때 응축 변환은 연속된 열을 제공한다.
- - )- c n n

로그는 '좌측으로 이동'한다. 그래서 a = 1일 때 우리는 b > 1, b < 1에 대한 수렴을 가진다. b = 1이면 c의 값이 입력된다.
이 결과는 쉽게 일반화된다: 반복적으로 적용되는 응축 테스트를 사용하여 = 1,,…에 대해 일반화된 베르트랑 시리즈인 을 를) 보여줄 수 있다.
를) 보여줄 수 있다.

> 에 대한 수렴과 < 0 1에 대한 분산
< 0 1에 대한 분산 [1] 여기서 함수 의 m번째 합성 반복을 나타낸다
[1] 여기서 함수 의 m번째 합성 반복을 나타낸다


합계의 하한인 을 를) 선택하여 시리즈의 모든 항이 양수되도록 했다. 특히 이들 시리즈는 임의로 천천히 수렴하거나 이탈하는 무한대의 총액의 예를 제공한다. 예를 들어 = k
를) 선택하여 시리즈의 모든 항이 양수되도록 했다. 특히 이들 시리즈는 임의로 천천히 수렴하거나 이탈하는 무한대의 총액의 예를 제공한다. 예를 들어 = k = 1 의 경우
= 1 의 경우 부분 합은 10
부분 합은 10  구골플렉스) 항 후에만 10을 초과하지만 그럼에도 불구하고 시리즈는 서로 다르다.
구골플렉스) 항 후에만 10을 초과하지만 그럼에도 불구하고 시리즈는 서로 다르다.
u(n)는 연속적인 차이의 비율이 경계되도록 엄격히 증가되는 양의 정수 순서가 되도록 하라[2]: 다음을 위해 양의 실제 숫자 N이 있다.

다음, (n ) {\이(가) Cauchy의 테스트에서와 동일한 전제조건을 충족한다면 , 시리즈 ){\의 수렴은
, 시리즈 ){\의 수렴은 다음과 같다.
다음과 같다.

Taking  so that
so that  , the Cauchy condensation test emerges as a special case.
, the Cauchy condensation test emerges as a special case.
참조
외부 링크







 (n은 f (
(n은 f (