기하 급수

수학에서 기하계열은 연속된 항 사이에 일정한 비율을 갖는 무한한 수의 항을 합한 것이다. 예를 들어, 영상 시리즈

${\displaystyle {\frac {1}{1}:{2}}:\,+\,{\frac {1}{4}\,+\,{\frac {1}{8}\,+\,{\frac {1}{16}\,+\,\cdots }}$

각각의 연속된 용어는 전기에 1/2을 곱하여 얻을 수 있기 때문에 기하학이다. 일반적으로 기하계열은 + ar + ar² + ar³ + ar + ...로 표기되는데, 여기서 a는 각 항의 계수이고 r은 인접 항간의 공통 비율이다. 기하 시리즈는 무한 시리즈 중 가장 단순한 예에 속하며, 테일러 시리즈와 푸리에 시리즈에 대한 기본적인 소개 역할을 할 수 있다. 기하계열은 미적분의 초기 발달에 중요한 역할을 했고 수학 전반에 걸쳐 사용되고 물리학, 공학, 생물학, 경제학, 컴퓨터 과학, 대기열 이론, 금융에 중요한 응용 분야를 가지고 있다.

진행과 연속의 구별은 진행은 순서인 반면, 연속은 합이라는 것이다.

계수 a

기하 급수 a + ar + ar² + ar³ + ar + ... 확장된 형태로 쓰여 있다.^[1] 기하학 계열의 모든 계수는 같다. 이와는 대조적으로 파워 시리즈는₀₁ + 아₂² + 아 + 아₃³ + 아 + 아 + ...로 쓰여졌다. 확장형에는 항에 따라 다를 수 있는 계수 a가_i 있다. 즉, 기하계열은 파워계열의 특수한 경우라는 것이다. 확장된 형태의 기하학적 시리즈의 첫 번째 용어는 그 기하학적 시리즈의 계수 a이다.

기하계열의 확장형식 외에, 기하계열의 발전형식도^[1] 있다.

${\displaystyle \sum _{k=0}^{\inful }}}}$ ar^k

그리고 닫힌 형태의 기하학적 시리즈는 다음과 같이 쓰여졌다.

a / (1 - r) r < 1 범위 이내

확장형에서 폐쇄형식의 파생은 이 글의 Sum 섹션에 나와 있다. 파생은 자기 유사성을 이용하고, 확장된 형태의 추가 및 전원 연산의 무한 횟수를 폐쇄형식의 단일 뺄셈과 단일 분할로 줄이기 위해 시리즈의 모든 계수가 동일해야 한다(동효율 a). 그러나 그러한 파생이 없어도 그 결과는 긴 나눗셈으로 확인할 수 있다: (1 - r)로 나누면 기하계열의 확장형식인 + ar + ar² + ar + .....가³ 된다.

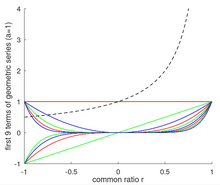
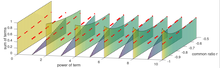
전형적으로 기하학 계열은 숫자 a + ar + ar² + ar³ + ar + ...의 합으로 생각된다. 그러나 함수 a + ar + ar² + ar + ar³ + ar + ...의 합으로도 생각할 수 있다. r < 1 범위 내에서 / (1 - r) 함수로 수렴한다. 그 인접한 이미지, 1일부터 a=1. 심지어 무엇이든 계수 이외는 계수의(파워 시리즈에 등비 수열을 바꾸는 것 외에)기능의 결과 금액을 바꿀 수 있다는 것을 바꾸는 것에 대한 첫 9면의(즉, 기능)그 기능에/(1-r)범위 r<>이내에 실현된 출자를 보여 준다. 그렇게me 함수는 r < 1. 범위 내의 / (1 - r) 이외의 함수를 제외하고, 특히 유용한 계수의 변경은 테일러 시리즈에 의해 정의되며, 이 시리즈는 함수의 합이 범위 내에서 충분히 매끄러운 함수로 수렴되도록 계수를 변경하는 방법을 설명한다.

공통비율 r

기하 급수 a + ar + ar² + ar³ + ar + ... 계수 a와 공통 비율 r의 두 파라미터만으로 정의되는 무한 시리즈. 공통 비율 r은 시리즈에서 전기에 대한 모든 항의 비율이다. 또는 동등하게, 공통 비율 r은 시계열에서 다음 항을 계산하는 데 사용되는 용어다. 다음 표는 몇 가지 기하학적 시리즈를 보여준다.

기하계열의 수렴은 공통비율 r:의 값에 따라 달라진다.

• r < 1일 경우, 시계열의 항이 한계에서 0에 가까워지고(크기 크기가 점점 작아지고), 시계열이 a /(1 - r) 합으로 수렴된다.
• r = 1이면 시리즈가 수렴되지 않는다. r = 1일 때 시리즈의 모든 항이 동일하고 시리즈가 무한하다. r = -1일 때 항은 두 값을 번갈아 취한다(예: 2, -2, 2, -2, 2,...). 용어의 합은 두 값 사이에서 진동한다(예: 2, 0, 2, 0, 2, ...). 이것은 다른 종류의 차이점이다. 예를 들어 그란디의 시리즈 1 - 1 + 1 + 1 + ···를 참조하십시오.
• r > 1이면 시리즈의 항은 크기가 점점 커진다. 용어들의 합도 점점 더 커지고, 시리즈는 합으로 수렴되지 않는다. (시리즈가 갈라진다.)

수렴율도 공통비율 r의 값에 따라 달라진다. 구체적으로는 r이 1이나 -1에 가까워질수록 수렴 속도가 느려진다. 예를 들어, a = 1을 갖는 기하계열은 1 + r + r²³ + r + ...이다. 그리고 r < 1일 때 1 / (1 - r)로 수렴한다. 그러나 /(1 - r)가 무한대에 접근하고 시리즈의 각 항이 1보다 작거나 같기 때문에 r이 1에 가까워짐에 따라 수렴에 필요한 항 수가 무한대에 접근한다. 이와는 대조적으로 r이 -1에 근접함에 따라 기하계열의 처음 몇 항의 합은 1/2로 수렴하기 시작하지만 가장 최근에 추가된 항이 짝수인지 홀수인지에 따라 위나 아래로 약간 뒤집힌다. r = -1 근처의 플립 동작은 a = 1과 r < 1을 가진 기하학적 시리즈의 처음 11개 항을 보여주는 인접한 이미지에 설명되어 있다.

공통 비율 r과 계수 a도 기하 급수를 정의하는데, 기하 급수는 기하 급수 단어의 목록이지만 추가는 없다. 따라서 기하 급수 a + ar + ar² + ar³ + ar + ... 기하학적 진행(기하학적 시퀀스라고도 함) a, ar, ar², ar³, ar, ... 기하학적 진행은 - 간단하지만 - 놀라운 수의 자연 현상을 모델링한다.

• 허블의 상수에 의해 정의되는 공통 비율 r이 우주의 팽창과 같은 가장 큰 관측들 중에서,
• 방사성 탄소-14 원자의 붕괴와 같은 일부 최소 관측치에 대해, 공통 비율 r은 탄소-14의 반감기로 정의된다.

또한, 공통 비율 r은 r e와^iθ 같은 복잡한 숫자가 될 수 있다. 여기서 r은 벡터의 크기(또는 길이)이고, complex은 복잡한 평면에서 벡터의 각도(또는 방향)이며² i = -1이다. 공통 비율 r e와^iθ 함께 기하학 계열의 확장된 형태는 + r e^iθ + r^i2θ e + r^i3θ e + ...이다. θ 선형적으로 시간 각 주파수ω0(다른 말로 하면, 그 대체 θ)ω0t를 만들고)의 비율은 기하학적 시리즈가 되+는 reiω0t+는 r2ei2ω0t+는 r3ei3ω0t+..., 길이의 첫 임기는 벡터가 전혀, 그리고 회전하는 전부가 아니고 다른 조건은 벡터 확장된 형태로 증가한 각도 모델.다른 lengths 기본 각도 주파수 Ω의₀ 고조파에서 회전한다. 제약 조건 r <1은 서로 다른 길이의 이 무한한 수의 벡터들을 서로 다른 속도로 회전시켜 인접한 비디오에 보이는 것처럼 원을 추적하는 것으로 조정하기에 충분하다. 테일러 시리즈가 계수를 변경하여 시리즈가 범위 내에서 충분히 매끄러운 기능을 선택한 사용자로 수렴되도록 하는 방법과 유사하게, 푸리에 시리즈는 계수를 변경하는 방법(벡터의 초기 각도를 지정하기 위해 복잡한 숫자도 될 수 있음)을 설명하여 시리즈가 사용자 선택자에게 수렴되도록 한다.d 주기 함수

합계

폐쇄형식식

$r{\displaystyle }$ ${\displaystyle \ne }$ ${\displaystyle 1}$ ${\displaystyle r\neq$ 1$}$의 경우$,$ r 용어까지 포함한 기하학적 시리즈의 첫 번째 n+1 항의 합계는 다음과 같다.

${\displaystyle a+ar+ar^{2}+ar^{3}+\cdots +/cdots +ar^{n}=\sum _{k=0}^{n}ar^{k}=a\refrac{1-r^{1-r}}}{1-r}}\right),}$

여기서 r은 공통 비율이다. 다음과 같은 많은 자기 유사어를 빼면 부분 합계 s에 대한 폐쇄형 공식(closed-form 공식)을 도출할 수 있다.^[2][3][4]

${\displaystyle {\begin{aligned}s=a\ +\ &ar\ +\ ar^{2}\ +\ ar^{3}\ +\ \cdots \ +\ ar^{n},\\rs=\ &ar\ +\ ar^{2}\ +\ ar^{3}\ +\ \cdots \ +\ ar^{n}\ +\ ar^{n+1},\\s-rs=\ &a\ -\ ar^{n+1},\\s(1-r)=\ &a(1-r^{n+1}),\\s=\ &a\left({\frac {1-r^{n+1}}{1-r}}\right)\quad {\text{(if }}r\neq 1{\text{)}}}.\end{aigned}}$

n이 무한대에 접근함에 따라 r의 절대값은 시리즈가 수렴하기 위해서는 1보다 작아야 한다. 그러면 합계가 된다.

${\displaystyle a+ar+ar^{2}+ar^{3}+ar^{4}+\cdots=\sum _{k=0}^{\inflit }={\frac {a}{1-r},{\text{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

a = 1인 경우, 이 값은 다음과 같이 단순화할 수 있다.

${\displaystyle 1\,+\,r\,r^{2}\,+\,r^{3}\,+\cdots \;=\;{\frac {1}{1-r}}.}$

이 공식은 또한 복합 r을 포함하며, 그에 상응하는 제약이 있는 r의 계수는 절대적으로 1보다 작다.

한편, 무한 시리즈가 수렴되는가에 대한 질문은 근본적으로 두 값 사이의 거리에 대한 질문이다: 충분한 조건을 주어진다면, 부분 합이 임의로 그것이 접근하고 있는 값에 가까워지는가? 기하 계열의 닫힌 형태의 위 파생에서, 두 값 사이의 거리에 대한 해석은 숫자 라인에서 그들의 위치 사이의 거리 이다. 그것은 두 값 사이의 거리에 대한 가장 일반적인 해석이다. 그러나 현대 수 이론에서 결정적인 개념이 된 p-adic 메트릭스는 기하 급수 1 + 2 + 4 + 8 + ...와 같은 거리에 대한 정의를 제공한다. a = 1과 r = 2를 사용하면 실제로 r이 일반적인 수렴 범위 r < 1을 벗어나더라도 / (1 - r) = 1 / (1 - 2) = -1로 수렴한다.

정합성 증명

우리는 기하학적 연속성이 기하학적 진행을 위한 합 공식을 사용하여 수렴된다는 것을 증명할 수 있다.

${\displaystyle {\r^{r^{2}+r^{3}+{2}+r^{3}+\cdots \ &=\lim _{n\n\\n\\n\\n\\\n\\\n\\\\n\\\n\\n\\n\n\ft\ft\ftft}/ftft}\\&=\lim _{n\rightarrow \inflt }{{1-r^{n+1}{1-r}}.\end{정렬}}}$

번째 동일성은 r< ,${\displaystyle$ r $<1,}$이면 $r{\displaystyle {}^{}}$ $n{\displaystyle }$${\displaystyle {}^{}}$+ ${\displaystyle 1{}^{}}$→ 0 $[\displaystyle$ r$^{n+1}\to$ $\$fty $},$ 그리고$$ r</$displaystyle n\to$ \$infty }$으로 0}이$($가)이${\displaystyle (}$가) 되기 때문에 참이다.

${\displaystyle {\r^{2}(+r+r^{2}+\cdots +r^{n})(1-r)&=(1-r)+(r-r^{2})+(r^{2}-r^{3})+(r^{3})+(r^{3})++++++(r^{r^}+)+)+)+)++++++++++++++++++(r^{n}-r^{n+1})\\&=(1+(-r+r)+(-r^{2}+r^{2})++++++...+(-r^{n}+r^{n})-r^{n+1}\\&=1-r^{n+1}.\end{정렬}}}$

기하 급수적인 연속물의 수렴은 같은 텔레스코핑 시리즈로 시리즈를 다시 쓰는 것으로도 증명할 수 있다. 함수를 고려하십시오.

${\displaystyle g(K)={\frac {r^{K}{1-r}}.}$

참고:

${\displaystyle 1=g(0)-g(1),\message r=g(1)-g(2),\message r^{2}=g(2)-g(3),\ldots }$

그러므로,

${\displaystyle S=1+r+r^{2}+r^{3}+\cdots =(g(0)-g(1)+(g(1)-g(2)+(g(2)+(-g(3)+)+\cdots .}$

만약

${\displaystyle r <1}$

그때

${\displaystyle g(K)\longrightarrow 0{\text{{}} }K\to \infit .}$

그래서 S는 로 수렴한다.

${\displaystyle g(0)={\frac {1}{1-r}}.}$

수렴율

위의 증명에서 보듯이, r의 n번째 힘까지 포함한 기하계열 부분합계의 폐쇄형태는 r의ⁿ⁺¹ 모든 값에 대해 a(1 - r) /(1 - r)이며, 기하계열의 폐쇄형태는 r < 1의 범위 내에 있는 전체합 a /(1 - r)이다.

공통 비율이 0 < r < 1> 범위 내에 있는 경우, 추가된 각 항에 따라 부분 합계 a(1ⁿ⁺¹ - r) / (1 - r)가 증가하여 결과적으로 작은 오차, E, 전체 합계 a / ( 1 - r)의 비율이 된다. 오류 임계값에서 n을 해결하는 중,

${\displaystyle {\begin{aligned}a\left({\frac {1-r^{n+1}}{1-r}}\right)&\geq a\left({\frac {1-E}{1-r}}\right),\\1-r^{n+1}&\geq 1-E,\\r^{n+1}&\leq E,\\\ln(r^{n+1})&\leq \ln(E),\\(n+1)\ln(r)&\leq \ln(E),\\n+1&\geq \left\lceil {\frac {\ln(E)}{\ln(r)}}\right\rceil ,\end{aligned}}}$

여기서 0 < r < 1, 천장 작동 $\lceil {\displaystyle }$ {\$displaystyle \lceil \rceil }}$은 정수로 n을 구속하고$$, 양면을 rr의 자연 로그로 나눈 것은 음수이기 때문에 불평등을 뒤집는다. 결과 n+1은 전체 합계 a / (1 - r)의 aE / (1 - r) 내에서 얻는 데 필요한 부분 합계 항의 수입니다. 예를 들어, r=0.1에서 전체 합 a /(1 - r)의 1% 이내를 얻으려면 부분 합계의 2개(=ln(E)/ln(r) = ln(0.01)/ln(0.1) 조건만 있으면 된다. 단, r=0.9에서 부분 합계의 44(= ln(0.01) / ln(0.9)항은 전체 합 a /(1 - r)의 1% 이내를 얻기 위해 필요하다.

공용 비율이 범위 내에서=<>r<0, 그 후 기하학적 시리즈는 교대 급수라non-alternating 등비 급수의 형태에 침입해서 그 같은 방법으로 일반적인 비율 범위에 0<>r<>1를 통합의률을 분석해 조건의 쌍 결합시켜 변환될 수 있다.특히 이 제3부 분합

s = a + ar + ar² + ar³ + ar⁴ + ar + ar⁵ + ... + ar^n-1 + arⁿ 범위 -1 < r < 0은 다음과 같다.

s = a - ap + ap² - ap³ + ap⁴ - ap⁵ + ... + ap^n-1 - n이 홀수이고, p = -r을 대체하며, 0 < p < 1의 범위 내에 있는 apⁿ

s = (a - ap) + (ap² - ap³) + (ap⁴ - ap⁵) + (ap - ap) + … (ap^n-1 - ap) + (ap - apⁿ)가 서로 인접하고 서로 다른 서명된 용어들이 함께 쌍을 이룬 경우,

s = a(1 - p) + a(1 - p)p² + a(1 - p)p⁴ + ... + a(1 - p)p^2(n-1)/2(각 항에서 a(1 - p)를 인수하는 경우,

s = a(1 - p) + a(1 - p)p² + a(1 - p)p⁴ + … + a(1 - p)p^2m(대체 m = (n - 1) / 2인 경우, n은 홀수인 제약 조건,

계수 a(1 - p)와 공통 비율 p를² 갖는 기하 급수 시리즈의 첫 번째 m 항의 형태가 되었다. 따라서 부분 합계의 닫힌 형태는 a(1 - p)(1^2(m+1) - p) / (1² - p) / (1 - p)이며, 각 추가 기간에 따라 증가하며 결국 작은 오차 E, 전체 합 a(1 - p) / (1 - p)의² 비율 내에 도달한다. 이전과 같이, 그 오류 임계값에서 m을 해결하기 위해,

${\displaystyle{\begin{정렬}(1-p)\left({\frac{1-p^{2m+2}}{1-p^{2}}}\right)&, \geq a(1-p)\left({\frac{1-E}{1-p^{2}}}\right),\\1-p^{2m+2}&, \geq 1-E,\\p^{2m+2}&, \leq E,\\\ln(p^{2m+2})&,\leq \ln(E),\\(2m+2)\ln(p)&, \leq \ln(E),\\m+1&, \geq \left\lceil{\frac{\ln(E)}{2\ln(p)}}\right\rceil ,\\m+1&, \geq\left\lceil{\frac{\ln(E)}.{2\ln(-r)}}\right\rceil ,\end{정렬}}}$

여기서 0 < 1 또는 동등하게 -1 < r < 0, m+1 결과는 전체 합계 a(1 - p) / (1 - p) / (1² - p²) 내에서 얻는 데 필요한 부분 합계 항 쌍의 수입니다. 예를 들어 p=0.1에서 전체 합 a(1 - p) / (1 - p²)의 1% 이내 또는 동등하게 r=-0.1을 얻으려면 부분 합계의 1(= ln(E) / (2 ln(p) = ln(0.01) / (2 ln(0.1) 쌍의 항만 필요하다. 그러나 p=0.9 또는 동등하게 r=-0.9, 22(= ln(0.01) / (2 ln(0.9)) 쌍의 부분합이 전체합 a(1 - p) / (1 - p)의² 1% 이내를 얻기 위해 필요하다. r, n + 1의 양의 값과 음의 값에 대한 수렴 비율(일부 양의 r에 대한 오차 임계값에 도달하는 데 필요한 항의 수)을 비교하면 항상 m + 1(이 r의 음의 오차 임계값에 도달하는 데 필요한 항 쌍의 수)보다 두 배나 크지만 m + 1은 단일 항 대신 항 쌍을 가리킨다. 따라서 수렴 속도는 r = 0에 대해 대칭이며 /(1 - r)의 비대칭성을 감안할 때 놀랄 수 있다. 이러한 수렴 대칭 비율을 설명하는 데 도움이 되는 한 가지 관점은 부분 합계의 각 추가 항은 r = 1에서 무한 합에 유한 기여를 하는 반면, 각 추가 항은 r = -1에서 무한 기울기에 유한 기여를 한다는 것이다.

이와는 별도로, 이러한 유형의 수렴 분석은 사용자가 선택한 충분히 부드러운 함수의 근사치에 필요한 테일러 시리즈 용어의 수를 계산하거나 사용자가 선택한 정기 함수의 근사치에 필요한 푸리에 시리즈 용어의 수를 계산할 때 특히 유용하다.

역사적 통찰력

제노 오브 엘레아 (c.495 – c.430 BC)

2500년 전 그리스 수학자들은 이 곳을 걸어 다니는 데 문제가 있었다. 신체적으로 그들은 오늘날 우리처럼, 어쩌면 더 잘 걸을 수 있었다. 그러나 논리적으로 그들은 0보다 큰 무한히 긴 숫자의 목록이 무한대로 합치된다고 생각했다^[5]. 따라서 엘레아의 제노가 한 장소에서 다른 곳으로 걷기 위해서는 먼저 반을 걸어야 하고, 그 다음 남은 거리의 반을 걸어야 하며, 그 반을 걸어야 한다는 점을 지적한 것은 역설적인 일이었고, 그 반을 걸어야 하기 때문에 나머지 반을 무한정 많이 걸어야 한다는 것이었다.남은 거리가 얼마나 작든, 당신은 여전히 그것의 전반부를 걸어야 한다. 이리하여 엘레아의 제노는 짧은 거리를 무한히 긴 반감된 남은 거리의 목록으로 변형시켰는데, 모두 0보다 크다. 그리고 그것이 문제였습니다: 어떻게 거리가 직접 측정했을 때 짧을 수 있고, 또한 반감된 잔여물의 무한 목록을 종합했을 때 무한할 수 있는가? 그 역설은 0보다 훨씬 큰 무한히 긴 수의 목록이 무한대로 합친다는 가정에 뭔가 잘못된 것이 있음을 드러냈다.

알렉산드리아의 유클리드 (기원전 300년)

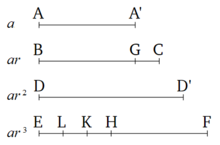
유클리드 기하학책^[6] IX, 발의안 35, 증거(인접 다이어그램 캡션의 명제:

AA, BC, DD, EF는 AA의 최소치에서 시작하여 연속적으로 비례하는 숫자의 어떤 것이든 될 수 있도록 하라. 그리고 각각 AA'와 같은 BG와 FH를 BC와 EF에서 빼도록 했다. 나는 GC가 AA에게 있기 때문에 EH는 AA, BC, DD에게 있다고 말한다.

FK를 BC와 동일하게, 그리고 FL to DD'로 만드세요. 그리고 FK는 BC와 같기 때문에, 그 중 FH는 BG와 같기 때문에, 나머지 HK는 나머지 GC와 같다. 그리고 EF가 DD'에 속하므로 DD는 BC로, BC는 AA에 [제안 7.13호]로, DD는 FL로, BC는 FK로, AA는 FH로 같기 때문에 EF는 FL로, FF는 FK로, FK는 FH로 같다. 분리하여 EL에서 LF로, 따라서 LK에서 FK로, KH에서 FH로 [제안 7.11호, 7.13호] 따라서 선행의 하나로서 다음 중 하나에 해당하므로 (합계) 선행의 모든 합계는 (합계) 다음의 모든 것을 (합계)한다 [제안 7.12]. 그러므로 KH가 FH에 있듯이 EL, LK, KH to LF, FK, HF. 그리고 KH는 CG, FH는 AA, LF, FK, HF는 DD, BC, AA'와 같다. 그러므로, CG가 AA에게 있듯이, EH to DD, BC, AA'에 해당된다. 그러므로 초의 초과가 초의 초과인 것처럼, 마지막의 초과도 그 이전의 모든 사람에게 해당된다. 보여줘야 할 바로 그 모습.

유클리드 의 명제와 증거의 엄격함은 필수가 되었을지도 모른다. 있는 그대로, 기하학의 원소는 500페이지가 넘는 명제와 증거들이다. 이 인기 있는 교과서를 복사하는 것은 1440년이 되어서야 인쇄기가 발명되었다는 점에서 노동 집약적이었다. 그리고 이 책의 인기는 오랫동안 지속되었다: 인용된 영어 번역본 "기하의 요소들"에서 언급된 바와 같이, "세계에서 가장 오래된 연속적으로 사용되는 수학 교과서"라는 특징이 있다. 그래서 매우 간결한 것은 매우 실용적인 것이었습니다. IX 책의 발의안 제35호에 대한 증명은 유클리드사가 시리즈에서 서로 다른 용어의 특정 선분할의 길이를 명시적으로 동일시하는 것을 어떻게든 피할 수 있었다면 훨씬 더 압축적일 수 있었을 것이다. 예를 들어, 기하 계열의 현대 표기법(예: + ar + ar² + ar³ + ar + ar + ...) + arⁿ)는 서로 동일한 항의 특정 부분에 라벨을 표시하지 않는다.

또한 인용된 소개에서 편집자의 논평은

원소에 등장하는 대부분의 이론은 유클리드 자신이 발견한 것이 아니라 피타고라스(및 그의 학교), 키오스의 히포크라테스, 아테네의 테에테투스, 신이도스의 에우독소스 등 초기 그리스 수학자들의 작품이었다. 그러나 유클리드는 일반적으로 이러한 이론들을 논리적인 방법으로 배열한 것으로서, 그들이 반드시 다섯 가지의 단순한 공리에서 따르는 것을 (적용하여 현대 수학이 요구하는 엄격함으로 항상 그렇지는 않다) 증명한다. 유클리드 또한 이전에 발견된 이론에 대한 많은 특히 기발한 증거를 고안한 것으로 인정받고 있다(예: 제1권 정리 48).

명제와 증거를 현재의 표기법을 사용하는 형태로 번역하는 것을 돕기 위해, 도표에는 몇 가지 수정 사항이 있다. 첫째로, 기하 급수적인 시리즈의 처음 4개 항의 값을 나타내는 4개의 수평선 길이는 이제 다이어그램의 왼쪽 여백에 a, ar, ar², ar³, ar로 표시되어 있다. 둘째, 새로운 라벨 A'와 D'가 이제 첫 번째와 세 번째 라인에 있으므로 다이어그램의 모든 라인 세그먼트 이름이 세그먼트의 시작점과 끝점을 일관되게 지정한다.

제안의 구문 해석은 다음과 같다.

이와 유사하게, 다음은 증명에 대한 문장 해석에 의한 문장이다.

시라큐스의 아르키메데스(C.287 – BC.212)

아르키메데스는 포물선과 직선으로 둘러싸인 영역을 계산하기 위해 기하 급수적인 시리즈의 합계를 사용했다. 그의 방법은 그 지역을 무한한 수의 삼각형으로 해부하는 것이었다.

아르키메데스의 정리에는 포물선 아래의 총 면적이 청색 삼각형 면적의 4/3이라고 되어 있다.

아르키메데스는 각 녹색 삼각형의 면적이 파란색 삼각형의 1/8이고, 각각의 노란색 삼각형의 면적이 녹색 삼각형의 면적이 1/8이라고 결정했다.

파란색 삼각형에 영역 1이 있다고 가정할 때 전체 면적은 무한 합이다.

${\displaystyle 1\,+\,2\frac\{1}{8}\{1}\frac\frac {1}{8}\,+\,+\,+\,+\,+\{8}}}^{3}\,+\,\cdots .}$

제1항은 푸른 삼각형의 영역을 나타내고, 제2항은 두 개의 녹색 삼각형의 영역을 나타내며, 제3항은 네 개의 노란 삼각형의 영역 등을 나타낸다. 분수를 단순화하는 것은

${\displaystyle 1\,+\,{\frac {1}{4}\,+\,{\frac {1}{16}\,+\,{\frac {1}{64}\,+\,\cdots .}}$

이것은 공통비 1/4을 갖는 기하학적 직렬이고 분수 부분은 다음과 같다.

${\displaystyle \sum \sum _{n=0}^{-n}=1+4^{-1}+4^{-2}+4^{-3}+\cdots ={4 \over 3}.}$

합계는

${\displaystyle {\frac {1}{1-r}\;=\;{\frac {1}{1-{\frac {1}{4}}\=\\\frac {4}{3}}}.}$

이 계산은 통합의 초기 버전인 소모 방법을 사용한다. 미적분을 사용하면 확실한 적분으로 동일한 영역을 찾을 수 있었다.

니콜 오레스메(c.1323 – 1382)

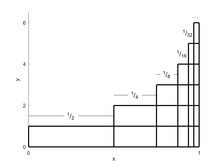
무한 시리즈에 대한 그의 통찰 중에서, 니콜 오레스미는^[7] 조화 시리즈의 분리에 대한 우아하게 간단한 증거 외에도, 시리즈 1/2 + 2/4 + 3/8 + 4/16 + 5/32 + 6/64 + 7/128 + ...을 증명했다. 2로 수렴하다. 그의 기하학적 증거에 대한 도표는 인접한 도표와 유사하게 2차원 기하학적 시리즈를 보여준다. The first dimension is horizontal, in the bottom row showing the geometric series S = 1/2 + 1/4 + 1/8 + 1/16 + ... , which is the geometric series with coefficient a = 1/2 and common ratio r = 1/2 that converges to S = a / (1-r) = (1/2) / (1-1/2) = 1. The second dimension is vertical, where the bottom row is a new coefficient a_T equal to S and each subsequent row above it is scaled by the same common ratio r = 1/2, making another geometric series T = 1 + 1/2 + 1/4 + 1/8 + ... , which is the geometric series with coefficient a_T = S = 1 and common ratio r = 1/2 that converges to T = a_T / (1-r) = S / (1-r) = a / (1-r) / (1-r) = (1/2) / (1-1/2) / (1-1/2) = 2.

3차원을 넘어서 시각화하기는 어렵지만, 오레스메의 통찰력은 어떤 차원 d에도 일반화된다. 기하 급수 d-1 치수의 합계를 기하 급수 a의 계수로 사용하면 d차원 기하 급수가 r <1> 범위 내에서 S / a = 1 / (1-r)^d로^d 수렴된다. 파스칼의 삼각형과 긴 분할은 이러한 다차원 기하학적 계열의 계수를 드러내는데, 여기서 닫힌 형태는 r <1> 범위 내에서만 유효하다.

${\displaystyle {\begin{matrix}{\text{ 1}}\\{\text{ 1}}\quad {\text{ 1}}\\{\text{ 1}}\quad {\text{ 2}}\quad {\text{ 1}}\\{\text{ 1}}\quad {\text{ 3}}\quad {\text{ 3}}\quad {\text{ 1}}\\{\text{ 1}}\quad {\text{ 4}}\quad {\text{ 6}}\quad {\text{ 4}}\quad {\text{ 1}}\end{matrix}}}$

${\displaystyle {\begin}&d\quad S^{d}/a\\\\text{d}/a\(확장 양식)}}\\&1\quad 1/(1-r)\quad &&1+r+r^{2}+r^{3}+r^{4}+\cdots \\&2\quad 1/(1-r)^{2}\quad &&1+2r+3r^{2}+4r^{3}+5r^{4}+\cdots \\&3\quad 1/(1-r)^{3}\quad &&1+3r+6r^{2}+10r^{3}+15r^{4}+\cdots \\&4\quad 1/(1-r)^{4}\quad &&1+4r+10r^{2}+20r^{3}+35r^{4}+\cdots \\\end{aligned}}}$

긴 분할의 대안으로 d-1 치수의 계수를 통합하여 d-차원 기하계열의 계수를 계산하는 것도 가능하다는 점에 유의한다. 파워 시리즈 합계 도메인의 1-r 분할에서 파워 시리즈 계수 도메인의 통합에 이르는 이 매핑은 라플라스 변환에 의해 수행되는 개별적인 형태의 매핑이다. MIT의 아서 마턱 교수는 이 강의 비디오에서 라플라스 변환을 파워 시리즈에서 어떻게 도출하는지를 보여준다.^[8] 여기서 파워 시리즈는 이산 계수와 합금 사이의 매핑이고 라플라스 변환은 연속 가중치와 적분 사이의 매핑이다.

폐쇄형^d S/a는 S = f(r) = 1 / (1-r)의 파생상품과 관련이 있지만 동일하지는 않다. 다음 표에서 보듯이 관계는^k+1 S = f^(k)(r) / k!이며, 여기서^(k) f(r)는 f(r) = 1 / (1-r)의^th k 파생상품을 나타내며 닫힌 형태는 r < 1 범위 내에서만 유효하다.

${\displaystyle {\displaystyle}&k\f^{(k)}(r)/a\\text{(closed form)}\display &&f^{(k)/a\text{(closure form)}}\\&, 0\quad 1(1-r)\quad&&\sum _{j=0}^{\infty}r^{j}\\&, 1\quad 1!(1-r)^{2}\quad&&\sum _{j=1}^{\infty}jr^{j-1}\\&, 2\quad 2!(1-r)^{3}\quad&&\sum _ᆸ^ᆹj(j-1)r^{j-2}\\&, 3\quad 3!(1-r)^{4}\quad&&\sum _ᆼ^ᆽj(j-1)(j-2)r^{j-3}\\&, 4\quad 4!(1-r)^{5}\quad&&\sum _{j=4}^{\i.nfty}j(j-1)(j-2)(j-3)r^{j-4}\\\end{정렬}}}$

적용들

반복 소수점

반복적인 십진법은 공통비율이 1/10인 기하계열이라고 생각할 수 있다. 예를 들면 다음과 같다.

${\displaystyle 0.777\ldots \;=\{\frac {7}{10}\,+\,{\frac {7}{100}\,+\,{\frac}{7}{1000}\,+\,{\frac}{10000},+\cdots.}$

기하 계열의 합계에 대한 공식은 십진수를 분수로 변환하는데 사용될 수 있다.

${\displaystyle 0.777\ldots \;=\;{\frac {a}{1-r}\;=\;{\frac {7/10}{1-1/10}\;;;;;;;;;;;{\frac {7/10}{1/10};;;;;;;;;;;;=\;{\frac {7/10}{9/10}\;=\;{\frac {7}{9}.}$

이 공식은 단일 반복 수치뿐만 아니라 반복적인 수치 그룹에도 적용된다. 예를 들면 다음과 같다.

${\displaystyle 0.12341234\ldots \;=\;{\frac {a}{1-r}\;=\;{\frac {1234/10000}{1-1/10000}\;;;;;;;;;;;;;&frac {1234/10000}{1-1;;;;;;;;;;;;;;;;;=\;{\frac {1234/10000}{99999/10000}\;=\;{\frac {1234}{9999}}.}$

각 연속 소수점 연속은 다음과 같이 편리하게 단순화할 수 있다는 점에 유의하십시오.

${\displaystyle 0.090909\ldots \;=\;{\frac {09}{99}\;=\;{\frac {1}{11}}.}$

${\displaystyle 0.14381438\ldots \;=\;{\frac {1438}{9999}.}$

${\displaystyle 0.9999\ldots \;=\;{\frac {9}{9}\;=\;1.}$

즉, 반복 길이가 n인 반복 십진법은 반복 부분(정수로서)의 몫과ⁿ 10 - 1과 같다.

경제학

경제학에서 기하계열은 연금(정기적으로 지급되는 돈의 합계)의 현재가치를 나타내기 위해 사용된다.

예를 들어, 연금의 소유주에게 매년 1회(연말) 100달러를 영구적으로 지급한다고 가정해 보자. 지금부터 1년에 100달러를 받는 것은 당장 100달러도 안 되는 가치가 있는데, 그 돈을 받기 전에는 투자할 수 없기 때문이다. 특히 향후 연간 100달러의 현재가치는 100달러 / (1 + $I{\displaystyle }$ ${\displaystyle I}$ )이며,$$ 여기서 $I{\displaystyle }$ ${\displaystyle I}$은 연이자율이다.

마찬가지로 향후 2년간 100달러의 지급액은 현재가치가 $100 / ($1{\displaystyle }$ + I ${\displaystyle I}$²) (지금 당장 돈을 받지 않음으로써 2년치의 이자를 잃기 때문에 제곱)이다. 따라서 매년 100달러를 영속적으로 수령하는 현재의 가치는 다음과 같다.

${\displaystyle \sum _{n=1}^{\inflt }{\frac {\$100}{(1+I)^{n}}}}$

무한 시리즈:

${\displaystyle {\frac {\$100}{\$100}}}}\,+\,{\frac {\$100}{1+I)^{2}}}\,+\,{\frac {\$100}{(1+I)^{3}}}\,+\,{\frac {\$100}{(1+I)^{4}}}\,+\,\cdots .}$

이것은 공통 비율 1 / ($1{\displaystyle }$ + I ${\displaystyle I}$ )$$의 기하학적 시리즈 입니다. 합계는 첫 번째 항을 (1 - 공통 비율)로 나눈 값이다.

${\displaystyle {\frac {\$100/(1+I)}{1-1/(1+I)}\;=\;{\frac {\$100}{I}}}$

예를 들어, 연간 이자율이 10%(${\displaystyle }$ ${\displaystyle$I} = 0.10)이면 전체 연금액은 현재가치가 100달러 / 0.10달러 = 1000달러인 것이다.

이러한 종류의 계산은 대출금의 APR(예: 주택담보대출)을 계산하는 데 사용된다. 또한 기대주 배당금의 현재가치 또는 유가증권의 말단가치를 추정하는 데도 사용할 수 있다.

프랙탈 기하학

프랙탈의 연구에서 기하학적 직렬은 종종 자기 유사 도형의 둘레, 면적 또는 부피로서 발생한다.

예를 들어, 코흐 눈송이 내부의 영역은 무한히 많은 정삼각형의 결합이라고 설명할 수 있다(그림 참조). 녹색 삼각형의 각 면은 큰 파란색 삼각형의 면의 1/3 크기여서 면적이 1/9이다. 마찬가지로, 각각의 노란 삼각형은 녹색 삼각형의 면적의 1/9을 가지고 있다. 푸른 삼각형을 면적의 단위로 보아 눈송이의 전체 면적은

${\displaystyle 1\,+\,3\frac\1}{9}\{1}{9}\,+\,12\frac\{1}{9}\,+\,48\frac\{1}{1}{9}\\cdots .}$

이 시리즈의 첫 번째 항은 청색 삼각형의 면적, 두 번째 항은 녹색 삼각형의 총 면적, 세 번째 항은 12개의 황색 삼각형의 총 면적 등을 나타낸다. 초기 1을 제외하고, 이 시리즈는 일정한 비율 r = 4/9로 기하학적이다. 기하계열의 첫 번째 항은 a = 3(1/9) = 1/3이므로 합은

${\displaystyle 1\,+\,{\frac {a}{1-r}\;=\1\,+\,{\frac {1}{3}{1-{\frac}{4}}}}}\\\\\frac {8}{5}}.}$

따라서 코흐 눈송이는 기저 삼각형의 면적의 8/5를 가진다.

기하급수적 동력계

기하 급수식

${\displaystyle {\frac {1}{1-x}=1+x+x^{2}+x^{3}+x^{4}+\cdots }$

의 정리 감각에서는 파워 시리즈로 해석할 수 있는데, x< $>$ <\$디스플레이$ 스타일 $x <1}.$ 이로부터 다른 파워 시리즈를 얻기 위해 추론할 수 있다 예를 들어,

${\displaystyle {\regated}\tan^{-1}(x)&=\int {\frac {dx}{1+x^{2}}}\\&=\int {\frac {dx}{1-(-x^{2})}}\\&=\int \left(1+\left(-x^{2}\right)+\left(-x^{2}\right)^{2}+\left(-x^{2}\right)^{3}+\cdots \right)dx\\&=\int \left(1-x^{2}+x^{4}-x^{6}+\cdots \right)dx\\&=x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-{\frac {x^{7}}{7}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1}.\end{정렬}}}$

참고 항목

• 0.999... – 숫자 1의 대체 소수점 확장
• 점근법 – 무한대 경향이 있는 지점에서 접선 선의 한계
• 다이버전트 기하 급수
• 일반화된 초기하 함수
• 기하급수
• 노이만계 전동차
• 비율 검정
• 루트 테스트
• 시리즈(수학) – 무한대 합계
• 산술계열

특정 기하 급수

• 그란디의 시리즈 – 1항과 -1항 교대의 무한 합: 1 - 1 + 1 - 1 + 1 + 1 + ⋯
• 1 + 2 + 4 + 8 + ⋯ – 무한 시리즈
• 1 − 2 + 4 − 8 + ⋯
• 1/2 + 1/4 + 1/8 + 1/16 + ⋯
• 1/2 − 1/4 + 1/8 − 1/16 + ⋯
• 1/4 + 1/16 + 1/64 + 1/256 + ⋯
• 기하계열은 r < 1과 + r = 1인 경우에만 단위계열(시리즈 합이 1로 수렴됨)이다(r < 1인 경우 보다 친숙한 형태 S = a / (1 - r) = 1인 경우와 동일함). 따라서 교대계열은 -1 < r < 0>과 a + r = 1일 때(예: 계수 a = 1.7, 공통 비율 r = -0.7)의 단위계열이기도 하다.
• 기하계열의 항은 또한 일반화된 피보나치 수열의 항(F_n = F_n-1 + F_n-2, 그러나 F₀ = 0 및 F₁ = 1)이 기하계열 공통비율 r이 제약조건 1 + r = r을² 만족하는 경우, 2차 공식에 따르면 공통비율 r이 황금비율(즉, 공통비율 r = (1 ± √5)/2)과 같은 경우다.
• 단위 시리즈로 일반화된 피보나치 수열의 항을 가진 유일한 기하계열은 계수 a로서 황금비율을, 결합금비는 공통비 r(즉 a = (1 + +5)/2와 r = (1 - 55)/2)로 한다. + r = 1과 r < 1이기 때문에 단위계열이고, 1 + r = r이기² 때문에 일반화된 피보나치계열이고, r < 0이기 때문에 교대계열이다.

메모들

참조

외부 링크

• "Geometric progression", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Weisstein, Eric W. "Geometric Series". MathWorld.
• PlanetMath의 기하 시리즈.
• Peppard, Kim. "College Algebra Tutorial on Geometric Sequences and Series". West Texas A&M University.
• Casselman, Bill. "A Geometric Interpretation of the Geometric Series". Archived from the original (Applet) on 2007-09-29.
• 2007년 Wolfram 데모 프로젝트, Michael Schreiber의 "Geometric Series"