발산

벡터 미적분학에서 발산(diversity)은 벡터장(vector field)에서 작용하는 벡터 연산자로, 각 지점에서 벡터장(vector field)의 선원의 수량을 주는 스칼라장을 생성한다.좀 더 기술적으로, 이 차이는 주어진 점 주위의 최소 부피에서 벡터장 외속의 부피 밀도를 나타낸다.

예를 들어, 공기가 가열되거나 식을 때 공기를 고려하십시오.각 지점에서 공기의 속도는 벡터장을 정의한다.어떤 지역에서 공기가 가열되는 동안, 그것은 모든 방향으로 팽창하고, 따라서 속도장은 그 지역에서 바깥쪽으로 향한다.따라서 그 지역에서 속도장의 차이는 양의 값을 가질 것이다.공기가 냉각되어 수축하는 동안, 속도의 차이는 음의 값을 가진다.

다양성의 물리적 해석

물리적인 측면에서 벡터장의 발산이란 벡터장 플럭스가 주어진 지점에서 소스처럼 작용하는 범위를 말한다.그것은 그것의 "outgoing"의 국지적인 척도로, 즉 극소수의 공간에 들어가는 것보다 더 많은 수의 필드 벡터가 나오는 범위다.플럭스가 나가는 지점은 양의 발산성을 가지며, 흔히 필드의 "출처"라고 불린다.유속이 안쪽으로 향하는 지점은 음의 분산을 가지며, 흔히 밭의 "싱크"라고 불린다.주어진 점을 둘러싸고 있는 작은 표면을 통과하는 장의 유동성이 클수록 그 지점에서의 발산 값도 커진다.둘러싸인 표면을 통해 유속이 0인 지점은 0의 차이를 가진다.

벡터장의 분비는 액체나 기체의 속도장의 예를 사용하여 종종 설명된다.움직이는 기체는 각 지점에서 벡터로 나타낼 수 있는 속도, 속도, 방향을 가지고 있으므로 기체의 속도는 벡터장을 형성한다.가스가 가열되면 팽창한다.이것은 모든 방향에서 바깥쪽으로 가스 입자의 순운동을 일으킬 것이다.가스의 어떤 닫힌 표면은 팽창하고 있는 가스를 둘러싸게 될 것이고, 따라서 가스의 바깥쪽 유속이 표면을 통과하게 될 것이다.그래서 속도계는 어디에서나 긍정적인 차이를 보일 것이다.마찬가지로 기체가 냉각되면 수축한다.어떤 부피에서든 가스 입자를 위한 공간이 더 많아질 것이기 때문에 유체의 외부 압력은 어떤 밀폐된 표면을 통해 안으로 가스 부피의 순흐름을 유발할 것이다.그러므로 속도장은 어디에나 음의 분열을 가지고 있다.이와는 대조적으로 일정한 온도와 압력의 기체에서는 어떤 닫힌 표면에서 나오는 기체의 순유속이 0이다.기체는 움직이고 있을지 모르지만, 어떤 밀폐된 표면으로 흘러들어오는 기체의 부피율은 흘러나오는 부피율과 같아야 하므로 순유속은 0이다.따라서 기체 속도는 모든 곳에서 0의 차이를 가진다.모든 곳에 0의 분기가 있는 분야를 솔레노이드라고 한다.

기체가 한 지점이나 작은 지역에서만 가열되거나, 한 지점에서 추가 기체의 공급원을 공급하는 작은 튜브가 도입되면, 그곳의 기체는 팽창하여 주변의 유체 입자를 사방으로 바깥쪽으로 밀어낼 것이다.이것은 가열된 지점을 중심으로 가스 전체에 외향 속도장을 발생시킬 것이다.가열된 지점을 감싸고 있는 닫힌 표면은 기체 입자가 그 밖으로 흘러 나오는 유동성을 가질 것이기 때문에, 그 지점에는 양의 차이가 있다.그러나 그 점을 감싸지 않은 닫힌 표면은 내부에 일정한 기체 밀도를 가지고 있기 때문에 부피에서 나오는 것처럼 많은 유체 입자가 유입되는 것과 마찬가지로 부피 밖으로 나오는 순유속은 0이다.따라서 다른 지점에서의 차이는 0이다.

정의

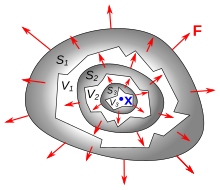
지점 x에서₀ 벡터 필드 F(x)의 차이는 V가 0으로 줄어들기 때문에 닫힌 볼륨 V를 둘러싸는 V의 볼륨에 대한₀ 닫힌 볼륨 V의 표면에서 F의 표면 적분 비율의 한계로 정의된다.

$왼쪽.\operatorname {div} \mathbf {F} \right _{\mathbf {x_{0}} }=\lim _{V\to 0}{\frac {1}{V}}}}}}}$ ${\displaystyle \scriptstyle S(V)}$ ${\displaystyle \mathbf {F} \cdot \mathbf {\hat {n}} \dS}$

여기서 V는 V의 부피, S(V)는 V의 경계, n ${\displaystyle \stackrel{}{\mathbf{^}}}$ ${\$은(는) 해당 표면에 정상적인 바깥쪽 단위다.위의 한계는 x를₀ 포함하고 0 볼륨에 접근하는 볼륨의 모든 시퀀스에 대해 항상 동일한 값으로 수렴된다는 것을 보여줄 수 있다.결과인 div F는 x의 스칼라 함수다.

이 정의는 좌표가 없기 때문에 어떤 좌표계에서도 차이가 동일하다는 것을 보여준다.그러나 그것은 종종 다양성을 계산하는데 실질적으로 사용되지 않는다; 벡터 필드가 좌표계로 주어질 때 아래의 좌표 정의는 훨씬 사용하기 쉽다.

도처에 0의 분기가 있는 벡터장을 솔레노이드라고 하는데, 이 경우 닫힌 표면에는 그 전체에 순속이 없다.

좌표 정의

데카르트 좌표, 평행 좌표.

In three-dimensional Cartesian coordinates, the divergence of a continuously differentiable vector field ${\displaystyle \mathbf {F} =F_{x}\mathbf {i} +F_{y}\mathbf {j} +F_{z}\mathbf {k} }$ is defined as the scalar-valued function:

${\displaystyle \operatorname {div} \mathbf {F} =\nabla \cdot \mathbf {F} =\left({\frac {\partial }{\partial x}},{\frac {\partial }{\partial y}},{\frac {\partial }{\partial z}}\right)\cdot (F_{x},F_{y},F_{z}}={\frac {\partial F_{x}}{\partial x}}+{\partial y_{y}}{\partial y}+{\partial y}}{\partial F_{z}}}}.}$

좌표면에서는 표현되지만 물리적 해석에서 알 수 있듯이 회전하에서는 결과는 불변한다.N차원 공간에서 N차원 벡터장 F의 자코비안 행렬의 추적은 어떤 반전성 선형 변환에서도 불변하기 때문이다.

발산 ∇·F의 공통 표기법은 편리한 니모닉으로, 여기서 점은 ∇ 연산자의 성분을 취(델 참조)하여 F의 해당 성분에 적용하고 그 결과를 합하여 도트 제품을 연상시키는 연산을 나타낸다.연산자를 적용하는 것은 구성요소를 곱하는 것과 다르기 때문에, 이것은 표기법 남용으로 간주된다.

원통좌표

로컬 단위 원통형 좌표로 표현된 벡터의 경우

${\displaystyle \mathbf {F} =\mathbf {e} _{r_{r}+\mathbf {e} _{\theta }F_{\theta }+\mathbf {e} _{z}}}$

여기서 e는_a a 방향의 단위 벡터로서, 그 차이는^[1]

${\displaystyle \operatorname {div} \mathbf {F} =\nabla \cdot \mathbf {F} ={\frac {1}{r}}{\frac {\partial }{\partial r}}\left(rF_{r}\right)+{\frac {1}{r}}{\frac {\partial F_{\theta }}{\partial \theta }}+{\frac {\partial F_{z}}{\partial z}}.}$

로컬 좌표 사용은 표현의 유효성을 위해 필수적이다.If we consider x the position vector and the functions r(x), θ(x), and z(x), which assign the corresponding global cylindrical coordinate to a vector, in general ${\displaystyle r(\mathbf {F} (\mathbf {x} ))\neq F_{r}(\mathbf {x} )}$, ${\displaystyle \theta (\mathbf$${F} (\mathbf {x} ))\neq F_{\theta }(\mathbf {x} )}$, and ${\displaystyle z(\mathbf {F} (\mathbf {x} ))\neq F_{z}(\mathbf {x} )}$. In particular, if we consider the identity function F(x) = x, we find that:

${\displaystyle \theta }$(${\displaystyle F\mathbf{}}$( x${\displaystyle }$)${\displaystyle =}$ ${\displaystyle \theta }$ ${\displaystyle \ne }$ ${\displaystyle {}_{}\theta \mathbf{}}$ ( x${\displaystyle }$)${\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle \theta (\mathbf {F} (\mathbf {x} )=\theta \neq F_{\ta }(\mathbf {x} )=0$

구형좌표

구형 좌표에서는 z축과의 각도 θ과 z축을 중심으로 회전하는 φ과 국소 단위 좌표로 다시 F를 표기하면 그 차이가 나타난다^[2].

${\displaystyle \operatorname {div} \mathbf {F} =\nabla \cdot \mathbf {F} ={\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}F_{r}\right)+{\frac {1}{r\sin \theta }}{\frac {\partial }{\partial \theta }}(\sin \theta \,F_{\theta })+{\frac {1}{r\sin \theta }}{\frac {\partial F_{\varphi }}{\partial \varphi }}.}$

텐서장

A는 다음과 같이 정의된 연속적으로 서로 다른 2차 텐서 필드가 되도록 한다.

${\displaystyle \mathbf {A} = {\begin{bmatrix}A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\\A_{31}&A_{32}&A_{33}\end{bmatrix}}}$

데카르트 좌표계의 차이점은 1차 텐서 분야로^[3] 다음 두 가지 방법으로 정의할 수 있다.^[4]

${\displaystyle \operatorname {div}(\mathbf {A} )={\cfrac {\partial A_{ik}}{\partial x_{k}}}~\mathbf {e} _{i}=}A_{ik,k}~\mathbf {e} _{i}={\begin{bmatrix}{\dfrac {\partial A_{11}}{\partial x_{1}}}+{\dfrac {\partial A_{12}}{\partial x_{2}}}+{\dfrac {\partial A_{13}}{\partial x_{3}}}\\{\dfrac {\partial A_{21}}{\partial x_{1}}}+{\dfrac {\partial A_{22}}{\partial x_{2}}}+{\dfrac {\partial A_{23}}{\partial x_{3}}}\\{\dfrac {\partial A_{31}}{\partial x_{1}}}+{\dfrac{\partial A_{32}}{\partial x_{2}}+{\dfrac {\partial A_{33}}{\partial x_{3}}}\end{bmatrix}}}}}}}}$

그리고^[5][6][7][8]

${\displaystyle \nabla \cdot \mathbf {A} ={\cfrac {\partial A_{k}}{\partial x_{k}}}}~\mathbf {e} _{i}=}A_{ki,k}~\mathbf {e} _{i}={\begin{bmatrix}{\dfrac {\partial A_{11}}{\partial x_{1}}}+{\dfrac {\partial A_{21}}{\partial x_{2}}}+{\dfrac {\partial A_{31}}{\partial x_{3}}}\\{\dfrac {\partial A_{12}}{\partial x_{1}}}+{\dfrac {\partial A_{22}}{\partial x_{2}}}+{\dfrac {\partial A_{32}}{\partial x_{3}}}\\{\dfrac {\partial A_{13}}{\partial x_{1}}}+{\dfrac{\partial A_{23}}{\partial x_{2}}+{\dfrac {\partial A_{33}}{\partial x_{3}}\end{bmatrix}}}}}}}}$

우리는 가지고 있다.

${\displaystyle \operatorname {div}(\mathbf {A^{T})=\nabla \cdot \mathbf {A}}$

만약 텐서는 대칭 Aij)아지는 그때}. 이것 때문에 ⁡(A))∇ ⋅{\displaystyle \operatorname{div}(\mathbf{A})=\nabla \cdot \mathbf{A}(및 기호 div과∇ ⋅{\displaystyle \nabla \cdot})을 교환해 어디 텐서 symm 역학 방정식(특히 사용된다 종종 문학에서 두가지 정의를 div.etry가정한다.

원통형 및 구형 좌표에서$$ ${\displaystyle A\mathbf{}}$ ${\$의 표현은 원통형 및 구형 좌표에서 기사에 제시되어 있다.

일반좌표

아인슈타인 표기법을 사용함으로써 우리는¹ 일반 좌표에서의 차이를 고려할 수 있는데ⁿ, 여기서 n은ⁱ 도메인의 치수 수입니다.여기서 상위 지수는 좌표나 성분의 수를 의미하므로 x는² 두 번째 성분을 의미하며 x 제곱 수량은 아니다.x와ⁱ 같은 임의 구성요소를 가리키는 데 사용되는 인덱스 변수 i.이 차이점은 Voss-Weyl 공식을 통해 다음과 같이 기록될 수 있다.^[9]

${\displaystyle \operatorname {div}(\mathbf {F} )={\frac {1}{\rho }}{\partial \partial \left(\rho \,F^{i}\right)}{\partial x^{i}}}}}}}}}},}}}}}}},}}}}$

여기서 $\rho {\displaystyle }$ ${\displaystyle \rho}$은(는) 볼륨 요소의 로컬 계수이고 F는ⁱ 국부적 비정상화된 공변량 기준(${\displaystyle {}_{}}$=${\displaystyle \mathrm{}}$∂ x${\displaystyle }$/${\displaystyle \mathrm{}}$∂ ${\displaystyle {}^{}}$ ${\displaystyle i^{}}$ ${\$ /$partial$ x$^{i$아인슈타인 표기법은 상위와 하위 지수로 나타나기 때문에 i에 대한 합계를 의미한다.

체적 계수 ρ은 좌표계에 따라 달라지는 위치 함수다.데카르트 좌표, 원통형 좌표, 구면 좌표에서는 전과 동일한 규약을 사용하여 각각 ρ = 1, ρ = r, = = r sin² θ을 가진다.볼륨은 $\sqrt{{\mathrm{also}}_{}}$= $\sqrt{det}$ $\sqrt{{}_{}}$ $\sqrt{a_{}}$ b $textstyle \rho ={\sqrt {\\좌측 \det g_{ab}\right$}}}(으)로 표현될 수 있으며$,$ 여기서_ab g는 메트릭 텐서(metric tensor)이다.결정 인자는 벡터 세트가 주어진 볼륨의 적절한 불변성 정의를 제공하기 때문에 나타난다.결정요소는 지수에 의존하지 않는 스칼라 수량이기 때문에 $\rho$= $\sqrt{\det }$ g $textstyle \rho ={\sqrt{\\\det$ g$\right}}}$라고 적으면서 억제할 수 있다$.$절대값은 사이비-리만 공간과 같이 결정 요인이 음수일 수 있는 일반적인 경우를 처리하기 위해 취한다.제곱근의 이유는 약간 미묘하다. 곡선에서 데카르트 좌표로 갔다가 다시 돌아오면서 효과적으로 이중 계수를 피한다.The volume (the determinant) can also be understood as the Jacobian of the transformation from Cartesian to curvilinear coordinates, which for n = 3 gives ${\textstyle \rho =\left {\frac {\partial (x,y,z)}{\partial (x^{1},x^{2},x^{3})}}\right }$.

일부 규약에서는 이전 절에서와 같이 모든 지역 기반 요소가 단위 길이로 정규화될 것으로 예상한다.표준화된 기준으로$$ ${\displaystyle e_{}}$ i ${\$을(를) 쓰고 F의 성분에 대해$$ $F{\displaystyle {\stackrel{}{}}^{}}$^ ${\displaystyle i^{}}${\$displaystyle${\$f}^{i}$을(를) 쓰면 다음과 같은 결과가 나온다.

${\displaystyle \mathbf {F} =F^{i}\mathbf {e} _{i}=F^{i}\ {\mathbf {e} _{i}}\ {\frac {\mathbf {e} _{i}}{\ \mathbf {e} _{i}\ }}=F^{i}{\sqrt {g_{ii}}}\,{\hat {\mathbf {e} }}_{i}={\hat {F}}^{i}{\hat {\mathbf {e} }}_{i},}$

메트릭 텐서의 속성 중 하나를 사용하여By dotting both sides of the last equality with the contravariant element ${\displaystyle {\hat {\mathbf {e} }}^{i}}$, we can conclude that ${\textstyle F^{i}={\hat {F}}^{i}/{\sqrt {g_{ii}}}}$. After substituting, the formula becomes:

${\displaystyle \operatorname {div} (\mathbf {F} )={\frac {1}{\rho }}{\frac {\partial \left({\frac {\rho }{\sqrt {g_{ii}}}}{\hat {F}}^{i}\right)}{\partial x^{i}}}={\frac {1}{\sqrt {\det g}}}{\frac {\partial \left({\sqrt {\frac {\det g}{g_{ii}}}}\,{\hat {F}}^{i}\right)}{\partial x^{i}}}.}$

자세한 내용은 § 곡선 좌표 참조.

특성.

다음의 성질은 모두 미적분학의 일반적인 분화 규칙에서 파생될 수 있다.가장 중요한 것은 이 분산이 선형 연산자, 즉,

${\displaystyle \mathbf {div}(a\mathbf {F} +b\mathbf {G})=a\operatorname {div} \mathbf {F} +b\opername {div} \mathbf {G}}}}$

모든 벡터 필드 F와 G 및 모든 실제 번호 a와 b에 대해.

type이 스칼라 값 함수이고 F가 벡터 필드인 경우 다음과 같은 유형의 제품 규칙이 있다.

${\displaystyle \operatorname {div}(\varphi \mathbf {F} )=\operatorname {grad} \varphi \cdot \mathbf {F} +\varphi \operatorname {div} \mathbf {F} ,},}}$

또는 더 선정적인 표기법으로.

${\displaystyle \nabla \cdot (\varbf {F} )=(\nabla \varphi )\cdot \mathbf {F} +\nabla \cdot \mathbf {F}).}$

두 벡터 필드 F와 G의 교차 곱을 3차원으로 하는 또 다른 제품 규칙은 컬을 포함하고 다음과 같이 읽는다.

${\displaystyle \operatorname {div}(\mathbf {G} ) (\mathbf {F} \mathbf {curl} \cdot \mathbf {G} -\cdot \operatorname {curl} \mathbf {G},},}}$

또는

${\displaystyle \nabla \cdot (\mathbf {G}) \time \mathbf {G}=(\nabla \mathbf {F} )\cdot \mathbf {G} -\mathbf \cdot (\nabla \time \mathbf {G}).}$

스칼라 필드의 라플라시안(Laplacian)은 필드의 구배(Gradition)가 서로 다른 것이다.

${\displaystyle \operatorname {div}(\operatorname {grad} \varphi )=\Delta \varphi .}$

벡터장(3차원의 경우)의 컬은 0과 같다.

$\\displaystyle \nabla \cdot(\nabla \time times \mathbf {F})=0.}$

R의³ 볼에 0의 발산성을 갖는 벡터 필드 F가 정의되면, 볼에 F = 컬 G를 가진 벡터 필드 G가 존재한다.R 지역의³ 경우 이보다 더 위상적으로 복잡한 경우, 후자의 진술이 거짓일 수 있다(Poincaré lema 참조).체인 콤플렉스의 호몰로 측정한 성명의 진실의 실패 정도

${\displaystyle \{{\text{scalar fields on }}U\}~{\overset {\operatorname {grad} }{\rightarrow }}~\{{\text{vector fields on }}U\}~{\overset {\operatorname {curl} }{\rightarrow }}~\{{\text{vector fields on }}U\}~{\overset {\operatorname {div} }{\rightarrow }}~\{{\text{scalar fields on }}U\}}$

기초 지역 U의 복잡성에 대한 훌륭한 계량화 역할을 한다.이것들은 드 람 코호몰로지(De Rham cohomology)의 시작이자 주요 동기들이다.

분해정리

R에서³ 연속적으로 2배 차이가 나고 r → ∞에 대해 충분히 빠르게 소멸되는 정지 플럭스 v(r)는 비회전성 파트 E(r)와 소스가 없는 파트 B(r)로 고유하게 분해될 수 있음을 보여줄 수 있다.또한 이러한 부품은 각각의 소스 밀도(위 참조)와 순환 밀도(Curl 기사 참조)에 의해 명확하게 결정된다.

한 사람이 가지고 있는 비역전적인 것이다.

${\displaystyle \mathbf {E} =-\nabla \Phi(\mathbf {r}),}$

와 함께

${\displaystyle \Phi (\mathbf {r} )=\int _{\mathbb {R} ^{3}}\,d^{3}\mathbf {r} '\;{\frac {\operatorname {div} \mathbf {v} (\mathbf {r} ')}{4\pi \left \mathbf {r} -\mathbf {r} '\right }}.}$

소스가 없는 부분 B도 마찬가지로 쓸 수 있다: 스칼라 전위 φ(r)을 벡터 전위 A(r)로 대체하고 - -φφ by + + × A라는 용어로만 교체하면 되며, 소스 밀도 div v는 순환 밀도 ∇ × v.

이 "배열정리"는 전자역학의 정지된 경우의 부산물이다.그것은 보다 일반적인 헬름홀츠 분해의 특별한 경우로서, 3개 이상의 차원에서도 작용한다.

임의 치수

벡터 장의 차이는 어떤 치수로도 정의될 수 있다.만약

${\displaystyle \mathbf {F} =(F_{1},F_{2},\ldots F_{n}),}$

좌표 x₁, x₂, ..., x가_n 있는 유클리드 좌표계에서 정의한다.

${\displaystyle \operatorname {div} \mathbf {F} =\nabla \cdot \mathbf {F} ={\frac {\partial F_{1}}{\partial x_{1}}}+{\frac {\partial F_{2}}{\partial x_{2}}}+\cdots +{\frac {\partial F_{n}}{\partial x_{n}}}.}$

1차원의 경우 F는 정규함수로 감소하고, 그 차이는 파생상품으로 감소한다.

어떤 n에 대해서도, 그 차이는 선형 연산자로, 「제품 규칙」을 만족한다.

${\displaystyle \nabla \cdot (\varvi \mathbf {F})=(\nabla \varphi )\cdot \mathbf {F} +\nabla \cdot \mathbf {F}}}}}}$

모든 스칼라 값 함수 φ에 대해.

외부 파생 모델과의 관계

R의³ 3형식으로 2형식을 갖는 외부 파생상품의 특별한 경우로서 그 차이를 표현할 수 있다.현재 2-폼을 다음으로 정의

$dy\wedge dz+, dy\displaystyle j=F_{1}\,dy\wedge dz+F_{2}\,dz\wedge dx+F_{3}\,dx\wedge dy.}$

velocity = 1 dx dy dy ∧ dz의 밀도 ρ = 1 dx dy ∧ dz의 "스퍼프"로 단위 시간 당 표면을 흐르는 "스퍼프"의 양을 측정한다.그 외부 파생상품 dj는 그 다음 에 의해 주어진다.

${\displaystyle dj=\left({\frac {\partial F_{1}}{\partial x}}+{\frac {\partial F_{2}}{\partial y}}+{\frac {\partial F_{3}}{\partial z}}\right)dx\wedge dy\wedge dz=(\nabla \cdot {\mathbf {F} })\rho }$

여기서 $\wedge {\displaystyle }$ ${\displaystyle \wedge}$은(는) 쐐기 제품이다.

따라서 벡터장 F의 차이는 다음과 같이 표현할 수 있다.

${\displaystyle \nabla \cdot {\mathbf {F}}={\star }{\big (}{\mathbf {F}^{\flat }{\big )}.}$

여기서 위첨자 ♭은 두 가지 음악적 이형체 중 하나이며, ⋆은 호지 스타 운영자 이다.이런 식으로 발산문을 쓰면 연산자 $\star {\displaystyle }$ ${\displaystyle d}$ ${\displaystyle \star }$ ${\${\star $}d{\$star }}}}을(를) 코드프렌더라고 한다$$.현재 2-폼과 외부 파생상품으로 작업하는 것이 벡터장 및 분산으로 작업하는 것보다 쉬운데, 이는 차이와 달리 외부 파생상품은 (커비린) 좌표계의 변경과 통하기 때문이다.

곡선 좌표

적절한 표현은 곡선 좌표가 더 복잡하다.벡터장의 분비는 리만 또는 로렌츠 다지관과 같은 체적 형태(또는 밀도) μ를 갖는 차원 n의 어떤 다른 다지관까지 자연스럽게 확장된다.그러한³ 다지관의 벡터장에 대한 2-폼의 구성을 일반화하면서 벡터 필드 X는 X를 μ로 수축하여 얻은 (n - 1)-폼_X j = i μ를 정의한다.그 차이는 다음에 정의되는 함수가 된다.

${\displaystyle dj=(\operatorname {div}X)\mu .}$

차이점은 다음과 같이 Lie 파생상품의 관점에서 정의될 수 있다.

${\displaystyle {\mathcal {L}_{X}\mu =(\operatorname {div}X)\mu .}$

이는 발산량이 벡터장과 함께 흐를 때 부피 단위(부피 요소)의 팽창 속도를 측정한다는 것을 의미한다.

사이비-리만 다지관에서는 볼륨에 관한 차이를 레비-시비타 연결 ∇의 관점에서 표현할 수 있다.

${\displaystyle \operatorname {div}X=\nabla \cdot X={X^{a}_{;a}}$

여기서 두 번째 표현식은 자신과 함께 1-폼 ∇X로 평가되는 벡터장의 수축이고 마지막 표현은 Ricci 미적분학의 전통적인 좌표식이다.

연결을 사용하지 않는 등가 표현식은

${\displaystyle \operatorname {div}(X)={\frac {1}{\sqrt}{\det g\오른쪽}\,\partial _{a}\{\sqrt({\partial \\\\\\\det detect g\\}\rift}\{\rift}\right}}},X^{a}$

여기서 g는 미터법이고 $\partial {\displaystyle {\mathrm{}}_{}}$는 ${\$는^a x 좌표에 관한 부분파생물을 나타낸다$$.차이점은 부피에 대한 정확한 개념으로 작성되어야 하기 때문에 (의 결정 인자의 절대값) 측정지표의 제곱근은 나타난다.root)이 나타난다.곡선 좌표에서 기본 벡터는 더 이상 정형화된 것이 아니다. 결정 인자는 이 경우 부피에 대한 올바른 개념을 암호화한다.여기서, 여기서, 한 번, ${\displaystyle X^{}}$ $a{\displaystyle {}^{}}$ ${\$ X$^{a}}$를 "평평한 공간"(좌표가 실제로 직교된 공간)으로 변환할 수 있도록$$, 그리고 다시 한 번 ${$ {\$displaysty \partial _{a}$도 "평평평평평한 공간"으로 변환할 수 있도록 나타나 있다.평탄한 공간에서의 볼륨 개념(즉, 단위 볼륨, 즉 하나, 즉 기록되지 않음)분모에 제곱근(square-root)이 나타나는데, 이는 파생상품이 벡터(공변량)로 반대(반대)로 변하기 때문이다.국지적인 계산이 전통적인 방법으로 이루어질 수 있는 "평평한 좌표계"에 도달하는 이 생각을 비엘베인이라고 한다.이것을 보는 또 다른 방법은 그 차이가 변장의 코디프렌더라는 것을 알아두는 것이다.즉, 이 차이는 ${\displaystyle d}$ ${\displaystyle \star }$ d$display$ {\$displaystyle$ \$star }$과($와$) d ${\displaystyle d}$과(와) $\star {\displaystyle }$ ${\displaystyle \star }$의 표현에 해당된다.호지 별은 그것의 구성으로 인해 볼륨 형태가 모든 적절한 장소에 나타나게 한다.

텐서의 차이

차이점은 또한 텐더에 일반화될 수 있다.아인슈타인 표기법에서, 반대 벡터 F의^μ 차이는 다음과 같다.

${\displaystyle \nabla \cdot \mathbf {F} =\nabla _{\mu ^{\mu }}}$

여기서 ∇_μ은 공변량 파생물을 나타낸다.이 일반적인 설정에서, 분리의 올바른 공식화는 그것이 코디프렌더라는 것을 인식하는 것이다. 적절한 성질은 거기서 나온다.

동등하게, 일부 저자들은 음악적 이형성 ♯을 사용하여 혼합 텐서의 분산을 정의한다: T가 (p, q)-텐서(contractariant 벡터 p, 공변량 q)-텐서라면 T의 분산을 (p, q - 1)텐서라고 정의한다.

${\displaystyle (\operatorname {div} T)(Y_{1},\ldots ,Y_{q-1})={\operatorname {trace} }{\Big (}X\mapsto \sharp (\nabla T)(X,\cdot ,Y_{1},\ldots ,Y_{q-1}){\Big )};}$

즉, 공변량 파생상품의 처음 두 공변량 지수에 대한 추적을 취한다.^[a]$♯{\displaystyle \mathrm{}}$ ${\displaystyle \sharp }$ 기호는$$ 음악적 이형성을 가리킨다.

에 대한 일련의 기사의 일부
미적분학.
기본 정리 라이프니즈 적분 규칙 함수의 한계 연속성 평균값 정리 롤의 정리
미분 정의들 파생상품(일반화) 미분 극소수의 함수의. 총계 개념 분화 표기법 제2차 파생상품 암묵적 분화 로그 분화 관련금리 테일러의 정리 규칙 및 ID 합계 제품 체인 힘 지수 라피탈의 법칙 반비례 라이프니즈 장군 파아디 브루노 공식 레이놀즈.
적분 통합 목록 적분 변환 정의들 해독제 적분(불량) 리만 적분 르베그 통합 등고선 통합 역함수의 적분 통합 기준 부품. 디스크 원통 조개 대체(트리거, 위어스트라스, 오일러) 오일러의 공식 부분분수 순서변경 환원공식 통합 기호 아래 차별화 리스치 알고리즘
시리즈 기하학(산술-기하계) 조화 교대로 힘 이항체 테일러 수렴시험 합계한계(기간시험) 비율 뿌리 적분 직접 비교 한계비교 교대계열 코시 응결 디리클레 아벨
벡터 그라데이션 발산 컬 라플라시안 방향파생상품 정체성 정리 그라데이션 그린스 스톡스 발산 일반화 스톡스
다변량 형식주의 매트릭스 텐서 외부 기하학 정의들 부분파생상품 다중 적분 라인 적분 표면 적분 부피 적분 야코비안 헤시안
전문화된 분수 말리아빈 스토카스틱 변형
잡다한 프레살쿨루스 역사 용어집 주제 목록 통합 비 분석
v t

참고 항목

• 컬
• 원통형 및 구형 좌표 분석
• 발산정리
• 그라데이션

메모들

인용구

참조

• Brewer, Jess H. (1999). "DIVERGENCE of a Vector Field". musr.phas.ubc.ca. Archived from the original on 2007-11-23. Retrieved 2016-08-09.
• Rudin, Walter (1976). Principles of mathematical analysis. McGraw-Hill. ISBN 0-07-054235-X.
• Edwards, C. H. (1994). Advanced Calculus of Several Variables. Mineola, NY: Dover. ISBN 0-486-68336-2.
• Gurtin, Morton (1981). An Introduction to Continuum Mechanics. Academic Press. ISBN 0-12-309750-9.
• Korn, Theresa M.; Korn, Granino Arthur (January 2000). Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review. New York: Dover Publications. pp. 157–160. ISBN 0-486-41147-8.

외부 링크

위키미디어 커먼즈에는 다이버전스와 관련된 미디어가 있다.

• "Divergence", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• 벡터장 발산 사상
• 칸 아카데미: 다이버전스 비디오 레슨
• Sanderson, Grant (June 21, 2018). "Divergence and curl: The language of Maxwell's equations, fluid flow, and more". 3Blue1Brown. Archived from the original on 2021-12-11 – via YouTube.