큐브
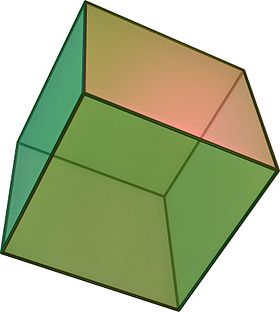
Cube| 정육면체 | |
|---|---|
 (회전 모델을 보려면 여기를 클릭) | |
| 유형 | 플라톤 고체 |
| 쇼트 코드 | 4= |
| 요소들 | F = 6, E = 12 V = 8 (표준 = 2) |
| 측면 나란히 | 6{4} |
| 콘웨이 표기법 | C |
| 슐레플리 기호 | {4,3} |
| t{2,4} 또는 {4}×{} tr{2,2} 또는 {}×{}×{} | |
| 얼굴 구성 | V3.3.3 |
| 위토프 기호 | 3 2 4 |
| 콕서터 다이어그램 | |
| 대칭 | Oh, B3, [4,3], (*432) |
| 로테이션 그룹 | O, [4,3]+, (432) |
| 레퍼런스 | U06, C18, W3 |
| 특성. | 정칙 볼록조네이드 |
| 이면각 | 90° |
 4.4.4 (버텍스 그림) |  팔면체 (입체 다면체) |
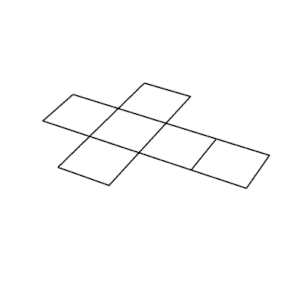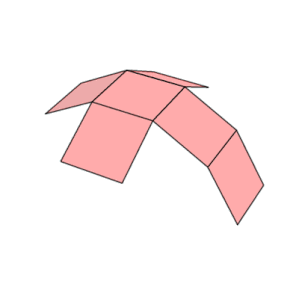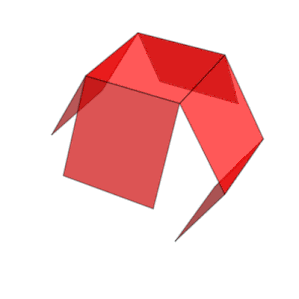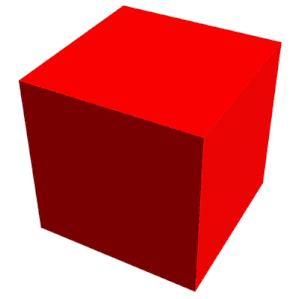
 그물 | |
기하학에서, 큐브는[1] 6개의 정사각형 면, 면 또는 변으로 둘러싸인 3차원 입체 객체이며, 각 정점에 3개의 만남이 있습니다.
입방체는 유일한 정육면체이며 5개의 플라톤 고체 중 하나입니다.면 6개, 모서리 12개, 정점 8개가 있습니다.
또한 정육면체는 정사각형이고, 정삼각형이며, 오른쪽 마름모꼴은 3-zone면체이다.그것은 세 방향의 정사각형 프리즘과 네 방향의 삼각삼각형이다.
입방체는 팔면체와 쌍대이다.그것은 입방체 또는 팔면체 대칭을 가지고 있다.
입방체는 면이 모두 정사각형인 유일한 볼록 다면체이다.
직교 투영
입방체에는 정점, 모서리, 면 및 정점 도형에 대한 법선을 중심으로 네 개의 특수 직교 투영부가 있습니다.첫 번째와 세 번째가2 A와2 B 콕서터 평면에 해당합니다.
| 중심 | 얼굴 | 꼭지점 |
|---|---|---|
| 콕서터 비행기 | B2.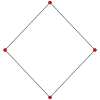 | A2.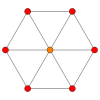 |
| 투사적 대칭 | [4] | [6] |
| 기울어진 보기 | 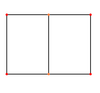 |  |
구면 타일링
큐브는 구형 타일링으로 표현될 수 있으며 입체 투영을 통해 평면에 투영될 수 있습니다.이 투영법은 적합하며 각도는 보존되지만 면적이나 길이는 보존되지 않습니다.구면의 직선은 평면에 원형 호로 투영됩니다.
 |  |
| 맞춤법 투영법 | 입체 투영 |
|---|
데카르트 좌표
원점을 중심으로 모서리가 축에 평행하고 모서리 길이가 2인 입방체의 경우 정점의 데카르트 좌표는 다음과 같습니다.
- (±1, ±1, ±1)
내부는 모든 점(x0, x1, x2)으로 구성되며 모든 i에 대해 -1 < xi < 1이다.
3차원 공간의 방정식
해석 기하학에서 중심(x0, y0, z0)과 모서리 길이가 2a인 입방체의 표면은 다음과 같이 모든 점(x, y, z)의 궤적이 된다.
세 지수 모두가 무한대에 가까워짐에 따라 입방체는 또한 3D 초연립체의 한계 사례로 간주될 수 있다.
수식
모서리 의 입방체a의 경우 {\ a
| 표면적 | 용량 | ||
| 대각선 | 공간 대각선 | ||
| 외접구 반지름 | 모서리에 접하는 구의 반지름 | ||
| 내접구 반지름 | 면 사이의 각도(라디안 단위) |
정육면체의 부피는 변의 3제곱 × a × a × × 이므로, 정사각형 및 2제곱과 같이 3제곱이라고 합니다.
정육면체는 주어진 표면적을 가진 정육면체(사각형 상자) 중에서 부피가 가장 큽니다.또한 큐브는 총 선형 크기(길이+폭+높이)가 동일한 큐보이드 중에서 가장 큰 볼륨을 가집니다.
스페이스 포인트
외접구가 반지름 R을 갖는 입방체의 경우, 그리고 입방체의 8개의 꼭지점으로부터의 거리i d가 있는 3차원 공간의 특정 지점에 대해 다음과 같은 [2]값을 갖는다.
큐브를 2배로 하다
큐브를 두 배로 하는 것, 즉 델리안 문제는 고대 그리스 수학자들이 제기했던 문제였는데, 이 문제는 주어진 큐브의 모서리 길이부터 시작해서 원래의 큐브의 두 배 부피로 큐브의 모서리 길이를 구성하기 위해서 나침반과 직선만 사용했다.그들은 이 문제를 풀 수 없었고, 1837년 피에르 원첼은 2의 세제곱근은 구성 가능한 수가 아니기 때문에 불가능하다는 것을 증명했다.
균일한 색채와 대칭

입방체에는 3가지 균일한 색상이 있으며, 각 정점 주변의 정사각형 면의 색상으로 이름이 붙여집니다: 111, 112, 123.
정육면체는 네 가지 대칭 클래스가 있으며, 정점-추이적 색칠로 나타낼 수 있습니다.가장 높은 팔면체 대칭h O는 모든 면의 색이 같다.이면체 대칭4h D는 6개의 면이 모두 다른 색상으로 된 입체 입방체에서 유래합니다.프리즘 서브셋2d D는 기존과 같은 색상으로2h, D는 반대쪽과 짝을 이루는 총 3가지 색상으로 변을 번갈아 색상으로 했다.각 대칭 형태에는 서로 다른 와이토프 기호가 있습니다.
| 이름. | 규칙적인. 육면체 | 사각 프리즘 | 직사각형 사다리꼴 | 직사각형 입방체 | 마름모꼴 프리즘 | 삼각형의 삼면체 |
|---|---|---|---|---|---|---|
| 콕서터 도표 | ||||||
| 슐레플리 기호. | {4,3} | {4}×{ } rr{4,2} | s2{2,4} | { }3 tr{2,2} | { }×2{ } | |
| 와이토프 기호. | 3 4 2 | 4 2 2 | 2 2 2 | |||
| 대칭 | 오h [4,3] (*432) | D4h. [4,2] (*422) | D2d. [4,2+] (2*2) | D2h. [2,2] (*222) | D3d. [6,2+] (2*3) | |
| 대칭 주문 | 24 | 16 | 8 | 8 | 12 | |
| 이미지 (비활성화) 색칠) |  (111) |  (112) |  (112) |  (123) |  (112) |  (111), (112) |
기하 관계

큐브에는 11개의 그물이 있습니다(위 그림 1개). 즉, [3]7개의 모서리를 잘라 중공 큐브를 평평하게 만드는 방법은 11가지가 있습니다.인접한 두 면이 같은 색을 가지지 않도록 큐브를 색칠하려면 적어도 세 가지 색상이 필요합니다.
입방체는 3차원 유클리드 공간의 유일한 규칙 타일링 셀이다.그것은 또한 짝수의 변을 가진 면을 가지고 있다는 점에서 플라톤 고체들 사이에서 독특하며, 결과적으로 그것은 그 군에서 유일한 조노면체 구성원이다(모든 면이 점 대칭을 가지고 있다).
그 입방체는 6개의 동일한 정사각형 피라미드로 잘릴 수 있다.이 정사각형 피라미드를 두 번째 입방체의 면에 부착하면 마름모꼴 12면체를 얻을 수 있다(코프라나 삼각형의 쌍이 마름모꼴 면에 결합됨).
기타 치수
4차원 유클리드 공간에서의 입방체의 유사체는 특별한 이름인 테서랙트 또는 하이퍼큐브를 가지고 있다.보다 적절하게, 하이퍼 큐브(또는 단순히 n차원 큐브 또는 n-큐브)는 n차원 유클리드 공간에서 큐브의 유사체이고, 테서랙트는 4차 하이퍼 큐브이다.하이퍼큐브는 측정 폴리토프라고도 불립니다.
저차원의 입방체도 있습니다.즉, 0차원의 점, 1차원의 선분, 2차원의 정사각형입니다.
관련 다면체

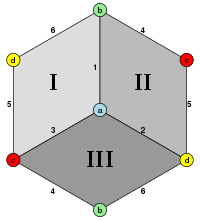
대척지도에 의한 입방체의 몫은 투영 다면체, 즉 반구체를 생성한다.
원본 큐브의 모서리 길이가 1인 경우, 해당 이중 다면체(팔면체)의 모서리 는 2/({입니다.
큐브는 다양한 종류의 일반 다면체에서 특별한 경우입니다.
| 이름. | 엣지 길이가 같습니까? | 등각? | 직각이요? |
|---|---|---|---|
| 큐브 | 네. | 네. | 네. |
| 마름모꼴 | 네. | 네. | 아니요. |
| 입방체 | 아니요. | 네. | 네. |
| 평행관 | 아니요. | 네. | 아니요. |
| 사변면 육면체 | 아니요. | 아니요. | 아니요. |
정육면체의 꼭지점은 각각 정4면체를 이루는 4개의 두 그룹으로 그룹화될 수 있습니다. 더 일반적으로 이것은 데미큐브라고 불립니다.이 둘은 함께 정규 화합물인 스텔라 옥탄굴라를 형성합니다.그 둘의 교점은 정팔면체를 이룬다.정사면체의 대칭은 각 사면체를 자신에게 매핑하는 정육면체의 대칭과 일치하고, 정육면체의 다른 대칭은 두 정육면체를 서로 매핑합니다.
그러한 정4면체 중 하나는 다음과 같은 부피를 가진다.큐브의 1/3입니다.나머지 공간은 각각 큐브의 1/6 부피의 4개의 동일한 불규칙 사면체로 구성됩니다.
정류된 입방체는 정육면체이다.더 작은 모서리를 잘라내면 6개의 팔각형 면과 8개의 삼각형 면을 가진 다면체를 얻을 수 있습니다.특히 우리는 정규 8각형을 얻을 수 있다.마름모꼴 팔면체는 모서리와 모서리를 모두 정확한 양으로 잘라내면 얻을 수 있습니다.
정육면체는 정육면체의 각 정점이 12면체의 정점이 되고 각 모서리가 12면체의 면 중 하나의 대각선이 되도록 12면체에 새겨질 수 있다. 이러한 모든 정육면체를 취하면 5개의 정육면체의 정육면체가 된다.
정육면체의 반대쪽 모서리 2개가 직접 연결된 3개의 정점의 깊이에서 잘리면 불규칙한 8면체를 얻을 수 있다.이 불규칙한 팔면체 중 8개는 정팔면체의 삼각면에 부착되어 정팔면체를 얻을 수 있다.
입방체는 일련의 구면 다면체와 순서 3 정점 도형을 가진 타일링과 위상적으로 관련이 있습니다.
| *n32 정규 타일링 대칭 변환: {n,3} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 구면 | 유클리드 | 콤팩트 쌍곡선 | 파라코 | 비콤팩트 쌍곡선 | |||||||
 |  |  |  |  |  |  |  |  |  |  |  |
| {2,3} | {3,3} | {4,3} | {5,3} | {6,3} | {7,3} | {8,3} | {∞,3} | {12i,3} | {9i,3} | {6i,3} | {3i,3} |
정육면체는 정팔면체와 정팔면체와 관련된 균일한 다면체 계열 중 하나이다.
| 균일한 팔면체 다면체 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 대칭: [4,3], (*432) | [4,3]+ (432) | [1+,4,3] = [3,3] (*332) | [3+,4] (3*2) | |||||||
| {4,3} | t{4,3} | r{4,3} r{31,1} | t{3,4} t{31,1} | {3,4} {31,1} | rr{4,3} s2{3,4} | tr{4,3} | sr{4,3} | h{4,3} {3,3} | h2{4,3} t{3,3} | s{3,4} s{31,1} |
= | = | = | ||||||||
| 이중에서 균일한 다면체 | ||||||||||
| V43 | V3.82 | V(3.4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.62 | V35 |
정육면체는 규칙 타일링 시퀀스의 일부로 위상적으로 관련되며, 쌍곡면으로 확장됩니다: {4,p}, p=3,4,5...
| *n42 정규타일링 대칭변환: {4,n} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 구면 | 유클리드 | 콤팩트 쌍곡선 | 파라콤팩트 | ||||||||
 {4,3} |  {4,4} |  {4,5} |  {4,6} |  {4,7} |  {4,8}... |  {4,∞} | |||||
이면체 대칭인4 Dih에서 입방체는 일련의 균일한 다면체와 타일링 4.2n.2n으로 위상적으로 관련지어져 쌍곡면까지 확장된다.
| *n42 잘린 타일링 대칭 돌연변이: 4.2n.2n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 대칭 *n42 [n,4] | 구면 | 유클리드 | 콤팩트 쌍곡선 | 파라콤프 | |||||||
| *242 [2,4] | *342 [3,4] | *442 [4,4] | *542 [5,4] | *642 [6,4] | *742 [7,4] | *842 [8,4]... | *∞42 [∞,4] | ||||
| 잘렸다 수치 |  |  |  |  |  |  |  |  | |||
| 설정. | 4.4.4 | 4.6.6 | 4.8.8 | 4.10.10 | 4.12.12 | 4.14.14 | 4.16.16 | 4.∞.∞ | |||
| n개 수치 |  |  |  |  |  |  |  |  | |||
| 설정. | V4.4.4 | V4.6.6 | V4.8.8 | V4.10.10 | V4.12.12 | V4.14.14 | V4.16.16 | V4.★★ | |||
이 모든 그림들은 팔면체 대칭을 가지고 있다.
입방체는 일련의 마름모꼴 다면체와 [n,3] 콕서터 군 대칭을 가진 타일링의 일부이다.입방체는 마름모가 정사각형인 마름모꼴 육면체로 볼 수 있다.
| 이중 준규격 타일링 대칭 돌연변이: V(3.n)2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| *n32 | 구면 | 유클리드 | 쌍곡선 | ||||||||
| *332 | *432 | *532 | *632 | *732 | *832... | *∞32 | |||||
| 타일링 |  |  |  |  |  |  |  | ||||
| 컨피규정. | V(3.3)2 | V(3.4)2 | V(3.5)2 | V(3.6)2 | V(3.7)2 | V(3.8)2 | V(3.★)2 | ||||
큐브는 정사각형 프리즘입니다.
| 균등-곤 프리즘 계열 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 프리즘명 | 디지널 프리즘 | (트리거) 삼각 프리즘 | (사각형) 사각 프리즘 | 오각 프리즘 | 육각 프리즘 | 칠각 프리즘 | 팔각 프리즘 | 에네오갈 프리즘 | 십각형 프리즘 | 헨데카날 프리즘 | 도데카날 프리즘 | ... | 편평 프리즘 |
| 다면체 이미지 | ... | ||||||||||||
| 구형 타일 이미지 | 평면 타일 이미지 | ||||||||||||
| 정점 설정 | 2.4.4 | 3.4.4 | 4.4.4 | 5.4.4 | 6.4.4 | 7.4.4 | 8.4.4 | 9.4.4 | 10.4.4 | 11.4.4 | 12.4.4 | ... | ∞.4.4 |
| 콕서터 다이어그램 | ... | ||||||||||||
삼각삼면체로서, 입방체는 육각형 이면체 대칭족과 관련이 있다.
| 균일한 육면체 이면체 구면 다면체 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 대칭: [6,2], (*622) | [6,2]+, (622) | [6,2+], (2*3) | ||||||||||||
 |  |  |  |  |  |  | ||||||||
| {6,2} | t{6,2} | r{6,2} | t{2,6} | {2,6} | rr{6,2} | tr{6,2} | sr{6,2} | s{2,6} | ||||||
| 복식부터 제복까지 | ||||||||||||||
 |  |  |  |  |  |  |  |  | ||||||
| V62 | V122 | V62 | V4.4.6 | V26 | V4.4.6 | V4.4.12 | V3.3.6 | V3.3.3 | ||||||
 3개의 큐브 화합물 |  5개의 큐브 화합물 |
균일한 벌집과 폴리코라 차림
| 큐빅 벌집 | 잘린 정사각형 프리즘 벌집 | 스너브 사각 프리즘 벌집 | 가늘고 긴 삼각형 프리즘 벌집 | 자이로롱꼴 삼각형 프리즘 벌집 |
 |  |  |  |  |
| 통조림 큐빅 벌집 | 칸티트란크 큐빅 벌집 | 런시트런치드 큐빅 벌집 | 런케이트 대체 큐빅 벌집 | |
 |  |  |  |
또한 5개의 4차원 균일한 폴리코라의 요소이기도 합니다.
| 테서랙트 | 캔텔레이티드 16셀 | 룬케이티드 정삼각형 | 칸티트런 절단된 16셀 | Runcitruncated 16 셀 |
 |  |  |  |  |
입방체 그래프
| 입방체 그래프 | |
|---|---|
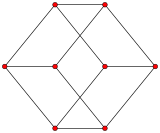 | |
| 의 이름을 따서 명명됨 | 질문3 |
| 꼭지점 | 8 |
| 가장자리 | 12 |
| 반지름 | 3 |
| 직경 | 3 |
| 둘레 | 4 |
| 자기동형 | 48 |
| 색수 | 2 |
| 특성. | 해밀턴, 규칙, 대칭, 거리-규칙, 거리-추이, 3-vertex 연결, 이분, 평면 그래프 |
| 그래프 및 매개 변수 표 | |
큐브의 골격(정점과 모서리)은 큐브 그래프라고 하는 8개의 정점과 12개의 모서리를 가진 그래프를 형성합니다.하이퍼큐브 [4]그래프의 특수한 경우입니다.5개의 플라톤 그래프 중 하나이며, 각 그래프는 플라톤 고체의 골격입니다.
확장은 3차원 k-ARY 해밍 그래프이며, k = 2의 경우 입방체 그래프이다.이러한 종류의 그래프는 컴퓨터의 병렬 처리 이론에서 발생합니다.
「 」를 참조해 주세요.
레퍼런스
- ^ 고대 프랑스어 '라틴 큐부스' '그리스어 'β β ο ο ( kubos)'에서 온 영어 큐브. '큐브, 다이스, 척추'라는 뜻이다.PIE *keu(b)-부터 차례로 "굽혀서 돌리다".
- ^ 박, 푸성."정규 폴리토프 거리", 포럼 지오메트리컬럼 16, 2016, 227-232.http://forumgeom.fau.edu/FG2016volume16/FG201627.pdf Wayback Machine에서 2016-10-10년 아카이브 완료
- ^ Weisstein, Eric W. "Cube". MathWorld.
- ^ Weisstein, Eric W. "Cubical graph". MathWorld.
외부 링크
- Weisstein, Eric W. "Cube". MathWorld.
- 큐브: 인터랙티브 다면체 모델*
- 대화형 애니메이션이 있는 큐브의 볼륨
- 큐브(로버트 웹 사이트)
| 가족 | An | Bn | I2(p) / Dn | E6/E7/E8/F4/G2 | Hn | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 정다각형 | 삼각형 | 광장 | p곤 | 육각형 | 펜타곤 | |||||||
| 균일한 다면체 | 사면체 | 8면체 • 큐브 | 데미큐브 | 12면체 • 이십면체 | ||||||||
| 균일한 폴리코론 | 펜타코론 | 16 셀 • 테서랙트 | 데모테서랙트 | 24 셀 | 120 셀 • 600 셀 | |||||||
| 균일한 5 폴리토프 | 51200x | 5 - ORTOPLEX • 5 - 큐브 | 5 데미큐브 | |||||||||
| 균일한 6 폴리토프 | 61200x | 6-정류 • 6-큐브 | 6-데미큐브 | 122 • 221 | ||||||||
| 균일한 7 폴리토프 | 71200x | 7-정류 • 7-큐브 | 7 데미큐브 | 132 • 231 • 321 | ||||||||
| 균일한 8 폴리토프 | 8180x | 8-정류 • 8-큐브 | 8개의 데미큐브 | 142 • 241 • 421 | ||||||||
| 균일한 9-폴리토프 | 9169x | 9-정류 • 9-입방체 | 9데미큐브 | |||||||||
| 균일한 10 폴리토프 | 10-1996x | 10 - ORTOPLEX • 10 - 큐브 | 10 데미큐브 | |||||||||
| 균일한 n-폴리토프 | n-1996x | n-ortoplex • n-입방체 | n-데미큐브 | 1k2 • 2k1 • k21 | n-오각형 폴리토프 | |||||||
| 주제: 폴리토프 패밀리 • 일반 폴리토프 • 일반 폴리토프 및 화합물 목록 | ||||||||||||