정육면체 3개 혼합물
Compound of three cubes| 정육면체 3개 혼합물 | |
|---|---|
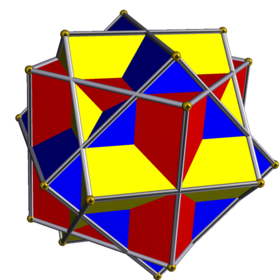 | |
| 유형 | 균일 화합물 |
| 색인 | UC8 |
| 볼록 선체 | 통일형 잘린 팔면체 |
| 폴리헤드라 | 큐브 3개 |
| 얼굴 | 6+12 제곱 |
| 가장자리 | 36 |
| 정점 | 24 |
| 대칭군 | 팔면체(Oh) |
| 하나의 구성 요소로 제한되는 부분군 | 4배 프리즘(D4h) |
기하학에서 세 개의 정육면체의 화합물은 팔면 대칭으로 배열된 세 개의 정육면체에서 형성된 균일한 다면체 화합물이다.[1]맥스 브뤼크너와 엠씨 에셔의 작품에서 묘사되어 왔다.
역사
이 화합물은 막스 브뤼크너의 저서 '비엘레케 und Vielflache(1900)'에,[2] 브뤼크너의 책에서 이를 알게 된 엠씨 에셔의 석판 인쇄 폭포(1961년)에 등장한다.그것의 이중, 3개의 옥타헤드라의 합성어로, 초기 에셔 목판화의 중심 이미지를 형성한다.[3]
15세기 필사본 드 퀸케코모니버스 레귤러버스에서 피에로 델라 프란체스카는 정육면체 둘레에 8개의 정육면체 모서리가 8개의 면에 놓여 있는 8개의 정육면체 그림을 담고 있다.한 옥타헤드론 안에 이렇게 새겨진 세 개의 정육면체는 세 개의 정육면체의 혼합물을 형성하지만 델라 프란체스카는 그 혼합물을 묘사하지 않는다.[4]
드 퀸케코모네버스 정규버스 8각형 큐브
8면체 내 큐브의 또 다른 보기
시공 및 좌표
이 화합물은 세 개의 동일한 정육면체를 중첩시킨 다음 각각을 45도씩 별도의 축을 중심으로 회전시켜 만들 수 있다(두 개의 반대 면의 중심을 통과한다.[3]
이 화합물의 정점에 대한 데카르트 좌표는(± ,± ) (0,\1,\의 모든 순열로 선택할 수 있다
참조
- ^ Verheyen, Hugo F. (1996), "Chapter 4: Classification of the finite compounds of cubes", Symmetry Orbits, Design Science Collection, Boston: Birkhäuser, pp. 95–159, doi:10.1007/978-1-4612-4074-7_5, ISBN 0-8176-3661-7, MR 1363715; 특히 페이지 136을 보라.
- ^ Brückner, Max (1900), Vielecke und Vielflache, Theorie und Geschichte, Leipzig: B.G. Teubner, Plate 23
- ^ a b Hart, George W., "Max Brücknerʼs Wunderkammer of Paper Polyhedra", Bridges 2019 Conference Proceedings (PDF), pp. 59–66
- ^ Hart, George W. (1998), "Piero della Francesca's Polyhedra", Virtual Polyhedra.





