벡터공간

수학과 물리학에서 벡터 공간(, linear space)은 흔히 벡터라고 불리는 원소들이 더해지고 스칼라라고 불리는 숫자들에 곱해질 수 있는 집합입니다. 스칼라는 종종 실수이지만 복소수일 수도 있고, 더 일반적으로 모든 필드의 요소일 수도 있습니다. 벡터 덧셈과 스칼라 곱셈의 연산은 벡터 공리라고 불리는 특정 요구 사항을 충족해야 합니다. 실수 벡터 공간과 복소 벡터 공간은 실제 좌표 공간 또는 복소 좌표 공간과 같은 다양한 종류의 스칼라에 기반한 일종의 벡터 공간입니다.

벡터 공간은 유클리드 벡터를 일반화하여 힘과 속도와 같은 물리량을 모델링할 수 있으며, 이를 통해 크기뿐만 아니라 방향도 가질 수 있습니다. 벡터 공간의 개념은 벡터 공간에서 계산을 허용하는 행렬의 개념과 함께 선형 대수의 기본입니다. 이것은 선형 방정식의 시스템을 조작하고 연구하는 간결하고 종합적인 방법을 제공합니다.

벡터 공간은 대략적으로 말하면 공간에서 독립적인 방향의 수를 지정하는 차원으로 특징지어집니다. 이것은 주어진 필드 위에 동일한 차원을 갖는 두 벡터 공간에 대해 벡터-공간 구조에만 의존하는 속성이 정확히 동일하다는 것을 의미합니다(기술적으로 벡터 공간은 동형입니다). 벡터 공간은 그 차원이 자연수일 경우 유한 차원입니다. 그렇지 않으면, 그것은 무한 차원이고, 그것의 차원은 무한 기수입니다. 유한 차원 벡터 공간은 기하학 및 관련 영역에서 자연스럽게 발생합니다. 무한 차원 벡터 공간은 수학의 많은 영역에서 발생합니다. 예를 들어, 다항식 고리는 셀 수 없이 많은 무한 차원 벡터 공간이며, 많은 함수 공간은 연속체의 카디널리티를 차원으로 갖습니다.

수학에서 고려되는 많은 벡터 공간들은 또한 다른 구조를 가지고 있습니다. 이것은 필드 확장, 다항식 고리, 연관 대수 및 리 대수를 포함하는 대수의 경우입니다. 이것은 함수 공간, 내부 곱 공간, 정칙 공간, 힐베르트 공간, 바나흐 공간을 포함하는 위상 벡터 공간의 경우이기도 합니다.

대수적 구조
그룹 같은 그룹. 세미그룹 / 모노이드 랙 앤 쿼들 준군과 고리 아벨 군 마그마 거짓말군 군론
반지같은 울리다 Rng 세미링 니어링 교환환 도메인 적분영역 들판 나눗셈링 거짓말 고리이론
격자형 격자 세미라티스 보체격자 총주문량 헤이팅 대수 부울 대수 격자 지도 격자이론
모듈형 모듈 연산자가 있는 그룹 벡터공간 선형대수학
대수적 대수학 협회 비연관적 합성대수학 거짓말 대수 등급화 쌍대뇌 호프 대수학
v t

정의 및 기본 속성

이 글에서는 벡터를 굵은 글씨로 표현하여 스칼라와 구분하고자 합니다.^{[nb 1][1]}

필드 F 위의 벡터 공간은 아래 나열된 8개의 공리를 만족하는 이진 연산 및 이진 함수와 함께 비어 있지 않은 집합 V입니다. 이런 맥락에서 흔히 V의 원소를 벡터라고 하고, F의 원소를 스칼라라고 합니다.^[2]

• 벡터 덧셈 또는 간단히 덧셈이라고 하는 이진 연산은 V의 임의의 두 벡터 v와 w에 일반적으로 v + w로 표기되는 V의 세 번째 벡터를 할당하고 이 두 벡터의 합을 말합니다.

• 스칼라 곱셈이라 불리는 이진 함수는 F의 임의의 스칼라 a와 V의 임의의 벡터 v에 할당되며, 이는 av로 ^{[nb 2]}표시됩니다.

벡터 공간을 가지려면 V에서 모든 u, v와 w, F에서 a와 b에 대해 다음의 8가지 공리가 만족되어야 합니다.^[3]

공리	의미.
벡터 덧셈의 연관성	u + (v + w) = (u + v) + w
벡터 덧셈의 교환성	u + v = v + u
벡터 덧셈의 항등원	모든 v ∈ V에 대해 v + 0 = v인 영벡터라고 하는 원소 0 ∈ V가 존재합니다.
벡터 덧셈의 역요소	모든 v ∈ V에 대하여 v + (-v) = 0인 v의 덧셈 역이라고 하는 원소 -v ∈ V가 존재합니다.
스칼라 곱셈과 필드 곱셈의 호환성	a(bv) = (ab)v [nb 3]
스칼라 곱의 항등원	1v = v, 여기서 1은 F의 곱셈 항등식을 나타냅니다.
벡터 덧셈에 대한 스칼라 곱의 분포성	a(u + v) = au + av
필드 덧셈에 대한 스칼라 곱의 분포성	(a + b)v = av + bv

스칼라장이 실수일 때는 벡터공간을 실수 벡터공간, 스칼라장이 복소수일 때는 벡터공간을 복소 벡터공간이라고 합니다.^[4] 이 두 경우가 가장 일반적이지만 임의의 필드 F에 스칼라가 있는 벡터 공간도 일반적으로 고려됩니다. 이러한 벡터 공간을 F-벡터 공간 또는 F 위의 벡터 공간이라고 합니다.^[5]

벡터 공간에 대한 동등한 정의를 제시할 수 있는데, 이는 훨씬 더 간결하지만 덜 기본적입니다. (벡터 덧셈과 관련된) 첫 번째 네 가지 공리는 벡터 공간은 덧셈 하에서 아벨 군이라고 말합니다. 그리고 (스칼라 곱셈과 관련된) 나머지 네 가지 공리는 이 연산이 필드 F에서 이 그룹의 내형환으로의 환 동형을 정의한다고 말합니다.^[6]

두 벡터의 뺄셈은 다음과 같이 정의할 수 있습니다.

공리의 직접적인 결과는 $모든$ ${\displaystyle s}$ ∈ F ${\$$displaystyles$\in F} 및 v ∈ V에 대해 {\displaystyle \mathbf {v} \in V,}에 대해 다음과 같은 것을 갖습니다.

• ${\displaystyle 0\mathbf {v} =\mathbf {0},}$
• ${\displaystyles\mathbf {0} =\mathbf {0},}$
• ${\displaystyle (-1)\mathbf {v} =-\mathbf {v},}$
• ${\displaystyle sv}$ = ${\$$displaystyle$ s$mathbf$${\displaystyle \{}$$v}$ =\$mathbf {0}은($는${\displaystyle )}$ s = 0 {\displaysty${\displaystyle l}$e s=0} 또${\displaystyle 는}$ v = 0을 의미합니다. {\displaystyle \mathbf ${\displaystyle \{}$v} =\mathbf {0}.}

더 간결하게 말하면, 벡터 공간은 필드 위의 모듈입니다.^[7]

기저, 벡터좌표 및 부분공간

선형결합

F-벡터 공간 V의 원소들의 집합 G가 주어졌을 때, G의 원소들의 일차결합은 다음과 같은 형태의 V의 원소입니다.

$${\displaystyle a_{1}\mathbf {g} _{1}+a_{2}\mathbf {g} _{2}+\cdots +a_{k}\mathbf {g} _{k}$$

where ${\displaystyle a_{1},\ldots ,a_{k}\in F}$ and ${\displaystyle \mathbf {g} _{1},\ldots ,\mathbf {g} _{k}\in G.}$ The scalars ${\displaystyle a_{1},\ldots ,a_{k}}$ are called the coefficients of the linear combination.^[8]

선형독립성

만약 G의 어떤 원소도 G의 다른 원소들의 일차결합으로 쓸 수 없다면, F-벡터 공간 V의 부분집합 G의 원소들은 일차독립이라고 합니다. 마찬가지로, G의 원소들의 두 일차결합이 V의 동일한 원소를 정의한다면, 그들은 일차독립이고, 오직 그들이 같은 계수를 가진 경우에만 그러합니다. 또한 선형 조합이 모든 계수가 0인 경우에만 0 벡터가 되는 경우 선형적으로 독립적입니다.^[9]

선형 부분공간

벡터 공간 V의 선형 부분 공간 또는 벡터 부분 공간 W는 벡터 덧셈 및 스칼라 곱 하에서 닫힌 V의 비어 있지 않은 부분 집합입니다. 즉, W의 두 원소의 합과 W의 원소를 스칼라로 곱한 값이 W에 속합니다.^[10] 이것은 W의 모든 요소의 선형 조합이 W에 속한다는 것을 의미합니다. 선형 부분공간은 유도 덧셈과 스칼라 곱셈을 위한 벡터 공간입니다. 이것은 폐쇄 특성이 벡터 공간의 공리가 만족됨을 의미합니다.^[11]
폐쇄 속성은 선형 부분공간의 모든 교집합이 선형 부분공간임을 의미합니다.^[11]

선형 스팬

벡터 공간 V의 부분 집합 G가 주어지면, G를 포함하는 모든 선형 부분 공간의 교집합이라는 의미에서, 선형 스팬 또는 단순히 G의 스팬은 G를 포함하는 V의 가장 작은 선형 부분 공간입니다. G의 스팬은 또한 G의 원소들의 모든 선형 조합들의 집합입니다.
W가 G의 스팬이면, G는 W를 스팬 또는 생성하고, G는 스팬 집합 또는 생성 집합 W라고 말합니다.^[12]

기초 및 치수

벡터 공간의 부분 집합은 요소가 선형 독립적이고 벡터 공간에 걸쳐 있는 경우 기본입니다.^[13] 모든 벡터 공간에는 적어도 하나의 기저가 있거나, 일반적으로 많이 있습니다(모든 벡터 공간에 기저가 있다는 것은 기초(선형 대수) § 증명 참조). 또한 벡터 공간의 모든 기저는 동일한 카디널리티를 가지며, 이를 벡터 공간의 차원이라고 합니다(벡터 공간의 차원 정리 참조).^[15] 이것은 벡터 공간의 기본 속성이며, 이는 나머지 섹션에 자세히 설명되어 있습니다.

베이스는 특히 차원이 유한한 경우 벡터 공간 연구를 위한 기본 도구입니다. 무한 차원의 경우, 종종 하멜 기지라고 불리는 무한 기지의 존재는 선택의 공리에 달려 있습니다. 따라서 일반적으로 어떤 베이스도 명시적으로 기술할 수 없습니다.^[16] 예를 들어, 실수는 유리수 위에 무한 차원 벡터 공간을 형성하며, 이에 대한 구체적인 근거는 알려져 있지 않습니다.

필드 F 위에 n차원 벡터 공간 V의 기저${\displaystyle }$(${\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {\mathrm{}}_{}}$ ${\displaystyle {}_{}\dots ,}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle (\mathbf {b} _{1},\mathbf {b}$ _${2},\ldots,\mathbf {b}$ _${n})$를 생각해 보자. 기저의 정의는 $모든$ $v$∈ V ${\displaystyle \mathbf$ {$v}$ \in V}이(가) 기록될 수 있음을 의미합니다.

F에 1${\displaystyle {}_{}\dots ,}$ ${\$가 있으면 이 분해가 고유하다는 것을 알 수 있습니다. ${\displaystyle {스칼라}_{}}$ $a{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}\dots ,}$ ${\$를 기준으로 v의 좌표라고 합니다$$. 그것들은 또한 기준으로 v의 분해 계수라고 합니다. 또한 F의 원소 n쌍의$$ 집합 ${\displaystyle {Fn}^{}}$ ${\$ F$^{n}}$은 성분별 덧셈과 스칼라 곱셈을 위한 벡터 공간이며, 그 차원은 n이기 때문에 기본적으로 좌표의 n쌍이 v의 좌표 벡터라고 말합니다.

벡터와 그 좌표 벡터 사이의 일대일 대응은 벡터 덧셈에 벡터 덧셈과 스칼라 곱셈을 스칼라 곱셈에 매핑합니다. 따라서 벡터 공간 동형화로 벡터에 대한 추론과 계산을 그 좌표에 대한 추론과 계산으로 변환할 수 있습니다.^[17] 이 좌표를 행렬로 배열하면 좌표에 대한 이러한 추론과 계산은 행렬에 대한 추론과 계산으로 간결하게 표현될 수 있습니다. 또한 행렬과 관련된 선형 방정식은 선형 방정식 시스템으로 확장될 수 있으며, 반대로 모든 이러한 시스템은 행렬에 대한 선형 방정식으로 압축될 수 있습니다.

벡터 공간 V의 선형 부분 공간 또는 벡터 부분 공간 W는 벡터 덧셈 및 스칼라 곱 하에서 닫힌 V의 비어 있지 않은 부분 집합입니다. 즉, W의 두 원소의 합과 W의 원소를 스칼라로 곱한 값이 W에 속합니다.^[10] 이것은 W의 모든 요소의 선형 조합이 W에 속한다는 것을 의미합니다. 선형 부분공간은 유도 덧셈과 스칼라 곱셈을 위한 벡터 공간입니다. 이것은 폐쇄 특성이 벡터 공간의 공리가 만족됨을 의미합니다. 폐쇄 속성은 선형 부분공간의 모든 교집합이 선형 부분공간임을 의미합니다.^[11]

역사

벡터 공간은 평면 또는 3차원 공간의 좌표 도입을 통해 아핀 기하학에서 비롯됩니다. 1636년경, 프랑스 수학자 르네 데카르트와 피에르 드 페르마는 평면 곡선에 점이 있는 두 변수 방정식의 해를 찾아냄으로써 분석기하학을 확립했습니다.^[18] 좌표를 사용하지 않고 기하학적 해법을 얻기 위해 볼자노는 1804년 벡터의 전신인 점, 선, 평면에 대한 특정 연산을 도입했습니다.^[19] 뫼비우스(Möbius, 1827)는 중심좌표의 개념을 소개했습니다.^[20] 벨라비티스(Bellavitis, 1833)는 등분율이라고 부르는 동일한 길이와 방향을 공유하는 지시된 선분에 등가 관계를 도입했습니다.^[21] 유클리드 벡터는 그 관계의 등가 클래스입니다.^[22]

벡터는 Argand와 Hamilton에 의한 복소수의 제시와 후자에 의한 4등분의 시작으로 재고되었습니다.^[23] 그것들은⁴ R과² R에 있는 원소들인데, 선형 조합을 사용하여 그것들을 처리하는 것은 1867년에 선형 방정식 체계를 정의했던 라구에르로 거슬러 올라갑니다.

1857년 케일리는 선형 지도의 조화와 단순화를 가능하게 하는 행렬 표기법을 도입했습니다. 비슷한 시기에 그라스만은 뫼비우스에 의해 시작된 중심 미적분학을 연구했습니다. 그는 작전을 부여받은 추상적인 물체들의 집합을 상상했습니다.^[24] 그의 작품에는 선형 독립성과 차원의 개념과 스칼라 곱이 존재합니다. 그라스만의 1844년 연구는 벡터 공간의 틀을 뛰어넘을 뿐만 아니라 그의 곱셈에 대한 고찰이 오늘날 대수라고 불리는 것으로 이어졌기 때문입니다. 이탈리아의 수학자 페아노는 1888년에 벡터 공간과 선형 지도에 대한 현대적인 정의를 내렸지만,^[25] 그는 그것들을 "선형 시스템"이라고 불렀습니다.^[26] 페아노의 공리화는 무한 차원의 벡터 공간을 허용했지만, 페아노는 그 이론을 더 이상 발전시키지 않았습니다. 1897년 살바토레 핀슐레는 페아노의 공리를 채택하여 무한차원 벡터 공간 이론에 처음으로 진출했습니다.^[27]

벡터 공간의 중요한 발전은 앙리 르베그(Henri Lebesgue)가 함수 공간을 구축한 덕분입니다. 이것은 이후 1920년경 바나흐와 힐베르트에 의해 공식화되었습니다.^[28] 당시 대수학과 함수해석학의 새로운 분야는 특히 p-적분 함수의 공간과 힐베르트 공간과 같은 핵심 개념들과 상호작용하기 시작했습니다.^[29]

예

평면의 화살표

벡터 공간의 첫 번째 예는 한 고정점에서 시작하는 고정 평면의 화살표로 구성됩니다. 이것은 물리학에서 힘이나 속도를 설명하는 데 사용됩니다.^[30] v와 w와 같은 두 개의 화살표가 주어지면, 이 두 개의 화살표에 걸쳐 있는 평행사변형에는 원점에서 시작하는 대각선 화살표도 하나 포함됩니다. 이 새로운 화살표는 두 화살표의 합이라고 하며 v + w로 표시됩니다. 같은 선에 있는 두 개의 화살표의 특별한 경우, 화살표의 방향성이 같은지에 따라 길이가 합이 되거나 길이의 차이가 되는 이 선의 화살표입니다. 화살표로 할 수 있는 또 다른 연산은 스케일링입니다: 임의의 양의 실수 a가 주어졌을 때, v와 같은 방향을 갖지만 길이에 a를 곱하여 확장되거나 축소된 화살표를 v에 a를 곱한 것을 v의 곱이라고 합니다. av로 표시됩니다. a가 음수이면 av는 대신 반대 방향을 가리키는 화살표로 정의됩니다.^[31]

다음은 몇 가지 예를 보여줍니다: a = 2인 경우, 결과 벡터 aw는 w와 방향이 동일하지만 w(두 번째 이미지)의 두 배 길이로 늘어납니다. 마찬가지로 2w는 합 w + w입니다. 게다가 (-1)v = -v는 v와 반대 방향이고 (두 번째 이미지에서 아래를 가리키는 파란색 벡터) 길이도 같습니다.

순서쌍수

벡터 공간의 두 번째 핵심 예는 실수 x와 y의 쌍에 의해 제공됩니다. 성분 x와 y의 순서는 의미가 크므로 이러한 쌍을 순서쌍이라고도 합니다. 이러한 쌍은 (x, y)로 표시됩니다. 그러한 두 쌍의 합과 숫자가 있는 쌍의 곱은 다음과 같이 정의됩니다.^[32]

위의 첫 번째 예는 화살표가 끝점의 직각좌표 쌍으로 표시되는 경우 이 예로 축소됩니다.

좌표공간

필드 F 위의 벡터 공간의 가장 간단한 예는 필드 F 그 자체이며( 덧셈을 위한 아벨 군이므로 필드가 되기 위한 요구 사항의 일부), 그 덧셈(벡터 덧셈이 됨)과 곱셈(스칼라 곱셈이 됨)이 있습니다. 보다 일반적으로 모든 n-쌍둥이(길이 n의 수열)

F 의 원소 a는_i 일반적으로ⁿ F로 표시되고 좌표 공간이라고 하는 벡터 공간을 형성합니다.^[33] 사례 n = 1은 위에서 언급한 가장 간단한 예이며, 필드 F도 그 자체 위에서 벡터 공간으로 간주됩니다. 사례 F = R과 n = 2 (또는 R)에 대해서는 위 서론에서 논의한 바 있습니다.

복소수 및 기타 필드 확장자

실수 x와 i가 허수 단위인 y의 경우 x + iy의 형태로 쓸 수 있는 복소수 C 집합은 실수 x, y, a, b, c의 경우 (x + iy) + (a + ib) = (x + a) + i(y + b) 및 c ⋅ (x + iy) = (c ⋅ x) + i(c ⋅ y). 벡터 공간의 다양한 공리는 복소수 산술에 대해 동일한 규칙이 성립한다는 사실에서 비롯됩니다. 복소수의 예는 위에서 언급한 실수들의 순서쌍들의 벡터 공간과 본질적으로 같습니다. (즉, 동형이다) 복소수 x + y를 순서쌍 (x,)를 나타내는 것으로 생각하면y) 복소평면에서 우리는 덧셈과 스칼라 곱셈에 대한 규칙이 앞의 예제의 규칙과 정확히 일치한다는 것을 알 수 있습니다.

더 일반적으로, 필드 확장은 특히 대수학과 대수학 수론에서 벡터 공간의 또 다른 예를 제공합니다: 더 작은 필드 E를 포함하는 필드 F는 F의 주어진 곱셈과 덧셈 연산에 의해 E-벡터 공간입니다.^[34] 예를 들어, 복소수는 R 위의 벡터 공간이고, 필드 확장 $Q{\displaystyle \mathbf{}(i}$ ${\displaystyle 5)}$ ${\displaystyle \mathbf {Q}(i{\sqrt {5}})$는 Q 위의 벡터 공간입니다.

함수공간

임의의 고정 집합 ω 에서의 필드 F로의 함수도 덧셈과 스칼라 곱셈을 포인트 단위로 수행하여 벡터 공간을 형성합니다. 즉, 두 함수 f와 g의 합은 다음과 같이 주어진$$ 함수${\displaystyle }$(${\displaystyle f}$+ ${\displaystyle g)}$ ${\displaystyle (f$+ g$)}$입니다.

곱셈도 마찬가지입니다. 이러한 함수 공간은 ω가 R의 실수선 또는 구간 또는 다른 부분 집합인 많은 기하학적 상황에서 발생합니다. 연속성, 적분성 또는 미분성과 같은 위상 및 분석의 많은 개념은 선형성과 관련하여 잘 작동합니다. 그러한 속성을 가진 함수의 합계 및 스칼라 배수는 여전히 해당 속성을 가지고 있습니다.^[35] 따라서 그러한 함수들의 집합은 벡터 공간이며, 벡터 공간의 연구는 함수 분석에 속합니다.

선형방정식

균질한 선형 방정식 체계는 벡터 공간과 밀접하게 연결되어 있습니다.^[36] 예를 들어, 의 솔루션은

임의의 $a$,${\displaystyle$ a,}$$b = $a$ /$$${\displaystyle 2}$, ${\displaystyle$ b = a/2,} 및 c = -5 a / 2$.$ {\displaystyle c =-5a/2.$}$그들은$$ 벡터 공간을 형성합니다: 그러한 삼중의 합과 스칼라 배수는 여전히 세 변수의 동일한 비율을 만족합니다. 따라서 그들 또한 해결책입니다. 행렬을 사용하여 위와 같은 여러 개의 선형 방정식을 하나의 벡터 방정식, 즉

서 A =[ 1 1 4 2 ] {\$displaystyle$ A = {\begin{bmatrix} 1&3&1\\4&2\end{bmatrix}}는 주어진 방정식의 계수를 포함하는 행렬이고, x {\displaystyle \mathbf {x} }는 벡터(a, b$,$ c), {\displaystyle (a, b, c),$}$${\displaystyle x}$ ${\displaystyle A\mathbf {x} }$은 행렬 곱을 나타내고 $0{\displaystyle }$$=$ (${\displaystyle 0,}$0) {\displaystyle \mathbf {0} $=$ (0, 0)}은 영벡터입니다. 비슷한 맥락에서 동차 선형 미분 방정식의 해는 벡터 공간을 형성합니다. 예를들면,

yields ${\displaystyle f(x)=ae^{-x}+bxe^{-x},}$ where ${\displaystyle a}$ and ${\displaystyle b}$ are arbitrary constants, and ${\displaystyle e^{x}}$ is the natural exponential function.

선형 지도 및 행렬

두 벡터 공간의 관계는 선형 지도 또는 선형 변환으로 표현될 수 있습니다. 벡터 공간 구조를 반영하는 함수, 즉 합과 스칼라 곱을 보존하는 함수입니다.

for all ${\displaystyle \mathbf {v} }$ and ${\displaystyle \mathbf {w} }$ in ${\displaystyle V,}$ all ${\displaystyle a}$ in ${\displaystyle F.}$^[37]

동형 사상이란 역맵 g가 존재하는 선형 맵 f : V → W이며, 이는 가능한 두 개의 합성 f : W → W 및 g ∘ f : V → V가 항등식 맵이 되도록 하는 맵입니다. 동등하게 f는 일대일(주입식)과 on(투사식) 모두입니다.^[38] 만약 V와 W 사이에 동형이 존재한다면, 두 공간은 동형이라고 하는데, V에 포함된 모든 항등식은 f를 통해 W의 유사한 항등식으로 수송되고, 그 반대의 항등식은 g를 통해 수송되기 때문에 벡터 공간과 본질적으로 동일합니다.

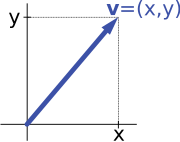
예를 들어, 위의 서론(§ 예 참조)에서 평면 내 화살표와 숫자 벡터 공간의 순서 쌍은 동형입니다. 일부 (고정) 좌표계의 원점에서 출발하는 평면 화살표 v는 오른쪽 이미지와 같이 화살표의 x-성분과 y-성분을 고려하여 순서 쌍으로 표현할 수 있습니다. 반대로 한 쌍(x, y)이 주어지면 오른쪽으로 x가 가고(또는 x가 음수이면 왼쪽으로), y가 위로 가는(아래로, y가 음수이면) 화살표 v를 뒤로 돌립니다.

두 벡터 공간 사이의 선형 맵 V → W는 L(V, W) 또는 𝓛(V, W)로 표시되는 벡터 공간 Hom(V, W)을 형성합니다. V에서 F까지의 선형 지도의 공간을 이중 벡터 공간이라고 하며, 이를 V라고^∗ 합니다.^[40] 주입 자연 지도 V → V를 통해 모든 벡터 공간을 이중으로 삽입할 수 있습니다. 이 지도는 공간이 유한 차원인 경우에만 동형입니다.

일단 V의 기저가 선택되면, V의 모든 요소는 그것들의 선형 조합으로 고유하게 표현되기 때문에, 선형 맵 f: V → W는 기저 벡터의 이미지를 지정함으로써 완전히 결정됩니다. 딤 V = 딤 W인 경우, V와 W의 고정 기저 사이의 1 대 1 대응은 V의 임의의 기저 요소를 W의 대응 기저 요소에 매핑하는 선형 맵을 생성합니다. 그것은 정의상 동형입니다.^[43] 따라서 주어진 필드 위의 두 벡터 공간은 차원이 일치하는 경우 동형이고 그 반대의 경우도 동형입니다. 이것을 표현하는 또 다른 방법은 주어진 필드 위의 벡터 공간이 차원, 즉 단일 숫자에 의해 완전히 (동형까지) 분류된다는 것입니다. 특히, 임의의 n차원 F-벡터 공간 V는 F와ⁿ 동형입니다. 그러나 "동형"이나 선호되는 동형은 없습니다. 동형 φ: F → V는 φ를 통해 F의 표준 기저를 V로 매핑하여 V의 기저를 선택하는 것과 같습니다.

행렬

행렬은 선형 지도를 인코딩하는 데 유용한 개념입니다.^[44] 오른쪽 이미지와 같이 사각형 배열의 스칼라로 표시됩니다. 임의의 m-by-n 행렬 $A{\displaystyle }$ ${\displaystyle A}$는 다음에 의해 F에서ⁿ F로의^m 선형 맵을 생성합니다$$.

$여기서$∑ ${\textstyle \$sum }은 합을 의미하거나$행렬$ A ${\displaystyle$ A}의 행렬 곱을 좌표$벡터$ x${\displaystyle \mathbf$ $\{$x}과 함께 사용합니다.

또한 V와 W의 기저를 선택한 후 이 할당을 통해 임의의 선형 맵 f:V → W를 행렬로 고유하게 표현합니다.

정방 행렬 A의 행렬식 det(A)는 연관된 지도가 동형인지 여부를 알려주는 스칼라입니다: 행렬식이 0이 아닌 것이 충분하고 필요합니다.^[46] 실제 n-by-n 행렬에 해당하는 R의ⁿ 선형 변환은 행렬식이 양수인 경우에만 방향을 보존하는 것입니다.

고유값과 고유벡터

이 경우 벡터 v를 f, f(v) 아래의 이미지와 비교할 수 있기 때문에, 선형 맵 f : V → V인 내형성이 특히 중요합니다. λv = f(v)를 만족하는 0이 아닌 벡터 v는 λ가 스칼라이며 고유값 λ을 갖는 고유 벡터 off라고 합니다. 마찬가지로 v는 차이 f - λ · Id(여기서 Id는 ID 맵 V → V)의 커널 요소입니다. V가 유한 차원인 경우, 이는 다음과 같은 행렬식을 사용하여 표현할 수 있습니다: 고유값 λ을 갖는 f는 다음과 같습니다.

행렬식의 정의를 철자로 적음으로써, 왼쪽에 있는 표현은 f의 특성 다항식이라고 불리는 λ의 다항식 함수라고 볼 수 있습니다. 만약 필드 F가 이 다항식의 0을 포함할 만큼 충분히 크다면 (F = C와 같이 팔지브라로 닫힌 경우에 자동적으로 발생하는) 선형 맵은 적어도 하나의 고유 벡터를 갖습니다. 벡터 공간 V는 고유 벡터로 구성된 기저인 고유 기저를 가질 수도 있고 가지지 않을 수도 있습니다. 이 현상은 요르단의 표준 지도 형식에 의해 지배됩니다.^[49] 특정 고유값 off에 대응하는 모든 고유 벡터의 집합은 문제의 고유값 (및 f)에 대응하는 고유 공간으로 알려진 벡터 공간을 형성합니다.

기본구성

위의 구체적인 예 외에도 주어진 것과 관련된 벡터 공간을 산출하는 다수의 표준 선형 대수적 작도가 있습니다.

부분공간 및 몫공간

덧셈 및 스칼라 곱셈에서 닫힌 벡터$$ 공간 $V{\displaystyle }$ ${\displaystyle V}$의 비어$$ 있지 않은 부분 집합 $W{\displaystyle }$ ${\$$displaystyle$$W$$}$를 V ${\displaystyle$ V$}$의 선형 부분 공간이라고 합니다$.$ $또는{\displaystyle }$ 주변 공간이$$명확하게 벡터 $공간$인 경우 V {\displaystyle V$}$의 부분 공간입니다$.$^{[50][nb 4]} $V{\displaystyle }$ ${\displaystyle V}$의 부분 공간은 자신의 오른쪽에 있는 벡터 공간입니다$$. 벡터들의$$ $주어진{\displaystyle }$ 집합$$S {\$displaystyle S}$를 포함하는 모든 부분공간들의 교집합을 그것의 스팬이라고 하며, 집합 $S{\displaystyle }$ ${\displaystyle S}$를 포함하는 $V{\displaystyle }$ ${\displaystyle$ V$}$의 가장 작은 부분공간입니다$.$ 요소들로 표현하면, 스팬은 $S{\displaystyle }$ ${\displaystyle S}$ 요소의 모든 선형 조합으로 구성된 부분 공간입니다$.$^[51]

차원 1과 2의 선형 부분공간을 각각 선, 평면이라고 합니다. 주변 공간의 기저 중 하나를 제외한 모든 요소를 포함하는 선형 부분공간은 초평면입니다. 유한 차원 $n{\displaystyle }$ ${\displaystyle n}$의 벡터 공간에서$$벡터 초평면은 따라서 차원 $n{\displaystyle }$- ${\displaystyle 1}$ ${\displaystyle n-1}$의 부분 공간입니다$.$

부분 공간에 대응하는 것은 몫 벡터 공간입니다.^[52] $임의$의 부분공간 $W$⊆ V {\$displaystyle$ W$subseteq$ V}이(가) $,$ $몫공간$ V / W${\$$$V$/$$W$}("V${\$$displaystyle$ V} $모듈$로 $W {\$displaystyle W}")는 다음과 같이 정의됩니다. 집합으로 구성됩니다.

여기서 $v{\displaystyle \mathbf{}}$ ${\$은(는) $V{\displaystyle }$ ${\displaystyle$ V$}$의 임의 벡터입니다$.$ ${\displaystyle \mathrm{이러한}}$ 두 요소 $v{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$+ W ${\displaystyle \mathbf {v}$ _${1}+W}$ 및$$ v ${\displaystyle {}_{}}$+ ${\displaystyle W}${\$displaystyle \mathbf {v}$ _${2}+$${\displaystyle W}$$}$의 합은${\displaystyle }$(${\displaystyle v{\mathbf{}}_{}}$ ${\displaystyle {}_{}}$+ ${\displaystyle {\mathrm{}}_{}}$ 2${\displaystyle {}_{}}$+ W ${\displaystyle \left(\mathbf {v} _{1}+\mathbf {v}$ _${2}\right)+$${\displaystyle W}$$\}$이고, 스칼라 곱은 $⋅$${\displaystyle }$(${\displaystyle v}$ + W) $=$${\displaystyle (}$$⋅$ v) + $W${\$displaystyle a\cdot$(\mathbf {v} + W) $=$ (a\cdot \mathbf {v} ) + W}에 의해 주어집니다. The key point in this definition is that ${\displaystyle \mathbf {v} _{1}+W=\mathbf {v} _{2}+W}$if and only if the difference of ${\displaystyle \mathbf {v} _{1}}$ and ${\displaystyle \mathbf {v} _{2}}$ lies in ${\displaystyle W}$.^{[nb 5]} This way, 부분공간 $W{\displaystyle }$ ${\displaystyle W}$에 포함된 몫공간 "잊음" 정보입니다$.$

$선형{\displaystyle 맵}$ ${\displaystyle f}$의 $커널$ ${\displaystyle \ker }$ ⁡ ($f$$)$ {\$displaystyle$\ker$($f)}: V → W {\displaystyle f:$V{\displaystyle }$$\to W}$은(는) W ${\displaystyle W}$의 $0{\displaystyle \mathbf{}}$ ${\$에 매핑된$$ 벡터 $v{\displaystyle \mathbf{}}$ ${\$로 구성됩니다$.$^[53] 커널 및 이미지 ${\displaystyle \mathrm{im}}$⁡(${\displaystyle f}$ ) =${\displaystyle }${${\displaystyle }$f$(v$ ) : v ∈ V} {\displaystyle$$\operatorname {im}(f)=\{f(\mathbf {v}):\mathbf {v} \in V\}는 각각 V {\displaystyle V} 및 W {\displaystyle W}의 하위 공간입니다.

중요한 예는 일부 고정$행렬$ A ${\displaystyle$ A$\}$에 대한 선형 맵 ${\displaystyle x}$ ↦ A x${\displaystyle \mathbf$ {x} $\maps$ to A$\mathbf$ {x}의 커널입니다. $이$ 지도의 커널은 ${\displaystyle A}$ {\displaystyle$$$A$\$mathbf$${x}$ 벡터 $x$ ${\$$displaystyle A\$mathbf ${x}$ =\$mathbf${0$}$의 부분 공간으로$,$ $정확히$는 A$${\$displaystyle$A}에 속하는 동차 선형 방정식 시스템에 대한 해 집합입니다$.$ 이 개념은 선형 미분 방정식으로도 확장됩니다.

${\displaystyle {여기}_{}}$서 계수 ai$${\$displaystyle a_{$i}}는 $x{\displaystyle ,}$ ${\displaystyle$ x$,}$의 함수입니다$$. 해당 지도에서 함수 $f{\displaystyle }$ ${\displaystyle f}$의 도함수는 선형으로 나타납니다$$($예$를 들어$,$ f${\displaystyle {\mathrm{\text{'}}}^{}}$(${\displaystyle {x\mathrm{}}^{}}$ 2 ${\$}($x)^{2}).$ 미분은 선형 절차이므로(즉$,$ (${\displaystyle f}$+ g${\displaystyle {)}^{}}$ = f$'$ +$$$g$' {\displaystyle (f+g)^{\prime } = f^{\prime }+g^{\prime }} 및 (c ⋅ f) = c ⋅ f' {\displaystyle (c\cdot f)^{\prime } = c\cdot f^{\prime }) 상수 c {\displaystyle c}에 대해 이 할당은 선형입니다. 선형 미분 연산자라고 합니다. 특히 미분방정식 $D{\displaystyle (f)}$ = ${\displaystyle 0}$ ${\$displaystyle D(f) = 0}의 해는 (R 또는 C 위에서) 벡터 공간을 형성합니다.

커널과 이미지의 존재는 (고정 필드 $F{\displaystyle }$ ${\displaystyle$ F$}$ 위의$)$ 벡터 공간의 범주가 아벨 범주, 즉 아벨 그룹의 범주와 매우 유사하게 행동하는 수학적 객체와 그들 사이의 구조 보존 맵(카테고리)의 코퍼스라는 진술의 일부입니다.^[55] 이 때문에, 첫 동형 정리(행렬 관련 용어로는 순위-무효 정리라고도 함)와 같은 많은 문장들이 있습니다.

그리고 두 번째와 세 번째 동형 정리는 군에 대한 대응 문장과 매우 유사한 방식으로 공식화되고 증명될 수 있습니다.

직상품 및 직합

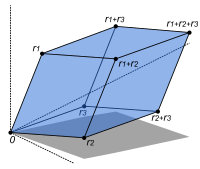
벡터 공간의 직접적인 곱과 벡터 공간의 직접적인 합은 색인화된 벡터 공간 패밀리를 새로운 벡터 공간으로 결합하는 두 가지 방법입니다.

${\displaystyle {직접}_{}}$ 곱 ∏ $I$$$∈ $Vi$$${\displaystyle$V_${i}} 벡터 $공간 Vi {\displaystyle$ V_{i}} 계열의 \$textstyle {\prod_{$i\in I}V_{i}}는$(vi$) i ∈ I,${\displaystyle$ \$left(\mathbf${v} _{i}\right)_{i\in I},$}$ which specify for each index ${\displaystyle i}$ in some index set ${\displaystyle I}$ an element ${\displaystyle \mathbf {v} _{i}}$ of ${\displaystyle V_{i}.}$^[56] Addition and scalar multiplication is performed componentwise. $이$ 구성의 변형은 ∈ I Vi {\$textstyle \bigopplus$_{$i$\in I}V_{i}($동곱이라고$도 $\underset{}{\mathrm{하며}}$∐$I$ ∈ I$Vi$ {\textstyle \coprod _{i\in I}V_{i})이며, 여기서 영이 아닌 벡터가 유한하게 많은 튜플만 허용됩니다. 인덱스 집합 $I{\displaystyle }$ ${\displaystyle I}$가 유한인 경우 두 구성은 일치하지만 일반적으로 다릅니다.

텐서곱

두 벡터 공간 V {\displaystyle V} 및 W {\displaystyle W}의 텐서 곱 ${\displaystyle {}_{}}$ ⊗ F W$,$${\displaystyle$ V$\$otimes W,} 또는 단순히 V ⊗ W, {\displaystyle V\otimes W,}는 선형 맵과 같은 개념을 여러 변수로 확장하는 것을 다루는 다중 선형 대수의 중심 개념 중 하나입니다. ${\displaystyle \mathrm{지도}}$ $g{\displaystyle }$: ${\displaystyle V}$× W → X ${\displaystyle$ g$:$$V\times W\to X}$ from the Cartesian product ${\displaystyle V\times W}$ is called bilinear if ${\displaystyle g}$ is linear in both variables ${\displaystyle \mathbf {v} }$ and ${\displaystyle \mathbf {w} .}$ That is to say, for fixed ${\displaystyle \mathbf {w} }$ the map ${\displaystyle \mathbf{v}\mapsto g(\mathbf{v},}$$displaystyle \mathbf {v} \mapsto g(\mathbf {v},\mathbf {w})}$은(는) 위의 의미에서 선형이며$$ $고정$된 v에 대해서도 마찬가지입니다${\displaystyle .}$ ${\displaystyle \mathbf {v}.}$

텐서 곱은 다음과$$ 같이 쌍선형 맵 $g{\displaystyle ,}$ ${\displaystyle$ g$,}$의 보편적인 수신자인 특정 벡터 공간입니다. 이것은 텐서라고 불리는 유한한 (공식적) 기호의 합으로 구성된 벡터 공간으로 정의됩니다.

규칙에^[57] 의거하여 These rules ensure that the map ${\displaystyle f}$ from the ${\displaystyle V\times W}$ to ${\displaystyle V\otimes W}$ that maps a tuple${\displaystyle (\mathbf {v} ,\mathbf {w} )}$ to ${\displaystyle \mathbf {v} \otimes \mathbf {w} }$ is bilinear. 보편성은 임의의 벡터 공간 $X$ ${\displaystyle X}$와 ${\displaystyle \mathrm{임의}}$의 쌍선형 $맵$ g${\displaystyle :}$ V${\displaystyle }$× W → ${\displaystyle X,}$ ${\displaystyle$ g:$V\times W\to X,}$ there exists a unique map ${\displaystyle u,}$ shown in the diagram with a dotted arrow, whose composition with ${\displaystyle f}$ equals ${\displaystyle g:}$${\displaystyle u(\mathbf {v} \otimes \mathbf {w} )=g(\mathbf {v} ,\mathbf {w} ).$$}$이것은$$^[58] 텐서 곱의 보편적 속성이라고 불리는데, 고급 추상 대수에서 많이 사용되는 방법으로, 이 객체에서 또는 객체로 맵을 지정하여 객체를 간접적으로 정의하는 방법의 한 예입니다.

추가 구조가 있는 벡터 공간

선형 대수학의 관점에서 벡터 공간은 주어진 필드 위의 벡터 공간이 동형까지 차원에 따라 특성화되는 한 완전히 이해됩니다. 그러나 벡터 공간 자체는 일련의 함수가 다른 함수로 수렴하는지 여부와 같은 분석에 중요한 문제를 처리하는 프레임워크를 제공하지 않습니다. 마찬가지로 선형대수학도 무한급수를 다루기에는 적합하지 않습니다. 왜냐하면 덧셈 연산은 유한하게 많은 항만 추가할 수 있기 때문입니다. 따라서 기능 분석의 필요성은 추가적인 구조를 고려할 필요가 있습니다.

벡터$$ 공간은 일부 벡터를 비교할 수 있는 부분 순서 ${\displaystyle \le ,}$ ${\$가 주어질 수 있습니다.^[59] 예를 들어, $n{\displaystyle }$ ${\displaystyle n}$차원$$ 실수 공간 ${\displaystyle {}^{}}$ ${\$의 벡터를 성분별로 비교하여 정렬할$$ 수 있습니다. 순서 벡터 공간, 예를 들어 리에즈 공간은 두 양의 함수의 차이로 함수를 표현하는 능력에 의존하는 르베그 적분의 기본입니다.

여기서 $f{\displaystyle {}^{}}$+ ${\$는 $f{\displaystyle }$ ${\displaystyle$ f$}$의 양의 부분을$$ 나타내고$$ $f{\displaystyle {}^{}}$-$${\$displaystyle$ f$^{-}$의 음의 부분을 나타냅니다.^[60]

정규 벡터 공간과 내부 곱 공간

벡터의 "측정"은 벡터의 길이를 측정하는 기준, 또는 벡터 사이의 각도를 측정하는 내적을 지정함으로써 수행됩니다. 규범과 내부 곱은 ${\displaystyle 각각}$ v $displaystyle \mathbf {v}$ 및 ⟨${\displaystyle }$v, $w$⟩,${\displaystyle \langle \mathbf {v},\$mathbf ${$w} \rangle,}로 표시됩니다. 내부 곱의 데이텀은 연관된 $\sqrt{노름}$ v: =$\sqrt{}$⟨ v, v ⟩을 정의함으로써 벡터의 길이도 정의할 수 있음을 $수반$합니다. ${\textstyle$\mathbf {v} $:$=${\$sqrt {\lang \mathbf {v},\mathbf {v} \rangle }} 이러한 데이터가 부여된 벡터 공간은 각각 정규 벡터 공간과 내부 곱 공간으로 알려져 있습니다.

좌표 공간 ${\displaystyle {Fn}^{}}$ ${\$ 표준 도트 제품을 장착할$$ 수 있습니다.

$R{\displaystyle {\mathbf{}}^{}}$에서 ${\displaystyle \mathbf {R} ^{2}$는 두 벡터$$ $x{\displaystyle \mathbf{}}$ ${\${x$}$와 y$$$,$${\displaystyle \mathbf {y},}$ 사이의 각도에 대한 공통된$$ 개념을 코사인의 법칙에 의해 반영합니다. ${\displaystyle 이}$ 때문에 ⟨ x, $y$ ⟩ = 0 ${\$displaystyle \mathbf {x},\mathbf {y} \rangle = 0}을 만족하는 두 벡터를 직교라고 합니다. 표준 도트 제품의 중요한 변형은 민코프스키 공간에서 사용됩니다. $R{\displaystyle {\mathbf{}}^{}}$ ${\displaystyle {\mathrm{}}^{}}$ ${\$ 로런츠 제품이^[62] 부여됩니다$$. ${\displaystyle 표준}$ 점 제품과 달리 양의 값은 아닙니다. ⟨ x x ⟩ {\$displaystyle \mathbf$ {$x}$\mathbf {x} \rangle } 또한${\displaystyle \mathrm{x}}$=$$($0,$ 0, 0, 1)과 같은${\displaystyle \mathrm{음}}$의 값을 $취합니다$. {\displaystyle \$mathbf {x$} = (0, 0, 0, 1).$}$3개의 공간 차원이 아닌 시간에 해당하는 네 번째 좌표를 선택하면$$ 특수 상대성 이론의 수학적 처리에 유용합니다.

위상벡터공간

수렴 질문은 호환되는 토폴로지를 포함하는 $벡터{\displaystyle }$ 공간 V ${\displaystyle$ V$}$을(를) 고려하여 처리되며, 이는 요소가 서로 가깝다는 것에 대해 이야기할 수 있는 구조입니다.^[63][64] 여기서 호환된다는 것은 덧셈과 스칼라 곱셈이 연속적인 지도여야 한다는 것을 의미합니다. Roughly, if ${\displaystyle \mathbf {x} }$ and ${\displaystyle \mathbf {y} }$ in ${\displaystyle V,}$ and ${\displaystyle a}$ in ${\displaystyle F}$ vary by a bounded amount, then so do ${\displaystyle \mathbf {x} +\mathbf {y} }$ and ${\displaystyle a\mathbf {x} .$$}$스칼라 변화량을 지정하려면 F$$^{[nb 6]} ${\displaystyle F}$ 필드도 $이러한{\displaystyle }$ 맥락에서$$ 토폴로지를 수행해야 합니다. 일반적인 선택은 실수 또는 복소수입니다.

이러한 위상 벡터 공간에서 일련의 벡터를 고려할 수 있습니다. 무한합

는 $V$의 원소들의$$ $수열{\displaystyle {}_{}}$ f ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle {f\mathrm{}}_{}}$ ${\displaystyle {}_{}}$… ${\displaystyle f_{1}, f_{2},\ldots }$의 해당 유한 부분합의 극한을 나타냅니다$.${\$displaystyle$ f_{i$}$는 예를 들어, ${\displaystyle {fi}_{}}$ ${\$}는 어떤 함수 공간 $$에 속하는 (실제 또는 복소) 함수일$$ 수 있습니다${\displaystyle .}$${\displaystyle$ V$,}$ 이 경우$$ 시리즈는 함수 시리즈입니다. 급수의 수렴 모드는 함수 공간에 부과된 토폴로지에 따라 달라집니다. 이러한 경우 점별 수렴과 균일 수렴이 대표적인 예입니다.

어떤 무한급수의 극한이 존재하는 것을 보장하는 방법은 어떤 코시 수열도 극한을 갖는 공간으로 주의를 제한하는 것입니다. 그러한 벡터 공간을 완전하다고 부릅니다. 대략 벡터 공간은 필요한 모든 극한을 포함한다면 완성됩니다. 예를 들어$,{\displaystyle }$ 균일 수렴의 토폴로지를$$갖춘 단위 구간 [0, 1$],${\displaystyle [$0$$,$ $1]$의 다항식들의 벡터 공간은 [${\displaystyle 0,}$${\displaystyle }$$]$의 어떤 연속 함수도 다항식들의 시퀀스에 의해 균일하게 근사될$$ 수 있기 때문에 완전하지 않습니다. 위어스트라스 근사 정리에 의해서.^[65] 대조적으로$,{\displaystyle }$ 위상이 동일한$$ [${\displaystyle 0,}$1$]$ {\$displaystyle [0,$ 1$]}$의 모든 연속 함수의 공간은 완성됩니다.^[66] norm은 v ${\$ 벡터 ${\displaystyle {}_{}}$가 $v{\displaystyle \mathbf{}}$ ${\$로 수렴하는$$ 것을 정의함으로써 토폴로지를 생성합니다. 이는 다음과 같은 경우에만 가능합니다.

바나흐와 힐베르트 공간은 각각 정규와 내적에 의해 위상이 주어진 완전한 위상 벡터 공간입니다. 유한 차원 위상 벡터 공간에 대한 모든 규범은 동일한 수렴 개념을 생성하기 때문에 함수 분석의 핵심 부분인 그들의 연구는 무한 차원 벡터 공간에 초점을 맞추고 있습니다.^[67] 오른쪽 이미지는 $R$ $2:{\$$displaystyle 1}$ -norm 및$$∞ {\$displaystyle$\infty} ${\displaystyle {}^{}}$의 동등성을 보여줍니다. ${\displaystyle \mathbf${R} ^{2}: 단위 "볼"이 서로 둘러싸기 때문에 시퀀스가 다른 norm에서 0인 경우에만 한 norm에서 0으로 수렴됩니다. 그러나 무한 차원의 경우 일반적으로 동일하지 않은 위상이 존재할 것이며, 이는 추가 데이터가 없는 벡터 공간보다 위상 벡터 공간에 대한 연구를 풍부하게 만듭니다.

개념적 관점에서 위상 벡터 공간과 관련된 모든 개념은 위상과 일치해야 합니다. 예를 들어, 모든 선형 맵(함수라고도 함) $V$ → ${\displaystyle W,}$ {\$displaystyle$ $V\to$ W$,}$개의 $위상$ 벡터 공간 사이의 맵은 연속적이어야 합니다. 특히 ($위상$) 듀얼 공간 $V$ ∗ {\$displaystyle$ V^{*}}는 연속 $함수$ ${\displaystyle V}$ → R ${\displaystyle$V\ $to \mathbf$ {R}($또는$C ${\displaystyle \mathbf$ {C}})로 구성됩니다. 기본적인 한-바나흐 정리는 연속 함수에 의해 적절한 위상 벡터 공간의 부분 공간을 분리하는 것에 관한 것입니다.^[69]

바나흐 공백

스테판 바나흐가 도입한 바나흐 공간은 완전한 정규 벡터 공간입니다.^[70]

첫 번째 예는 실수 $엔트리$ ${\displaystyle x_{}}$ = (${\displaystyle x_{}}$1,$x$2$,$…, x n, …) {\displaystyle \mathbf {x} =\left(x_{1}, x_{2},\ldots,x_{n}를 가진 무한 벡터로 구성된 벡터 공간$$ℓ p ${\displaystyle \ell$ ^{p}}입니다.$p$가$${\$displaystyle$p} -norm$1$≤ p${\displaystyle }$≤$$$∞$) ${\displaystyle(1\leq$ p$\$leq \infty)}인$\dots \right)}$

무한 차원 공간$$ℓ p ${\displaystyle \ell$ ^{p}}의 위상은$서로$ 다른 $p$에 대해 동일하지 않습니다. ${\displaystyle$ p.} ${\displaystyle {}_{}}$를 들어, 벡터 x ${\displaystyle n^{}}$= (${\displaystyle {}^{}}$n, 2 - n, $…, 2$ - n, 0, 0, …), {\displaystyle \mathbf {x} _{n} =\left(2^{-n}, 2^{-n},\ldots, 2^{-n}, 0,0,0,$\ldots \right),}$ in which the first ${\displaystyle 2^{n}}$ components are ${\displaystyle 2^{-n}}$ and the following ones are ${\displaystyle 0,}$ converges to the zero vector for ${\displaystyle p=\infty ,}$ but does not for ${\displaystyle p=1:}$

그렇지만

실수의 시퀀스보다 일반적으로 함수 $f{\displaystyle :}$ ω → R {\$displaystyle$ f:$\Omega \to \mathbb {R} }$에는 위의 합을 르베그 적분으로 대체하는 노름이 부여됩니다$$.

The space of integrable functions on a given domain ${\displaystyle \Omega }$ (for example an interval) satisfying ${\displaystyle \ f\ _{p}<\infty ,}$ and equipped with this norm are called Lebesgue spaces, denoted ${\displaystyle L^{\;\!p}(\Omega ).}$^{[nb 7]}

이 공간들은 완성되었습니다.^[71] (대신 리만 적분을 사용하면 공간이 완전하지 않기 때문에 르베슈의 적분 이론을 정당화하는 것으로 볼 수 있습니다.)^{[nb 8]} 구체적으로, 은 ‖fn ‖ p < ∞, {\$displaystyle \$ f_${$$n$$}\_{p$}<\infty,} 조건을 만족시키는 르베그 적분 가능 $함수$ ${\displaystyle f_{}}$ 1${\displaystyle {}_{}}$ ${\displaystyle f_{}}$2${\displaystyle ,}$ …\$f$ n${\displaystyle ,}$ …$${\$displaystyle f_{n},\displaystyle$\f_${$n}\_{p$}<\$infty,}

벡터 공간 ${\displaystyle {Lp}^{}}$ω) {\displaystyle $L^{\;\!p}(\$Omega )}에 속하는 함수 $f{\displaystyle (x)}$ ${\displaystyle$ $f$$(x)}$가 존재하여 다음과 같이 수행됩니다.

유계 조건을 함수뿐만 아니라 도함수에도 부과하면 소볼레프 공간으로 이어집니다.^[72]

힐베르트 공간

완전한 내부 곱 공간은 데이비드 힐버트를 기리기 위해 힐버트 공간으로 알려져 있습니다.^[73] 힐베르트 공간 ${\displaystyle {L2}^{}}$ω), ${\displaystyle$ L^{2$}(\$Omega),} 내부 곱은 다음과 같습니다.

여기서 $g$ ¯ ${\displaystyle$ {\$overline {g$(x)}}은${\displaystyle }$g$(x$)의 복소${\displaystyle }켤레$를 나타내고, ${\displaystyle$ g(x$)}$는 키 케이스입니다.

정의에 따라 힐베르트 공간에서 모든 코시 수열은 극한으로 수렴합니다. 반대로, 주어진 극한 함수에 근사하는 바람직한 성질을$$ 가진 ${\displaystyle {함수}_{}}$ f$${\$displaystyle f_{n}}$의 시퀀스를 찾는 것도 마찬가지로 중요합니다. 초기 분석에서는 테일러 근사를 가장하여 다항식에 의한$$ 미분 가능 함수 $f{\displaystyle }$ ${\displaystyle f}$의 근사를 확립했습니다.^[75] 스톤-위어스트라스 정리에 의해${\displaystyle }$[${\displaystyle a,}$ ${\displaystyle b]}$ ${\displaystyle [a,$ b$]}$의 모든 연속 함수는 다항식으로 원하는 만큼 근사할 수 있습니다$$.^[76] 삼각함수에 의한 이와 유사한 근사 기법은 흔히 푸리에 팽창이라고 불리며, 공학에서 많이 적용됩니다. 보다 일반적이고 보다 개념적으로, 이 정리는 "기본 함수"가 무엇인지 또는 추상적인 힐베르트 공간에서 어떤 기본 벡터가 $힐베르트{\displaystyle }$ 공간${\displaystyle }$H$,$ {\$displaystyle$ H$,}$을 생성하기에 충분한지에 대한 간단한 설명을 제공합니다. 이는 스팬의 폐쇄(즉, 유한 선형 조합 및 한계)가$$ 전체 공간이라는 의미에서입니다. 이러한 함수의 $집합$을${\displaystyle }$H의 기저라고$$하며, {\$displaystyle$ H$,}$ 그$$ 카디널리티를 힐베르트 공간 차원이라고 합니다.^{[nb 10]} 이 정리는 근사 목적을 위해 충분한 적절한 기저 함수를 나타낼 뿐만 아니라, Gram-Schmidt 프로세스와 함께 직교 벡터의 기초를 구성할 수 있습니다.^[77] 이러한 직교 기저는 유한 차원 유클리드 공간에서 좌표 축의 힐베르트 공간 일반화입니다.

다양한 미분방정식의 해는 힐베르트 공간으로 해석될 수 있습니다. 예를 들어, 물리학과 공학에서 매우 많은 분야가 이러한 방정식으로 이어지고 특정 물리적 특성을 가진 솔루션이 종종 기저 함수로 사용되며 종종 직교합니다.^[78] 물리학의 한 예로, 양자역학의 시간 의존적 슈뢰딩거 방정식은 시간에 따른 물리적 성질의 변화를 편미분 방정식으로 설명하며, 그 해를 파동함수라고 합니다.^[79] 에너지 또는 운동량과 같은 물리적 특성에 대한 정칙 값은 특정 (선형) 미분 연산자의 고유 값에 해당하며 관련 파동 함수를 고유 상태라고 합니다. 스펙트럼 정리는 이러한 고유 함수와 고유 값의 관점에서 함수에 작용하는 선형 콤팩트 연산자를 분해합니다.^[80]

밭위의 대수

일반 벡터 공간은 벡터 간의 곱셈을 갖지 않습니다. 두 벡터의 곱을 정의하는 추가 이중선형 연산자를 갖춘 벡터 공간은 필드 위의 대수(또는 필드 F가 지정된 경우 F-대수)입니다.^[81]

예를 들어, 모든 다항식 $p{\displaystyle (t)}$ ${\displaystyle$ p$(t)}$의 집합은 다항식 고리로 알려진 대수를 형성합니다$$. 두 다항식의 합이 다항식이므로 벡터 공간을 형성하고, 두 다항식의 곱이 다시 다항식이므로 대수를 형성합니다. 다항식의 고리(여러 변수에서)와 그 몫들은 대수 기하학적 대상의 함수의 고리이기 때문에 대수 기하학의 기초를 형성합니다.^[82]

또 다른 중요한 예는 Lie algebra로, 이들은 교환적이지도 않고 연관적이지도 않지만, 그렇게 하지 못하는 것은 제약 조건에 의해 제한됩니다$([$ y] {\$displaystyle [x,$ y$]$는 $x{\displaystyle }$ ${\displaystyle$ x$}$와 y ${\displaystyle y}$의 곱을 나타냅니다$$).$$

• ${\displaystyle [}$ ${\displaystyle x,}$ ${\displaystyle y}$] =${\displaystyle }$-$$[ y, x ] {\displaystyle [x${\displaystyle ,}$y] = -[y,x]} (Anticomutivity), 그리고
• $displaystyle [x,[y,z]]$$+[y,[z,x]]+[z,[x,y]]=0}$ (Jacobi identity).^[83]

$$를 들어$,$ [${\displaystyle x,}$ y] = x$y$ - ${\displaystyle y}$$$x, {\$displaystyle$ [x, y${\displaystyle ]}$ = x$$y - y x, {\displaystyle [x, y] xy xy-yx,} 두 행렬의 교환기와 교차 곱이 부여된 R 3, {\displaystyle \mathbf {R} ^{3}}의 벡터 공간이 있습니다.

텐서 대수 ${\displaystyle T}$ ⁡ (V) ${\displaystyle \operatorname {$T} (V)}은 대수를 얻기 위해 임의의 $공간$ V ${\displaystyle$ V}에 곱을 추가하는 형식적인 방법입니다. 벡터 공간으로서, 그것은 단순 텐서라고 불리는 기호들에 의해 걸쳐져 있습니다.

$$서$${\$displaystyle$ n$}$의 정도가 달라집니다$$. 곱셈은 그러한 기호를 연결하고, 덧셈 하에서 분배 법칙을 부과하고, 스칼라 곱이 텐서 곱 ⊗과 통근하도록 요구함으로써 주어지는데, 이는 텐서 곱에 대한 위 섹션에서 소개한 두 벡터 공간의 텐서 곱과 매우 동일한 방식입니다. 일반적으로 $v$ ${\displaystyle {}_{}}$ ⊗ v $2$${\displaystyle \mathbf${v}_{1}\otimes \mathbf {v}_{2}와 v 2 ⊗ v 1 사이에는 아무런 관계가 없습니다. {\displaystyle \mathbf {v}_{2}\otimes \mathbf {v}_{1}} 그러한 두 요소가 동일하도록 강제하면 대칭 대수가 됩니다. $강제$ v ${\displaystyle {}_{}}$ ⊗ v$2$= - v 2 ⊗ v 1 {\displaystyle \mathbf {v}_{1}\otimes \mathbf {v}_{2}=-\mathbf {v}\otimes \mathbf {v}_{1}는 외부 대수를 산출합니다.

관련 구조물

벡터 다발

벡터 다발은 위상 공간 X에 의해 연속적으로 매개변수화되는 벡터 공간들의 계열입니다.^[86] 더 정확하게 말하면, X 위의 벡터 다발은 연속적인 지도를 갖춘 위상 공간 E입니다.

따라서 X의 모든 x에 대하여, 섬유 π(x)는 벡터 공간입니다. 대소문자 딤 V = 1을 선다발이라고 합니다. 임의의 벡터 공간 V에 대하여, 사영 X × V → X는 곱 X × V를 "trivial" 벡터 다발로 만듭니다. X 위의 벡터 다발은 국소적으로 X와 일부 (고정된) 벡터 공간 V의 곱이어야 합니다. X의 모든 x에 대하여, π(U)에 대한 π의 제한이 자명한 다발 U × V → U와 동형이 되도록 x의 근방 U가 존재합니다. 그들의 국소적으로 사소한 특성에도 불구하고, 벡터 다발은 (기본 공간 X의 모양에 따라) 큰 부분에서 "뒤틀림"될 수 있습니다(즉, 다발은 (전체적으로) 사소 다발 X × V일 필요가 없습니다). 예를 들어, 뫼비우스 띠는 (실선과 열린 구간을 식별함으로써) 원 S¹ 위의 선다발로 볼 수 있습니다. 그러나 실린더¹ S × R과는 다릅니다. 후자는 방향을 잡을 수 있는 반면 전자는 방향을 잡을 수 없기 때문입니다.^[87]

특정 벡터 다발의 속성은 기본 위상 공간에 대한 정보를 제공합니다. 예를 들어, 접선 다발은 미분 가능한 다양체의 점으로 매개변수화된 접선 공간의 집합으로 구성됩니다. S¹ 위에 0이 아닌 전역¹ 벡터장이 존재하기 때문에, 원 S의¹ 접다발은 S × R과 전역적으로 동형입니다.^{[nb 12]} 대조적으로, 털이 많은 공 정리에 의해, 0이 아닌 모든 곳에 있는 2-구 S에는² (접합) 벡터장이 없습니다.^[88] K-이론은 일부 위상 공간에 대한 모든 벡터 다발의 동형 클래스를 연구합니다.^[89] 위상 및 기하학적 통찰력을 심화시킬 뿐만 아니라 유한 차원 실수 분할 대수의 분류: R, C, 4분위수 H 및 8분위수 O와 같은 순수한 대수적 결과를 가져옵니다.

미분 가능한 다양체의 코탄젠트 다발은 다양체의 모든 점에서 접공간의 이중인 코탄젠트 공간으로 구성됩니다. 해당 번들의 섹션은 차등 단일 형태로 알려져 있습니다.

모듈

모듈은 필드에 대한 벡터 공간을 링하는 것입니다. 필드 F 대신 링 R에 적용되는 동일한 공리, 수율 모듈입니다.^[90] 모듈의 이론은 벡터 공간의 이론에 비해 곱셈적 역을 갖지 않는 링 요소의 존재로 인해 복잡합니다. 예를 들어, 모듈에는 Z-모듈(즉, 아벨 군) Z/2Z가 보여주는 것처럼 베이스가 필요하지 않습니다. 모든 벡터 공간을 포함하는 모듈을 자유 모듈이라고 합니다. 그럼에도 불구하고 벡터 공간은 필드인 링 위의 모듈로 간결하게 정의될 수 있으며 요소는 벡터라고 불립니다. 일부 저자는 벡터 공간이라는 용어를 분할 링 위의 모듈을 의미하는 데 사용합니다.^[91] 스펙트럼을 통한 교환 고리의 대수학적 해석을 통해 벡터 번들에 대한 대수적 대응인 국부적 자유 모듈과 같은 개념을 개발할 수 있습니다.

아핀 공간과 사영 공간

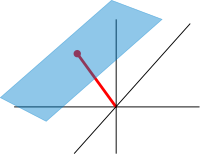
대략 아핀 공간은 기원이 지정되지 않은 벡터 공간입니다.^[92] 좀 더 정확하게 말하면, 아핀 공간은 자유로운 추이 벡터 공간 작용을 갖는 집합입니다. 특히 벡터 공간은 지도에 의해 그 자체로 아핀 공간입니다.

W가 벡터 공간이라면 아핀 부분공간은 선형 부분공간 V를 고정 벡터 x ∈ W로 변환하여 얻은 W의 부분집합입니다. 이 공간은 x + V로 표시되며 (W에서 V의 공집합) v ∈ V에 대한 x + v 형태의 모든 벡터로 구성됩니다. 중요한 예는 비균질 일차방정식의 해의 공간입니다. 위 절에서 논의한 동질적인 경우를 선형 방정식에 일반화하는 것은 이 $방정식$에서 b = ${\$displaystyle \mathbf {b$}$ =\mathbf {0}을(를) 설정하면 알 수 있습니다. 해의 공간은 아핀 부분공간 x + V이며, 여기서 x는 방정식의 특정 해이고, V는 동차 방정식의 해의 공간(A의 널 공간)입니다.

사영 공간은 고정된 유한 차원 벡터 공간 V의 1차원 부분 공간의 집합으로, 무한대에서 교차하는 평행선의 개념을 공식화하는 데 사용될 수 있습니다.^[94] 잔디 매니안과 플래그 매니폴드는 각각 고정 차원 k의 선형 부분 공간과 부분 공간의 플래그를 매개 변수화하여 이를 일반화합니다.

메모들

인용

참고문헌

대수학

분석.

역사참고문헌

추가참조사항

외부 링크

• "Vector space", Encyclopedia of Mathematics, EMS Press, 2001 [1994]