선형 지도
Linear map수학에서, 더 구체적으로 선형 대수학에서 선형 맵(선형 매핑, 선형 변환, 벡터 공간 동형화 또는 일부 맥락에서 선형 함수라고도 함)은 벡터 덧셈과 스칼라 곱셈의 연산을 보존하는 두 벡터 공간 사이의 매핑 → W 입니다.동일한 이름과 동일한 정의는 링 위의 모듈의 일반적인 경우에도 사용됩니다. 모듈 동형화를 참조하십시오.
선형 맵이 비투영이면 선형 동형이라고 합니다. = V = 인 경우 선형 맵을 선형 내동형이라고 합니다때때로 선형 연산자라는 용어는 이 경우를 나타내지만 선형 연산자라는 용어는 다른 규약에서 다른 의미를 가질 수 있습니다. 예를 들어 및 이(꼭 = W V = 인 것은 아님) }을(를) 강조하는 데 사용할 수 있습니다.은(는) 함수 공간으로 함수 분석의 일반적인 규칙입니다.[2]선형 함수라는 용어는 선형 맵과 동일한 의미를 갖는 경우가 있는 반면 분석에서는 그렇지 않습니다.
V에서 W까지의 선형 맵은 항상 V의 원점을 W의 원점에 매핑합니다. 또한 V의 선형 부분공간을 W의 선형 부분공간에 매핑합니다.[3] 예를 들어 V의 원점을 통과하는 평면을 W의 원점을 통과하는 평면, W의 원점을 통과하는 선을 통과하는 평면, 또는 W의 원점만을 통과하는 평면에 매핑합니다. 선형 맵은 종종 다음과 같을 수 있습니다.행렬로 표현되며, 간단한 예로는 회전 및 반사 선형 변환이 있습니다.
범주 이론의 언어에서 선형 지도는 벡터 공간의 형태입니다.
정의 및 첫번째 결과
및 W 을(를) 동일한 K 의 벡터 공백이라 하자 함수 : → W f :는의두 u v V {{v \in V} 의 스칼라c K {\ c\in K에 대해 다음 두 조건을 만족하는 경우 선형 맵이라고 합니다.
따라서 선형 맵은 작업 보존이라고 합니다.즉, 선형 맵이 덧셈 및 스칼라 곱셈 연산 전에 적용되는지(위의 예제의 오른쪽) 또는 후에 적용되는지(예의 왼쪽)는 중요하지 않습니다.
임의의 벡터 에 대하여+로 표시된 덧셈 연산의 에 의해,∈ V 및 스칼라 ∈ K은 다음과 같은 동등함을 갖습니다.
공간 및 W 의 0요소를 각각 \ 및 로 표시하면 ()= 됩니다 {\f(\_{V}) =\ _{가 됩니다.차수 1의 동질성에 대한 방정식에서 c이고 V라고 하자:
가 인 선형 맵 → K 을(를) 일차 벡터 공간이라고 합니다.
이러한 문장은 수정 없이 링 위의 임의의 왼쪽 {\{}에 일반화되고 스칼라 곱셈을 뒤집을 때 임의의 오른쪽 모듈에 일반화됩니다.
예
- 선형 맵에 이름을 부여하는 전형적인 예는 f: → : ↦ :\ \ : 이며 이 중 그래프는 원점을 통과하는 선입니다.
- 보다 일반적으로, 벡터 공간의 원점에 중심을 둔 임의의 호모토티 ↦ v 는 선형 맵(여기서 c는 스칼라)입니다.
- 벡터 공간 사이의 영 맵 x ↦ to 는) 선형입니다.
- 모듈의 아이덴티티 맵은 선형 연산자입니다.
- 실수의 경우 지도 ↦ x x는 선형이 아닙니다.
- 실수의 경우 지도 ↦ + 은(는) 선형이 아니지만 아핀 변환입니다.
- 가 × {\ m n 실제 행렬인 경우, {\ 는 열 ∈ \ \ \in \displaystyle A\mathbf x} \ \m\ {x}^{. 반대로, 유한 차원 벡터 공간 사이의 선형 맵은 이런 식으로 나타낼 수 있습니다. 아래의 행렬을 참조하십시오.
- f : → W 는 ( 0 f) 0 가 선형 맵이 되도록 실제 정규 공간 사이의 등각입니다.이 결과는 복잡한 정규 공간의 경우에 반드시 성립하지는 않습니다.[8]
- 미분은 미분 가능한 모든 함수의 공간에서 모든 함수의 공간으로의 선형 맵을 정의합니다.또한 모든 매끄러운 함수의 공간에 선형 연산자를 정의합니다(선형 연산자는 선형 내형(linear endomorphism), 즉 도메인과 코드 도메인이 동일한 선형 맵).실제로.
- 어떤 구간 I에 대한 정적분은 I의 모든 실수 값 적분 가능 함수의 공간에서 까지의 선형 맵입니다 실제로,
- 적분 시작점이 고정된 부정적분(또는 원시함수)은 의 모든 실수 값 적분 가능 함수의 공간에서 의 모든 실수 값 미분 가능 함수의 공간으로의 선형 맵을 정의합니다 시작점이 고정되지 않으면,상수 함수의 선형 공간에 의해 미분 가능한 함수의 몫 공간에 대한 항미분 지도.
- 와 가 각각의 차원 m과 n의 필드 F 위의 유한 차원 벡터 공간이라면 선형 맵 를 매핑하는 함수: → W 에 설명된 방식의 V\ × m 행렬 행렬(아래)은 선형 맵이며, 선형 동형화도 있습니다.
- 랜덤 변수(사실은 함수이며 벡터 공간의 요소)의 기댓값은 선형이며, 랜덤 변수 및 의 경우 [+ Y ]= [ X]+ E[ ] + Y] = E X+ 및 a ]이지만 랜덤 변수의 분산은 선형이 아닙니다
-
: → f f( =( {\)}는 선형 맵입니다.이 함수는 벡터의 성분을 인자 2 축척합니다
-
f( ) = y) )= (2 x은(는) 덧셈입니다:벡터가 먼저 추가된 다음 매핑된 것인지 또는 매핑된 후 최종적으로 추가된 것인지 는 중요하지 않습니다. f (+ b) = f( )+ f( ) f ) = f ) + f )
-
함수 ( y) = y) )= (2 x은(는) 동차입니다:벡터가 먼저 스케일링된 후, 매핑된 후, 또는 먼저 맵핑된 후 스케일링된 후, (λ a) =λ ( ) f lambda ) =\lambda f )
선형 확장
종종 선형 맵은 벡터 공간의 부분 집합에 정의된 다음 도메인의 선형 스팬까지 선형으로 확장하여 구성됩니다. 및 Y 를 벡터 공백이고 f: → 은(는) 일부 집합 X에 정의된함수입니다 {\ S\ 그런 다음 를 로 선형 확장하는 displaystyle X,{\ 하는 경우)는 displaystyle F를 하는 X Y {\ F입니다 ∈ 이고 코드 도메인에서 값을 부분 집합 이( X {\ X의 벡터 부분 공간일 때 에 ( - 값) 선형 확장 f X}이(가) 존재하는 것은 F: S Y 은(는) 선형 맵입니다.[9]특히 에 에 걸쳐 있는 선형 확장이 X 에 선형 확장이 있습니다
맵 : → Y f:을(를) 선형 맵 로 확장할 수 있습니다 {\ F S}, n> 0 {\n인 경우에만 정수, c n{\은 스칼라, {\ 는 0 1 + + , 필수적으로 1 ( 1) ++ ( 0).선형 확장이인경우 : Y {\displaystyle 이(가) 있으면 선형 확장 F: 이(가) 고유합니다.
예를 들어, = R X =\2이고 Y = Y =\인 경우, 할당( ) → - 1{\및 ( = {\ 1 2은(는) 벡터 의 선형 독립 집합에서 선형으로 확장될 수 있습니다 ={( 0),( ) S:→\{(), {( 0), 1 = R . ), )\}=\ 고유한 선형 확장자 F는 y = + 1 R ,)= + 에 보내는 맵입니다.
실수 또는 복소 벡터 공간 의 벡터 부분 공간 X {\에 정의된 모든 (스칼라 의) 선형 displaystyle f는 X 에 대한 선형 확장을 X 실제로, 한-바나흐 지배 확장 정리는 이 선형 f{\가 어떤 주어진 sem에 의해 지배될 때조차 보장합니다.inorm : → }(( m ≤ ( ) 도메인의 m m에 대해 {\displaystyle f \ p(m)}이(가 유지되는 경우 에 대한 선형 확장이 합니다.
행렬
및 W 이(가) 유한 차원 벡터 공간이고 각 벡터 공간에 대해 기저가 정의되어 있으면 에서 W 까지의 모든 선형 맵을 행렬로 나타낼 수 있습니다.[11]이것은 구체적인 계산이 가능하기 때문에 유용합니다.행렬은 선형 맵의 예를 산출합니다. 만약 가 실제 × n 행렬이라면, ( = f = 는 선형 R → {\^{ \^{유클리드 공간 참조).
…,v 를 의 기본이라고 하자. 그러면 모든벡터 ∈ V 는 R 필드의 계수 에 의해 고유하게 결정됩니다: \ :
f : → W 은(는) 선형 맵입니다.
이것은 함수 가 벡터 f (v ( ){\에 의해 전적으로 결정된다는 것을 의미합니다 이제{ w …,w {w} 1 {w} _가 W {\displaystyle 의 기초가 된다고 하자.그러면 각 벡터 ( f를 다음과 같이 나타낼 수 있습니다.
따라서 함수 는 전적으로 의 값에 의해 결정됩니다 만약 이 을 × n m M 에 넣으면 V의 어떤 에 대해서도 {\의 벡터 출력을 계산하는 데 편리하게 사용할 수 있습니다 M 을 의 열 j 는 벡터입니다.
선형 변환의 행렬은 시각적으로 나타낼 수 있습니다.
- 에 대한 T 행렬 : A {\
- 에 대한 행렬 :
- 에서 으)로의 변환 행렬 :
- 에서 B로의 : P -1 P
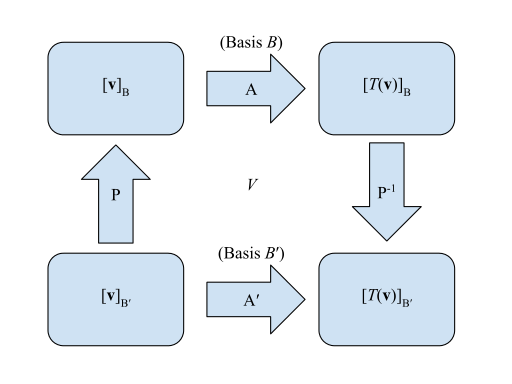
왼쪽 하단 모서리 [ 로 시작하는 것. 오른쪽 하단 모서리 찾기[ ] [하나는 왼쪽 입니다. 즉, '[ ]B [ ()] 동치법은 [ 같은 점에서 시계 방향으로 가는 "길어진" 방법입니다.은(는) - 1 또는 - 1 [ [ P 함께 왼쪽 입니다.
2차원의 예제
2차원 공간에서 선형2 맵 R은 2×2 행렬로 설명됩니다.다음은 몇 가지 예입니다.
- 윤번의
- 시계 반대 방향으로 90도만큼:
- 시계 반대 방향으로 θ 각도만큼:
- 시계 반대 방향으로 90도만큼:
- 반사
- x축을 통해:
- y축을 통해:
- 원점과 θ 각도를 이루는 선을 통해:
- x축을 통해:
- 모든 방향에서 2씩 축척:
- 수평 전단 매핑:
- 각도 θ로 y 축을 스큐합니다.
- 스퀴즈 매핑:
- y 축에 투영:
선형 맵이 회전, 반사 및/또는 균일한 축척으로만 구성되어 있고 불균일한 축척, 전단, 스큐, 스퀴즈 또는 투영으로 구성되어 있지 않다면 선형 맵은 등각 맵의 속성을 가지므로 등각 선형 변환입니다.
선형 맵의 벡터 공간
선형 맵의 구성은 선형: : → W f: 및 Z 는 선형이며, 이들의 합성 f : f: 이로부터, K-선형 맵과 함께, 주어진 필드 K에 대한 모든 벡터 공간의 클래스가 형태소로서 범주를 형성함을 알 수 있습니다.
선형 맵의 역은 정의될 때 다시 선형 맵입니다.
인 경우 →W {\f_}: 및 W 는 선형이므로, 점별 합 1 + 2{\ + 도 입니다는 (f + )( ) f ( x)+ 2 (x) + (\ + 로 정의됩니다
f : → W 는 선형이고 α 는 접지 필드 의 요소입니다 그러면(f) ( ) (x){\ f) (\ ) \로 정의되는맵 f도 선형입니다
따라서 에서 W W까지의 선형 맵의 집합 L ( {\ ( 는 K {\ K 위에 벡터 공간을 형성하며 (V {\{Hom ()}로 표시하기도 합니다 =W {\ V=의 경우,이 벡터 공간은 는 두 선형 맵의 구성이 다시 선형 맵이고, 맵의 구성은 항상 연관성이 있기 때문에 맵의 구성 하에서 연관 대수입니다.이 건에 대해서는 아래에서 더 자세히 설명합니다.
다시 말하면, 기저가 선택되었다면 선형 맵의 구성은 행렬의 곱에 해당하고, 선형 맵의 덧셈은 행렬의 덧셈에 해당하며, 선형 맵과 스칼라의 곱셈은 스칼라의 행렬의 곱에 해당합니다.
내상형법과 자기형
선형 변환 : → V f:는 의 내형이다 위에서 정의된 바와 같이 덧셈, 합성 및 스칼라 곱셈과 함께 모든 이러한 내형 의 집합 은 특히 링) 필드 위에 항등식 요소와 연관 대수를 형성합니다.이 대수의 곱셈 항등식 요소는 항등식 → V : 입니다
동형인 {\ V의 내형을 의 자동형이라고 합니다두 개의 오토모피즘의 구성은 다시 오토모피즘이며, 의 모든 오토모피즘의 집합은 그룹을 형성하며, 의 오토모피즘 그룹은 또는 로 표시됩니다 오토모피즘은 정확히 이러한 내형이기 때문에구성 하에 역수를 갖는 isms, 은 고리에 있는 단위 그룹입니다
에 유한 n 이(가) 있으면 )}은는 의 항목을 가진 ×n {\n} 행렬의 연관 대수와 입니다 V {\ V의 오토모피즘 그룹은 일반 선형 GL K {\ 에 항목이 있는 n × {\ n n개의 가역 행렬의이름 }(n입니다
커널, 이미지 및 랭크-널리티 정리
f : → W V는 선형이므로 커널과 의 이미지 또는 범위를 다음과 같이 정의합니다.
은(는 V {\ V의 하위 공간이고 은(는) 의 하위 공간입니다 다음 차원 공식을 랭크-널리티 정리라고 합니다.
숫자 ( 을(를) 의 라고도 하며 로 쓰거나 때로는 ρ 로 쓰거나 숫자 을(를) f의 무효라고 하며 으로 쓰임 ( \ { (f) (f \nu입니다 V} W가 유한 차원인 경우 가 선택되었고 f f}이행렬 A A}로표시되면 f f}의 및 무효는 행렬 의 랭크 및 무효와 같습니다. 각각.
코커널
선형 변환 의 하위 불변량 : → W f:은(는) 다음과 같이 정의되는 코커널입니다.
커널에 대한 이중 개념입니다. 커널이 도메인의 하위 공간이듯이, 공동 커널은 타겟의 몫 공간이 됩니다.형식적으로는 정확한 순서를 가지고 있습니다.
이들은 다음과 같이 해석될 수 있습니다: 해를 구하는 선형 방정식 f(v) = w가 주어지면,
- 커널은 동차방정식인 f(v) = 0에 대한 해의 공간이고, 그 차원은 해의 공간에서 자유도의 수이다, 만약 그것이 비어있지 않다면;
- 공동 kernel은 솔루션이 만족해야 하는 제약 조건의 공간이며, 그 차원은 독립 제약 조건의 최대 개수입니다.
코커널의 차원과 이미지의 차원(순위)은 대상 공간의 차원과 합산됩니다.유한 차원의 경우 몫 공간 W/f(V)의 차원이 대상 공간의 차원에서 이미지의 차원을 뺀 것임을 의미합니다.
간단한 예로, f(x, y) = (0, y)로 주어진 지도 f: R → R을 생각해 보십시오.그 다음 식 f(x, y) = (a, b)가 해를 가지려면 = 0(1개의 제약 조건)을 가져야 하며, 그 경우 해 공간은 (x, b) 또는 이와 동등하게 표시되는 (0, b) + (x, 0), (1개의 자유도)가 됩니다.커널은 부분공간 (x, 0) < V: x의 값은 해에서의 자유도이고, 반면에 코커널은 지도 W → R, ↦( 로 표현될 수 있습니다 벡터 (a, b)가 주어지면 a의 값은 해가 존재하는 것에 방해가 됩니다.
무한 차원의 경우를 나타내는 예는 지도 f에 의해 제공됩니다: R → R { ↦ { b {\ \leftn}\ \leftn}\ b = a > 0.이미지는 첫 번째 요소가 0인 모든 시퀀스로 구성되며 따라서 코커널은 첫 번째 요소가 동일한 시퀀스 클래스로 구성됩니다.따라서 커널의 차원이 0인 반면(0 수열만 0 수열에 매핑함), 공동 커널의 차원은 1입니다.도메인과 대상 공간이 같기 때문에, 순위와 커널의 차원을 합하면 순위와 공동 kernel의 차원(ℵ 0+ = ℵ + =\그러나 무한 차원의 경우에는 커널과 내형의 공동 kernel이 동일한 차원(0 ≠ 1)을 갖는다고 추론할 수 없습니다.역상황은 지도 h에 대해 R → R,{ ↦ c to c = a.이미지는 전체 대상 공간이므로 공동 커널은 차원 0을 갖지만 첫 번째 요소만 0이 아닌 모든 시퀀스를 0 시퀀스에 매핑하므로 커널은 차원 1을 갖습니다.
색인
유한 차원 커널과 코커널을 갖는 선형 연산자의 경우 인덱스를 다음과 같이 정의할 수 있습니다.
유한 차원 벡터 공간 간의 변환의 경우, 이는 단지 순위-nullity에 의한 차이 dim(V) - dim(W)입니다.이것은 솔루션의 수 또는 제약 조건의 수를 나타냅니다. 더 큰 공간에서 더 작은 공간으로 매핑하는 경우 맵이 위에 있을 수 있으므로 제약 조건이 없어도 자유도를 가질 수 있습니다.반대로, 더 작은 공간에서 더 큰 공간으로 매핑하는 경우, 지도 위에 있을 수 없으므로 자유도가 없어도 제약이 발생합니다.
연산자 지수는 정확히 2항 복소수 0 → V → W → 0의 오일러 특성입니다. 연산자 이론에서 프레드홀름 연산자 지수는 연구의 대상이며 주요 결과는 아티야-싱어 지수 정리입니다.
선형 변환의 대수적 분류
선형 맵의 어떤 분류도 포괄적일 수 없습니다.다음의 불완전한 목록은 벡터 공간에 대한 추가적인 구조가 필요하지 않은 몇 가지 중요한 분류를 열거합니다.
필드 F 위의 벡터 공간을 V와 W라고 하고 T: V → W를 선형 맵이라고 합니다.
단형론
다음과 같은 동등한 조건 중 하나라도 참일 경우 이는 주입형 또는 단형이라고 합니다.
- T는 집합 지도로서 일대일입니다.
- kerT = {0}
- dim(ker T) = 0
- 즉, 임의의 벡터 공간 U와 임의의 쌍의 선형 맵 R: U → V 및 S: U → V에 대해 방정식 TR = TS는 R = S를 의미합니다.
- T는 좌가역이며, 즉 선형 맵 S: W → V가 존재하므로 ST는 V의 항등식 맵이 됩니다.
에피모피즘
이는 다음과 같은 동등한 조건 중 하나라도 참일 경우 주관적 또는 에피모피즘이라고 합니다.
- 집합 지도로 표시됩니다.
- 코커 T = {0}
- 이것은 서사적이거나 오른쪽 cancell이 가능합니다. 즉, 임의의 벡터 공간 U와 임의의 쌍의 선형 맵 R: W → U 및 S: W → U에 대해, 방정식 RT = ST는 R = S를 의미합니다.
- T는 우반전 가능하며, 즉 선형 맵 S: W → V가 존재하므로 TS는 W의 항등식 맵이 됩니다.
동형 사상
이는 좌, 우 둘 다 가역적이면 동형이라고 합니다.이것은 T가 일대일이면서 동시에 (집합들의 사영) 또는 T가 서사적이고 단성적이어서 쌍모음이 되는 것과 동일합니다.
T: V → V가 내형이면 다음과 같습니다.
- 일부 양의 정수 n에 대해 T의n n반복 횟수가 동일하게 0이면 T는 0의 힘을 갖는다고 합니다.
- 만약 T = T이면, T는 idempotentive라고 합니다.
- 만약 T = kI이고, 여기서 k는 어느 정도의 스칼라라면, T는 스케일링 변환 또는 스칼라 곱셈 맵이라고 합니다. 스칼라 행렬을 참조하십시오.
기초변경
행렬이 A인 내형인 선형 맵이 주어지면, 공간의 기저 B에서 벡터 좌표 [u]를 [v] = A[u]로 변환합니다.벡터가 B(vectors는 반변형)의 역으로 변하면 역변환은 [v] = B[v']가 됩니다.
이것을 첫번째 표현식에 대입하면
따라서 새로운 기저의 행렬은 A' = BAB이며, 주어진 기저의 행렬은 B입니다.
따라서 선형 맵은 1-공-1-대변형 객체 또는 유형 (1, 1) 텐서라고 합니다.
연속성
위상 벡터 공간 간의 선형 변환(예: 노름 공간)은 연속적일 수 있습니다.도메인과 코드 도메인이 같으면 연속 선형 연산자가 됩니다.노름 선형 공간의 선형 연산자는 도메인이 유한 차원일 때와 같이 유계일 경우에만 연속입니다.[18]무한 차원 도메인에는 불연속 선형 연산자가 있을 수 있습니다.
무한하고, 따라서 불연속적인 선형 변환의 예로는 수프리움 노름(값이 작은 함수는 값이 큰 도함수를 가질 수 있는 반면 0의 도함수는 0)을 갖춘 매끄러운 함수의 공간에 대한 미분이 있습니다.구체적인 예를 들어 sin(nx)/n은 0으로 수렴하지만, 그 도함수 cos(nx)는 0으로 수렴하지 않으므로 미분은 0에서 연속적이지 않습니다(그리고 이 인수의 변형에 의해 어느 곳에서도 연속적이지 않습니다).
적용들
선형 맵의 특정한 응용은 컴퓨터 그래픽에서 수행되는 것과 같은 기하학적 변환을 위한 것으로, 변환 행렬을 사용하여 2D 또는 3D 객체의 변환, 회전 및 스케일링을 수행합니다.선형 매핑은 또한 변화를 설명하는 메커니즘으로 사용됩니다. 예를 들어 미적분학에서는 도함수에 해당합니다. 또는 상대성 이론에서는 참조 프레임의 국소 변환을 추적하는 장치로 사용됩니다.
이러한 변환의 또 다른 적용은 중첩 루프 코드의 컴파일러 최적화와 컴파일러 기술의 병렬화에 있습니다.
참고 항목
- 추가 지도 – Z-모듈 동형
- Antiline Map – 켤레 균질 가법 지도
- Bend function – 특수 유형의 부울 함수
- 유계 연산자 – 위상 벡터 공간 간의 선형 변환
- 코시 함수식 – 함수식
- 연속 선형 연산자
- 선형 기능 – 벡터 공간에서 스칼라 필드까지의 선형 맵방향 에 대한 하는 페이지
- 선형 등각법 – 거리 보존 수학적 변환방향 에 대한 하는 페이지
메모들
- ^ "V에서 V로의 선형 변환은 종종 V의 선형 연산자라고 불립니다." Rudin 1976, 페이지 207
- ^ V와 W를 두 개의 실수 벡터 공간이라 하자.a를 V에서 W로 매핑하는 것을 '선형 매핑' 또는 '선형 변환' 또는 '선형 연산자'[...]라고 합니다.
(+ ) + ) = + }
a(λ ) 모 V 및 모든실제 에 mathbf λ - ^ 루딘 1991년 p.
다음은 증명이 너무 쉬워 생략할 수 있는 선형 매핑 λ →Y {\ \to 의 몇 가지 속성입니다. ⊂X {\ X와 ⊂Y {\B\ Y를 가정합니다 - ^ 루딘 1991년 14쪽.이제 X와 Y가 동일한 스칼라 필드 위의 벡터 공간이라고 가정합니다.매핑 λ: → 는 λ x + y = λ + λ y =\textbf {= X 및 모든 스칼라 \beta }. \}이가) 선형인 경우에는 (x {\이가) 라 x {\textstyle \Lambda 로 쓰는 경우가 많습니다.
- ^ 루딘 1976, 페이지 206.벡터 공간 X의 벡터 공간 Y로의 매핑 A는 다음과 같은 경우에 선형 변환이라고 합니다: ( 1+ 2 )= x + A A( )= } _) =모든 X { _{2mathbf 및 모든 스칼라 c에 대해 _{2}\in A가 선형인 경우 ( A 대신 x 로 쓰는 경우가 많습니다.
- ^ 루딘 1991년 14쪽.X의 스칼라 필드에 대한 선형 매핑을 선형 함수라고 합니다.
- ^ "terminology - What does 'linear' mean in Linear Algebra?". Mathematics Stack Exchange. Retrieved 2021-02-17.
- ^ 윌란스키 2013, 21-26쪽.
- ^ a b Kubrussly 2001, 페이지 57.
- ^ a b Schechter 1996, pp. 277-280
- ^ 루딘 1976, p. 210 {x …,x 를 각각 벡터 공간 X와 Y의 기저라고 가정하자.그런 다음 A∈ ({\ A L은 다음과 같이 {\의 집합을 결정합니다.mbynmatrix라고 하는 m 행과 n 열로 이루어진 직사각형 배열로 이러한 숫자를 나타내는 것이 편리합니다.벡터 x {y 1 …, y A}}{\ {y_mathbf }\})의 j {_{j}가[ 의th j 열에 나타남을 합니다. 벡터A x j {\mathbf {j}}를 때때로 다음과 같이 부릅니다 의 열 벡터 이 용어를 사용하면 A의 범위가[ 의 열 벡터에 의해 확장됩니다
- ^ Axler (2015) 페이지 52, § 3.3
- ^ Tu (2011), p. 19, § 3.1
- ^ Horn & Johnson 2013, 0.2.3 행렬 또는 선형 변환과 관련된 벡터 공간, 페이지 6
- ^ a b Katznelson & Katznelson (2008) p. 52, § 2.5.1
- ^ a b Halmos (1974) p. 90, § 50
- ^ Nistor, Victor (2001) [1994], "Index theory", Encyclopedia of Mathematics, EMS PressNistor, Victor (2001) [1994], "Index theory", Encyclopedia of Mathematics, EMS Press"지수 이론의 주된 질문은 프레드홀름 연산자 클래스에 지수 공식을 제공하는 것입니다...색인 이론은 M. F. 이후에야 독자적인 주제가 되었습니다.아티야와 나.가수가 색인 정리를 발표했습니다."
- ^ 루딘 1991, p. 15 1.18 정리λ }을위상 벡터 공간 X에 대한 선형 함수라고 하자. X에 대해 ≠ 0 이라고 가정합니다 그러면 다음 네 가지 속성은 각각 다른 세 속성을 의미합니다.
- {\ \Lambda이가) 연속입니다.
- Null 공백 λ 이(가) 닫혔습니다.
- ( 이(가) X에서 조밀하지 않습니다.
- \Lambda은(는) 0의 일부 인접 V에서 경계를 이루고 있습니다.
서지학
- Axler, Sheldon Jay (2015). Linear Algebra Done Right (3rd ed.). Springer. ISBN 978-3-319-11079-0.
- Bronshtein, I. N.; Semendyayev, K. A. (2004). Handbook of Mathematics (4th ed.). New York: Springer-Verlag. ISBN 3-540-43491-7.
- Halmos, Paul Richard (1974) [1958]. Finite-Dimensional Vector Spaces (2nd ed.). Springer. ISBN 0-387-90093-4.
- Horn, Roger A.; Johnson, Charles R. (2013). Matrix Analysis (Second ed.). Cambridge University Press. ISBN 978-0-521-83940-2.
- Katznelson, Yitzhak; Katznelson, Yonatan R. (2008). A (Terse) Introduction to Linear Algebra. American Mathematical Society. ISBN 978-0-8218-4419-9.
- Kubrusly, Carlos (2001). Elements of operator theory. Boston: Birkhäuser. ISBN 978-1-4757-3328-0. OCLC 754555941.
- Lang, Serge (1987), Linear Algebra (Third ed.), New York: Springer-Verlag, ISBN 0-387-96412-6
- Rudin, Walter (1973). Functional Analysis. International Series in Pure and Applied Mathematics. Vol. 25 (First ed.). New York, NY: McGraw-Hill Science/Engineering/Math. ISBN 9780070542259.
- Rudin, Walter (1976). Principles of Mathematical Analysis. Walter Rudin Student Series in Advanced Mathematics (3rd ed.). New York: McGraw–Hill. ISBN 978-0-07-054235-8.
- Rudin, Walter (1991). Functional Analysis. International Series in Pure and Applied Mathematics. Vol. 8 (Second ed.). New York, NY: McGraw-Hill Science/Engineering/Math. ISBN 978-0-07-054236-5. OCLC 21163277.
- Schaefer, Helmut H.; Wolff, Manfred P. (1999). Topological Vector Spaces. GTM. Vol. 8 (Second ed.). New York, NY: Springer New York Imprint Springer. ISBN 978-1-4612-7155-0. OCLC 840278135.
- Schechter, Eric (1996). Handbook of Analysis and Its Foundations. San Diego, CA: Academic Press. ISBN 978-0-12-622760-4. OCLC 175294365.
- Swartz, Charles (1992). An introduction to Functional Analysis. New York: M. Dekker. ISBN 978-0-8247-8643-4. OCLC 24909067.
- Tu, Loring W. (2011). An Introduction to Manifolds (2nd ed.). Springer. ISBN 978-0-8218-4419-9.
- Wilansky, Albert (2013). Modern Methods in Topological Vector Spaces. Mineola, New York: Dover Publications, Inc. ISBN 978-0-486-49353-4. OCLC 849801114.
 (는)
(는) 













 (는) 선형 맵입니다.
(는) 선형 맵입니다.




 X
X 
 (가) 유한
(가) 유한 
 (는) 선형 맵입니다.
(는) 선형 맵입니다.













![{\textstyle \left[\mathbf {v} \right]_{B'}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38ce4e66d088a57d8adb2aadc461213818bc3220)
![{\textstyle A'\left[\mathbf {v} \right]_{B'}=\left[T\left(\mathbf {v} \right)\right]_{B'}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d40bbccc105af68b575ef57b62b1e1943c478aaa)
![{\textstyle P^{-1}AP\left[\mathbf {v} \right]_{B'}=\left[T\left(\mathbf {v} \right)\right]_{B'}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c713b4830cf922213fe7907677ae35be5fffcfc)























![{\displaystyle B\left[v'\right]=AB\left[u'\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2855717373418c2c2134151c0d0f4d5957292f8)
![{\displaystyle \left[v'\right]=B^{-1}AB\left[u'\right]=A'\left[u'\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65eb8aa4babed0054fcf025303d23fd58309bf7e)







![{\displaystyle [A]={\begin{bmatrix}a_{1,1}&a_{1,2}&\ldots &a_{1,n}\\a_{2,1}&a_{2,2}&\ldots &a_{2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{m,1}&a_{m,2}&\ldots &a_{m,n}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f53d08efeacd19a7270d82ee81484d772f4e8ef)



![{\textstyle [A]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efc7c42d7e9f789e2b3384a4f718faddeb0f2119)



