실제 좌표 공간

이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "실제 좌표 공간" – 뉴스 · 신문 · 책 · 학자 · JSTOR (2013년 4월) (이 템플릿 메시지를 제거하는 방법과 시기 학습)

수학에서 치수 n의 실제 좌표 공간인ⁿ R(//ːrˈn/ar-EN) 또는 ${\displaystyle {}^{}}$ n ${\$은 실제 숫자에 대한 좌표 공간이다. 이것은 실수의 n-tules 집합(실수의 순서)이라는 것을 의미한다. 성분별 덧셈과 스칼라 곱셈으로 실제 벡터 공간이다.

전형적으로 유클리드 공간의 요소들에 대한 데카르트 좌표는 실제 좌표 공간을 형성한다. 이것은 좌표 공간의 명칭과 좌표공간으로 작업할 때 기하학적 용어들이 자주 사용된다는 사실을 설명한다. 예를 들어 R은² 비행기다.

좌표 공간은 그 요소들이 유클리드 공간에서 지점을 찾고 그것들과 함께 계산하는 것을 허용하기 때문에 기하학과 물리학에서 널리 사용된다.

정의 및 구조

자연수 n에 대해, 집합 R은ⁿ 실수(R)의 모든 n-tule로 구성된다. 그것은 "n차원 실제 공간" 또는 "진짜 n-공간"이라고 불린다.

따라서ⁿ R의 요소는 n-투플이며, 기록되어 있다.

${\displaystyle(x_{1},x_{2},\ldots,x_{n})}$

여기서 각 x는_i 실제 숫자다. 따라서, 다변량 미적분학에서, 몇 개의 실제 변수의 함수 영역과 실제 벡터 값 함수의 코도메인은 일부 n에 대한ⁿ R의 하위 집합이다.

실제 n-space에는 다음과 같은 몇 가지 추가 특성이 있다.

• 구성 요소별 덧셈과 스칼라 곱셈으로 실제 벡터 공간이다. 모든 n차원 실제 벡터 공간은 그것에 이형화 되어 있다.
• 도트 제품(부품의 용어 제품별 용어 합계)으로 내부 제품 공간이다. 모든 n차원 실제 내부 제품 공간은 그것에 이형화된다.
• 모든 내부 제품 공간으로서 위상학적 공간이며, 위상학적 벡터 공간이다.
• 그것은 유클리드 공간이고 진짜 아핀 공간이며, 모든 유클리드 공간이나 아핀 공간은 그것에 이형화된다.
• 다지관은 분석 다지관이며, 정의상 다지관은 R의ⁿ 개방된 부분 집합에 대해 이형성이기 때문에 모든 다지관의 프로토타입으로 간주할 수 있다.
• 대수적 품종이며, 모든 실제 대수적 품종은 R의ⁿ 부분집합이다.

이러한ⁿ R의 특성과 구조는 통계학, 확률론, 그리고 물리학의 많은 부분과 같은 수학의 거의 모든 영역과 응용영역에서 그것을 기본으로 만든다.

여러 변수의 함수의 영역

n개의 실제 변수의 함수 f(x₁, x₂, …, x_n)는 Rⁿ(R을ⁿ 도메인으로 하는)의 함수로 간주할 수 있다. 실제 n-공간을 사용하면 별도로 고려하는 여러 변수 대신 표기법을 단순화하고 합리적인 정의를 제시할 수 있다. n = 2의 경우 다음 형식의 함수 구성을 고려하십시오.

${\displaystyle F(t)=f(g_{1}(t), g_{2}(t),}$

여기서 함수 g와₁ g는₂ 연속적이다. 만약

∀x₁ ∈ R : f(x₁, ·) 연속 (x₂ by x)

∀x₂ ∈ R : f(·, x) 연속₂ (x₁ by)

그렇다면 F가 반드시 연속적인 것은 아니다. 연속성은 보다 강한 조건이다: 자연 R² 위상에서 f의 연속성(아래에서 설명됨), 또한 다변량 연속성이라고도 하며, 이는 구성 F의 연속성에 충분하다.

이 구간은 확장이 필요하다. 추가하면 도움이 된다. (2013년 4월)

벡터 공간

좌표 공간 R은ⁿ 선형성의 구조를 추가하여 실수의 영역 위에 n차원 벡터 공간을 형성하며, 여전히 R로ⁿ 표기되는 경우가 많다. 벡터 공간으로서의 R에서의ⁿ 연산은 일반적으로 다음과 같이 정의된다.

${\displaystyle \mathbf {x} +\mathbf {y} =(x_{1}+y_{1},x_{2}+y_{2},\ldots ,x_{n}+y_{n}}}}}}}}}$

${\displaystyle \mathbf {x} =(\mathbf {x},\math x_{1},\message x_{2},\ldots ,\message x_{n}).}$

영점 벡터는 다음에 의해 주어진다.

${\displaystyle \mathbf {0} = (0,0,\ldots ,0)}$

벡터 x의 가법 역은 다음과 같다.

${\displaystyle -\mathbf {x} =(-x_{1},-x_{2},\ldots ,-x_{n}).}$

이 구조는 어떤 n차원 실제 벡터 공간도 벡터 공간 R에ⁿ 대해 이형성적이기 때문에 중요하다.

행렬 표기법

표준 행렬 표기법에서 R의ⁿ 각 요소는 일반적으로 열 벡터로 표기된다.

${\displaystyle \mathbf {x} ={\\bmatrix}x_{1}\\x_{2}\\\\vdots \x_{n}\end{bmatrix}}}}}}$

그리고 때로는 행 벡터로서 다음과 같이 한다.

${\displaystyle \mathbf {x} ={\put{bmatrix}x_{1}x_{2}&\cdots &x_{n}\end{bmatrix}}}.}$

좌표 공간 R은ⁿ 모든 n × 1 열 벡터 또는 모든 1 × n 행 벡터의 공간으로 해석될 수 있으며, 추가 및 스칼라 곱의 일반적인 매트릭스 연산이 있다.

그런ⁿ 다음 R에서^m R로 선형 변환은 m × n 행렬로 기록될 수 있으며, 이 행렬은 왼쪽 곱셈을 통해 R의ⁿ 요소와 오른쪽 곱셈을 통해 R의^m 요소(행ⁿ 벡터일 때)에 작용한다. 행렬 곱셈의 특별한 경우인 왼쪽 곱셈의 공식은 다음과 같다.

${\displaystyle (A{\mathbf {x}}}_{k}=\sum \limits _{l=1}^{n}A_{kl}x_{l}}}}}}}}$

선형 변환은 연속 함수(아래 참조)이다. 또한 행렬의 순위가 m과 같을 경우에만 행렬은ⁿ R에서^m R까지 열린 지도를 정의한다.

표준기준

좌표 공간 R에는ⁿ 다음과 같은 표준 기준이 있다.

${\displaystyle {\begin{aligned}\mathbf {e} _{1}&=(1,0,\ldots ,0)\\\mathbf {e} _{2}&=(0,1,\ldots ,0)\\&{}\;\;\vdots \\\mathbf {e} _{n}&=(0,0,\ldots ,1)\end{aligned}}}$

이것이 기본임을 확인하려면 R의ⁿ 임의 벡터는 양식에 고유하게 기록될 수 있다는 점에 유의하십시오.

${\displaystyle \mathbf {x} =\sum _{i=1}^{n}x_{i}\mathbf {e} _{i}.}$

기하학적 특성 및 용도

오리엔테이션

실수는 다른 많은 분야와 달리 순서가 정해진 분야를 구성한다는 사실은 R에ⁿ 방향 구조를 산출한다. R의ⁿ 모든 전체 순위 선형 지도는 그 자체로 그 행렬의 결정 인자의 부호에 따라 공간의 방향을 유지하거나 반전시킨다. 하나의 좌표(또는 다시 말하면 기초의 요소)를 허용하면 결과 방향은 순열의 패리티에 따라 달라진다.

그 안에 있는 R이나ⁿ 영역의 차이점들은, 자코비안 0을 피하기 위한 그들의 덕성에 의해서, 방향 보존과 방향 전환에도 분류된다. 그것은 전기 역학을 포함하는 미분형 이론에 중요한 결과를 가져온다.

이 구조의 또 다른 표현은 R의ⁿ 점반사가 n의 균등도에 따라 다른 성질을 갖는다는 것이다. 짝수 n의 경우 방향을 유지하는 반면 홀수 n의 경우 방향을 반대로 한다(부적절한 회전 참조).

아핀 공간

아핀 스페이스로 이해되는 R은ⁿ 벡터 스페이스로서의 R이ⁿ 번역에 의해 작용하는 동일한 공간이다. 반대로 벡터는 "두 점 사이의 차이"로 이해되어야 하며, 일반적으로 두 점을 연결하는 방향 선 세그먼트에 의해 설명된다. 그 구별은 어디서든 번역이 가능하기 때문에, 어편 n-space에서 기원이 어디로 가야 하는지에 대한 표준적인 선택이 없다고 말한다.

볼록도

R과ⁿ 같은 실제 벡터 공간에서는 그 벡터의 모든 비 음의 선형 결합을 포함하는 볼록콘을 정의할 수 있다. 아핀 공간에서의 해당 개념은 볼록한 조합(합계 1인 비 음의 선형 조합)만 허용하는 볼록 집합이다.

유니버설 대수학 언어에서 벡터 공간은 유한 벡터 합계에 해당하는 유한계수의 범용 벡터 공간 R에^∞ 대한 대수인 반면, 아핀 공간은 이 공간에서의 범용 아핀 하이퍼플레인 위에 대한 대수(총합 1에 이르는 유한 시퀀스의 경우), 원뿔은 범용 직교체에 대한 대수인 것이다. (비 음수의 유한 시퀀스) 및 볼록스 집합은 범용 심플렉스(비 음수의 유한 시퀀스 1)에 대한 대수다. 이 기하학적 구조는 "좌표에 대한 제약이 있는 (가능) 합"의 관점에서 공리를 강조한다.

볼록 분석의 또 다른 개념은 R에서ⁿ 실제 숫자에 이르는 볼록함수인데, 이는 동일한 계수를 가진 점의 볼록한 조합에 대한 값과 값의 합 사이의 불평등을 통해 정의된다.

유클리드 공간

도트 제품

${\displaystyle \mathbf {x} \cdot \mathbf {y} =\sum _{n_{n_{n}y_{n}={n_{i}=x_{1}y_{1}+x_{2}+}y_{2}+}+}+{n}y_{n}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

벡터 공간 R에서ⁿ 표준 x = √x ⋅ x를 정의한다. 모든 벡터에 유클리드 규범이 있는 경우, 어떤 점의 쌍에 대해 거리

${\displaystyle d(\mathbf {x},\mathbf {y})=\mathbf {x} -\mathbf {y}\ ={\sqrt {\\sum _{i=1}^{n}(x_{i}-y_{i}^}^{2}}:$

정의되며, 부속물 구조 외에 R에ⁿ 미터법 공간 구조를 제공한다.

벡터 공간구조의 경우 도트 제품과 유클리드 거리는 특별한 설명 없이 R에ⁿ 존재하는 것으로 가정한다. 그러나, 엄밀히 말하면, 진짜 n-공간과 유클리드 n-공간은 구별되는 사물이다. 임의의 유클리드 n-공간은 도트 제품과 유클리드 거리가 위에 나타낸 형태를 갖는 좌표계를 가지고 있는데, 이를 카르테시안이라고 한다. 그러나 유클리드 공간에는 많은 카르테시안 좌표계가 있다.

반대로 유클리드 메트릭스에 대한 위의 공식은 R에ⁿ 표준 유클리드 구조를 정의하지만, 그것만이 가능한 것은 아니다. 실제로 어떤 양립형 q는 그 자체의 「거리」 √q(x - y)를 정의하고 있지만, 그 의미에서는 유클리드형과 크게 다르지 않다.

${\displaystyle \exists C_{1}}0,\exist C_{2}}0,\all \mathbf {x},\mathbf {y} \in \mathb {R}^{n}:C_{1}d(\mathbf {x},\mathbf {y} )\leq {q(\mathbf {x} -\mathbf {y})}}}\leq C_{2}d(\mathbf {x},\mathbf {y}).}$

이러한 메트릭의 변경은 메트릭의 속성 중 일부를 보존한다. 예를 들어, 완전한 메트릭 공간이라는 속성이 그것이다. 이는 또한 R의ⁿ 어떤 전체 순위 선형 변환 또는 그 부속 변환은 일부 고정 C보다₂ 거리를 더 확대하지 않으며, 고정된 유한 수 곱하기인 1㎛ C배보다₁ 거리를 작게 만들지 않는다는 것을 의미한다.^{[clarification needed]}

전술한 미터법 함수의 등가성은 √q(x - y)를 M(x - y)으로 대체한 경우 유효하며, 여기서 M은 도 1의 볼록 양성 동질 함수, 즉 벡터 노멀(vector norm)이다(유용한 예는 Minkowski 거리 참조). R에ⁿ 대한 어떤 "자연적" 측정기준도 유클리드 측정기준과 특별히 다르지 않다는 이 사실 때문에, R은ⁿ 전문적인 수학작품에서도 유클리드 n-공간과 항상 구별되는 것은 아니다.

대수기하학 및 미분기하학에서

다지관의 정의는 그 모델 공간이 R이어야ⁿ 한다는 것을 요구하지 않지만, 이 선택은 미분 기하학에서 가장 흔하고 거의 배타적인 것이다.

반면에 휘트니 내장 이론은 R에^2m 실제로 다른 m-차원 다지관을 내장할 수 있다고 기술하고 있다.

이 구간은 확장이 필요하다. 추가하면 도움이 된다. (2013년 4월)

기타 출연

R에서ⁿ 고려된 다른 구조로는 사이비-유클리드 공간, 공감 구조(짝수 n), 접촉 구조(이상 n) 중 하나가 있다. 이 모든 구조물은 좌표가 없는 방식으로 정의할 수 있지만 좌표에 표준(그리고 합리적으로 간단한) 형태를 허용한다.

R은ⁿ 또한 복잡한 결합에 불변하는 C의ⁿ 실제 벡터 하위 공간이다. 또한 복합화를 참조하라.

폴리토페스(Rⁿ)

임의의 n에 대해 R 공간에서ⁿ 간단한 표현을 하고 실제 n-공간에서 어떤 부속 좌표계를 시각화하는 데 사용할 수 있는 3개의 폴리토페 가족이 있다. 하이퍼큐브의 꼭지점에는 좌표(x₁, x₂, …, x_n)가 있으며, 각 x는_k 일반적으로 0 또는 1의 두 값 중 하나만 차지한다. 그러나 0과 1 대신 임의의 두 숫자를 선택할 수 있다(예: -1과 1). n-하이퍼큐브는 실제 라인에서 동일한 간격(단위 간격 [0,1] 등)의 데카르트 산물로 생각할 수 있다. n차원 부분 집합으로서 2n 불평등 시스템을 사용하여 설명할 수 있다.

${\displaystyle {\displaystyle \begin{array}{c}0\end{array}}}$≤ ${\displaystyle {\displaystyle \begin{array}{c}{}_{}\end{array}}}$ ${\displaystyle {\displaystyle \begin{array}{c}{1\mathrm{}}_{}\end{array}}}$≤ ${\displaystyle {\displaystyle \begin{array}{c}1\end{array}}}$ ${\displaystyle {\displaystyle \begin{array}{}⋮\\ \end{array}}}$ ${\displaystyle {\displaystyle \begin{array}{}0\\ \mathrm{}\end{array}}}$ ${\displaystyle {\displaystyle \begin{array}{c}\le \end{array}}}$ ${\displaystyle {\displaystyle \begin{array}{c}{}_{}\end{array}}}$ ${\displaystyle {\displaystyle \begin{array}{c}{}_{}\end{array}}}$ ${\displaystyle {\displaystyle \begin{array}{c}1\end{array}}}$ ${\$ \\displaystyle ${\displaysty}\\\leq x_{1}\n}\leq 1\end$}}}([0,1]의 경우)

${\displaystyle {\displaystyle \begin{array}{c}{x}_{}\end{array}}}$ ${\displaystyle {\displaystyle \begin{array}{c}{1\mathrm{}}_{}{}_{}\end{array}}}$≤ ${\displaystyle {\displaystyle \begin{array}{c}1\\ \\ {}_{}\\ \\ \\ \le {}_{}\end{array}}}$ ${\displaystyle {\displaystyle \begin{array}{c}\mathrm{x}\end{array}}}$ ${$ 1 {\$displaystyle \displaystyle {\displaystyle {\n1} \leq$ 1$\\\\\vdots$\\\\\\\$n} \leq 1\end{n$}}}}([-1]의 경우)

크로스 폴리토프의 각 정점에는 일부 k의 경우 x 좌표가_k ±1이고 다른 모든 좌표는 0(예: k번째 표준 기준 벡터 위로 표시)이 있다. 이것은 하이퍼큐브의 이중 폴리토프 입니다. n차원 부분 집합으로서 절대값 연산을 사용하는 단일 불평등으로 설명할 수 있다.

$\displaystyle \sum \sum _{k=1}^{n} x_{k} \leq 1\\}$

그러나 이것은 또한 2개의ⁿ 선형 불평등 시스템으로 표현될 수 있다.

단순히 열거할 수 있는 좌표를 가진 세 번째 폴리토프는 표준 심플렉스인데, 그 정점들은 표준 기준 벡터와 원점 (0, 0, …, 0)이다. n차원 부분 집합으로서, 그것은 n + 1 선형 불평등의 시스템으로 설명된다.

${\displaystyle {\req ×_{1}\\\vdots\\\\\0\\\\\0\\leq x_{n}\\sum \sum \{k=1}^{n}x_{k}\leq 1\end}}}}}}}}}}}}}$

모든 "기호"를 "<"로 교체하면 이러한 폴리토프의 내부가 된다.

위상학적 특성

R의ⁿ 위상 구조(표준 위상, 유클리드 위상 또는 통상 위상이라 한다)는 데카르트 제품에서만 얻을 수 있는 것이 아니다. 그것은 또한 위에서 논의한 유클리드 메트릭스에 의해 유도된 자연 위상과 동일하다. 세트에는 각각의 포인트 주위에 열린 공이 포함되어 있는 경우에만 유클리드 위상에서 개방된다. 또한 R은ⁿ 선형 위상학 공간(위 선형 지도의 연속성 참조)이며, 그 선형 구조와 호환되는 (비경쟁적) 위상은 단 하나뿐이다. 등각도가 아닌 R에서ⁿ 그 자체로 열린 선형 지도가 많으므로, R에는 동일한ⁿ 위상에 해당하는 유클리드 구조물이 많이 있을 수 있다. 사실, 그것은 선형 구조에도 크게 의존하지 않는다: 그 자체에는 많은ⁿ R의 비선형 차이점들이 있다. 또는 유클리드 오픈 볼이나 하이퍼큐브 내부와 같은 그것의 부분들.

R은ⁿ 위상학적 차원 n을 가지고 있다. 표면적과는 거리가 먼 R의ⁿ 위상에 관한 중요한 결과는 브루워의 영역침입이다. R의ⁿ 다른 열린 부분 집합에 대해 동형인 R의ⁿ 하위 집합(하위 공간 위상)은 그 자체로 개방된다. 이에 대한 즉각적인 결과는, 그럼에도 불구하고 증명하기 어려운 직관적인 "불확실한" 결과인 m ≠ n이면 R이^m R에ⁿ 대해 동형체가 아니라는 것이다.

위상학적 차원의 차이에도 불구하고, 그리고 순진한 인식과는 반대로, R에ⁿ 지속적으로 그리고 굴욕적으로 더 작은 차원의^{[clarification needed]} 실제 공간을 매핑하는 것이 가능하다. 연속적인 공간 채우기 곡선(R의¹ 이미지)이 가능하다.^{[clarification needed]}

예

빈 열 벡터, R의0 유일한 요소

R1

n ≤ 1

0 ≤ n ≤ 1의 경우는 새로운 것을 제공하지 않는다: R은¹ 실제 선인 반면, R⁰(빈 기둥 벡터를 포함하는 공간)은 0 벡터 공간으로 이해되는 싱글톤이다. 그러나 이러한 것들을 서로 다른 n을 기술하는 이론의 사소한 사례로 포함시키는 것이 유용하다.

n = 2

이 구간은 확장이 필요하다. 추가하면 도움이 된다. (2013년 4월)

n = 3

이 구간은 확장이 필요하다. 추가하면 도움이 된다. (2013년 4월)

n = 4

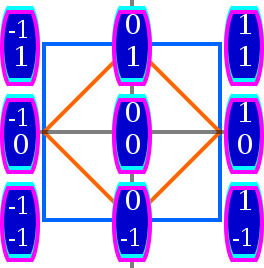
R은⁴ 각 x가_k 0 또는 1인 16점(x₁, x₂, x₃, x₄)이 4-하이퍼큐브인 큐브(위 참조)의 정점이라는 사실을 이용하여 상상할 수 있다.

R의⁴ 첫 번째 주요 용도는 스페이스타임 모델이다: 3개의 공간 좌표와 1개의 시간 좌표. 이것은 보통 상대성 이론과 관련이 있지만, 갈릴레이 이후 그러한 모델에 4차원이 사용되었다. 그러나 이론의 선택은 다른 구조로 이어진다: 갈릴레이 상대성에서는 t 좌표가 특권이지만 아인슈타인 상대성에서는 그렇지 않다. 특수상대성이란 민코프스키 공간을 배경으로 한다. 일반 상대성 이론은 곡선 공간을 사용하며, 대부분의 실용적인 목적을 위해 곡선 지표를 가진 R로⁴ 생각할 수 있다. 이러한 구조 중 어느 것도 R에⁴ 대한 (긍정적-확정적) 측정기준을 제공하지 않는다.

유클리드 R은⁴ 수학자들의 관심을 끌기도 하는데, 예를 들어 4차원 실제 대수학 그 자체인 쿼터니온과의 관계 때문이다. 자세한 내용은 4차원 유클리드 공간의 회전을 참조하십시오.

미분 기하학에서, n = 4는 R이ⁿ 비표준 미분 구조를 인정하는 유일한 경우: 이국적인 R을⁴ 참조한다.

Rⁿ 상의 규범

벡터 공간 R에서ⁿ 많은 규범을 정의할 수 있었다. 몇 가지 일반적인 예는 다음과 같다.

• norm$x\mathbf{}$ $\Vert {}_{}$ $p_{}$ $:=$ $\sum \text{exception 25:}$ $\text{exception 25:}$= $\text{exception 25:}$ $\text{exception 25:}$ i $\sqrt[]{{}^{}}$ p ${\$\$\{p:$$={\sqrt[{p}]{\sum _{i=1}^{n} x_{i}^{p}}}$ $모든{\displaystyle \mathbf{}}$ x${\displaystyle }$∈ ${\displaystyle {}^{}}$ ${\$에 대해 p ${\displaysty p}$는 양의$$ 정수임. 사례 $p{\displaystyle }$= ${\displaystyle 2}$ ${\displaystyle p=2}$는 유클리드 규범이기 때문에 매우 중요하다$$.
• the ${\displaystyle \infty }$-norm or maximum norm, defined by ${\displaystyle \ \mathbf {x} \ _{\infty }:=\max\{x_{1},\dots ,x_{n}\}}$ for all ${\displaystyle {\textbf {x}}\in }$ Rⁿ. This is the limit of all the p-norms: ${\textstyle \ \mathbf {x} \ _{\infty }=\lim _{p\to \infty }{\sqrt[{p}]{\sum _{i=1}^{n} x_{i} ^{p}}}}$.

정말 놀랍고 도움이 되는 결과는ⁿ R에 정의된 모든 규범이 동등하다는 것이다. 즉, R에서ⁿ ${\displaystyle \Vert }$ ${\displaystyle \cdot }$ {$\$ \$cdot$ \$cdot \}과$and$$ $\Vert {\displaystyle }$ ${\displaystyle \Vert }$ ${\displaystyle {}^{}}$ ${\displaystyle {\{}^{}}$ { {$${ { $\cdot \'}}$에 대해 항상 양의 실수 ,> ${\displaysty \alpha ,\beta >0}$을 찾을 수 있다

${\displaystyle \alpha \cdot \ \mathbf {x} \ \leq \ \mathbf {x} \ '\leq \beta \cdot \ \mathbf {x} \ }$ for all ${\displaystyle {\textbf {x}}\in \mathbb {R} ^{n}}$.

이것은 R의ⁿ 모든 규범 집합에 대한 동등성 관계를 정의한다. 이 결과를 통해 R의ⁿ 벡터 시퀀스가${\displaystyle }$‖ { ${\displaystyle \Vert }$‖ {\$displaystyle \cdot$\ \cdot \$$$}$과(와) 수렴되는 경우에만$$ ‖ . . { {${\displaystyle {}^{}}${ { { { $\$과(으)로 수렴되는지 확인할 수 있다$.$

이 결과의 증거가 어떻게 보일 수 있는지에 대한 밑그림은 다음과 같다.

동등성 관계 때문에 R의ⁿ 모든 규범이 유클리드 ${\displaystyle {규범\mathrm{}}_{}}$ ${\displaystyle \Vert }$ ${\displaystyle {}_{}}$ ‖$$2 {\$displaystyle \cdot \_{$2}}.$${ { ${\displaystyle \{}$ $\$ {\$displaystyle \cdot$\}}이ⁿ(가) R의 임의 규범과 동등하다는 것을 보여주기에 충분하다. 증거는 두 단계로 나뉜다.

• 우리는 β 을이 존재한다;0{\displaystyle \beta>0}, ‖)‖≤β ⋅ ‖)‖ 2{\displaystyle)\mathbf{)})\leq \beta \cdot)\mathbf{)}\와 같이 _{2}}모든 x에 ∈ Rn{\displaystyle{\textbf{)}}}. 이 단계에서 여러분은 모든 x=를 사용한다\mathbb{R}^{n}\in(x1,…,)n.을 보여 주 )∈${\displaystyle {\textbf {x}}=(x_{1},\dots ,x_{n})\in \mathbb {R} ^{n}}$ can be represented as a linear combination of the standard basis: ${\textstyle \mathbf {x} =\sum _{i=1}^{n}e_{i}\cdot x_{i}}$. Then with the Cauchy–Schwarz inequality ${\displaystyle \ \mathbf {x} \ =\left\ \sum _{i=1}^{n}e_{i}\cdot x_{i}\right\ \leq \sum _{i=1}^{n}\$$e_{i}\ \cdot x_{i} \leq {\sqrt {\sum _{i=1}^{n}\ e_{i}\ ^{2}}}\cdot {\sqrt {\sum _{i=1}^{n} x_{i} ^{2}}}=\beta \cdot \ \mathbf {x} \ _{2}}$, where ${\displaystyle \beta :={\sqrt {\sum _{i=1}^{n}\ e_{i}\ ^{2}}}}$.
• 이제 우리는α 을을 확인하는 0{\displaystyle \alpha>0},α ⋅ ‖)‖ 2≤ ‖ 모든 x∈ Rn{\displaystyle{\textbf{)}에)‖{\displaystyle \alpha \cdot)\mathbf{)}\와 같이 _{2}\leq)\mathbf{)}\와 같이}}}\mathbb{R}^{n}\in. 가정하라 그런 게 없α{\displaystyle \alpha}은. 그럼 f가 존재하다또는 eve챙겨k∈ N{\displaystylek\in \mathbb{N}}는 xk∈ Rn{\displaystyle \mathbf{)}_{k}\in\mathbb{R}^{n}}, ‖)k‖ 2>k ⋅ ‖)k‖{\displaystyle)\mathbf{)}_{k}\ _{2}>, k\cdot)\mathbf{)}_{k}\}. 정의 두번째 순서()일 k)k∈ N{\displaysty.({르)$tilde {\textbf {{x}}_{k}}_{k\in \mathb{N}}}}$x$$~$k_{}$ : x ~ k${\stackrel{}{}}_{}$:=$x\frac{{\mathbf{}}_{}}{}$ k $\frac{{}_{}}{}$ $\frac{{}_{}}{}$ $\frac{{}_{}{}_{}}{}$ $\frac{{2\mathrm{}}_{}}{}$ ${\${x$}}}}{k}:$$={\frac {\mathbf {x} _{k}{k$}{k$\}\backslash \{$$2}}.$ ${\displaystyle {\stackrel{}{\mathbf{}}}_{}}$ 시퀀스는 $\Vert {\displaystyle }$ x${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle {k\mathrm{}}_{}}$ ${\displaystyle {}_{}{}_{}}$ ${\displaystyle 2{}_{}}$= 1 ${\displaystyle \{\tilde {\mathbf {x}}}}}}{k}\{2}=1$}. 그래서 볼자노– 때문에 경계된다$.$Weierstrass 정리에는 수렴성${\displaystyle {\stackrel{}{}}_{\stackrel{}{}}}$ ~ ${\displaystyle {k_{}}_{}{}_j}$ ) ${\displaystyle {j\mathbb{}}_{}}${\$displaystyle({\tilde{x}}_{k_{j})_{j\in \mathb{N}}}}}}$이(가$)$ 있으며${\displaystyle ,}$ $제한$은 ${\displaystystyle {\textb{a}$이다ⁿ. 이제 ${\displaystyle \Vert {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$= ${\displaystyle 1}$ ${\displaystyle \mathbf {a} \{2}=1}을($를) 보여주지만$$ $a{\displaystyle }$= ${\displaystyle 0}$ ${\$은(는) 모순이다. It is ${\displaystyle \ \mathbf {a} \ \leq \left\ \mathbf {a} -{\tilde {\mathbf {x} }}_{k_{j}}\right\ +\left\ {\tilde {\mathbf {x} }}_{k_{$$j}}\right\ \leq \beta \cdot \left\ \mathbf {a} -{\tilde {\mathbf {x} }}_{k_{j}}\right\ _{2}+{\frac {\ \mathbf {x} _{k_{j}}\ }{\ \mathbf {x} _{k_{j}}\ _{2}}}\ {\overset {j\to \infty }{\to }}\ 0}$, because ${\displaystyle \ \mathbf {a} -{\tilde {\mathbf {x} }}_{k_{j}}\ \to 0}$ and ${\displaystyle 0\leq {\frac {\ \mathbf {x} _{k_{j}}\ }{\ \mathbf {x} _{k_{j}}\ _{2}}}<{\frac {1}{k_{j}}}}$, so ${\displaystyle {\frac {\ {\textbf {x}}_{k_{j}}\ }{\ \mathbf {x} _{k_{j}}\ _{2}}}\to 0}$. This implies ${\displaystyle \ \mathbf {a} \ =0}$, so ${\displaystyle {\textbf {a}}={\textbf {0}}}$. On the other hand ${\displaystyle \ \mathbf {a} \ _{2}=1}$, because ${\displaystyle \Vert \mathbf{a}{\Vert }_2={\Vert \underset{j\to \mathrm{\infty }}{lim}{\widetilde{\mathbf{\text{x}}}}_{k_j}\Vert }_2=\underset{j\to \mathrm{\infty }}{lim}{\Vert {\widetilde{\mathbf{\text{x}}}}_{k_j}\Vert }_{}}$${\displaystyle \ \mathbf {a} \ _{2}=\left\ \lim _{j\to \infty }{\tilde {\textbf {x}}}_{k_{j}}\right\ _{2}=\lim _{j\to \infty }\left\ {\tilde {\textbf {x}}}_{k_{j}}\right\ _{2}=1}$. 이것은 결코 진실일 수 없기 때문에 가정은 거짓이었고 그러한 > $[\displaystyle \alpha >0}$이 존재했다

참고 항목

• 지수 객체, 위첨자 표기법 이론적 설명
• 실제 투영 공간

각주

참조

• Kelley, John L. (1975). General Topology. Springer-Verlag. ISBN 0-387-90125-6.
• Munkres, James (1999). Topology. Prentice-Hall. ISBN 0-13-181629-2.