고유값 및 고유 벡터

선형대수학에서, 선형 변환의 고유벡터(/aaɡənˌvktktrr/) 또는 특성벡터는 그 선형 변환이 적용되었을 때 스칼라 인수에 의해 기껏해야 변하는 0이 아닌 벡터다.$흔히{\displaystyle }$ value ${\displaystyle \lambda$}로 표시되는 해당 고유값은 고유 벡터가 스케일링되는 요인이다$.$

기하학적으로, 실제 0이 아닌 고유값에 해당하는 고유 벡터는 변환에 의해 확장되는 방향을 가리키며 고유값은 그것이 늘어나는 요인이다.고유값이 음수일 경우 방향이 반전된다.^[1]느슨하게 말하면 다차원 벡터 공간에서는 고유벡터가 회전하지 않는다.

형식 정의

T가 필드 F를 통한 벡터 공간 V에서 그 자체로 선형 변환이고 V가 V에서 0이 아닌 벡터인 경우, T(v)가 V의 스칼라 배수인 경우 V는 T의 고유 벡터다.라고 쓸 수 있다.

여기서 λ은 고유값, 특성값 또는 v와 관련된 특성 루트로 알려진 F의 스칼라이다.

n-by-n 제곱 행렬과 n-차원 벡터 공간에서 그 자체로 선형 변환 사이에는 직접적인 일치성이 있다.따라서 유한 차원 벡터 공간에서는 행렬의 언어 또는 선형 변환의 언어를 사용하여 고유값과 고유 벡터를 정의하는 것과 동등하다.^[2][3]

V가 유한 차원일 경우 위의 방정식은 다음과 같다^[4].

여기서 A는 T의 행렬표현이고 u는 v의 좌표 벡터다.

개요

고유값과 고유 벡터는 선형 변환 분석에서 두드러지게 특징지어진다.고유어 접두사는 "property", "propertic", "소유"^[5][6]에 대해 독일어 고유어(영어 단어 자체와 인식)에서 채택된다.원래 강체 회전운동의 주축을 연구하기 위해 사용되던 고유값과 고유벡터는 안정성 분석, 진동분석, 원자궤도, 안면인식, 매트릭스 대각화 등 응용 범위가 넓다.

본질적으로, 선형 변환 T의 고유 벡터 v는 T를 적용했을 때 방향이 변하지 않는 0이 아닌 벡터다.고유 벡터에 T를 적용하면 고유값이라고 하는 스칼라 값 λ에 의해서만 고유 벡터의 스케일이 조정된다.이 조건은 방정식으로 쓸 수 있다.

고유값 방정식 또는 아이게네쿼팅이라고 한다.일반적으로 λ은 어떤 스칼라일 수도 있다.예를 들어 λ은 음수일 수 있으며, 이 경우 고유벡터는 스케일링의 일부로 방향을 반전시키거나 0이거나 복잡할 수 있다.

여기에 묘사된 모나리자 예는 간단한 예시를 제공한다.그림의 각 점은 그림의 중심에서 그 지점까지 가리키는 벡터로 나타낼 수 있다.이 예에서 선형 변환을 전단 매핑이라고 한다.그림의 중간을 통과하는 수평축으로부터 얼마나 멀리 떨어져 있는가에 비례하여 상반부의 점들은 오른쪽으로 이동하고, 하반부의 점들은 왼쪽으로 이동한다.따라서 원본 영상에서 각 지점을 가리키는 벡터는 오른쪽 또는 왼쪽으로 기울어져 있으며 변환에 의해 더 길거나 짧게 된다.이 변환을 적용할 때 수평 축을 따라 있는 점은 전혀 움직이지 않는다.따라서 수직 구성요소가 없는 오른쪽이나 왼쪽으로 직접 가리키는 벡터는 매핑의 방향이 바뀌지 않기 때문에 이 변환의 고유 벡터가 된다.더욱이 이러한 고유 벡터들은 모두 1과 동일한 고유값을 가지고 있다. 왜냐하면 매핑 역시 길이를 변경하지 않기 때문이다.

선형 변환은 다양한 벡터 공간에 벡터를 매핑하여 여러 가지 형태를 취할 수 있으므로 고유 벡터도 여러 형태를 취할 수 있다.예를 들어, 선형 변환은 $d{\displaystyle \frac{}{}}$ ${\displaystyle \frac{d}{}}$ x ${\$과 같은 차동 연산자가 될 수 있으며$,$ 이 경우 고유 벡터는 다음과 같이 차동 연산자에 의해 스케일링되는 고유 기능이라고 한다.

또는 선형 변환은 n by n 행렬의 형태를 취할 수 있으며, 이 경우 고유 벡터는 n by 1 행렬이다.선형 변환을 n행렬 A로 표현하면 위의 선형 변환에 대한 고유값 방정식을 행렬 곱셈으로 다시 쓸 수 있다.

여기서 고유 벡터 v는 n X 1 행렬이다.행렬의 경우 고유값과 고유 벡터를 사용하여 행렬을 분해할 수 있다(예: 대각선으로).

고유값과 고유 벡터는 밀접하게 연관된 많은 수학 개념을 발생시키며, 다음과 같은 이름을 붙일 때 접두사 고유(eigen-)가 자유자재로 적용된다.

• 선형 변환의 모든 고유 벡터 집합을 해당 고유값과 쌍을 이루며, 이 변환의 고유 벡터 집합을 해당 변환의 eigensystem이라고 한다.^[7][8]
• 동일한 고유값에 해당하는 T의 모든 고유 벡터 세트를 영 벡터와 함께 아이겐스페이스 또는 그 고유값과 연관된 T의 특성 공간이라고 한다.^[9]
• T의 고유 벡터 집합이 T의 영역의 기초를 형성하는 경우, 이 기준을 고유바시스라고 한다.

역사

고유값은 선형대수학이나 행렬이론의 맥락에서 도입되는 경우가 많다.그러나 역사적으로 그들은 이차적 형태와 미분 방정식을 연구하는 과정에서 생겨났다.

18세기에 레온하르트 오일러는 강체의 회전 운동을 연구하여 주축의 중요성을 발견하였다.^[a]Joseph-Louis Lagrange는 주요 축이 관성 행렬의 고유 벡터라는 것을 깨달았다.^[10]

19세기 초 아우구스틴루이 카우치는 그들의 작업이 어떻게 4중 표면을 분류하는 데 사용될 수 있는지를 보고 그것을 임의의 차원으로 일반화했다.^[11]코치는 또한 현재 고유값이라고 불리는 것을 위해 라신 카락테리스티크(성격근)라는 용어를 만들었다. 그의 용어는 특성 방정식에서 살아남는다.^[b]

이후 조셉 푸리에가 라그랑주와 피에르시몬 라플레이스의 작품을 이용해 그의 유명한 1822년 저서 테오리 분석기 데 라 샤를루르에서 변수의 분리에 의한 열 방정식을 풀었다.^[12]샤를-프랑수아 스투름은 푸리에의 사상을 더욱 발전시켜 카우치(Cauchy)의 주목을 받게 하였는데, 카우치(Cauchy)는 이를 자신의 사상과 결합시켜 실제 대칭 행렬이 실제 고유값을 갖는다는 사실에 도달했다.^[11]이것은 1855년 찰스 헤르미테에 의해 현재 에르미트 행렬로 확장되었다.^[13]

비슷한 시기에 프란체스코 브리오슈는 직교 행렬의 고유값이 단위 원 위에 있음을 증명했고,^[11] 알프레드 클레브슈는 스큐 대칭 행렬에 대한 해당 결과를 찾아냈다.^[13]마지막으로 칼 위어스트라스는 결함이 있는 행렬이 불안정성을 야기할 수 있다는 것을 깨달음으로써 라플레이스가 시작한 안정성 이론에서 중요한 측면을 명확히 했다.^[11]

그 동안 조셉 리우빌은 스터름과 비슷한 고유 가치 문제를 연구했다; 그들의 일에서 자라난 규율을 이제는 스터름-리우빌 이론이라고 부른다.^[14]슈바르츠는 19세기 말경 일반영역에 대한 라플레이스의 방정식의 첫 고유치를 연구했고, 푸앵카레는 몇 년 후 포아송의 방정식을 연구했다.^[15]

20세기 초에 데이비드 힐버트는 연산자를 무한 행렬로 보고 적분 연산자의 고유값을 연구했다.^[16]그는 헤르만 폰 헬름홀츠에 의해 관련 용법을 따르고 있었는지도 모르지만 1904년에 "소유"^[6]를 의미하는 독일어 고유값과 고유벡터를 최초로 사용했다.^[c]한동안 영어의 표준어는 '적재적 가치'였지만, 오늘날에는 '유전자 가치'라는 독특한 용어가 표준이다.^[17]

고유값과 고유벡터 계산을 위한 첫 번째 수치 알고리즘은 1929년 리처드 폰 미제스가 동력법을 발표하면서 나타났다.오늘날 가장 인기 있는 방법 중 하나인 QR 알고리즘은 1961년 존 G. F. 프랜시스와^[18] 베라 쿠블라노프스카야에^[19] 의해 독립적으로 제안되었다.^[20][21]

행렬의 고유값 및 고유 벡터

고유값과 고유 벡터는 행렬에 초점을 맞춘 선형 대수 과정의 맥락에서 학생들에게 종종 소개된다.^[22][23]또한 유한차원 벡터 공간에 대한 선형 변환은 행렬을 사용하여 나타낼 수 있으며,^[2][3] 이는 특히 수치적 및 계산적 애플리케이션에서 일반적이다.^[24]

3차원 벡터와 같이 n개의 스칼라 목록으로 형성된 n차원 벡터를 고려한다.

이러한 벡터는 서로 스칼라 배수로 되어 있거나, 만일 스칼라 λ이 있으면 평행 또는 콜린어라고 한다.

이 경우 $\lambda {\displaystyle }$=${\displaystyle }$- 1 ${\displaystyle \frac{20}{}}$ ${\$.

이제 n by n 행렬 A로 정의된 n차원 벡터의 선형 변환을 고려한다.

또는

각 행에 대해

v와 w가 스칼라 배수인 경우, 즉

${\displaystyle A\mathbf {v} =\mathbf {w} =\lambda \mathbf {v},}$

(1)

그 다음 v는 선형 변환 A의 고유 벡터이고 척도 계수 λ은 해당 고유 벡터에 해당하는 고유값이다.방정식 (1)은 행렬 A의 고유값 방정식이다.

식 (1)은 다음과 같이 동등하게 표현될 수 있다.

${\displaystyle \left(A-\lambda I\right)\mathbf {v} =\mathbf {0},}$

(2)

여기서 나는 n by n ID 행렬이고 0은 0 벡터다.

고유값과 특성 다항식

등식 (2)는 행렬의 결정인자(A - determinI)가 0인 경우에만 0이 아닌 용액 v를 갖는다.따라서 A의 고유값은 방정식을 만족시키는 λ의 값이다.

$[\displaystyle A-\lambda I =0}$

(3)

결정인자에 라이프니츠의 규칙을 이용하여 등식 (3)의 왼쪽은 변수 λ의 다항식 함수로서 이 다항식의 정도는 행렬 A의 순서인 n이다.계수는 A의 입력에 따라 달라지는데, 단, 도 n의 항은 항상 (-1)ⁿλ이다ⁿ.이 다항식을 A의 특성 다항식이라고 한다.방정식 (3)을 A의 특성 방정식 또는 세속 방정식이라고 한다.

대수학의 기본 정리는 n-by-n 행렬 A의 특성 다항식이 n의 다항식인 것을 의미하며, n의 선형 항들의 곱으로 인수될 수 있다.

${\displaystyle A-\lambda I =(\lambda _{1}-\lambda )(\lambda _{2}-\lambda )\cdots(\lambda _{n}-\lambda ),}$

(4)

여기서 각_i each은 실제일 수 있으나 일반적으로 복잡한 숫자다.모두 뚜렷한 값을 가지지 않을 수도 있는 숫자 λ₁, λ₂, …, λ은_n 다항식의 뿌리로서 A의 고유값이다.

간단한 예로서, 나중에 예제 섹션에 자세히 설명되어 있으므로 행렬을 고려하십시오.

(A - λI)의 결정요인을 취하면 A의 특성 다항식은

특성 다항식을 0으로 설정하면 A의 두 고유값인 λ=1과 λ=3에 뿌리를 두고 있다.각 고유값에 해당하는 고유 벡터는 방정식$({\displaystyle A}$ -${\displaystyle \lambda }$ I${\displaystyle }$) v${\displaystyle }$= ${\displaystyle 0\mathbf{}}$ ${\$에서 v의 성분을 풀어서 찾을 수 있다$.$ 이 예에서 고유 벡터는 0이 아닌 스칼라 배이다.

행렬 A의 항목이 모두 실제 숫자일 경우 특성 다항식의 계수도 실제 숫자가 되지만 고유값은 여전히 0이 아닌 가상 부품을 가질 수 있다.따라서 해당 고유 벡터의 항목도 0이 아닌 가상 부품을 가질 수 있다.마찬가지로 고유값은 A의 모든 항목이 합리적 숫자라거나 모두 정수라 하더라도 비합리적인 숫자일 수 있다.그러나 A의 항목이 모두 이성계를 포함하는 대수적 숫자라면 고유값은 복잡한 대수적 숫자다.

실제 계수가 있는 실제 다항식의 비현실적 루트는 복잡한 결합체의 쌍으로 그룹화할 수 있으며, 즉 각 쌍의 두 구성원이 부호와 동일한 실제 부분만 다른 가상의 부품을 가지고 있다.만약 정도가 홀수라면, 중간값 정리에 의해 적어도 하나의 뿌리가 실재한다.따라서 순서가 홀수인 실제 행렬은 최소 하나의 실제 고유값을 갖는 반면, 짝수인 실제 행렬은 실제 고유값을 갖지 못할 수 있다.이러한 복잡한 고유값과 연관된 고유 벡터 또한 복잡하며 복잡한 결합 쌍에서도 나타난다.

대수적 다중성

λ은_i n by n 행렬 A의 고유값이 되도록 한다.고유치의 대수적 다항성 μ_A(μ_i)는 특성 다항식의 루트로서 그 다중성, 즉 ( ( - λ_i)^k이 그 다항식을 고르게 나누는 가장 큰 정수 k이다.^[9][25][26]

행렬 A에 차원 n과 d ≤ 구별되는 고유값이 있다고 가정합시다.방정식 (4)이 A의 특성 다항식을 잠재적으로 반복되는 n개의 선형 항의 곱으로 인하는 반면에, 특성 다항식은 대신 고유한 고유값에 해당하는 d 항의 곱으로 기록하고 대수적 다항성으로 올릴 수 있다.

d = n이면 우측은 n개의 선형 항의 산물이고 이는 방정식 (4)과 동일하다.각 고유값의 대수적 다중의 크기는 다음과 같은 차원 n과 관련이 있다.

μ_A(μ_i) = 1이면 μ는_i 단순한 고유값이라고 한다.^[26]만약_A μ(μ_i)가 다음 절에서 정의한 λ_iA, ((λ_i)의 기하학적 다중성과 동일하다면, λ은_i 반이 구현된 고유값이라고 한다.

Eigenspaces, 기하학적 다중성 및 행렬의 고유 기준

n by n 행렬 A에 의한 n의 특정 고유값 λ이 주어진 경우, E를 방정식 (2)를 만족하는 모든 벡터 v로 정의한다.

한편, 이 세트는 정확히 매트릭스의 커널 또는 널스페이스(A - λI)이다.한편, 정의상 이 조건을 만족하는 비제로 벡터는 모두 λ과 연관된 A의 고유 벡터로서, set E는 with과 연관된 A의 모든 고유 벡터 집합과 제로 벡터의 결합이며, E는 (A - iI)의 nullspace와 같다.E는 λ과 연관된 A의 Eigenspace 또는 특성공간이라고 불린다.^[27][9]일반적으로 λ은 복잡한 수이고 고유 벡터는 복잡 n X 1 행렬이다.nullspace의 속성은 선형 하위공간이므로 E는 ℂ의ⁿ 선형 하위공간이다.

Eigenspace E는 선형 하위 공간이기 때문에 추가 시 닫힌다.즉, 두 벡터 u와 v가 설정된 E에 속하면 u, v ∈ E, (u + v) ∈ E 또는 동등하게 A(u + v) = =(u + v)이다.이것은 매트릭스 곱셈의 분포 특성을 이용하여 확인할 수 있다.마찬가지로 E는 선형 아공간이기 때문에 스칼라 곱셈에 의해 닫힌다.즉, v ∈ E와 α가 복합수일 경우 (αv) e E 또는 동등하게 A(αv) = λ(αv)이다.이것은 복잡한 행렬을 복잡한 숫자로 곱하는 것이 상쇄적이라는 것을 알아봄으로써 확인할 수 있다.u + v와 αv가 0이 아닌 한 λ과 연관된 A의 고유 벡터이기도 하다.

λ과 연관된 eigenspace E의 치수, 또는 ently과 연관된 선형 독립 고유 벡터의 최대 개수를 동등하게 고유값의 기하학적 다중성 γ_A(λ)이라고 한다.E는 (A - λI)의 nullspace이기도 하기 때문에, -의 기하학적 다중성은 (A - dimensionI)의 nullspace 치수로서 (A - λI)의 nullity라고도 하는데, 이는 (A - λI)의 치수 및 순위와도 관련이 있다.

고유값과 고유벡터의 정의 때문에 고유값의 기하학적 다중성은 적어도 하나 이상이어야 한다. 즉, 각 고유값에는 적어도 하나 이상의 관련 고유벡터가 있어야 한다.또한 고유값의 기하학적 다중성은 대수적 다중성을 초과할 수 없다.또한 고유값의 대수적 다중성은 n을 초과할 수 없다는 점을 상기한다.

To prove the inequality ${\displaystyle \gamma _{A}(\lambda )\leq \mu _{A}(\lambda )}$, consider how the definition of geometric multiplicity implies the existence of ${\displaystyle \gamma _{A}(\lambda )}$ orthonormal eigenvectors ${\displaystyle {$$\boldsymbol {v}}_{1},\,\ldots ,\,{\boldsymbol {v}}_{\gamma _{A}(\lambda )}}$, such that ${\displaystyle A{\boldsymbol {v}}_{k}=\lambda {\boldsymbol {v}}_{k}}$. We can therefore find a (unitary) matrix ${\displaystyle V}$ whose first ${\displaystyle \gamma _{A}(\lambda )}$ columns are these eigenvectors, and whose remaining columns can be any orthonormal set of ${\displaystyle n-\gamma _{A}(\lambda )}$ vectors orthogonal to these eigenvectors of ${\displaystyle A}$. Then ${\displaystyle V}$ has full rank and is therefore invertible, and ${\displaystyle AV=VD}$ with ${\di$$splaystyle D}$ a matrix whose top left block is the diagonal matrix ${\displaystyle \lambda I_{\gamma _{A}(\lambda )}}$. This implies that ${\displaystyle (A-\xi I)V=V(D-\xi I)}$. In other words, ${\displaystyle A-\xi I}$ is similar to ${\displaystyle D-\xi$$I}$, which implies that ${\displaystyle \det(A-\xi I)=\det(D-\xi I)}$. But from the definition of ${\displaystyle D}$ we know that ${\displaystyle \det(D-\xi I)}$ contains a factor ${\displaystyle (\xi -\lambda )^{\gamma _{A}(\lambda )}}$, which$multipl{\displaystyle }$ ${\displaystyle \lambda }$의 대수적 곱셈이 ${\displaystyle {\mu A}_{}}$ ${\displaystyle {}_{}\lambda }$) ${\displaystyle \ge }$ ${\displaystyle {}_{}}$(${\displaystyle \lambda }$ ${\displaystyle )}$ ${\displaystyle \mu _{A}(\lambda )\geq \gamma _{A}(\lambda )}$을 만족해야$$ 함을 의미한다$.$

Suppose ${\displaystyle A}$ has ${\displaystyle d\leq n}$ distinct eigenvalues ${\displaystyle \lambda _{1},\ldots ,\lambda _{d}}$, where the geometric multiplicity of ${\displaystyle \lambda _{i}}$ is ${\displaystyle \gamma _{A}(\lambda _{i})}$.$A{\displaystyle }$ ${\displaystyle A}$의 총 기하학적 다중성$,$

$A{\displaystyle }$ ${\displaystyle A}$의$$고유값 또는 A ${\displaystyle A}$의 선형 독립 고유 벡터 최대 개수의 모든 아이겐스페이스의 합계 치수$.$ 만약 $\gamma {\displaystyle {}_{}}$ ${\displaystyle A_{}}$= ${\displaystyle n}$ ${\displaystyle \gamma _{A}=n$ 그렇다면

• $모든{\displaystyle }$ A ${\displaystyle A}$의$$고유값의 아이겐스페이스의 직접 합은 전체 벡터 공간 $C{\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {}^{}}$ ${\$이다$.$
• $C{\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {}^{}}$ ${\$$$$^{n}$의 기초는 $A{\displaystyle }$ ${\displaystyle A}$의 $선형{\displaystyle }$ 독립 고유 벡터로부터 형성될$$ 수 있다$.$ 이러한 기초를 고유베이스라고 한다.
• ${\displaystyle {}^{}}$ ${\$의 벡터는 $A{\displaystyle }$ ${\displaystyle A}$의 고유 벡터의 선형 결합으로 기록할 수 있다$$$.$

고유값의 추가 특성

Let ${\displaystyle A}$ be an arbitrary ${\displaystyle n\times n}$ matrix of complex numbers with eigenvalues ${\displaystyle \lambda _{1},\ldots ,\lambda _{n}}$. Each eigenvalue appears ${\displaystyle \mu _{A}(\lambda _{i})}$ times in this list, where ${\displaystyle {\mu }_A({\lambda }_i}$${\displaystyle )}$ ${\displaystyle \mu _{A}(\lambda _{i})$는 고유값의 대수적 곱이다.다음은 이 행렬과 그 고유값의 속성이다.

• 대각선 원소의 합으로 정의된 $A$${\displaystyle A}$의 추적은 모든 고유값의 합이기도 하다.^[28][29][30]

  ${\displaystyle \operatorname {tr}(A)=\sum _{i=1}^{n}a_{i}=\sum _{i=1}^{n}\lambda _{1}+\lambda _{2}+\lambda _\lambda _{n}.}$

• $A{\displaystyle }$ ${\displaystyle A}$의 결정 요소는 모든$$ 고유값의 산물이다.^[28][31][32]

  $\displaystyle \det(A)=\prod _{i=1}^{n}\lambda _{1}=\lambda _{1}\lambda _{2}\cdots \lambda _{n}.}$

• The eigenvalues of the ${\displaystyle k}$^th power of ${\displaystyle A}$; i.e., the eigenvalues of ${\displaystyle A^{k}}$, for any positive integer ${\displaystyle k}$, are ${\displaystyle \lambda _{1}^{k},\ldots ,\lambda _{n}^{k}}$.
• 모든 고유값이 0이 아닌 경우에만 $행렬{\displaystyle }$ A {\$displaystyle A}$을(를$)$ 변환할 수 있다.
• If ${\displaystyle A}$ is invertible, then the eigenvalues of ${\displaystyle A^{-1}}$ are ${\textstyle {\frac {1}{\lambda _{1}}},\ldots ,{\frac {1}{\lambda _{n}}}}$ and each eigenvalue's geometric multiplicity coincides.더욱이 역의 특성 다항식이 원전의 역수 다항식이기 때문에 고유값은 같은 대수적 다항성을 공유한다.
• $만약{\displaystyle }$ A ${\displaystyle A}$이(가) 결합 전치 $A{\displaystyle {}^{}}$∗ ${\$ A$^{*}$와 같거나$$$,$ $A{\displaystyle }$ ${\displaystyle A}$이(가) 에르미타인 경우 모든 고유값이 실제 값이다.대칭 실제 행렬도 마찬가지다.
• $만일{\displaystyle }$ A ${\displaystyle A}$이(가) 에르미타인뿐만 아니라 양정확성, 양정확성, 음정확률, 음정확률 또는 음정확률이라면 모든 고유값은 각각 양, 비음, 음 또는 양이다.
• $A{\displaystyle }$ ${\displaystyle A}$이(가) 단일인 경우 모든 고유값은 ${\displaystyle {절대값}_{}}$ ∆ ${\displaystyle i{}_{}{}_{}}$= ${\displaystyle 1}$ ${\displaystyle \lambda _{i} =1}$을(를) 갖는다$.$
• if ${\displaystyle A}$ is a ${\displaystyle n\times n}$ matrix and ${\displaystyle \{\lambda _{1},\ldots ,\lambda _{k}\}}$ are its eigenvalues, then the eigenvalues of matrix ${\displaystyle I+A}$ (where ${\displaystyle I}$ is the identity matrix) are ${\displaystyle \{{\lambda }_1+1,\dots ,{\lambda }_{}}$${\displaystyle \{\lambda _{1}+1,\ldots ,\lambda _{k}+1\}}$. Moreover, if ${\displaystyle \alpha \in \mathbb {C} }$, the eigenvalues of ${\displaystyle \alpha I+A}$ are ${\displaystyle \{\lambda _{1}+\alpha ,\ldots ,\lambda _{k}+\alpha \}}$. More generally, for a poly$명목{\displaystyle }$ $P{\displaystyle }$ ${\$$displaystyle P}$ 행렬 P$(A)$의 고유값은${\displaystyle }${ ${\displaystyle P{}_{}{A\mathrm{}}_{}}$ )${\displaystyle }$, ${\displaystyle \dots ,}$P${\displaystyle (P_{}}$} ${\displaystyle \{P(\lambda _{1}),\lambda _$$k}\}$입니다.

좌우 고유 벡터

많은 학문들은 전통적으로 벡터를 하나의 행을 가진 행렬이 아니라 하나의 열을 가진 행렬로 표현한다.그러한 이유로 행렬의 맥락에서 "유겐벡터"라는 단어는 거의 항상 우측 고유벡터, ${\displaystyle 즉}$ 정의 방정식 (1)에서 $n{\displaystyle }$ ${\displaystyle \times }$ n ${\displaystyle n\times n}$ 행렬$$ $A{\displaystyle }$ ${\displaystyle A}$를 오른쪽으로 곱하는 열 벡터를 가리킨다.

고유값과 고유벡터 문제는 또한 왼쪽 곱셈 $행렬{\displaystyle }$ A ${\displaystyle A}$ 행 벡터에 대해 정의될 수 있다$.$ 이 공식에서 정의 방정식은 다음과 같다.

여기서 $\kappa {\displaystyle }$ ${\displaystyle \kappa }$은(는) 스칼라이고 $u{\displaystyle }$ ${\displaystyle u}$은(는) $1{\displaystyle \mathrm{}}$ ${\displaystyle \times }$ ${\displaystyle n}$ ${\displaystyle 1\put n}$ 행렬이다$$.이 방정식을 만족하는$$ 모든 행 벡터 $u{\displaystyle }$ ${\$$displaystyle u}$을(를) $A$의 왼쪽 고유 벡터라고 하며$$, $\kappa {\displaystyle }$ ${\displaystyle \kappa }$은 연관된$$ 고유값이다.이 방정식의 전치사를 보면

이 방정식을 방정식 (1)과 비교하면, $A{\displaystyle }$ ${\displaystyle A}$의 왼쪽 고유 벡터가 동일한 고유값을 가진 ${\displaystyle A^{}}$ T$${\$displaystyle$ A$^{\textsf {T$의 오른쪽 고유벡터 전치 값과 같다는$$ 것이 바로 뒤따른다.Furthermore, since the characteristic polynomial of ${\displaystyle A^{\textsf {T}}}$ is the same as the characteristic polynomial of ${\displaystyle A}$, the eigenvalues of the left eigenvectors of ${\displaystyle A}$ are the same as the eigenvalues of the right eigenvectors of ${\displaystyle A^{\te$$xtsf {T}}$.

대각화 및 에겐데 구성

A의 고유 벡터가 기초를 형성하거나 동등하게 A가 연관된 고유값 λ₁, λ₂, λ, …와_n 함께 n개의 선형 독립 고유 벡터 v₁, v₂, …, v를_n 가지고 있다고 가정하자.고유값은 구별할 필요가 없다.열이 A의 n 선형 독립 고유 벡터인 정사각형 행렬 Q를 정의한다.

${\displaystyle Q={\begin{bmatrix}\mathbf {v} _{1}&\mathbf {v} _{2}\cdots &\mathbf {v} _{n}\end{bmatrix}}}.}$

Q의 각 열은 A의 고유 벡터이므로, A와 Q를 곱한 오른쪽 열은 관련된 고유값을 기준으로 Q의 각 열을 척도한다.

${\displaystyle AQ={\begin{bmatrix}\lambda _{1}\mathbf {v} _{1}&\lambda _{2}\cdots &\lambda _{n}\mathbf {v}\end{bmatrix}.}$

이를 염두에 두고 대각 행렬 λ을 정의하십시오. 여기서 각 대각선 원소 λ은_ii Q의 ih 열과 관련된 고유값이다.그러면

$AQ=Q\Lambda.}$

Q의 열은 선형적으로 독립적이기 때문에 Q는 변위할 수 없다.방정식의 양쪽 면에⁻¹ Q를 곱하면

${\displaystyle A=Q\Lambda Q^{1},}$

또는 대신에 왼쪽으로 양쪽에 Q를⁻¹ 곱하면,

${\displaystyle Q^{-1}AQ=\Lambda.}$

따라서 A는 고유 벡터로 구성된 행렬, 대각선을 따라 고유값을 갖는 대각 행렬, 고유 벡터의 행렬의 역행렬로 분해될 수 있다.이것을 에겐데 구성이라고 하며 유사성 변환이다.이러한 행렬 A는 대각 행렬 matrix과 비슷하거나 대각선이 가능하다고 한다.행렬 Q는 유사성 변환의 기본 행렬의 변경이다.본질적으로 행렬 A와 λ은 두 개의 다른 기준으로 표현된 동일한 선형 변환을 나타낸다.고유 벡터는 선형 변환을 λ으로 나타낼 때 기준으로 사용된다.

반대로 행렬 A가 대각선으로 가능하다고 가정합시다.PAP가⁻¹ 대각 행렬 D가 되도록 P를 비노래적 정사각 행렬로 두자.좌측에 P, AP = PD를 곱한 값.따라서 P의 각 열은 고유값이 D의 해당 대각선 요소인 A의 고유 벡터가 되어야 한다.P의 기둥이 변위가 가능하려면 P의 기둥이 선형적으로 독립적이어야 하기 때문에 A의 선형 독립 고유 벡터가 n개 존재한다.그 후 A의 고유 벡터는 A가 대각선으로 가능한 경우에만 기초를 형성한다.

대각선이 가능하지 않은 행렬은 결함이 있다고 한다.결점 행렬의 경우 고유 벡터의 개념은 일반화된 고유 벡터로 일반화되며 고유값의 대각 행렬은 요르단 정규 형태로 일반화된다.대수적으로 폐쇄된 장에 걸쳐 모든 행렬 A는 요르단 정규 형태를 가지며 따라서 일반화된 고유 벡터의 기초와 일반화된 고유 벡터들로 분해되는 것을 허용한다.

가변 특성화

은둔자의 경우 고유값은 변동적 특성을 부여할 수 있다.The largest eigenvalue of ${\displaystyle H}$ is the maximum value of the quadratic form ${\displaystyle \mathbf {x} ^{\textsf {T}}H\mathbf {x} /\mathbf {x} ^{\textsf {T}}\mathbf {x} }$. A value of ${\displaystyle \mathbf {x} }$ that realizes that maximum, is an eigenvector.

행렬 예제

2차원 행렬 예제

행렬 고려

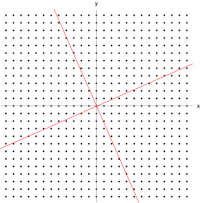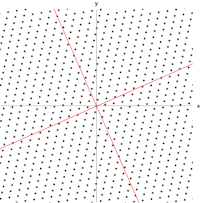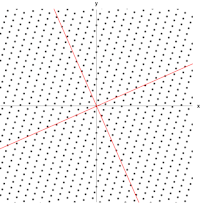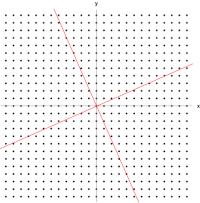
오른쪽 그림은 평면 내 점 좌표에 대한 이 변환의 영향을 보여준다.이 변환의 고유 벡터 v는 방정식 (1)을 만족하며, 행렬의 결정인자(A - λI)가 0과 같은 λ의 값은 고유값이다.

A의 특징적인 다항식을 찾기 위해 결정인자를 택하는 것,

특성 다항식을 0으로 설정하면 A의 두 고유값인 λ=1과 λ=3에 뿌리를 두고 있다.

λ=1, 방정식 (2)는 다음과 같이 된다.

; $1{\displaystyle \mathrm{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$+ ${\displaystyle 1}$ ${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$= ${\displaystyle 0}$ ${\displaystyle 1v_{1}+1v_{2}=0}$

v₁ = -v를₂ 가진 0이 아닌 벡터는 이 방정식을 해결한다.그러므로

이 벡터의 스칼라 배수와 마찬가지로 ctor = 1에 해당하는 A의 고유 벡터다.

λ=3의 경우 방정식 (2)가 된다.

v₁ = v를₂ 가진 0이 아닌 벡터는 이 방정식을 해결한다.그러므로

이 벡터의 스칼라 배수와 마찬가지로 ctor = 3에 해당하는 A의 고유 벡터다.

따라서 벡터 v와_λ=1 v는_λ=3 각각 고유값 λ=1과 λ=3과 연관된 A의 고유 벡터다.

2차원 행렬의 고유값에 대한 일반 공식

실제 행렬 =[ ${\$ A$={\begin{bmatrix}a&b\c&d\end{bmatrix}}$의 고유값은 다음과^[d] 같다.

${\displaystyle \lambda ={\frac {1}{2}}(a+d)\pm {\sqrt {\left({\frac {1}{2}}(a-d)\right)^{2}+bc}}={\frac {1}{2}}\left(\operatorname {tr} (A)\pm {\sqrt {\left(\operatorname {tr} (A)\right)^{2}-4\det(A)}}\right).}$

An alternate representation is: ${\displaystyle \lambda ={\frac {1}{2}}\operatorname {tr} (A)\pm {\sqrt {\left({\frac {1}{2}}\operatorname {tr} (A)\right)^{2}-\det(A)}}.$$}$

급진주의 아래의 수량은 양수여야 하므로 b와 c의 부호가 같을 경우 고유값은 항상 실제 값이라는 점에 유의한다.

3차원 행렬 예제

행렬 고려

A의 특징적인 다항식은

특성 다항식의 뿌리는 A의 유일한 고유값인 2, 1, 11이다.이 eigenvalues은 값[100]T{\displaystyle{\begin{bmatrix}1&amp에;0&, 0\end{bmatrix}}^{\textsf{T}}},[0− 2대 1]T{\displaystyle{\begin{bmatrix}0&, -2&, 1\end{bmatrix}}^{\textsf{T}}},[012]T{{\begin{bma\displaystyle 일치한다.trix}0&, 1&, 2\end{$bmatrix}^{\textsf{T}}$ 또는0이 아닌 배수.

복합 고유값을 갖는 3차원 행렬 예제

순환 순열 행렬 고려

이 행렬은 벡터의 좌표를 한 위치 위로 이동시키고 첫 번째 좌표를 하단으로 이동시킨다.특징적인 다항식은 1 - λ이며³, 그 뿌리는 다음과 같다.

여기서 $i{\displaystyle }$ ${\displaystyle$ i$}$은(는) $i{\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$=${\displaystyle }$- ${\displaystyle 1}$ ${\displaystyle i^{2}=-1}$을(를) 가진 가상 단위다$.$

실제 고유값 λ₁ = 1의 경우, 세 개의 0이 아닌 입력이 동일한 벡터는 모두 고유 벡터가 된다.예를 들어,

상상 고유값의 복잡한 결합 쌍의 경우,

그러면

그리고

따라서, A의 다른 두 값이v λ 2)[1λ 2λ 3]T{\displaystyle \mathbf{v}_{\lambda_{2}}={\begin{bmatrix}1&, \lambda _{2}&, \lambda _{3}\end{bmatrix}}^{\textsf{T}}}, 탭[1λ 3λ 2]T{\displaystyle \mathb λ 3v 복잡하다.f{v}_{$\lambda _{3}}={\begin{bmatrix}1&\lambda _{3}&\lambda _{2}\end{bmatrix}}^{\textsf{T}}}}$는 각각 고유값 λ과₂ and이₃ 있는 것으로 나타났다.두 개의 복잡한 고유 벡터는 복잡한 결합 쌍에서도 나타난다.

대각 행렬 예제

주 대각선을 따라만 입력되는 행렬을 대각 행렬이라고 한다.대각 행렬의 고유값은 대각선 원소 그 자체다.행렬 고려

A의 특징적인 다항식은

뿌리가₁ 1, , = 2, λ₂₃ = 3이다.이러한 뿌리는 A의 고유값뿐만 아니라 대각선 원소들이다.

각 대각선 요소는 0이 아닌 유일한 성분이 대각선 원소와 같은 행에 있는 고유 벡터에 해당한다.이 예에서 고유값은 고유 벡터에 해당한다.

이 벡터의 스칼라 배수와 함께 각각.

삼각 행렬 예제

주 대각선 위의 원소가 모두 0인 행렬을 하위 삼각 행렬이라고 하고, 주 대각선 아래의 원소가 모두 0인 행렬을 상위 삼각 행렬이라고 한다.대각 행렬과 마찬가지로 삼각 행렬의 고유값은 주 대각선의 요소다.

아래 삼각형 행렬을 고려하십시오.

A의 특징적인 다항식은

뿌리가₁ 1, , = 2, λ₂₃ = 3이다.이러한 뿌리는 A의 고유값뿐만 아니라 대각선 원소들이다.

이 고유값은 고유 벡터에 해당하며

이 벡터의 스칼라 배수와 함께 각각.

고유값이 반복되는 행렬 예제

앞의 예와 같이 아래쪽 삼각 행렬

대각선 원소의 산물인 특징적인 다항식을 가지고 있다.

이 다항식의 뿌리와 따라서 고유값은 2와 3이다.각각의 고유값의 대수적 다중성은 2이다. 즉, 그들은 둘 다 이중근이다.모든 구별되는 고유값의 대수적 승수의 합은_A μ = 4 = n, 특성 다항식의 순서와 A의 치수다.

반면 고유값 2의 기하학적 다중성은 1에 불과한데, 그 이유는 그 고유값 2의 eigenspace가 단지 하나의 벡터[ - ${\$에 의해 1차원이기 때문이다.마찬가지로 고유치 3의 기하학적 다수는 1이기 때문에 eigenspace 단지 하나의 벡터[0001]T{\displaystyle{\begin{bmatrix}0&amp에 걸쳐 있었다;0&, 0&, 1\end{bmatrix}}^{\textsf{T}}}. 총 기하학적 다양한 γA 2는 두개의 뚜렷한 ei과 행렬할 수 없을 정도로 작은 행성입니다.genvalues.기하학적 승수는 나중의 섹션에서 정의된다.

고유벡터 고유값 ID

은둔자 행렬의 경우 정규화된 고유 벡터의 j번째 성분의 표준 제곱은 해당 부 행렬의 고유값과 고유값만 사용하여 계산할 수 있다.

여기서 $M{}_{}$ $j_{}$ ${\$는 원래 행렬에서 j번째 행과 열을 제거하여 형성된 하위 행렬이다.^[33][34][35]이 정체성은 또한 대각선으로 가능한 행렬까지 확장되며, 문헌에서 여러 번 재발견되었다.^[34]

미분 연산자의 고유값 및 고유 특성

선형 변환 T의 고유값과 고유 벡터의 정의는 기초 벡터 공간이 무한 차원 힐버트 또는 바나흐 공간이라고 하더라도 유효하다.무한 차원 공간에 작용하는 선형 변환의 널리 사용되는 클래스는 함수 공간의 미분 연산자다.D는 실제 인수^∞ t의 무한히 다른 실제 함수의 공간 C에서 선형 미분 연산자가 되도록 한다.D의 고유값 방정식은 미분 방정식이다.

이 방정식을 만족시키는 함수는 D의 고유 벡터로서 흔히 고유함수라고 한다.

파생사업자의 예

고유값 방정식이 있는$$ 파생 연산자 $d{\displaystyle \frac{}{}}$ ${\displaystyle \frac{d}{}}$ d ${\$을(를) 고려하십시오.

이 미분방정식은 양쪽을 dt/f(t)로 곱하고 통합하면 해결할 수 있다.그것의 해법, 지수함수

파생사업자의 고유기능이다.이 경우 고유함수는 그 자체로 관련 고유값의 함수다.특히 λ = 0의 경우 고유함수 f(t)는 상수다.

주요 고유함수 기사는 다른 예들을 제시한다.

일반적 정의

고유값과 고유 벡터의 개념은 임의 벡터 공간의 임의 선형 변환으로 자연스럽게 확장된다.V를 스칼라의 일부 필드 K 위에 있는 벡터 공간이 되게 하고, T를 V에 매핑하는 선형 변환 공간이 되게 한다.

우리는 0이 아닌 벡터 V v V는 다음과 같은 스칼라 λ exists K가 존재하는 경우에만 T의 고유 벡터라고 말한다.

${\displaystyle T(\mathbf {v} )=\lambda \mathbf {v}.}$

(5)

이 방정식을 T에 대한 고유값 방정식이라고 하며, 스칼라 λ은 고유벡터 v에 해당하는 T의 고유값이다. T(v)는 변환 T를 벡터 v에 적용한 결과인 반면, λv는 v와 함께 스칼라 λ의 산물이다.^[36][37]

아이겐스페이스, 기하학적 다중성, 아이겐바시스

고유값 λ이 주어진 경우 세트를 고려하십시오.

즉, λ과 연관된 모든 고유 벡터의 집합과 제로 벡터의 결합이다. E는 λ과 연관된 T의 Eigenspace 또는 특성 공간이라고 불린다.

선형 변환의 정의에 의해

x, y ∈ V 및 α ∈ K의 경우.따라서 u와 v가 고유값 λ과 연관된 T의 고유 벡터, 즉 u, v ∈ E인 경우

따라서 u + v와 αv 둘 다 with과 연관된 T의 0 또는 고유 벡터, 즉 u + v, αv e E, E는 덧셈과 스칼라 곱셈에 따라 닫힌다.따라서 λ과 연관된 eigenspace E는 V의 선형 하위 공간이다.^[38]만약 그 아공간이 차원 1을 가지고 있다면, 그것은 때때로 고유선이라고 불린다.^[39]

고유값 λ의 기하학적 다중성 γ_T(λ)은 λ과 연관된 아이겐스페이스의 치수, 즉 그 아이겐값과 연관된 선형 독립형 아이겐벡터의 최대 수입니다.^[9][26]고유값과 고유벡터의 정의에 따르면 모든 고유값에는 적어도 하나의 고유벡터가 있기 때문에 γ_T(λ) ≥ 1이다.

T의 어겐스페이스는 항상 직접적인 합을 형성한다.따라서 서로 다른 고유값을 갖는 고유 벡터는 항상 선형적으로 독립적이다.따라서 아이겐스페이스 치수의 합은 T가 동작하는 벡터 공간의 치수 n을 초과할 수 없으며, n 구별되는 고유값을 초과할 수 없다.^[e]

T의 고유 벡터에 의해 확장되는 모든 하위 공간은 T의 불변 하위 공간이며, 그러한 하위 공간에 대한 T의 제한은 대각선으로 가능하다.더욱이 전체 벡터 공간 V가 T의 고유 벡터에 의해 확장될 수 있거나, T의 모든 고유값과 연관된 아이겐스페이스의 직접 합이 전체 벡터 공간 V인 경우, 아이겐바시스라고 불리는 V의 기초는 T의 선형 독립적 아이겐벡터로부터 형성될 수 있다.T가 고유근(eigenbasis)을 인정할 때, T는 대각선이 가능하다.

스펙트럼 이론

λ이 T의 고유값이라면 연산자(T - λI)는 일대일이 아니므로 역(T - λI)⁻¹은 존재하지 않는다.역은 유한차원 벡터 공간에 대해서는 사실이지만 무한 차원 벡터 공간에는 해당되지 않는다.일반적으로 연산자(T - λI)는 λ이 고유값이 아니어도 역값이 없을 수 있다.

이러한 이유로, 기능 분석에서 고유값은 연산자(T - iI)가 경계 역이 없는 모든 스칼라 λ의 집합으로서 선형 연산자 T의 스펙트럼으로 일반화할 수 있다.운영자의 스펙트럼은 항상 모든 고유값을 포함하지만 그것들에 국한되지는 않는다.

연관성 알헤브라와 표현 이론

벡터 공간에 작용하는 하나의 연산자를 대수적 표현으로 대체하여 벡터 공간에 작용하는 대수적 객체를 일반화할 수 있다. 즉, 모듈에 작용하는 연관 대수학이다.그러한 행동에 대한 연구는 대표 이론의 분야다.

무게의 표현-이론적 개념은 고유값의 아날로그인 반면, 무게 벡터와 무게 공간은 각각 고유 벡터와 고유 영역의 아날로그인 것이다.

동적 방정식

가장 간단한 차이 방정식은 형태를 가지고 있다.

${\displaystyle x_{t}=a_{1}x_{t-1}+a_{2}x_{t-2}+\cdots +a_{k}x_{t-k}.}$

t의 관점에서 x에 대한 이 방정식의 해법은 x의 특성 방정식을 사용하여 찾을 수 있다.

${\displaystyle \cdda ^{k}-a_{1}\{1}\cdda ^{k-1}-\cdots -a_{k-1}\cddda -a_{k}=0,}$

which can be found by stacking into matrix form a set of equations consisting of the above difference equation and the k – 1 equations ${\displaystyle x_{t-1}=x_{t-1},\ \dots ,\ x_{t-k+1}=x_{t-k+1},}$ giving a k-dimensional system of the first order in the stacked variable 벡터[ x x - k+ ${\$t}\$cdots &x_{$t-k+1}\$end{bmatrix}}}}}}}$이(가) 한 번 제곱된 값 측면에서 이 시스템 매트릭스의 특성 방정식을 취한다.이 방정식은 k 특성근 $\lambda {\displaystyle {}_{}}$ ${\displaystyle 1_{}}$,${\displaystyle }$… , ${\displaystyle {}_{}}$ ${\displaystyle k{}_{}}$, {\$displaystyle \lambda _{1},\ldots ,\,\lambda _${k$}$을 솔루션 방정식에 사용할 수 있도록$$ 한다.

${\displaystyle x_{t}=c_{1}\{1}\cdda _{t}+\c_{k}\c_{k}\cdots _{k}\putda _{k}^{k}^{t}.}$

유사한 절차가 형태의 미분방정식을 해결하기 위해 사용된다.

${\dfrac식 {d^{k^}x}{dt^{k-1}{dt^{k-1}{\frac {d^{k-1}{d^{k-1}}{d-1}+cdots +a_{dx}{dx}+a_{0}x=0.}$

계산

고유값과 고유벡터의 계산은 기초 선형대수학 교과서에서 제시된 이론이 종종 실제와 매우 거리가 먼 주제다.

고전적 방법

고전적 방법은 먼저 고유값을 찾은 다음 각 고유값에 대한 고유 벡터를 계산하는 것이다.그것은 부동 소수점 같은 비정확한 산술에 몇 가지 면에서 적합하지 않다.

아이겐값

행렬 $A{\displaystyle }$ ${\displaystyle A}$의 고유값은 특성 다항식의 뿌리를 찾아 결정할 수 있다$$.$이것$은 2 ${\displaystyle \times }$ $[\displaystyle 2\time 2]$ 행렬의$$ 경우 쉽지만, 난이도는 행렬의 크기에 따라 급격히 증가한다.

이론적으로, 특성 다항식의 계수는 매트릭스 원소의 생산물의 합이기 때문에 정확하게 계산할 수 있으며, 임의의 정도의 다항식의 모든 뿌리를 필요한 정확도로 찾아낼 수 있는 알고리즘이 있다.^[40]그러나 계수는 피할 수 없는 반올림 오류에 의해 오염될 수 있고 다항식의 뿌리는 계수의 극도로 민감한 함수일 수 있기 때문에(윌킨슨의 다항식 예시처럼) 이 접근법은 실제로 실행될 수 없다.^[40]요소가 정수인 행렬의 경우에도 계산이 비교가 되지 않는다. 합계가 매우 길기 때문이다. 상수 항은 $결정{\displaystyle }$ 요인이며, $n{\displaystyle }$${\displaystyle }$${\displaystyle \times }$ n ${\displaystyle n\times$ n$}$은 n! ${\displaystyn!}개$의 다른 제품의$$ 합이다.^[f]

다항식의 루트에 대한 명시적 대수 공식은 도 $n{\displaystyle }$ ${\displaystyle n}$이(가) 4 이하인 경우에만 존재한다.아벨-루피니 정리에는 5도 이상의 다항식의 뿌리에 대한 일반적이고 명시적이며 정확한 대수 공식은 없다.(도 $n{\displaystyle }$ ${\displaystyle n}$을(를) 갖는 다항식은 n ${\displaystyle$ n$}$의 일부 $동반{\displaystyle }$ 행렬의 특성 다항식이기 때문에 일반성이 중요하다.)$$따라서 순서 5 이상의 행렬의 경우 고유값과 고유 벡터는 명시적 대수 공식으로 얻을 수 없으며, 따라서 대략적인 숫자 방법으로 계산해야 한다.심지어 3도 다항식의 뿌리에 대한 정확한 공식도 숫자로는 비실용적이다.

아이겐벡터

일단 고유값의 (정확한) 값이 알려지면, 알려진 계수를 갖는 선형 방정식의 시스템이 되는 고유값 방정식의 0이 아닌 용액을 찾아 해당 고유 벡터를 찾을 수 있다.예를 들어, 일단 6이 행렬의 고유값이라는 것이 알려지면

$방정식{\displaystyle }$ ${\displaystyle A}$v = ${\displaystyle 6}$ v$${\$displaystyle Av$=6v$}$을(를) 풀면 그것의 고유 벡터를 찾을 수 있다$.$

이 행렬 방정식은 두 개의 선형 방정식과 동일하다.

즉, {- + = 0 - = $displaystyle \left\{\preligned}-2x+y&=0\6x-3y&=0\ended}\right.$$}$

두 방정식은 모두 단일 ${\displaystyle \mathrm{선형}}$ 방정식 $y{\displaystyle }$= ${\displaystyle 2}$ x ${\displaystyle y=2x}$까지 감소한다$.$Therefore, any vector of the form ${\displaystyle {\begin{bmatrix}a&2a\end{bmatrix}}^{\textsf {T}}}$, for any nonzero real number ${\displaystyle a}$, is an eigenvector of ${\displaystyle A}$ with eigenvalue ${\displaystyle \lambda =6}$.

A{A\displaystyle}위에 다른 고유 값을 가진 행렬. 비슷한 계산 3x+y는 해당 값이 조금이라도 해결책)0{3x+y=0\displaystyle}, 그 내용이 형태 T{\displaystyle{\begin{bmatrix}b&[b− 3b]어떤 벡터를 보여 주=1{\displaystyle \lambda =1}λ.앰프.$-3b\end{bmatrix}^{\textsf{T$ 0이 아닌 실제 번호 $b{\displaystyle }$ ${\displaystyle b}$에 대한 $.$

단순 반복 방법

먼저 고유 벡터를 찾고 그 고유 벡터에서 각 고유값을 결정하는 역방향 접근방식은 컴퓨터가 훨씬 더 다루기 쉬운 것으로 밝혀졌다.여기서 가장 쉬운 알고리즘은 임의의 출발 벡터를 선택한 다음 그것을 매트릭스와 반복적으로 곱하는 것으로 구성된다(선택적으로 적당한 크기의 요소를 유지하기 위해 벡터를 정상화). 이것은 벡터가 고유 벡터를 향해 수렴하게 한다.변동은 대신 벡터를${\displaystyle }$(${\displaystyle A}$ - ${\displaystyle \mu {}^{}}$I${\displaystyle {}^{}}$) - ${\displaystyle 1^{}}$ ${\$ I$)^{-1}$에 곱하는 것이다$.$ 이로 인해${\displaystyle 벡터}$는$$μ C {\$displaystyle \mu \in$ \$mathb{$C}}}에 가장 가까운 고유값의 고유 벡터로 수렴된다$.$

$v{\displaystyle \mathbf{}}$ ${\$이(가) $A{\displaystyle }${\$displaystyle A$의 고유 벡터인 경우 해당 고유값을 다음과 같이 계산할 수 있다.

${\displaystyle \lambda ={\frac {\mathbf {v} ^{*}A\mathbf {v}{\mathbf {v}}}}}}$

여기서 $∗{\$은(는) $v{\displaystyle \mathbf{}}$ ${\$의 결합 전치물을 나타낸다$$$.$

현대적 방법

임의 행렬의 고유값과 고유 벡터를 계산하는 효율적이고 정확한 방법은 1961년 QR 알고리즘이 설계되기 전까지는 알려져 있지 않았다.^[40]Householder 변환을 LU 분해와 결합하면 QR 알고리즘보다 정합성이 우수한 알고리즘이 나온다.^{[citation needed]}큰 에르미타스 희소 행렬의 경우, 란초스 알고리즘은 몇 가지 다른 가능성 중에서 고유값과 고유 벡터를 계산하는 효율적인 반복 방법의 한 예다.^[40]

때로는 구현자가 더 이상 필요하지 않은 고유 벡터 정보를 즉시 폐기하기로 선택하기도 하지만, 행렬의 고유값을 계산의 부산물로 계산하는 대부분의 숫자 방법은 해당 고유 벡터 집합을 결정하기도 한다.

적용들

기하학적 변환의 고유값

다음 표는 2×2 행렬, 고유값 및 고유 벡터와 함께 평면의 몇 가지 변환 예를 보여준다.

기하학적 변환의 고유값

	스케일링	불균등 스케일링	회전	수평전단	쌍곡선회
삽화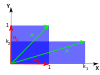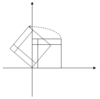
매트릭스	${\displaystyle {\bmatrix}k&0\\0&k\end{bmatrix}}$	${\displaystyle {\bmatrix}k_{1}&0\0&k_{2}\end{bmatrix}}}$	${\displaystyle {\bmatrix}\cos \theta &-\sin \theta \\sin \theta \end{bmatrix}}}}$	${\displaystyle {\bmatrix}1&k\0&1\end{bmatrix}}$	${\displaystyle {\bmatrix}\cosh \varphi &\sinh \varphi \varphi &\cosh \varphi \end{bmatrix}}}}$
특성 다항식의	${\displaystyle \(\lambda -k)^{2}}$	${\displaystyle(\displaystyle)(\displayda -k_{1})(\displayda -k_{2})$	${\displaystyle \exda ^{2}-2\cos(\theta )\cosda +1}$	${\displaystyle \(\displayda -1)^{2}}$	${\displaystyle \lambda ^{2}-2\cosh(\varphi )\barphda +1}$
고유값, $\lambda {\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$	${\displaystyle \lambda _{1}=\lambda _{2}=k}$	${\displaystyle {\regated}\baseda _{1}&=k_{1}\\\\basda _{2}&=k_{2}}\end}}}}}$	${\displaystyle {\i\i\theta }\\&=\cos \theta +i\sin \\\cHBE\{2}=e^{-i\theta }\&=\cos \theta -i\sined{taigned}}}}}}}}}}}}}}$	${\displaystyle \lambda _{1}=\lambda _{2}=1}$	${\displaystyle {\barphi }\justda _{1}&=e^{\varphi }\\&=\cosh \varphi \\\varphi \}{2}=e^{-\varphi \&=\cosh \varphi \liged{}}}}}}}}}}}}}}}}\varph \varfineed}}}}}}}}}}}}}$
대수학 , ${\displaystyle \mu _{i}=\mu(\lambda _{i})}$	${\displaystyle \mu _{1}=2}$	${\displaystyle {\regated}\mu _{1}&=1\\\mu _{2}&=1\end}}}$	${\displaystyle {\regated}\mu _{1}&=1\\\mu _{2}&=1\end}}}$	${\displaystyle \mu _{1}=2}$	${\displaystyle {\regated}\mu _{1}&=1\\\mu _{2}&=1\end}}}$
기하학적, ${\displaystyle \property_{i}=\properties(\da _{i}})}$	${\displaystyle \filename _{1}=2}$	${\displaystyle {\regated}\properties _{1}&=1\\\properties _{2}&=1\ended}}}$	${\displaystyle {\regated}\properties _{1}&=1\\\properties _{2}&=1\ended}}}$	${\displaystyle \filename _{1}=1}$	${\displaystyle {\regated}\properties _{1}&=1\\\properties _{2}&=1\ended}}}$
아이겐벡터	0이 아닌 모든 벡터	${\displaystyle {\mathbf {u} _{1}&={\bmatrix}1\\\0\end{bmatrix}\\mathbf {u} _{2}={bmatrix}0\1\end{bmatrix}}\end{bmatrix}}}}}}.$	${\displaystyle {\mathbf {u} _{1}&={\bmatrix}1\\-i\end{bmatrix}\\\mathbf {u} _{2}={bmatrix}\+i\end{bmatrix}}\end{bmatrix}}}}}}}}}$	${\displaystyle \mathbf {u} _{1}={\bmatrix}1\\0\end{bmatrix}}}$	${\displaystyle {\mathbf {u} _{1}&={\bmatrix}1\\\1\end{bmatrix}\\mathbf {u} _{2}&={bmatrix}\-1\end{bmatrix}\ended}}}}}}$

회전을 위한 특성 방정식은 $판별{\displaystyle }$ D${\displaystyle }$=${\displaystyle }$- ${\displaystyle 4}$(${\displaystyle 신\theta {}^{}}$) ${\displaystyle {2\mathrm{}}^{}}$ ${\$ D$=-4(\sin \theta )^{2$}},$$θ이 180°의 정수 배수가 아닐 때마다 음수인 것이다.따라서 이러한 특수한 경우를 제외하고 두 고유값은 복합적인 숫자로서, ${\displaystyle \cos }$ ${\displaystyle i}$ ± i sin ${\displaystyle \theta }$ ${\displaystyle \{}$ { { { { { ${$\$pm i$\sin \$theta$$}'$의 모든 고유 벡터는 비현실적인 입력을 가지고 있다.실제로 그러한 특별한 경우를 제외하고 회전은 평면의 모든 0이 아닌 벡터의 방향을 변경한다.

같은 면적의 직사각형까지 직사각형을 취하는 선형 변환(스퀴즈 매핑)은 역수 고유값을 갖는다.

슈뢰딩거 방정식

변환 $T{\displaystyle }$ ${\displaystyle T}$이(가) 미분 연산자로 표현되는 고유값 방정식의 예는 양자역학에서 시간 독립적인 슈뢰딩거 방정식이다.

${\displaystyle H\psi _{E}=E\psi _{E}\,}$

$여기서$해밀턴어인 H {\$displaystyle H}$은 2차 차동 연산자이며 파동함수인$$$\psi {\displaystyle {}_{}}$ ${\displaystyle E_{}}$ ${\$는 고유값 $E{\displaystyle }$ ${\displaysty$ E$}$에 해당하는 고유함수의 하나로$,$ 에너지로 해석된다.

그러나 슈뢰딩거 방정식의 바운드 상태 해법에만 관심이 있는 경우에는 사각형 통합함수의 공간 내에서$$ $within{\displaystyle {}_{}}$ ${\displaystyle E_{}}$ ${\$를 찾는다.이 공간은 스칼라 제품이 잘 정의된 힐버트 공간이기 때문에 $\psi {\displaystyle {}_{}}$ ${\displaystyle E_{}}$ ${\$와 $H{\displaystyle }$ ${\displaystyle H}$를 각각 1차원 배열(즉, 벡터)과 매트릭스로 나타낼 수 있는$$ 베이스를 도입할 수 있다.이를 통해 슈뢰딩거 방정식을 행렬 형태로 나타낼 수 있다.

브래킷 표기법은 이런 맥락에서 자주 사용된다.사각형 통합함수의 힐버트 공간에서 시스템의 상태를 나타내는 벡터는 ${\displaystyle \psi {\mathrm{}}_{}}$ ${\displaystyle E_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle \Psi _{E}\rangele }$로 표현된다$.$ 이 표기법에서 슈뢰딩거 방정식은 다음과 같다.

${\displaystyle H \PSI _{E}\rangele =E \PSI _{E}\rangele }$

여기서 ${\displaystyle \psi {\mathrm{}}_{}}$ ${\displaystyle E_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle \PSI _{E}\angle$ }은$($는) $H$의 고유 상태이며 $E$ ${\displaystyle E}$은 고유값을 나타낸다$$.${\displaystyle H}$ ${\displaystyle H}$은(는) 관측 가능한 자기 적응 연산자로, 은둔자 행렬의 무한 차원 아날로그다.매트릭스 사례에서와 같이, $위$의 방정식에서 H ${\displaystyle \psi {\mathrm{}}_{}}$ ${\displaystyle E_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle$H$\Psi \{E}\rangele$ $}$은(는) $변환{\displaystyle }$ H ${\\displaystyle H}$을(를) ${\displaystyle e{\mathrm{}}_{}}$ ${\displaystyle E_{}}$ ${\displaystyle {}_{}}$ ${\displaystystyle \Psi _{E}$에 적용하여 얻은 벡터로 이해된다$.$

파동 수송

빛, 음향파, 전자파는 정적인 무질서한 시스템을 통과할 때 무수히 흩어진다.는 필드 전송 매트릭스에선{\displaystyle \mathbf{t}에 의해}묘사될 수 있지만 다중 반복적으로 산란 파도 randomizes 시스템을 통한 궁극적으로 가간섭성 파 수송은 결정 과정 t † t{\displaystyle \mathbf{t}^{\dagg은 전송 사업자의 값 .[41][42].어}\ma$thbf {t} }$은(는) 파동이 정렬되지 않은 시스템의 고유 채널로 결합할 수 있도록 하는 장애별 입력 파동 세트를 형성한다$$. 즉, 독립적 경로 파동은 시스템을 통해 이동할 수 있다.$t{\displaystyle {\mathbf{}}^{}}$ ${\displaystyle {}^{}\mathbf{}}$ ${\$$displaystyle \tau$ $\}$의 고유값인 , ${\$$displaystyle \mathbf {t} ^{\dager }\mathbf {t}$는 각 고유 채널과 관련된 강도 투과율에 해당한다$$.τ 최대의 한가지 장황한 시스템의 전송 사업자의 놀랄 만한 속성 중 두가지 시스템이 있는 고유 값 분포)1{\displaystyle \tau_{\max}=1}과 τ분)0{\displaystyle \tau_{\min}=0}.[42]게다가, 개방한 eigenchannels의 그 놀라운 속성의 완벽한 투과율을 넘어서, 있다. 그고유 채널의 통계적으로 강력한 공간 프로필.^[43]

분자 궤도

양자역학, 특히 원자 및 분자물리학에서 하트리-내부는Fock 이론, 원자 및 분자 궤도는 Fock 연산자의 고유 벡터에 의해 정의될 수 있다.이에 상응하는 고유값은 쿠페만의 정리를 통해 이온화 전위로 해석된다.이 경우, Fock 연산자는 궤도와 그 고유값에 명시적으로 의존하고 있기 때문에 고유벡터라는 용어는 다소 일반적인 의미로 사용된다.따라서 이러한 측면에 밑줄을 긋고자 한다면 비선형 고유치 문제를 이야기한다.이러한 방정식은 대개 이 경우 자체 정합성 필드 방법으로 불리는 반복 절차에 의해 해결된다.양자화학에서는 하트리-을 대표하는 경우가 많다.비직교적 기준 집합의 포크 방정식.이 특별한 표현은 Rootha 방정식이라고 불리는 일반화된 고유치 문제다.

지질학과 빙하학

지질학에서 특히 빙하까지의 연구에서는 고유 벡터와 고유값을 클라스 직물의 성분 방향과 딥의 정보 덩어리를 3-D 공간에 6개의 숫자로 요약할 수 있는 방법으로 사용한다.현장에서 지질학자는 토양 샘플에서 수백 또는 수천 개의 쇄설물에 대한 그러한 데이터를 수집할 수 있는데, 이는 트리 플롯(Sneed and Folk) 다이어그램이나 ^[44][45]울프 넷의 스테레오넷처럼 그래픽적으로만 비교할 수 있다.^[46]

방향 텐서의 출력은 공간의 세 개의 직교(수직) 축에 있다.3개의 값 그들의 eigenvalues E1≥ E2≥ E3{\displaystyle E_{1}\geq E_{2}\geq E_{3}}에 의해;clast,의[47]v1{\displaystyle \mathbf{v}_{1}}다음은 기본 orientation/dip v1, v2와 3{\displaystyle \mathbf{v}_{1},\mathbf{v}_{2},\mathbf{v}_{3}}지시 받게 된다. v${\displaystyle 2_{}}$ ${\$}}은$$ 2차, $v{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {\mathrm{}}_{}}$ ${\$은 3차 강도.클라스 방향은 360°의 나침반 장미에서 고유 벡터의 방향으로 정의된다.딥은 고유값인 텐서의 계수로 측정되며, 이는 0°(딥 없음) ~ 90°(수직)까지 평가된다.$E{\displaystyle {}_{}}$ ${\$ ${\displaystyle {E\mathrm{}}_{}}$ 2 ${\$ $E{\displaystyle {}_{}}$ ${\$의 상대적 값은 침전물의 직물의 특성에 의해 지시된다$$.$E{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$= ${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$= ${\displaystyle {}_{}}$ ${\displaystyle {3\mathrm{}}_{}}$ ${\$이면 직물이 등방성이라고 한다. = > 3 ${\$$2$}}인 경우$E_{3$ 천은 평면이라고 한다. E > > E ${\$이면$E_{3$ 직물은 선형이라고 한다.^[48]

주성분 분석

대칭 양의 세미데핀(PSD) 행렬의 아이겐데 구성은 고유 벡터의 직교 기준을 산출하며, 각각은 비 음의 고유값을 갖는다.PSD 행렬의 직교 분해는 다변량 분석에서 사용되며, 여기서 표본 공분산 행렬은 PSD이다.이러한 직교 분해를 통계학에서는 주성분 분석(PCA)이라고 부른다.PCA는 변수들 사이의 선형 관계를 연구한다.PCA는 공분산 행렬 또는 상관 행렬(각 변수의 표본 분산이 1과 같도록 크기가 조정되는 경우)에서 수행된다.공분산 또는 상관 행렬의 경우 고유 벡터는 주성분에 해당하며, 고유값은 주성분에 의해 설명되는 분산에 해당한다.상관 행렬의 주성분 분석은 관측된 데이터의 공간에 대한 직교 기준을 제공한다.이 기준에서 가장 큰 고유값은 다수의 관측된 데이터 중 대부분의 공변량과 관련된 주요 성분에 해당한다.

주성분 분석은 생물정보학에서 접하는 것과 같은 대규모 데이터 집합 연구의 차원성 감소 수단으로 사용된다.Q 방법론에서 상관 행렬의 고유값은 실제 유의성에 대한 Q-방법론자의 판단(가설 검사의 통계적 유의성, 인자 수를 결정하기 위한 cf. 기준)을 결정한다.보다 일반적으로, 주성분 분석은 구조 방정식 모델링에서 인자 분석 방법으로 사용될 수 있다.

진동해석

고유치 문제는 자유도가 많은 기계적 구조물의 진동해석에서 자연적으로 발생한다.고유값은 진동의 고유진동수(또는 고유진동수)이며, 고유벡터는 이러한 진동모드의 형상이다.특히, 미장착 진동은 다음에 의해 제어된다.

또는

즉, 가속은 위치에 비례한다(즉, $우리$는 x$${\$displaystyle x$}이(가) 시간 내에 사인파일 것으로$$ 예상한다).

$n{\displaystyle }$ ${\displaystyle n}$ 치수에서$$ $m{\displaystyle }$ ${\displaystyle m}$은(는) 질량 행렬이 되고$$ $k{\displaystyle }$ ${\displaystyle k}$은 강성 행렬이 된다.허용 솔루션은 일반화된 고유값 문제에 대한 해결책의 선형 결합이다.

여기서 $\Omega {\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$은 고유값이고 $\Omega {\displaystyle }$ ${\displaystyle \omega }$은(는) 각도 주파수다.주 진동 모드는 $k{\displaystyle }$ ${\displaystyle k}$의 고유 벡터인 주 준수 모드와는 다르다.게다가, 감쇠된 진동은, 에 의해 제어된다.

소위 2차 고유값 문제로 이어지게 된다.

이는 더 큰 시스템을 해결하는 데 드는 비용으로 대수적 조작에 의해 일반화된 고유값 문제로 축소될 수 있다.

고유 벡터의 직교성 특성은 시스템이 고유 벡터의 선형 합산으로 표현될 수 있도록 미분 방정식을 디커플링할 수 있다.복잡한 구조물의 고유치 문제는 유한요소해석을 통해 해결되는 경우가 많지만, 스칼라 값이 매겨진 진동 문제에 대한 해결책을 깔끔하게 일반화한다.

아이겐파케스

이미지 처리에서 얼굴의 처리된 이미지는 각 픽셀의 밝기가 구성 요소인 벡터로 볼 수 있다.^[49]이 벡터 공간의 치수는 픽셀 수입니다.얼굴의 많은 정규화된 그림 집합과 연관된 공분산 행렬의 고유 벡터를 고유 영역이라고 한다. 이는 주성분 분석의 예다.그것들은 어떤 얼굴 이미지를 그들 중 몇몇의 선형 결합으로 표현하는데 매우 유용하다.생체 인식의 안면 인식 분기에서 고유화면은 식별을 위해 면에 데이터 압축을 적용하는 수단을 제공한다.손 제스처를 결정하는 고유 비전 시스템과 관련된 연구도 이루어졌다.

이 개념과 유사하게, 고유 음성은 언어의 단어와 같은 특정한 발음의 인간 발음의 일반적인 변동의 방향을 나타낸다.그러한 고유음의 선형 결합에 기초하여 단어의 새로운 음성 발음을 구성할 수 있다.이러한 개념들은 스피커 적응을 위한 자동 음성 인식 시스템에서 유용하게 발견되었다.

관성 모멘트 텐서

역학에서 관성 텐서 모멘트의 고유 벡터는 강체 신체의 주요 축을 정의한다.관성 모멘트의 텐서(tensor of moment of this moment)는 질량 중심 주위의 강체 몸의 회전을 결정하는 데 필요한 핵심량이다.

스트레스 텐서

고체 역학에서 응력 텐서는 대칭이므로 대각선 및 고유 벡터의 고유값을 기초로 대각선 텐서로 분해될 수 있다.대각선이기 때문에 이 방향에서 응력 텐서는 전단 구성요소가 없다. 이 텐서가 가진 구성요소는 주요 구성요소들이다.

그래프

In spectral graph theory, an eigenvalue of a graph is defined as an eigenvalue of the graph's adjacency matrix ${\displaystyle A}$, or (increasingly) of the graph's Laplacian matrix due to its discrete Laplace operator, which is either ${\displaystyle D-A}$ (sometimes called the combinatorial Laplacian) or ${\displaystyle I-D^{-1/2}}$${\$$2$$AD^{-1/2}}$ (sometimes called the normalized Laplacian), where ${\displaystyle D}$ is a diagonal matrix with ${\displaystyle D_{ii}}$ equal to the degree of vertex ${\displaystyle v_{i}}$, and in ${\displaystyle D^{-1/2}}$, the ${\displaystyle i}$th diagonal entry is $1/\sqrt{d}$$\sqrt{예}$: $\sqrt{}$($\sqrt{{}_{}}$ $){\$ 1$/{\sqrt{\deg(v_{i$ 그래프의 $주요{\displaystyle }$ 고유 벡터(k ${\$$displaystyle k$$})$는 라플라시안(Laplacian)의 최소 $고유값$인 $k{\displaystyle }$ ${\displaystyle k}$에 해당하는 고유 벡터로 정의된다.그래프의 첫 번째 주 고유 벡터는 주 고유 벡터라고도 한다.

주 고유 벡터는 정점의 중심성을 측정하는 데 사용된다.구글의 페이지랭크 알고리즘이 그 예다.월드 와이드 웹 그래프의 수정된 인접 행렬의 주요 고유 벡터는 페이지의 구성요소로 순위를 제공한다.이 벡터는 행 정규화된 인접 행렬로 대표되는 마르코프 체인의 고정 분포에 해당하지만, 인접 행렬은 고정 분포가 존재하도록 먼저 수정해야 한다.두 번째로 작은 고유 벡터는 스펙트럼 클러스터링을 통해 그래프를 클러스터로 분할하는 데 사용될 수 있다.다른 방법들도 클러스터링에 사용할 수 있다.

기본 재생산 번호

기본 생식 번호(${\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$는 전염병이 어떻게 퍼지는가에 대한 연구의 기초적인 숫자다.감염자 1명을 완전히 취약한 인구에 투입하면 $R{\displaystyle {}_{}}$ ${\$은 대표적인$$ 감염자 1명이 감염되는 평균 감염자 수입니다.감염 발생 시간은 한 사람이 감염되어 다음 사람이 감염되는 시간인 ${\displaystyle t_{}}$ $G{\displaystyle {}_{}}$ ${\$이다$.$이질적인 모집단에서 다음 세대 매트릭스는 ${\displaystyle {시간}_{}}$ t G ${\$이 경과한$$ 후 모집단에서 얼마나 많은 사람이 감염될 것인지를 규정한다.${\displaystyle R_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$은(는) 다음 세대 행렬의 최대 고유값이다.^[50][51]

참고 항목

• 항이유전가치론
• 아이겐오퍼레이터
• 아이겐플레인
• 고유값 알고리즘
• 고유스테이트 소개
• 요르단 정상 형태
• 수치분석 소프트웨어 목록
• 비선형 고유문제
• 정규 고유값
• 2차 고유값 문제
• 단수값
• 행렬의 스펙트럼

메모들

인용구

원천

추가 읽기

외부 링크

이 기사의 외부 링크 사용은 위키피디아의 정책이나 지침을 따르지 않을 수 있다. 너무 많거나 부적절한 외부 링크를 제거하고 적절한 경우 유용한 링크를 각주 참조로 변환하여 이 문서를 개선하십시오.(2019년 12월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기)

위키북 선형대수학(Wikibook Linear Galge)에는 다음과 같은 주제의 페이지가 있다: 아이겐값과 아이겐벡터

• 고유값이란 무엇인가?– PhysLink.com의 "전문가에게 물어보십시오"의 비기술적 소개
• 고유값 및 고유 벡터 수치 예제 – Rivoledu의 자습서 및 인터렉티브 프로그램.
• Eigen 벡터와 Eigen Values 소개 – Khan Academy 강연
• 고유 벡터와 고유값 선형대수의 정수, 10장 – 3Blue1Brown으로 시각적 설명
• 기호ab의 Matrix Eigen벡터 계산기(매트릭스 크기를 선택하려면 2x12 그리드의 오른쪽 하단 버튼을 클릭하십시오.(제곱 행렬의 경우) $n{\displaystyle }$ ${\displaystyle \times }$ ${\displaystyle n}$ ${\displaystyle n\times n}$ 크기를$$ 선택한 다음 숫자를 입력하고 이동 버튼을 클릭하십시오.복잡한 숫자도 받아들일 수 있다.)

이론

• 고유값 계산
• 고유치 문제의 수치적 해결책 자오준 바이, 제임스 뎀멜, 잭 동가라, 액셀 루헤, 헨크 판 데어 보르스트 편집