바이알게브라

이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "Bialgebra" – 뉴스 · 신문 · 책 · 학자 · JSTOR(2009년 12월) (이 템플릿 메시지를 제거하는 방법과 시기 학습)

수학에서 K영역 위에 있는 이알지브라(bialgebra)는 K영역 위에 있는 벡터공간으로, 이 둘 다 단일 연관대수학이고 카운티 공동연관합동합동대수학에서 K영역 위의 이알지브라(belgebra)는 K영역 위에 있는 벡터공간이다.대수학적 구조와 결합형 구조는 몇 가지 더 많은 공리와 양립할 수 있도록 만들어졌다.구체적으로는 배합과 상담은 모두 단수대수동형, 또는 동등하게 대수의 곱과 단위는 모두 합수대수형이다.(이러한 진술은 같은 역수형 도표로 표현되기 때문에 등가한다.)

유사한 바이알게브라는 바이알게브라의 동음이의식과 관련이 있다.바이알게브라 동형성(bialgebra homorphism)은 대수학(大學)이면서 동시에 합게브라 동형성(collgebra homorphism)인 선형 지도다.

정류 도표의 대칭에 반영되듯이 바이알지브라 정의는 자가이중이므로 B의 이중(B가 유한한 차원일 경우 항상 가능한 것)을 정의할 수 있다면 자동으로 바이알지브라(bialgebra)가 된다.

대수구조
그룹다운 그룹 세미그룹 / 모노이드 랙 앤 퀀들 Quas그룹과 루프 아벨 군 마그마 거짓말군 집단 이론
반지 같은 울리다 Rng 세미닝 근링 정류 링 통합 도메인 밭 디비전 링 리 링 링 이론
격자 모양의 격자 세미라티체 보완 격자 총순번 헤이팅 대수 부울 대수 선반 지도 격자 이론
모듈형 모듈 연산자와 그룹화 벡터 공간 선형대수학
대수적 유사 대수학 연상적 비연관적 구성 대수 리 대수 등급이 매겨진 바이알게브라 호프 대수
v t

형식 정의

(B, ∇, η, Δ, ε)는 K 위에 있는 바이알지브라(bialgebra)로서, 다음과 같은 성질을 가지고 있는 경우, K 위에 있는 바이알지브라(balgebra)이다.

• B는 K 위의 벡터 공간이다.
• K-선형 지도(증법) ∇: B ⊗ B → B (K-멀티라인 지도 ∇: B × B → B) 및 (단위) →: K → B (B, ∇, η)가 있는데, 이는 (B, ∇, η)가 단역적 연관 대수학이다.
• K-선형 지도(복제) Δ: B → B ⊗ B 및 (복제) :: B → K가 있는데, (B, Δ, ε)는 (복제적 공동 연관) 결합형이다.
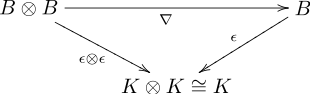
• 다음 정류 도표로 표현되는 호환성 조건:

1. 곱셈 ∇과 곱셈 Δ^[1]

   

   여기서 τ: B ⊗ B → B ⊗ B는 B의 모든 x와 y에 대해 y(x ⊗ y) = y ⊗ x로 정의된 선형 지도다.

2. 곱하기 ∇ 및 상담 ε

   

3. 콤멀티제이션 Δ 및 단위 η^[2]

   

4. 단위 η 및 상담 ε

   

협동조합과 상담

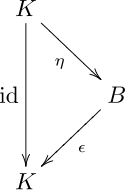
The K-linear map Δ: B → B ⊗ B is coassociative if ${\displaystyle (\mathrm {id} _{B}\otimes \Delta )\circ \Delta =(\Delta \otimes \mathrm {id} _{B})\circ \Delta }$.

The K-linear map ε: B → K is a counit if ${\displaystyle (\mathrm {id} _{B}\otimes \epsilon )\circ \Delta =\mathrm {id} _{B}=(\epsilon \otimes \mathrm {id} _{B})\circ \Delta }$.

공동 연관성과 상담은 다음 두 도표의 공통성으로 표현된다(그 도표는 연관성과 대수적 단위를 표현하는 도표의 이중성이다).

호환성 조건

네 개의 대응 도표는 "복제 및 상담은 알헤브라의 동형상" 또는 동등하게 "복제 및 단위는 콜게브라의 동형상"으로 읽을 수 있다.

이러한 진술들은 일단 우리가 B를 제외하고 관련된 모든 벡터 공간에서 대수학 및 결합형의 자연구조를 설명하면 의미가 있다: (K, ∇,₀ η₀)는 단위의 결합 대수학이고 (B ⊗ B, ∇,₂ η₂, unit)는 단위와 곱셈이 있는 단위의 결합 대수학이다.

${\displaystyle \eta _{2}:=(\eta \otimumes \eta ):K\oth K\equiv K\to (B\oth B)}$

$∇$$(B\oth$ B$)\to(B\oth$ B$)\},$

so that ${\displaystyle \nabla _{2}((x_{1}\otimes x_{2})\otimes (y_{1}\otimes y_{2}))=\nabla (x_{1}\otimes y_{1})\otimes \nabla (x_{2}\otimes y_{2})}$ or, omitting ∇ and writing multiplication as juxtaposition, ${\displaystyle (x_1\otimes x_2}$${\displaystyle )({}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$)${\displaystyle }$= x ${\displaystyle {}_{}}$ ${\displaystyle {y\mathrm{}}_{}}$ 1 ${\displaystyle {}_{}}$ x ${\displaystyle {}_{}}$ ${\displaystyle {}_{}{}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$2}} ; $;;$

이와 유사하게 (K₀, Δ₀, ))는 명백한 방법으로 합금이고, B ⊗ B는 협의와 복제가 있는 합금이다.

${\displaystyle \epsilon _{2}=(\epsilon \otimes \epsilon }):(B\otimes B)\to K\otimes K\equiv K}$

${\displaystyle \Delta _{2}:=(id\otimes \tau \otimes id)\circ (\Delta \otimes \Delta ):(B\otimes B)\to (B\otimes B)\otimes (B\otimes B)}$.

그렇다면 도표 1과 3에 의하면 Δ: B → B ⊗ B는 단이탈(연관) 알헤브라스(B, ∇, η₂)와 (B ⊗ B,₂ ,, ))의 동형상이다.

${\displaystyle \Delta \circ \nabla =\nabla _{2}\circ (\Delta \otimes \Delta ):(B\otimes B)\to (B\otimes B)}$, or simply Δ(xy) = Δ(x) Δ(y),

$displaystyle$$$$K\to(B\otimes B)}$또는 단순 Δ(1_B) = 1_{B ⊗ B};

도표 2와 4는 ε: B → K는 단핵(연관) 알헤브라스(B, ∇, η)와 (K, ∇,₀ η₀)의 동형상이다.

${\displaystyle \epsilon \circ \nabla =\nabla _{0}\circ (\epsilon \otimes \epsilon ):(B\otimes B)\to K}$, or simply ε(xy) = ε(x) ε(y)

${\displaystyle \엡실론 \circle \eta$$K\to K$ 또는 간단히 ε_B(1) = 1_K.

동등하게 도표 1과 2는 ∇: B ⊗ B → B는 (상호조합) 합골(B ⊗ B, Δ₂, ε₂)과 (B, Δ, ε)의 동형상이라고 한다.

$\displaystyle \nabla \otimes \nabla \circla \Delta _{2}=\delta \circla :(B\otimes B)\to(B\otimes B),}$

${\displaystyle {\mathrm{\nabla }}_{}}$ ${\displaystyle {0\mathrm{}}_{}{}_{}}$∘ ${\displaystyle {}_{}}$ ${\displaystyle 2}$ = ${\displaystyle \circ }$ ∇${\displaystyle \mathrm{\nabla }}$ : ${\displaystyle (B)}$ ${\displaystyle B}$ )${\displaystyle }$→ K ${\displaystyle \nabla _{0$}\circlon$\epsilon \c \circ \nabla$ : ($B\$otimes B)\$to$ K$}$ $;;;$

도표 3과 4에 의하면 :: K → B는 (상호조합) collgebras (K, Δ₀, ε₀)와 (B, Δ, ε)의 동형상이다.

${\displaystyle \eta _{2}\circle \Delta _{0}=\Delta \circle \eta :K\to (B\oth B),}$

${\displaystyle {\eta }_{}}$ ${\displaystyle {0\mathrm{}}_{}{}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$= ${\displaystyle ϵ}$ ${\displaystyle \circ \eta }$ : ${\displaystyle K}$→ K ${\displaystyle \eta \{0}\circlon \epsilon _{0}=\epsilon \circlon \eta :K\to K$ ,

어디에

${\displaystyle {ϵ}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$= ${\displaystyle ϵ\eta }$ η ${\displaystyle \epsilon _{0}=\epsilon \eta$ $\}.$

예

그룹 바이알지브라

기능은 그룹 G(또는 더 일반적으로 말해서, 어떤monoid)에서 R{\displaystyle \mathbb{R}으로 벡터 공간으로 나타낼 수도 있는 bialgebra의 예는 세트}, RG(^{G}}의 선형 조합의 표준 기준 벡터 eg의 각 g∈ G, 있는을 나타낼 가능성이 경멸하다.t계수가 모두 음수가 아니고 합이 1인 벡터의 경우 G에 대한 늑골.적절한 복제 운영자 및 상담의 예로서, 카운티 통합지점을 산출한다.

${\displaystyle \Delta (\mathbf {e} _{g}=\mathbf {e} _{g}\otimes \mathbf {e} _{g}\}}$

즉, 임의 변수의 복사본을 만드는 것을 의미한다(모든$$ $R{\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {}^{}}$ ${\$

${\displaystyle \varepsilon(\mathbf {e} _{g}=1\...}$

(또한 R $G{\displaystyle {\mathbb{}}^{}}$ ${\$ 모든 R ${\displaystyle {}^{}}$ {\displaystyle \mathb {R} ^{G$\}\})$로 선형 확장되었으며, 이는 랜덤 변수 값(단일 텐서 계수로 표현됨)을 잊어버리고 나머지 변수(남은 텐서 요인)에 대한 한계 분포를 구한다.위와 같이 확률분포 측면에서 (Δ,³)의 해석을 고려할 때, 바이알지브라 일관성 조건은 다음과 같이 (∇, η)에 대한 제약조건에 해당한다.

1. η은 다른 모든 랜덤 변수와 독립된 정규화된 확률 분포를 준비하는 연산자다.
2. 제품 ∇은 두 변수의 확률 분포를 하나의 변수의 확률 분포에 매핑한다.
3. η이 제공한 분포에서 랜덤 변수를 복사하는 것은 분포 η에 두 개의 독립 랜덤 변수가 있는 것과 동일하다.
4. 두 랜덤 변수의 곱을 취해서 그 결과 랜덤 변수의 복사본을 준비하는 것은 각 랜덤 변수의 복사본을 서로 독립적으로 준비하여 쌍으로 곱하는 것과 동일한 분포를 갖는다.

이러한 제약을 충족하는 쌍(쌍, ∇)은 콘볼루션 연산자다.

${\displaystyle \bigla {\bigl (}\mathbf {e} _{g}\otimes \mathbf {e} _{h}{\bigr )}=\mathbf {e} _{gh}\mathbf {e}$

again extended to all ${\displaystyle \mathbb {R} ^{G}\otimes \mathbb {R} ^{G}}$ by linearity; this produces a normalized probability distribution from a distribution on two random variables, and has as a unit the delta-distribution ${\displaystyle \eta =\mathbf {e} _{i}\;,}$ where i ∈ G denotes th그룹 G의 e ID 요소.

기타 예

다른 바이알게브라의 예로는 텐서 대수학을 들 수 있는데, 이것은 적절한 콤뮬레이션과 상담을 추가함으로써 바이알게브라로 만들 수 있다; 이것들은 그 글에서 자세히 설명된다.

바이알게브라는 적절한 대척점을 찾을 수 있다면 종종 홉프 알제브라스까지 확장될 수 있다.그러므로 모든 홉프 알제브라는 바이알게브라의 예다.^[3]제품과 복제가 서로 호환성이 다른 유사한 구조 또는 다른 유형의 곱셈과 복제가 있는 유사한 구조로는 Lie Bialgebras와 Probenius Algebrey bialgebras and Frobenius algebras가 있다.콜브라에 관한 기사에는 추가적인 예가 제시되어 있다.

참고 항목

• 준바이알지브라

메모들

참조

• Dăscălescu, Sorin; Năstăsescu, Constantin; Raianu, Șerban (2001), Hopf Algebras: An introduction, Pure and Applied Mathematics, vol. 235 (1st ed.), Marcel Dekker, ISBN 0-8247-0481-9.