육각형
Hexagon| 정육각형 | |
|---|---|
 정육각형 | |
| 유형 | 정규 다각형 |
| 모서리 및 정점 | 6 |
| 슐레플리 기호 | {6}, t{3} |
| 콕시터-딘킨 도표 | |
| 대칭군 | 디헤드랄(D6), 2×6 주문 |
| 내부 각도(도) | 120° |
| 특성. | 볼록, 주기, 등변, 이등변, 동위원소 |
기하학에서 육각형(그리스어 ἕξ, 헥스, "6"을 의미하며, "코너, 각도"를 의미하는 γΩ gonα, 고니아)은 6면 다각형 또는 6곤이다.단순(자체 교차되지 않는) 육각의 내부 각도는 720°이다.
정육각형
일반 육각형에는 슐래플리 기호 {6}[1]이(가) 있으며, 잘린 등변 삼각형, t{3}(으)로 구성될 수도 있으며, 이 경우 두 가지 유형의 가장자리가 번갈아 나타난다.
정육각형은 정육각형과 등각형의 육각형으로 정의된다.2원형이며, 둘 다 순환(원형)과 접선(원형이 새겨져 있음)이라는 뜻이다.
옆면의 공통 길이는 원 또는 원형의 반지름과 같으며, 이는 아포템(기각 원의 반지름)의 2 {과 같다.모든 내부 각도는 120도 입니다.일반 육각형에는 6개의 회전 대칭(순서 6의 회전 대칭)과 6개의 반사 대칭(대칭 6줄)이 있어 이음계 그룹 D를6 이룬다.정점과 정반대방향으로 연결되는 일반 육각형의 가장 긴 대각선은 한 변의 두 배 길이다.이를 통해 정점을 가진 삼각형이 정육각형의 중심에 있고 한쪽을 육각형과 공유하는 것을 알 수 있으며, 정육각형은 정삼각형 6개로 나눌 수 있다.
정삼각형이나 정삼각형처럼 일정한 육각형이 틈새 없이 서로 맞아 평면 타일(각 꼭지점에서 만나는 세 개의 육각형)을 만들어 테셀레이션(테셀레이션)벌집 벌집의 세포는 이러한 이유로 육각형이며, 그 모양이 공간과 건축자재를 효율적으로 사용하기 때문이다.정삼각형 격자의 보로노이 도표는 육각형의 벌집 테셀레이션이다.그것은 정삼각형이지만 보통 삼삼각형으로 여겨지지 않는다.
매개변수
최대 직경(육각형의 긴 대각선에 해당함), D는 최대 반지름의 두 배 또는 측면 길이 t와 동일한 원곡선, R이다.새겨진 원의 최소 직경 또는 직경(평행면, 평면 대 평탄한 거리, 평탄한 베이스에 쉴 때 짧은 대각선 또는 높이의 분리), d는 최소 반지름의 두 배 또는 인라디우스, r이다.maxima와 minima는 동일한 요인에 의해 연관된다.
- and, similarly,
정규 육각형 영역
어떤 일반 다각형의 경우, 면적은 또한 아포템 a와 둘레 p의 용어로 표현될 수 있다.일반 육각형의 경우 a = r, p= R= 따라서
정규 육각형은 원형의 3 0 약을(를) 채운다.
일반 육각형에는 연속 정점 A, B, C, D, E, F가 있고, P가 B와 C 사이의 원주에 있는 어떤 점이라면 PE + PF = PA + PB + PC + PD가 된다.
일반 육각형의 높이 대 너비 비율이 1:1.1547005 즉, 대각선 길이가 1.0000000인 육각형의 평행면 간 거리는 0.8660254이다.
평면 내 점
일반 육각형의 중심과 까지의거리가 각각L {\ 과d i {\ d_인 일반 육각형 {\이(가) 있는 평면의 임의 점에 대해, 우리는[2] 다음과 같이 한다.
이(가) 일반 육각의 꼭지점에서 원주형의 어떤 지점까지의 거리라면,
대칭
| 대칭에 따른 16진수 예제 | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|

정육각형은 D 대칭이다6.16개의 부분군이 있다.8가지까지 이형성(이형성)이 있다: 그 자체(D6), 2개의 이형성:(D3,2 D), 4개의 순환: (Z63, Z, Z1, Z2)와 사소한 (e)
이 대칭들은 정규 육각형의 9개의 뚜렷한 대칭을 표현한다.존 콘웨이는 문자와 그룹 순서로 이것들을 표시한다.[3] r12는 완전한 대칭이며, a1은 대칭이 아니다. p6, 세 개의 거울에 의해 구성된 이등각 육각형은 긴 가장자리와 짧은 가장자리와 d6는 가장자리 길이가 같지만 정점이 두 개의 서로 다른 내부 각도를 교차하는 동위원소 육각이다.이 두 형태는 서로 이중으로 되어 있으며, 정육각형의 대칭 순서의 절반을 가지고 있다.i4 형태는 하나의 대칭 방향을 따라 평평하게 펴지거나 늘어난 정규 육각형이다.길쭉한 광맥으로 볼 수 있는 반면 d2와 p2는 수평과 수직으로 길쭉한 연으로 볼 수 있다.g2 6각형, 반대쪽이 평행한 것을 육각형 평행고곤이라고도 한다.
각 부분군 대칭은 불규칙한 형태에 대해 하나 이상의 자유도를 허용한다.g6 부분군만 자유도는 없지만 지시된 가장자리로 볼 수 있다.
대칭 g2, i4, r12의 헥사곤은 평행고곤으로서 유클리드 평면을 번역하여 테셀링할 수 있다.다른 육각형 모양은 다른 방향으로 평면을 타일링할 수 있다.
| p6m(*632) | cmm(2*22) | p2(222) | p31m(3*3) | pmg(22*) | pg(××) | |
|---|---|---|---|---|---|---|
 r12년 |  i4 |  g2 |  d2 |  d2 |  p2 |  a1 |
| 디흐6 | 디흐2 | Z2 | 디흐1 | Z1 | ||
A2 및 G2 그룹
 A2 그룹 루트 |  G2 그룹 루트 |
Dynkin 도표로 대표되는 심플한 Lie 그룹 A2의 6개의 뿌리는 규칙적인 육각형 패턴으로 되어 있다.두 개의 단순한 뿌리는 서로 120°의 각도를 가지고 있다.
다인킨 도표로 대표되는 Excellence Lie 그룹 G2의 12개의 뿌리 역시 육각형 무늬로 되어 있다.두 길이의 단순한 두 뿌리 사이에는 150°의 각도가 있다.
해부
| 6각 투영법 | 12 롬브 해부 | |
|---|---|---|
 |  |  |
Coxeter은 모든 zonogon(한 2m-gon의 반대편과 같은 길이의 평행).mw-parser-output .frac{white-space:nowrap}.mw-parser-output.frac.num,.mw-parser-output.frac .den{:80%;line-height:0;vertical-align:슈퍼 font-size}.mw-parser-output.frac .den{vertical-align:서브}.mw-parser-output .sr-only{에 해부할 수 있다는 것.국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}1⁄2m(m− 1)parallelograms.[4]특히 면적이 고르게 많은 일반 다각형의 경우, 이 경우 평행사변형은 모두 rhombi이다.일반 육각형의 이러한 분해는 정사각형 6개의 면 중 3개를 가진 정육면체의 페트리 폴리곤 투영에 기초한다.큐브의 다른 병렬형 및 투영 방향은 직사각형 큐보이드 내에서 해부된다.
| 육각형을 세 개의 rhomb와 parallelogram으로 분리 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2D | Rhombs | 평행사변수 | |||||||||
 |  |  |  | ||||||||
| 일반 {6} | 육각 평행고선 | ||||||||||
| 3D | 정사각형 | 직사각형 면 | |||||||||
 |  |  |  | ||||||||
| 큐브 | 직사각형 큐빅 | ||||||||||
관련 폴리곤 및 틸팅
일반 육각형에는 슐레플리 기호 {6}이(가) 있다.정육각형은 정육각형 타일링 {6,3}의 한 부분으로, 각 정점 주위에 세 개의 육각면이 있다.
슐래플리 기호 t{3}와 함께, 일반 육각형은 잘린 등변 삼각형으로도 생성될 수 있다.두 가지 유형의 가장자리(색상)로 볼 수 있는 이 형태는3 D 대칭만 가진다.
잘린 육각형, t{6}는 도데카곤, {12}이며, 두 가지 유형의 가장자리(색)를 번갈아 사용한다.교대 육각형, h{6}는 정삼각형, {3}이다.일반 육각형은 가장자리에 등각 삼각형을 달아서 육각형을 만들 수 있다.정육각형은 중앙점을 추가하여 6개의 등변 삼각형으로 해부할 수 있다.이 패턴은 규칙적인 삼각 타일링 안에서 반복된다.
정육각형은 그 둘레에 정사각형과 정삼각형을 번갈아 넣어 정삼각형으로 확장할 수 있다.이 패턴은 림빗리헥스각형 타일링(Rhombitrihexangular tiling)
 |  |  |  | 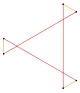 |  |  |  |
| 정규 {6} | 잘림 t{3} = {6} | 비대칭삼각형 | 스텔라티드 별 피겨2{3} | 잘림 t{6} = {12} | 교대형 h{6} = {3} | ||
|---|---|---|---|---|---|---|---|
 |  |  |  | 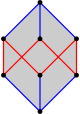 |  |  |  |
| 교차됨 육각형의 | 오목 육각형 | 자가 교차 육각형(별 폴리곤) | 확장됨 {12}의 중앙 {6} | 큐브 내의 스큐 육각형 | 해부된 {6} | 투영 팔면체 | 전체 그래프 |
|---|
자동 교차 육각형
정규 육각형의 꼭지점 배열을 가진 6개의 자교 육각형이 있다.
| 디흐2 | 디흐1 | 디흐3 | |||
|---|---|---|---|---|---|
 그림-8 |  중앙 플립 |  유니쿠르스어 |  물고기꼬리 |  이중꼬리 | 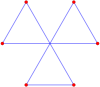 트리플테일 |
육각 구조
벌의 꿀벌부터 거인의 코즈웨이까지 육각형 무늬가 자연에 만연해 있는 것은 효율 때문이다.육각 격자에서 각 선은 가장 적은 수의 육각형으로 채워질 경우 가능한 한 짧다.이것은 허니컴이 왁스를 덜 필요로 하고 압축 하에서 많은 힘을 얻는다는 것을 의미한다.
가장자리가 평행하게 반대편인 불규칙한 육각형을 평행고곤이라고 하며, 평면을 번역하여 타일링할 수도 있다.3차원에서는 평행한 반대면이 있는 육각형 프리즘을 병렬로헤드론(Paralleloheadron)이라고 하며, 이를 번역하여 3공간을 테셀레이트할 수 있다.
| 형태 | 육각 타일링 | 육각 프리즘 벌집 |
|---|---|---|
| 정규 |  |  |
| 평행사변형 |  |  |
육각형 테셀레이션
평면의 독특한 다듬기를 결정하는 일반 육각형 외에, 콘웨이 기준을 만족하는 불규칙한 육각형은 평면에 타일을 입힌다.
원뿔 단면에 새겨진 육각형
파스칼의 정리("Hexagrammum Misticum Organy"라고도 한다)에는 임의의 육각형이 원뿔 부분에 새겨져 있고, 그들이 만날 때까지 반대편의 쌍이 확장되면, 세 개의 교차점이 그 구성의 "Pascal 선"인 직선에 놓여지게 된다고 명시되어 있다.
주기 육각형
레모인 육각형(Lemoine 6각형)은 삼각형의 가장자리의 6개 교차로에 의해 정점이 주어지는 주기적인 육각형(원형으로 새겨진 1개)이며, 시메디안 점을 통과하는 가장자리와 평행한 3개의 선이다.
주기적인 육각형의 연속적인 면이 a, b, c, d, e, f인 경우, 만약 에이스 = bdf인 경우에만 세 개의 주요 대각선이 한 점에서 교차한다.[5]
주기적인 육각형의 각 면에 대해 인접한 면이 주어진 면으로 바깥쪽으로 삼각형을 형성하면서 교차점까지 확장되는 경우, 반대 삼각형의 원곡선을 연결하는 세그먼트가 동시에 이루어진다.[6]
만약 6각형이 삼각형의 확장된 고도가 원곡선과 만나는 6점(삼각형 정점 포함)에서 급성 삼각형의 원곡선에 정점이 있다면, 6각형의 면적은 삼각형의 두 배가 된다.[7]: p. 179
원뿔 단면에 접하는 육각형
ABCDEF는 원뿔 단면의 6개의 접선 선으로 형성된 육각형이다.그 후 브리안콘의 정리에는 3개의 주요 대각선 AD, BE, CF가 한 지점에서 교차한다고 되어 있다.
원과 접하고 연속된 면 a, b, c, d, e, f를 가진 육각형에서,[8]
임의의 육각형 변에 있는 등각 삼각형
만약 정삼각형이 육각형의 양쪽에 외적으로 형성된다면, 반대 삼각형의 중심을 연결하는 세그먼트의 중간점은 다른 정삼각형을 형성한다.[9]: Thm. 1
스큐 육각형

스큐 육각형은 6개의 정점과 가장자리가 있지만 동일한 평면에 존재하지 않는 스큐 다각형이다.그러한 육각형의 내부는 일반적으로 정의되어 있지 않다.스큐 지그재그 육각형에는 두 평면이 번갈아 가며 정점이 있다.
정규 스큐 육각형은 가장자리 길이가 같은 정점 변환이다.3차원에서는 지그재그 스큐 육각형이 될 것이며, 동일한3d D, [2+,6] 대칭인 순서 12의 삼각형 항정신병증의 정점과 측면 가장자리에서 볼 수 있다.
큐브와 팔면체(삼각형 항정신병)는 쁘띠 폴리곤으로 고정된 꼬치 육각형을 가지고 있다.
 큐브 | 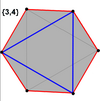 팔면체 |
페트리 폴리곤
일반 스큐 육각형은 다음과 같은 스큐 직교 투영에서 볼 수 있는 이러한 고차원 정규, 균일 및 이중 폴리헤드라 및 폴리탑에 대한 Petrie 폴리곤이다.
| 4D | 5D | |
|---|---|---|
 3-3 듀오프리즘 | 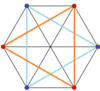 3-3 듀오피라미드 |  5와섹스 |
볼록 등각형 육각형
육각형의 주요 대각선은 육각선을 사각선으로 나누는 대각선이다.공통 면 a가 있는 볼록한 등각형 육각형(모든 면이 동일한 1개)에는 다음과 같은 주요 대각선[10]: p.184, #286.3 1 d가 있다.
그리고 주요 대각선 d는 다음과2 같다.
육각형 폴리헤드라
헥사곤 테셀레이트(tessellate)가 일반 육각체로만 만들어진 플라토닉 고체는 없으며, 그 결과가 "접혀지는" 것을 허용하지 않기 때문이다.일부 육각형의 얼굴을 가진 아르키메데스 고형물은 잘린 사면체, 잘린 팔면체, 잘린 이코사면체(축구공과 풀레렌 명성), 잘린 육면체, 잘린 이코사면체 등이다.이러한 16진법은 형식 및 의 Coxeter 다이어그램과 함께 잘린 삼각형으로 간주할 수 있다.
| 아르키메데스 고형물의 헥사곤 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 사면체 | 팔면체 | 이코사헤드랄 | |||||||||
 잘린 사면체 |  잘린 팔면체 |  잘린 칸옥타헤드론 |  잘린 이두면체 |  잘린 이코시다데카헤드론 | |||||||
이러한 골드버그 다면체 G(2,0)와 같이 확장되거나 평평해진 육각형을 가진 다른 대칭 다면체도 있다.
| 골드버그 다면체의 헥사곤 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 사면체 | 팔면체 | 이코사헤드랄 | |||||||||
 참페어드 사면체 |  챔페드 큐브 |  참페어드 도데카헤드론 | |||||||||
또한 정규 육각형을 가진 9개의 존슨 고형분들도 있다.
| 헥사곤이 있는 존슨 솔리드 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 삼각 큐폴라 |  길쭉한 삼각 큐폴라 |  길쭉한 삼각 큐폴라 | |||||||||
 증강 육각 프리즘 |  파라비증강 육각 프리즘 |  메타볼루션 육각 프리즘 |  3중증식 육각 프리즘 | ||||||||
 증강 절단 사면체 |  삼각 헤베스페노로툰다 | 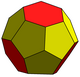 잘린 삼면체 4면체 | |||||||||
| 헥사곤 프리즘형 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 육각 프리즘 |  육각 항정신병 |  육각형 피라미드 | |||||||||
| 일반 육각형이 있는 틸링 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 정규 | 1시 30분 | ||||||||||
| {6,3} | r{6,3} | rr{6,3} | tr{6,3} | ||||||||
 |  |  |  | ||||||||
| 2-10 틸팅 | |||||||||||
 |  |  |  | ||||||||
자연 및 인공 육각형 갤러리
그래핀의 이상적인 결정 구조는 육각 격자다.
조립된 E-ELT 미러 세그먼트
벌집 벌집
거북의 등딱지 소리
토성의 육각형, 행성의 북극을 둘러싼 육각형 구름무늬
육각 방향족 링으로 구성된 분자 육각형의 결정 구조.
건조한 토르투가스 국립공원에 있는 제퍼슨 요새의 모습
메트로폴리탄 프랑스는 어렴풋이 육각형 모양을 하고 있다.프랑스어로 l'헥사곤'은 프랑스의 유럽 본토를 가리킨다.
브와디스와프 글리아스키의 육각형 체스
타이완 식물원의 정자
참고 항목
- 24세포: 육각형처럼 직교적인 면을 가진 4차원 형상으로, 자기 이중이고 유클리드 공간이다.
- 육각결정계
- 육각수
- 육각 타일링: 평면에 육각 타일링으로 구성된 정규 타일링
- 육각형: 일반 육각형 내의 육면 항성
- 유니쿠르식 육각형: 단일 경로, 6면 항성, 육각형 내
- 허니콤 추측
- 하바나: 6면 육각 격자 위에서 하는 추상 보드 게임
참조
- ^ Wenninger, Magnus J. (1974), Polyhedron Models, Cambridge University Press, p. 9, ISBN 9780521098595, archived from the original on 2016-01-02, retrieved 2015-11-06.
- ^ a b Meskhishvili, Mamuka (2020). "Cyclic Averages of Regular Polygons and Platonic Solids". Communications in Mathematics and Applications. 11: 335–355. arXiv:2010.12340.
- ^ 존 H. 콘웨이, 하이디 버기엘, 차임 굿맨-스트라우스, (2008) 사물의 대칭성, ISBN 978-1-56881-220-5 (20장, 일반화 셰플리 기호, 다각형의 대칭 유형 275-278)
- ^ Coxeter, 수학 오락 및 에세이, 13판, 페이지 141
- ^ Cartensen, Jens, "About hexagons", Matheical Spectrum 33(2)(2000–2001), 37–40.
- ^ Dergiades, Nikolaos (2014). "Dao's theorem on six circumcenters associated with a cyclic hexagon". Forum Geometricorum. 14: 243–246. Archived from the original on 2014-12-05. Retrieved 2014-11-17.
- ^ 존슨, 로저 A, 어드밴스트 유클리드 기하학, 도버 출판물, 2007년(원점)1960).
- ^ 구티에레스, 안토니오, "헥사곤, 새긴 원, 접선, 세미퍼미터", [1] 웨이백머신에 2012-05-11 보관, 2012-04-17 액세스.
- ^ Dao Thanh Oai (2015). "Equilateral triangles and Kiepert perspectors in complex numbers". Forum Geometricorum. 15: 105–114. Archived from the original on 2015-07-05. Retrieved 2015-04-12.
- ^ "Crux Mathematicorum"에서 제안된 불평등 [2] 웨이백머신에 2017-08-30 보관.
외부 링크
| 무료 사전인 Wiktionary에서 육각형을 찾아 보십시오. |
- 대화형 애니메이션과 나침반 및 직선자를 사용한 구조로 구성된 육각형의 정의 및 특성.
- 육각수학 전문 웹사이트인 육각형 기하학 소개
- 헥사곤은 헥사곤에 관한 애니메이션 유튜브 동영상이다.
| 가족 | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 정규 다각형 | 삼각형 | 사각형 | p-곤 | 육각형 | 펜타곤 | |||||||
| 균일다면체 | 사면체 | 옥타헤드론 • 큐브 | 데미큐브 | 도데카헤드론 • 이코사헤드론 | ||||||||
| 균일 폴리초론 | 펜타코론 | 16-셀 • 테세락트 | 데미테세락트 | 24셀 | 120 셀 • 600 셀 | |||||||
| 제복5폴리토프 | 5와섹스 | 5정형 • 5정형 | 5데미큐브 | |||||||||
| 제복6폴리토프 | 6-630x | 6-정통 • 6-118 | 6데미큐브 | 122 • 221 | ||||||||
| 제복7폴리토프 | 7시 15분 | 7정맥 • 7정맥 | 7데미큐브 | 132 • 231 • 321 | ||||||||
| 제복8폴리토프 | 8시 15분 | 8정형 • 8정형 | 8데미큐브 | 142 • 241 • 421 | ||||||||
| 제복9폴리토프 | 9시 15분 | 9-정통 • 9-11 | 9데미큐브 | |||||||||
| 균일 10폴리토프 | 10센트짜리 | 10정형 • 10정형 | 10데미큐브 | |||||||||
| 균일 n폴리토프 | n-제곱스 | n-직관 • n-직관 | n-데미큐브 | 1k2 • 2k1 • k21 | n-자갈 폴리토프 | |||||||
| 주제: 폴리토페 패밀리 • 일반 폴리토페 • 일반 폴리토페 및 화합물 목록 | ||||||||||||



 2
2 


![{\displaystyle {\begin{aligned}A&={\frac {3{\sqrt {3}}}{2}}R^{2}=3Rr=2{\sqrt {3}}r^{2}\\[3pt]&={\frac {3{\sqrt {3}}}{8}}D^{2}={\frac {3}{4}}Dd={\frac {\sqrt {3}}{2}}d^{2}\\[3pt]&\approx 2.598R^{2}\approx 3.464r^{2}\\&\approx 0.6495D^{2}\approx 0.866d^{2}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67e6b4ae01ba9dc79d7c7dd7fa50b2613799966c)














































