딘킨 도표
Dynkin diagram| 거짓말 그룹 |
|---|
 |
Lie 이론의 수학 분야에서는 유진 딘킨의 이름을 딴 Dynkin 도표는 어떤 가장자리가 2배 또는 3배(이중 또는 3중 선으로 그려짐)의 그래프의 일종이다. Dynkin 다이어그램은 대수적으로 폐쇄된 분야에 대한 반실행 리알헤브라의 분류, Weyl 그룹과 다른 유한 반사 그룹의 분류, 그리고 다른 맥락에서 발생한다. Dynkin 다이어그램의 다양한 특성(다중 에지 또는 대칭 포함 여부 등)은 관련 Lie 대수학의 중요한 특징에 해당한다.
"Dynkin diagraphy"라는 용어는 모호할 수 있다. 어떤 경우에는 Dynkin 도표를 지시하는 것으로 가정하고, 이 경우에는 루트 시스템과 반단순 리알헤브라에 해당하며, 다른 경우에는 방향을 정하지 않은 것으로 가정하고, 이 경우에는 Weyl 그룹에 해당된다. 이 글에서 "Dynkin diameter"는 지시된 Dynkin diameter를 의미하며, 비방향 Dynkin diameter는 명시적으로 그렇게 명명될 것이다.
반실행 리알헤브라의 분류
Dynkin 다이어그램에 대한 근본적인 관심은 그들이 대수적으로 폐쇄된 분야보다 반실행된 리 알헤브라를 분류하는 것이다. 하나는 그러한 리알헤브라를 그들의 뿌리 시스템을 통해 분류하는데, 이것은 Dynkin 도표로 나타낼 수 있다. 그런 다음 아래에 설명된 대로 Dynkin 도표를 충족해야 하는 제약조건에 따라 분류한다.
그래프 가장자리에 방향을 떨어뜨리는 것은 그것이 생성하는 유한반사군(Weyl group, 소위 Weyl group)에 의해 루트 시스템을 대체하는 것에 해당하며, 따라서 방향을 우회하지 않은 Dynkin 다이어그램은 Weyl 그룹을 분류한다.
그들은 복잡한 숫자에 대해 고전 그룹과 연관된 리 알헤브라와 다음과 같은 서신을 가지고 있다.
- : n+ 1 선형 Lie 대수.
- : + 홀수차원 특수직교 Lie 대수
- : 동정적 리 대수.
- : 짝수차원 특수직교 Lie 대수(> 1
예외 그룹의 경우, Lie 대수학과 관련 Dynkin 도표의 이름이 일치한다.
관련분류
Dynkin 도표는 많은 구별되고 관련 있는 사물을 분류하는 것으로 해석될 수 있으며, 문맥에 따라 "Ann, B, ..."라는 표기법은 그러한 모든 해석을 가리키는 데 사용된다. 이러한 모호성은 혼란스러울 수 있다.
중심 분류는 단순한 Lie 대수학에는 (지향적인) Dynkin 도표와 연관된 루트 시스템이 있다는 것이다. 예를 들어, 이 세 가지 모두를n B라고 할 수 있다.
방향성이 없는 Dynkin 도표는 Coxeter 도표의 한 형태로, 뿌리 시스템과 연관된 유한 반사 그룹인 Weyl 그룹에 해당한다. 따라서 B는n 지향하지 않는 도표(특수 종류의 Coxeter 도표), Weyl 그룹(구체 반사 그룹) 또는 추상 Coxeter 그룹을 가리킬 수 있다.
웨일 집단이 콕시터 집단에 추상적으로 이형화되기는 하지만, 구체적인 이형화는 단순한 뿌리의 순서 선택에 달려 있다. 마찬가지로 Dynkin 다이어그램 표기법이 표준화되어 있는 동안 Coxeter 다이어그램과 그룹 표기법은 다양하고 때로는 Dynkin 다이어그램 표기법에 동의하기도 하며 그렇지 않을 때도 있다.[citation needed]
마지막으로, 때로는 연관된 물체를 동일한 표기법으로 언급하기도 하지만, 이것은 항상 정기적으로 수행될 수는 없다. 예를 들면 다음과 같다.
- E8 격자와 같이 루트 시스템에서 생성된 루트 격자. 이것은 자연적으로 정의되지만 일대일로는 정의되지 않는다. 예를 들어 A와22 G는 모두 육각 격자를 생성한다.
- 연관된 폴리토프 - 예를 들어 고셋 4 폴리토프는21 정점이 E8 루트 시스템에서 파생되고 대칭 그룹으로 E8 Coxeter 그룹을 가지기 때문에 "E8 폴리토프"라고 말할 수 있다.
- 관련된 2차 형태 또는 다지관 – 예를8 들어 E 다지관은 E8 격자에 의해 주어진 교차 형태를 가지고 있다.
이러한 후자의 표기법은 대부분 예외적인 도표와 관련된 물체에 사용되며, 대신 일반 도표(A, B, C, D)와 관련된 물체는 전통적인 명칭을 갖는다.
지수(n)는 다이어그램의 노드 수, 기준의 단순 루트의 수, 루트 시스템의 루트 격자와 스팬의 치수, 콕시터 그룹의 생성자 수, 리 대수 순위와 같다. 그러나 n은 리 대수 정의 모듈(기본 표현)의 치수와는 같지 않다. – Dynkin 다이어그램의 지수를 리혼동해서는 안 된다 지수와 대수상의. 예를 들어 는 2 + = 4에 해당하며, 이는 9차원 공간에 자연스럽게 작용하지만 Lie 대수로서 4위를 가진다.
단순 레이싱된 Dynkin 다이어그램, 다중 에지(A, D, E)가 없는 다이어그램은 더 많은 수학적 객체를 분류한다. ADE 분류에서 토론을 참조한다.
예: }}
예를 들어 기호 2}는 다음을 가리킬 수 있다.
- 2개의 노드가 연결된 Dynkin 다이어그램 , , , 또한 Coxeter 다이어그램으로 해석될 수 있다.
- / 120도) 각도에서 단순 루트가 2개인 루트 시스템.
- Lie 대수 s + = s mathfrak}}={\{sl}_{3 순위 2.
- 뿌리 대칭의 Weyl 그룹(뿌리에 직교하는 하이퍼 평면의 반향), 대칭 그룹 순서 6).
- The abstract Coxeter group, presented by generators and relations,
루트 시스템에서 생성
축소되고 적분된 것으로 가정되는 루트 시스템(또는 "결정론")을 고려한다. 많은 응용에서, 이 뿌리 시스템은 반이행된 리 대수학에서 발생할 것이다. 을(를) 양의 단순 루트의 집합으로 설정하십시오. 그런 다음 에서 도표를 다음과 같이 구성한다.[1] 의 각 요소에 대해 하나의 꼭지점을 가진 그래프를 형성한후 다음 레시피에 따라 각 꼭지점 쌍 사이에 가장자리를 삽입한다. 두 꼭지점에 해당하는 루트가 직교하면 꼭지점 사이에는 에지가 없다. 두 뿌리 사이의 각도가 120도라면 정점 사이에 한쪽 가장자리를 놓는다. 각도가 135도면 가장자리 2개를, 각도가 150도면 가장자리 3개를 넣는다. (이 4가지 경우는 양수 단순근원 쌍 사이의 가능한 모든 각도를 소모한다.)[2] 마지막으로, 주어진 꼭지점 쌍 사이에 가장자리가 있으면 더 긴 뿌리에 해당하는 꼭지점에서 더 짧은 뿌리에 해당하는 꼭지점까지 가리키는 화살표로 장식한다.(뿌리의 길이가 같으면 화살표는 생략한다.) 화살을 "보다 더 큰" 표시로 생각하면 화살이 어느 방향으로 가야 하는지가 분명해진다. Dynkin 도표는 루트 시스템의 분류로 이어진다. 뿌리 사이의 각도와 길이 비율은 관련이 있다.[3] 따라서 비직교적 루트의 가장자리는 길이비 1에 대한 하나의 가장자리, 에 대한 두 의 가장자리 에 대한 세 개의 가장자리로 대안으로 설명할 수 있다와는 상관없이 루트가 직교할 때 가장자리는 없다
오른쪽에 보이는 }}개의 루트 시스템에서는 {\ 및 }라고 표시된 루트가 베이스를 형성한다. 이 두 개의 뿌리가 120도 각(길이비 1)에 있으므로 Dynkin 도표는 단일 에지로 연결된 두 개의 꼭지점으로 구성된다.
제약
Dynkin 다이어그램은 특정 제약조건을 충족해야 한다. 이러한 제약조건은 기본적으로 추가 결정학적 제약조건과 함께 유한 Coxeter-Dynkin 다이어그램에 의해 충족된다.
Coxeter 다이어그램과의 연결
Dynkin 도표는 유한 Coxeter 그룹의 Coxeter 도표와 밀접하게 연관되어 있으며, 용어는 종종 혼동된다.[note 1]
Dynkin 다이어그램은 두 가지 중요한 측면에서 유한 그룹의 Coxeter 다이어그램과 다르다.
- 부분 지시됨
- Dynkin 다이어그램은 부분적으로 방향화되어 있다 – 모든 다중 에지(Coxeter 용어로 "4" 또는 그 이상으로 라벨이 표시됨)는 방향(한 노드에서 다른 노드로 가리키는 화살표)을 가지고 있다. 따라서 Dynkin 다이어그램은 기본 Coxeter 다이어그램(간접 그래프)보다 더 많은 데이터를 가지고 있다.
- 루트 시스템 수준에서 방향은 더 짧은 벡터를 가리키는 것과 일치한다; "3"이라고 표시된 가장자리는 해당 벡터의 길이가 같아야 하기 때문에 방향이 없다. (주의: 일부 저자들은 이 관례를 뒤집으며 화살표가 더 긴 벡터를 향한다.)
- 결정학적 제한
- Dynkin 다이어그램은 허용 가능한 유일한 가장자리 라벨이 2, 3, 4, 6이며, Coxeter 다이어그램에서 공유되지 않는 제한이므로 유한 그룹의 모든 Coxeter 다이어그램이 Dynkin 다이어그램에서 나오는 것은 아니다.
- 뿌리 시스템의 수준에서 이것은 뿌리가 격자를 형성하기 때문에 결정학적 제한 정리에 해당한다.
또 다른 차이점은 Dynkin 다이어그램이 "p"로 표시된 가장자리가 아닌 노드 사이의 이중 또는 삼중 가장자리(p = 4, 6의 경우)로 통상적으로 그려진다는 점이다.
"Dynkin diagraphy"라는 용어는 지시된 그래프를 가리키기도 하고, 때로는 방향을 정하지 않은 그래프를 가리킨다. 정밀도를 위해 이 글에서 "Dynkin diagraphy"는 지시된 것을 의미하며, 밑바탕에 있는 비방향 그래프를 "비방향 Dynkin diagraphy"라고 한다. 그 후 Dynkin 다이어그램과 Coxeter 다이어그램은 다음과 같이 관련될 수 있다.
| 결정학적 | 점군 | |
|---|---|---|
| 연출된 | 딘킨 도표 | |
| 방향이 없는 | 리디렉션되지 않은 Dynkin 도표 | 유한집단의 콕시터 다이어그램 |
이것에 의해 유한집단의 Coxeter 도표는 반사에 의해 생성된 점 그룹에 대응하고, Dynkin 도표는 결정학적 제한 정리에 해당하는 추가 제한을 충족해야 하며, Coxeter 도표는 방향을 정하지 않은 반면 Dynkin 도표는 (부분적으로) 지시된다.
다이어그램에 의해 분류된 해당 수학 물체는 다음과 같다.
| 결정학적 | 점군 | |
|---|---|---|
| 연출된 | 뿌리 시스템 | |
| 방향이 없는 | 웨일 그룹 | 유한 콕시터 군 |
(유한 그룹의) Coxeter 다이어그램이 있는 지시된 그래프에 해당하는 오른쪽 상단의 빈칸은 공식적으로 정의될 수 있지만, 거의 논의되지 않으며, 관심 있는 수학적 객체의 측면에서 단순한 해석을 인정하지 않는 것으로 보인다.
아래에는 Dynkin 다이어그램에서 리디렉션되지 않은 Dynkin 다이어그램까지, 각각 루트 시스템에서 관련 Weyl 그룹까지, 그리고 오른쪽은 Weyl 그룹부터 유한 Coxeter 그룹까지 자연 지도가 있다.
B와n Cn 다이어그램이 동일한 비방향 다이어그램에 매핑되기 때문에 하향 지도는 (정의상) 위에 있지만 1:1은 아니다. 결과 Coxeter 다이어그램과 Weyl 그룹은 BC를n 나타내기도 한다.
오른쪽 지도는 단순히 포용 Coxeter 도표의 –되지 않은 Dynkin 그림 특별한 경우 유한 Coxeter 그룹 –고의 바일 그룹은 특별한 경우도 없에 p, 동시에 모든 Coxeter도 있는 무방향 Dynkin 도표( 빠진 도표 중 H3, H4와 i2(p))5펜스 ≥ 7),고 그에 상응하여 모든 유한 Coxeter.그램oup은 Weyl 그룹이다.
이소모르프스

Dynkin diagrams are conventionally numbered so that the list is non-redundant: for for for 4 {\에 대한 n= 6 그러나 그 패밀리는 도표의 예외적인 이형성과 이에 상응하는 리 알헤브라와 관련 리 그룹의 예외적인 이형성을 산출하는 하위 n에 대해 정의할 수 있다.
간단히 말해서, 은 n= 또는 n= ,에서 가족을 시작할 수 있는데, 이 모든 것은 고유한 빈 다이어그램과 고유한 1-노드 다이어그램이 있기 때문에 이형성이다. 연결된 Dynkin 다이어그램의 다른 이형성은 다음과 같다.
이러한 이형성들은 단순하고 반실현적인 리 알헤브라의 이형성에 대응하며, 이것들의 리 그룹 형태의 특정한 이형성에 대응하기도 한다. 그들은n 또한 E 계열에 맥락을 더한다.[4]
자동형성

다른 도표들 사이의 이형성 외에도, 일부 도표들은 자기 이형성 또는 "자형성"을 가지고 있다. 다이어그램 자동형은 리 대수학의 외부 자동화에 대응하며, 외부 자동모형 그룹 Out = Aut/Inn이 다이어그램 자동모형 그룹과 같다는 것을 의미한다.[5][6][7]
비삼각형 자동화가 있는 다이어그램은 An > Dn(> 1 E이다6. D를4 제외한 이 모든 경우에 비삼각적 자동모형(Out = C2, 순서 2의 주기적 그룹)이 하나 있는 반면, D의4 경우 자동모형 집단은 세 글자(S3, 순서 6)에 대칭 그룹이다 – 이 현상을 "삼각성"이라고 한다. 우연히 이 모든 다이어그램 자동화는 다이어그램이 평면에서 어떻게 전통적인 방식으로 그려지는가의 유클리드 대칭으로 실현될 수 있지만, 이것은 다이어그램이 어떻게 그려지는가에 대한 하나의 유물일 뿐 본질적인 구조가 아니다.
A의n 경우 도표 자동형이 도표인 도표를 반대로 하고 있는데, 이 도표는 선입니다. 에게 i=1,…, n{\displaystyle i=1,\dots ,n}은}나는 Cn{\displaystyle\bigwedge ^{나는}C^{n}⋀ 있(An−1에)의 그림 지수의 노드가 근본적인 추와, 그리고 선도 자기 동형 이중 ⋀에 해당합니다 나는 Cn ↦⋀ n− 나는 Cn.{\displaystyle\bigwedge ^{나는}C^{n}\mapsto\bigwedge ^{n.-i Lie 대수 l l +1,{\ 외측 자동형은 음의 전치, - 이렇게 표현될 수 있다.[6]
D의n 경우, 다이어그램 자동형은 Y의 끝에 있는 두 개의 노드를 전환하고 있으며, 두 개의 키랄 스핀 표현을 전환하는 것과 일치한다. 리 대수 , 으로 실현된 외부 자동형은 결정성 -1과 함께 O(2n)의 행렬에 의해 결합으로 표현될 수 있다. When n = 3, one has so their automorphisms agree, while is disconnected, and the automorphism corresponds to switching the two nodes.
D의4 경우, 근본적인 표현은 두 스핀 표현에 대해 이형이며, 세 글자의 대칭3 그룹(S 또는 순서 6의 다이드랄 그룹 Dih3)은 리 대수의 자동화와 도표의 자동화에 모두 해당한다.
E의6 자동형성군은 도표를 반전시키는 것에 해당하며, 요르단 알헤브라를 사용하여 표현할 수 있다.[6][8]
반시 구현된 리알헤브라에 해당하는 분리 다이어그램은 다이어그램의 구성요소를 교환하는 자동화를 가질 수 있다.
긍정적인 특성에는 추가적인 "다이아그램 자동화"가 있다 – 대략적으로 말하면, 특성 p에서는 다이어그램 자동화를 취할 때 Dynkin 다이어그램의 다중성 p 결합에 있는 화살표를 무시할 수 있다. 반면 특성 3에는 G2의 주문 2자기 동형 그러므로 특성 2에는 B2C2{\displaystyle \mathrm{B}_{2}\cong\mathrm{C}_{2}}와 F4의 ≅ 주문 2자기 동형, 있다.하지만 모든 상황에서. 예를 들어, 그러한 automorphisms 해당 alg의 automorphisms로 발생할 필요가 없는 적용하지 않습니다.Ebraic 그룹, 그러나 오히려 유한한 분야에서 평가된 점의 수준에 있다.
다이어그램 자동화를 통한 Lie 그룹 구축
다이어그램 자동화는 유한 단순 그룹의 분류에서 중심적인 중요성을 갖는 추가 Lie 그룹과 Lie 유형의 그룹을 산출한다.
그들의 Dynkin 도표 관점에서 Chevalley 그룹구성은 고전적인 그룹들, 즉 단일 군집단과 비분할직교 집단들 중 일부를 산출하지 않는다. 스타인버그 그룹은 단일 그룹 A를n 구성하고, 다른 직교 그룹은n D로 구성되는데, 두 경우 모두 도표 자동화와 자기장 자동화를 결합하는 것을 말한다. 이것은 또한 추가적인 이국적인 Lie 그룹 E와6 D를4 산출하는데, 후자는 주문 3 자동형성을 가진 분야에서만 정의된다.
플러스 특성에서의 추가적인 다이어그램 자동화는 스즈키-리 그룹, B2, F4, G를2 산출한다.
접기
(단순히 레이싱) 대칭을 갖는 Dynkin 다이어그램(마인드 또는 아핀)은 대칭에 의해 지수화할 수 있으며, 일반적으로 새로운 곱셈 레이싱 다이어그램을 제공하며, (대칭은 대부분 2-폴드이기 때문에) 접기라고 하는 공정을 가질 수 있다. 리알헤브라의 수준에서 이것은 불변성 아발그라를 외부 자동형성 그룹 아래로 가져가는 것에 해당하며, 그 과정은 도표를 사용하지 않고 순수하게 루트 시스템을 참고하여 정의할 수 있다.[9] 또한 모든 곱셈 레이싱 다이어그램(마인드 또는 무한도)은 레이싱 다이어그램 접기를 통해 얻을 수 있다.[10]
접히는 자동형성에 대한 한 가지 조건은 (자동형성 하의) 동일한 궤도에 있는 그래프의 구별되는 노드가 가장자리로 연결되지 않아야 하며, 루트 시스템의 수준에서 동일한 궤도에 있는 루트는 직교해야 한다는 것이다.[10] 도표 수준에서, 그렇지 않으면 지수 도표는 두 개의 노드를 식별하지만 그 사이에 엣지가 있고 Dynkin 도표에서는 루프가 허용되지 않기 때문에 이것은 필요하다.
인용부("접힌") 다이어그램의 노드와 가장자리는 원래 다이어그램의 노드와 가장자리의 궤도로, 두 개의 입사 모서리가 같은 에지에 매핑되지 않는 한 가장자리는 단일이다(특히 2보다 큰 발랑스 노드에서 맵의 "지점"). 이 경우, 가중치는 입사 가장자리의 수이고 화살표는 N을 가리킨다.ode 사고 지점 - "지점이 비지점 지점으로 매핑". 예를 들어, D4 폴딩에서 G의22 가장자리는 3개의 외부 노드의 클래스(밸런스 1)에서 중앙 노드의 클래스(밸런스 3)까지 가리킨다.
유한 다이어그램의 접힘은 다음과 같다.[11][note 2]
- (A의2n 자동형성은 중간 두 개의 노드가 가장자리로 연결되어 있기 때문에 접히는 것이 아니라 같은 궤도에 있기 때문이다.)
- → 2 }}( 그룹이나 3 사이클에 의한 인지도는 D4→ 에 의한 인지도는 비자발적으로 인지도되는 경우 3가지 방법으로)
부착 다이어그램에는 다음과 같은 유사한 접힘이 존재한다.
접힘의 개념은 Coxeter 다이어그램에도[12] 더 일반적으로 적용될 수 있다. 특히 Dynkin 다이어그램의 허용 오차를 H와n I2(p)에 일반화할 수 있다. 기하학적으로 이것은 균일한 폴리탑의 투영에 해당한다. 특히 모든 단순 레이싱된 Dynkin 도표는 I2(h)로 접을 수 있다. 여기서 h는 Coxeter 평면에 대한 투영에 기하학적으로 해당하는 Coxeter 번호다.
폴딩은 단순히 레이싱된 것에 대한 질문들에 대한 질문을 줄이기 위해 적용될 수 있는데, 이는 레이싱된 Algebras를 직접 곱셈하는 것보다 더 간단할 수 있다. 예를 들어, 이것은 세미임플라이징 Lie Algebras를 구성할 때 할 수 있다. 자세한 내용은 산술 오버플로: 추가 논의를 위해 자동형식으로 접기.
기타 다이어그램 지도
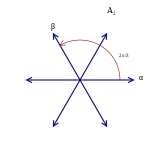 뿌리2 시스템 |  G근계2 |
다이어그램의 일부 추가 지도는 아래와 같이 의미 있는 해석을 가지고 있다. 그러나 모든 루트 시스템 맵이 도표 맵으로 나타나는 것은 아니다.[13]
예를 들어, G에2 있는2 A의 뿌리 시스템을 6개의 긴 뿌리 또는 6개의 짧은 뿌리로 포함하는 두 가지가 있다. 그러나 G2 다이어그램의 노드는 긴 루트 1개와 짧은 루트 1개에 해당하는 반면, A2 다이어그램의 노드는 길이가 같은 루트에 해당하므로 이 루트 시스템 맵은 다이어그램의 맵으로 표현할 수 없다.
루트 시스템의 일부 포함은 다른 도표의 유도 하위 그래프로 표현될 수 있는데, 이는 "노드의 하위 집합, 모든 가장자리 사이에"를 의미한다. 이것은 Dynkin 다이어그램에서 노드를 제거하는 것은 루트 시스템에서 단순 루트를 제거하는 것과 일치하기 때문에, 1등급 이하의 루트 시스템을 산출하기 때문이다. 이와는 대조적으로 노드는 변경하지 않고 엣지를 제거(또는 엣지의 다양성 변경)하는 것은 루트 사이의 각도를 변경하는 것에 해당하므로 루트 시스템 전체를 변경하지 않고는 할 수 없다. 따라서 의미 있게 노드를 제거할 수 있지만 가장자리는 제거할 수 없다. 연결된 다이어그램에서 노드를 제거하면 노드가 리프인 경우 연결된 다이어그램(단순 리 대수) 또는 연결이 끊어진 다이어그램(단순 리 대수)이 생성될 수 있으며, 두 개 또는 세n 개의 성분(D와n E의 경우 후자)이 있다. 리알헤브라의 수준에서 이 포함은 하위 리알헤브라에 해당한다.
최대 서브그래프는 다음과 같다. 다이어그램 자동형성에 의해 관련된 서브그래프는 "콘주게이트"로 표시된다.
- An+1: An, 두 가지 방법으로.
- Bn+1: An, Bn.
- Cn+1: An, Cn.
- Dn+1n: A (2개의 결합 방법), Dn.
- An+1nnn, D, E
- E의6 경우 다음 중 두 가지가 일치한다. 은(는) 결합형이다.
- F4: B3, C3.
- G2: A1, (긴 뿌리 또는 짧은 뿌리로서) 두 가지 비콘주게이트 방식으로.
마지막으로, 다이어그램의 이중성은 화살표 방향을 반대로 하는 것에 해당한다.[13] B와n C는n 이중이고, F와42 G는 단순 레이싱 ADE 다이어그램과 마찬가지로 자가 이중이다.
단순 레이싱

다중 가장자리가 없는 Dynkin 도표를 Lie 대수 및 Lie 그룹과 같이 간단히 레이싱이라고 한다. 이것들은 , , 다이어그램이며, 그러한 다이어그램이 분류하는 현상을 ADE 분류라고 한다. 이 경우 Dynkin 다이어그램은 복수의 가장자리가 없기 때문에 Coxeter 다이어그램과 정확히 일치한다.
사타케 도표
Dynkin 다이어그램은 복잡한 반실행 리알헤브라를 분류한다. 실제 반실행 리알헤브라는 복잡한 반실행 리알헤브라의 실제 형태로 분류될 수 있으며, 이것들은 사타케 도표에 의해 분류되는데, 일정한 규칙에 따라 어떤 정점을 검정(충분)으로 표시하고 다른 정점을 화살표로 쌍으로 연결하여 얻은 것이다.
역사
Dynkin 다이어그램은 Semisimple Li Algebras의 분류를 단순화하는 두 개의 논문(1946, 1947년)에서 사용했던 유진 Dynkin의 이름을 따서 명명되었다;[14] (Dynkin 2000) (을 참조하라. 당시 반역죄나 다름없던 1976년 딘킨이 소련을 떠나자 소련의 수학자들은 그의 이름을 쓰기보다는 '단순한 뿌리의 다이어그램'을 언급하라는 지시를 받았다.[citation needed]
비방향 그래프는 Coxeter(1934)에 의해 반사 그룹을 분류하기 위해 이전에 사용되었었다. 여기서 노드는 단순한 반사에 대응하고, 그래프는 오늘날 사용되는 것처럼 단순 루트에 해당하는 노드와 함께 루트 시스템을 기준으로 Witt(1941)에 의해 사용되었다.[14][15] 그 후 Dynkin은 1946년과 1947년에 그것들을 사용했고, 1947년 논문에서 Coxeter와 Witt를 인정했다.
관습
Dynkin 도표를 여러가지 방법으로;그 전당 대회 여기를 따라 일반적이다, 원자가 2의 노드에 180도 각도, 데카넴의 원자가 3노드에서 120°각도, 앙의 원자가 3노드에서 90°/90°/180° 각도로 다양한 1,2또는 3병렬 가장자리에 의해 지시되고, 루트[15]길이 가장자리에 화살 그림에 표시된 파생하다.orientation. 단순성을 넘어, 다이어그램 자동화는 다이어그램의 유클리드 등각도에 의해 실현된다는 것이 이 관습의 또 다른 이점이다.
대안적 관례로는 다중성(Coxeter 다이어그램에서 일반적으로 사용됨), 루트 길이를 나타내기 위해 노드를 어둡게 하거나 노드가 더 뚜렷하게 구별되도록 Valence 2 노드에 120° 각도를 사용하는 것이 있다.
노드 번호 매기기에 관한 규정도 있다. 가장 일반적인 현대적 관습은 1960년대에 개발되었고 (Bourbaki 1968년)에 설명되어 있다.[15]
순위 2 Dynkin 다이어그램
Dynkin 도표는 일반화된 Cartan 도표와 동일하며, 2x2 Cartan 도표와 2등급 Dynkin 도표의 표에 나타나 있다.
순위 2의 경우 카르탄 행렬 형식은 다음과 같다.
다중 에지 다이어그램은 비대각 카르탄 행렬21 요소 -a12, -a에 해당하며, 가장자리 수는 최대(-a21, -a12)와 같고 화살표는 비일관성 요소를 가리킨다.
일반화된 카르탄 행렬은 다음과 같은 정사각형 행렬 =( ) A이다.
- 대각선 항목의 경우 = }
- 대각선이 아닌 항목의 경우
- = 인 경우에만 j =
카르탄 행렬은 집단이 유한 유형(양-확정 행렬인 경우, 즉 모든 고유값이 양인 경우), 아핀 유형(양-확정성이 아닌 양-세미드 핀라이트인 경우, 즉 모든 고유값이 음이 아닌 경우) 또는 무기한 유형인지 여부를 결정한다. 무기한 유형은 종종 더 세분화된다. 예를 들어, Coxeter 그룹이 하나의 음의 고유값을 가지고 있고 다른 모든 고유값을 양수인 경우 Lorenzian이다. 더욱이 복수의 출처는 히버볼릭 콕시터 집단을 가리키지만, 이 용어에 대한 몇 가지 비등등등한 정의가 있다. 아래 논의에서 쌍곡선 콕시터 그룹은 로렌츠인의 특수한 경우로서 여분의 조건을 만족시킨다. 순위 2의 경우 모든 부정 결정 요인 카르탄 행렬은 쌍곡선 Coxeter 그룹에 해당한다. 그러나 일반적으로 대부분의 부정적인 결정인자 행렬은 쌍곡선도 로렌츠도 아니다.
유한 가지는 (-a21, -a12)=(1,1), (2,1), (3,1)를 가지며, 부속 가지(영점 결정인자)는 (-a21, -a12) = (2,2) 또는 (4,1)를 가진다.
| 그룹 이름을 붙이다 | 딘킨 도표 | 카르탄 행렬 | 대칭 주문 | 관련 단순 레이스의 무리를3 짓다 | |||
|---|---|---|---|---|---|---|---|
| (표준) 다의의 도표를 찍다 | 가치있는 도표를1 찍다 | 콕시터 도표를2 찍다 | 결정인자 (4-a21*a12) | ||||
| 유한(결정)0 | |||||||
| 악사11 | 4 | 2 | |||||
| A을2 (간접적) | 3 | 3 | |||||
| B2 | 2 | 4 | | ||||
| C2 | 2 | 4 | | ||||
| 기원전2 (간접적) | 2 | 4 | |||||
| G2 | 1 | 6 | | ||||
| G2 (간접적) | 1 | 6 | |||||
| 아핀 (결정=0) | |||||||
| A을1(1) | 0 | ∞ | | ||||
| A을2(2) | 0 | ∞ | | ||||
| 쌍곡선(결정력<0) | |||||||
| -1 | - | ||||||
| -2 | - | ||||||
| -2 | - | ||||||
| -3 | - | ||||||
| -4 | - | ||||||
| -4 | - | ||||||
| -5 | - | ||||||
| 4시 5분 | - | ||||||
| 참고1: 쌍곡선 그룹 (a12*a21>4)의 경우, 가장자리에 명시적인 라벨링(a21, a12)을 선호하여 멀티에지 스타일을 포기한다. 이것들은 보통 유한하고 첨부된 그래프에는 적용되지 않는다.[16] 참고2: 리디렉션되지 않은 그룹의 경우 Coxeter 다이어그램을 교환할 수 있다. 그것들은 대칭의 순서에 의해 라벨이 붙여지고, 순서 3은 라벨이 없는 것을 암시한다. 참고3: 많은 다중 에지 그룹은 적절한 폴딩 작업을 적용하여 순위가 높은 단순 레이싱 그룹에서 얻을 수 있다. | |||||||
유한 다이닝킨 도표
| 순위 | 클래식 리 그룹 | 예외적인 Lie | ||||
|---|---|---|---|---|---|---|
| }} / | ||||||
| 1 | A을1 | |||||
| 2 | A을2 | B2 | C2=B2 | D2=A1A1 | G2 | |
| 3 | A을3 | B3 | C3 | D3=A3 | E3=A2A1 | |
| 4 | A을4 | B4 | C4 | D4 | E4=A4 | F4 |
| 5 | A을5 | B5 | C5 | D5 | E5=D5 | |
| 6 | A을6 | B6 | C6 | D6 | E6 | |
| 7 | A을7 | B7 | C7 | D7 | E7 | |
| 8 | A을8 | B8 | C8 | D8 | E8 | |
| 9 | A을9 | B9 | C9 | D9 | ||
| 10+ | .. | .. | .. | .. | ||
아핀 딘킨 도표
Dynkin 도표의 확장, 즉 appine Dynkin 도표가 있다; appine Li Algebras의 카르탄 행렬을 분류한다. 이러한 오류는 (Kac 1994, 제4장 47–) 대상 ( 특별히 (Kac 1994, 페이지 53–55) 오류: 없음:(에 분류된다. Affine diagrams are denoted as or where X is the letter of the corresponding finite diagram, and the exponent depends on which series of affine diagrams they are in. 이 중 첫 번째, () , 이 가장 흔하며, 확장 Dynkin 다이어그램으로 불리며 tild로 표시되며, 때로는 + 위첨자로 표시되기도 한다.[17] ~ = ( 1)= + . (2)와 (3) 시리즈를 꼬임 아핀 도표라고 한다.
다이어그램은 Dynkin 다이어그램 생성기를 참조하십시오.
 노드가 녹색으로 추가된 확장 아핀 Dynkin 다이어그램 세트( 의 경우 3 3 의 경우 4 | 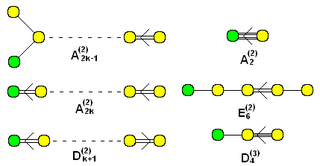 "뒤틀린" 부속서식은 (2) 또는 (3) 위첨자로 이름 지어진다. (첨자 k는 항상 그래프의 노란색 노드 수를 계산한다. 즉, 총 노드 수를 1에서 뺀다.) |
최대 10개 노드까지 어핀 그룹에 대한 Dynkin 그래프는 모두 여기에 있다. 확장 Dynkin 그래프는 위의 유한 그래프와 동일한 ~ 패밀리로 주어지며, 한 노드가 추가된다. 다른 지시 그래픽 변형은 상위 순서의 그룹 접기를 나타내는 위첨자 값 (2) 또는 (3)과 함께 제공된다. 이것들은 비틀린 아핀 도표로 분류된다.[18]
쌍곡선 및 상위 Dynkin 다이어그램
콤팩트 및 비컴팩트 쌍곡선 Dynkin 그래프 세트가 열거되었다.[19] 모든 3위 쌍곡선 그래프는 작다. 컴팩트 쌍곡선 Dynkin 다이어그램은 순위 5까지 존재하며, 비 컴팩트 쌍곡선 그래프는 순위 10까지 존재한다.
| 순위 | 작은 | 비컴팩트 | 합계 |
|---|---|---|---|
| 3 | 31 | 93 | 123 |
| 4 | 3 | 50 | 53 |
| 5 | 1 | 21 | 22 |
| 6 | 0 | 22 | 22 |
| 7 | 0 | 4 | 4 |
| 8 | 0 | 5 | 5 |
| 9 | 0 | 5 | 5 |
| 10 | 0 | 4 | 4 |
콤팩트 쌍곡선 Dynkin 다이어그램
| 3위 | 4위 | 5위 | |
|---|---|---|---|
선형 그래프
| 순환 그래프
|
|
|
비컴팩트(과다 확장된 양식)
M 이론과 같이 이론 물리학에 사용되는 일부 표기법은 "~" 대신 확장 그룹에 "+" 위첨자를 사용하며, 이를 통해 더 높은 확장 그룹을 정의할 수 있다.
- 확장 Dynkin 다이어그램(affine)에는 "+"가 부여되며, 추가된 하나의 노드를 나타낸다. ("~"와 동일)
- 과도하게 확장된 Dynkin 다이어그램(하이퍼볼릭)에는 "^" 또는 "+"가 부여되며 추가된 두 개의 노드를 나타낸다.
- 3개의 노드가 추가된 매우 확장된 Dynkin 다이어그램에는 "++"가 주어진다.
| 순위 | n-2(1)^ = A | n-2(1)^ = B | Cn-2(1)^ | n-2(1)^ = D | E / F / G |
|---|---|---|---|---|---|
| 3 | | ||||
| 4 | 4 | C2(1)^ A을4(2)'^ A을4(2)^ D3(2)^ | G2(1)^ D4(3)^ | ||
| 5 | | C3(1)^ A을6(2)^ A을6(2)'^ D5(2)^ | |||
| 6 | C4(1)^ A을8(2)^ A을8(2)'^ D7(2)^ | F4(1)^ E6(2)^ | |||
| 7 | |||||
| 8 | E6(1)^ | ||||
| 9 | E7(1)^ | ||||
| 10 | =E8(1)^ |
238 쌍곡선 그룹(콤팩트 및 비컴팩트)
n 3 의 238 쌍곡선 그룹(컴팩트 및 비컴팩트)은 ) 로 명명되고 i= ,,각 계급마다
매우 확장된
매우 확장된 그룹은 로렌츠 그룹으로, 유한한 그룹에 3개의 노드를 추가하여 정의된다. E8, E7, E6, F4, G는2 매우 확장된 그룹으로 끝나는 6개의 시리즈를 제공한다. 표시되지 않은 다른 확장 영상 시리즈는 An, Bn, Cn, D에서n 각 n에 대해 다른 영상 시리즈로 정의할 수 있다. 관련 카르탄 행렬의 결정요인은 시리즈가 유한(양)에서 아핀(영)으로 변화하고 비콤팩트 쌍곡군(음)으로 변화하며, 하나의 시간적 차원을 사용하여 정의할 수 있는 로렌츠 그룹으로 끝나는 위치를 결정하며, M 이론에 사용된다.[20]
| 유한한 | |||
|---|---|---|---|
| 2 | A을2 | C2 | G2 |
| 3 | A2+= ~ }} | C2+= ~ }} | G2+= ~ }} |
| 4 | A을2++ | C2++ | G2++ |
| 5 | A을2+++ | C2+++ | G2+++ |
| 데트(Mn) | 3(3-n) | 2(3-n) | 3-n |
| 유한한 | |||||||
|---|---|---|---|---|---|---|---|
| 4 | B3A1 | A3A1 | A을22 | ||||
| 5 | A을5 | D5 | B4A1 | D4A1 | A을5 | ||
| 6 | A5+= ~ | B5+= ~ | D5+= ~ | A을6 | B6 | D6 | E6 |
| 7 | A을5++ | B5++ | D5++ | A6+= ~ | B6+= ~ | D6+= | E6+= ~ |
| 8 | A을5+++ | B5+++ | D5+++ | A을6++ | B6++ | D6++ | E6++ |
| 9 | A을6+++ | B6+++ | D6+++ | E6+++ | |||
| 데트(Mn) | 6(6-n) | 2(6-n) | 4(6-n) | 7(7-n) | 2(7-n) | 4(7-n) | 3(7-n) |
| 유한한 | A을7 | B7 | D7 | E7 | E8 |
|---|---|---|---|---|---|
| 3 | E3=A2A1 | ||||
| 4 | A3A1 | E4=A4 | |||
| 5 | A을5 | E5=D5 | |||
| 6 | B5A1 | D5A1 | D6 | E6 | |
| 7 | A을7 | B7 | D7 | E7 | E7 |
| 8 | A7+= ~ | B7+= ~ | D7+= | E7+= ~ | E8 |
| 9 | A을7++ | B7++ | D7++ | E7++ | E9=E8+= ~ |
| 10 | A을7+++ | B7+++ | D7+++ | E7+++ | E10=E8++ |
| 11 | E11=E8+++ | ||||
| 데트(Mn) | 8(8-n) | 2(8-n) | 4(8-n) | 2(8-n) | 9-n |
참고 항목
| 위키미디어 커먼즈에는 딘킨 도표와 관련된 미디어가 있다. |
- 사타케 도표
- 수정 불가능한 Tits 지수 목록
- Klasifikation von Wurzelsystemen(루트 시스템 분류)(독일어)
메모들
인용구
- ^ 홀 2015 8.6
- ^ 홀 2015 제안 8.6 및 8.13
- ^ 홀 2015 제안 8.6
- ^ Baez, John (April 13, 1998), This Week's Finds in Mathematical Physics (Week 119)
- ^ Fulton & Harris 1991, 발의안 D.40
- ^ a b c 간단한 리 알헤브라의 외형 자동화
- ^ 험프리스 1972, § 16.5
- ^ 제이콥슨 1971, § 7
- ^ 대수 기하학 및 숫자 이론: 블라디미르 드린펠트의 50번째 생일을 기념하여, 빅터 긴츠부르크가 편집한, 섹션 3.6: 클러스터 접기
- ^ a b 자동식 폴딩 2016-03-04년 웨이백머신, 존 스템브리지, 4pp, 79K, 2008년 8월 20일, 존 스템브리지의 기타 기사
- ^ 이러한 접힘과 참고문헌의 그림은 Stekolshchik 2008, 페이지 102의 주석 5.4를 참조한다.
- ^ Zuber, Jean-Bernard (1997). "Generalized Dynkin diagrams and root systems and their folding": 28–30. CiteSeerX 10.1.1.54.3122. Cite 저널은 필요로 한다.
journal=(도움말) - ^ a b Armstrong, John (March 5, 2010). "Transformations of Dynkin Diagrams".
- ^ a b Knapp 2002, 페이지 758
- ^ a b c Dynkin 다이어그램 E6, E7, E8은 왜 항상 그려진 방식으로 그려지는가?
- ^ 섹션 2.1인치
- ^ 예를 참조하십시오.
- ^ Kac, Victor G. (1990). "4. A Classification of Generalized Cartan Matrices". Infinite-Dimensional Lie Algebras. Cambridge University Press. pp. 53–. ISBN 978-0-521-46693-6.
- ^ Carbone, Lisa; Chung, Sjuvon; Cobbs, Leigh; McRae, Robert; Nandi, Debajyoti; Naqvi, Yusra; Penta, Diego (2010). "Classification of hyperbolic Dynkin diagrams, root lengths and Weyl group orbits". Journal of Physics A: Mathematical and Theoretical. 43 (15): 155209. arXiv:1003.0564. Bibcode:2010JPhA...43o5209C. doi:10.1088/1751-8113/43/15/155209.
- ^ Englert, François; Houart, Laurent; Taormina, Anne; West, Peter (2003). "The symmetry of M-theories". Journal of High Energy Physics. 2003 (9): 020. arXiv:hep-th/0304206. Bibcode:2003JHEP...09..020E. doi:10.1088/1126-6708/2003/09/020.
참조
- Dynkin, E. B. (1947), "The structure of semi-simple algebras .", Uspekhi Mat. Nauk, N.S. (in Russian), 2 (4(20)): 59–127
- Bourbaki, Nicolas (1968), "Chapters 4–6", Groupes et algebres de Lie, Paris: Hermann
- Jacobson, Nathan (1971-06-01), Exceptional Lie Algebras, CRC Press, ISBN 978-0-8247-1326-3
- Humphreys, James E. (1972), Introduction to Lie Algebras and Representation Theory, Birkhäuser, ISBN 978-0-387-90053-7
- Fulton, William; Harris, Joe (1991). Representation theory. A first course. Graduate Texts in Mathematics, Readings in Mathematics. 129. New York: Springer-Verlag. doi:10.1007/978-1-4612-0979-9. ISBN 978-0-387-97495-8. MR 1153249. OCLC 246650103.
- Dynkin, Evgeniĭ Borisovich; Alexander Adolph Yushkevich; Gary M. Seitz; A. L. Onishchik (2000), Selected papers of E.B. Dynkin with commentary, AMS Bookstore, ISBN 978-0-8218-1065-1
- Hall, Brian C. (2015), Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, Graduate Texts in Mathematics, 222 (2nd ed.), Springer, ISBN 978-3319134666
- Knapp, Anthony W. (2002), Lie groups beyond an introduction (2nd ed.), Birkhäuser, ISBN 978-0-8176-4259-4
- Stekolshchik, R. (2008), Notes on Coxeter Transformations and the McKay Correspondence, Springer Monographs in Mathematics, arXiv:math/0510216, doi:10.1007/978-3-540-77399-3, ISBN 978-3-540-77398-6











 해당하며, 이는
해당하며, 이는



















 대한 n
대한 n
















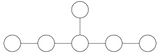





 의한 인지도는 비자발적으로 인지도되는 경우 3가지 방법으로)
의한 인지도는 비자발적으로 인지도되는 경우 3가지 방법으로)




 (는) 결합형이다.
(는) 결합형이다.

![A=\left[{\begin{matrix}2&a_{12}\\a_{21}&2\end{matrix}}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f0c38b6f92dd343e402c1f09e8a077371712646)



 경우에만 j =
경우에만 j = ![\left[{\begin{matrix}2&a_{12}\\a_{21}&2\end{matrix}}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/609b9b4324da49c4903330c430b14203d6f971cb)
![\left[{\begin{smallmatrix}2&0\\0&2\end{smallmatrix}}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/58d402f7fd38428fe2ac791f5a5d12bf7832c69f)
![\left[{\begin{smallmatrix}2&-1\\-1&2\end{smallmatrix}}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/18cb26b504d63dba11f3a12c7ee8fa25fe3bdf0a)
![\left[{\begin{smallmatrix}2&-2\\-1&2\end{smallmatrix}}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/07ca67f2863fd2e6f5a6d91133f30d43a1c95805)

![\left[{\begin{smallmatrix}2&-1\\-2&2\end{smallmatrix}}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a86fb5415f60aea3cee78429d52d340fc1df9ab)
![\left[{\begin{smallmatrix}2&-{\sqrt {2}}\\-{\sqrt {2}}&2\end{smallmatrix}}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/934421fb85592c1788a92b7d350953dd2ca94b5e)
![\left[{\begin{smallmatrix}2&-1\\-3&2\end{smallmatrix}}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/8008c32cde8626798763d8c84924571bffad4812)

![\left[{\begin{smallmatrix}2&-{\sqrt {3}}\\-{\sqrt {3}}&2\end{smallmatrix}}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b77e92921199a57f051014d4938de1a0d22ef38)
![\left[{\begin{smallmatrix}2&-2\\-2&2\end{smallmatrix}}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd86323eaf497d2bb96f757556dd458abd5863cf)

![\left[{\begin{smallmatrix}2&-1\\-4&2\end{smallmatrix}}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ee764ce2933d720bd85ab4f4425789a0452bb97)

![\left[{\begin{smallmatrix}2&-1\\-5&2\end{smallmatrix}}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5f8667328ef032fcc28485f9498d0aa472592ef)
![\left[{\begin{smallmatrix}2&-2\\-3&2\end{smallmatrix}}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/de5c1b92cef68df449f22b4667b47f409865b4a9)
![\left[{\begin{smallmatrix}2&-1\\-6&2\end{smallmatrix}}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/209a341193290b49c172a7b764b7c280f8a4e95e)
![\left[{\begin{smallmatrix}2&-1\\-7&2\end{smallmatrix}}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/13892cd6e699b3c266c6f2c5155a7d3a81171728)
![\left[{\begin{smallmatrix}2&-2\\-4&2\end{smallmatrix}}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/3373a4f62ccb77cbfad04b43f2a9b57dc7fdc618)
![\left[{\begin{smallmatrix}2&-1\\-8&2\end{smallmatrix}}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/457a113c8f8ee31dbb097965abe5da05593e254b)
![\left[{\begin{smallmatrix}2&-3\\-3&2\end{smallmatrix}}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/58de83867bd03b11edff1e45a0f03073a287b066)
![\left[{\begin{smallmatrix}2&-b\\-a&2\end{smallmatrix}}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6f2eb2e6d752a7d458a6c9892cee665463ab8fa)








 가장 흔하며, 확장 Dynkin 다이어그램으로 불리며
가장 흔하며, 확장 Dynkin 다이어그램으로 불리며 




























































































































