삼각형의 꼭짓점을 통과하는 원
기하학 에서 삼각형 의 외접원 또는 원은 세 개 의 꼭짓점을 모두 통과하는 원 입니다.이 원의 중심을 삼각형의 원주 중심이라고 하며, 그 반지름을 원주 반지름이라고 합니다. 원주 중심은 삼각형의 변에서 세 개의 수직 이등분선 사이의 교차점 이며 삼각형 중심입니다.
보다 일반적으로, 모든 꼭짓점이 동일한 원 위에 있는 n변 다각형을 외접원이라고도 하며 , 특별 4 에서는 순환 사각형이라고도 합니다. 모든 직사각형 , 이등변 사다리꼴 , 오른쪽 연 및 일반 다각형은 순환하지만 모든 다각형이 순환하는 것은 아닙니다.
직선자 및 나침반 구조 삼각형 중심 Q의 구축 삼각형의 원주 중심은 세 개의 수직 이등분선 중 두 개를 그려서 구성 할 수 있습니다. 세 개의 비공선 점의 경우 이 두 선은 평행할 수 없으며 원주 중심이 교차하는 점입니다. 이등분선의 모든 점은 이등분선이 나누는 두 점에서 등거리이며, 여기서 두 이등분선의 이 점은 세 개의 삼각형 꼭짓점 모두에서 등거리입니다. 원주 반경은 원주에서 세 개의 정점까지의 거리입니다.
대체 시공 원주 중심의 대체 시공(파선 교차점) 원주 중심을 결정하는 다른 방법은 정점 중 하나에서 출발하는 두 개의 선을 공통된 면과 각도로 그리는 것입니다. 공통 출발 각도는 90°에서 반대쪽 정점의 각도를 뺀 것입니다. (반대쪽 각도가 둔할 경우, 음의 각도로 선을 그리는 것은 삼각형 밖으로 나가는 것을 의미합니다.)
해안 항해 에서 삼각형의 원은 때때로 나침반이 없을 때 육분사 를 사용하여 위치선 을 얻는 방법으로 사용됩니다.두 랜드마크 사이의 수평 각도는 관찰자가 누워 있는 원을 정의합니다.
원주 방정식 데카르트 좌표 유클리드 평면에서, 내접 삼각형의 꼭짓점의 데카르트 좌표 로 원의 방정식을 명시적으로 제공할 수 있습니다.라고 가정합니다.
A = ( A x , A y ) B = ( B x , B y ) C = ( C x , C y ) 디스플레이{style{aligned}\mathbf {A} &=(A_{x}, A_{y}\\\mathbf {B} & =(B_{x},B_{y})\\\mathbf {C} & =(C_{x},C_{y})\end{aligned}}} 점 A, B, C 의 좌표입니다.그 다음 원은 방정식을 만족하는 데카르트 평면에서 점 v = v v displaystyle \mathbf {v} v_{x,v_{y})
v − u 2 = r 2 A − u 2 = r 2 B − u 2 = r 2 C − u 2 = r 2 표시 \style \mathbf {v} -\mathbf {u} ^{2}&=r^{2} -\mathbf {A} -\mathbf {u} ^{2} ^{2} ^{2} -\mathbf {C} -\mathbf {u} ^{2} ^{2} ={2} \mathbf} \end {{} 점 A ,B ,C ,v 중심 u 동일 한 거리 r임을 보장합니다. 편광 동일성을 사용하여, 이 방정식들은 행렬이 다음 과 같은 조건으로 감소합니다.
[ v 2 − 2 v x − 2 v y − 1 A 2 − 2 A x − 2 A y − 1 B 2 − 2 B x − 2 B y − 1 C 2 − 2 C x − 2 C y − 1 ] 표시({stylebegin{bmatrix} \mathbf {v} ^{2}&-2v_{x}&-2v_{y}&-1\\mathbf {A} ^{2}&-2A_{y}&-1\mathbf {B} ^{2}&2B_{x}&-1\mathbf{C_{C} ^2} 0 이 아닌 커널이 있습니다.따라서 원주는 이 행렬의 행렬식 의 0의 궤적 으로 설명할 수 있습니다.
디트 [ v 2 v x v y 1 A 2 A x A y 1 B 2 B x B y 1 C 2 C x C y 1 ] = 0. 표시 스타일 \det \begin{bmatrix} \mathbf {v} ^{2}&v_{x}&1\\\mathbf {A} ^{2}&A_{x}& A_{y}&1\\ \mathbf {B}^{2}&B_{x}&B_{y}&1\\\mathbf {C}^{2}&C_{x}&C_{y}&1\end{bmatrix}}=0. 보조 인자 확장을 사용하여 다음과 같이 합니다.
S x = 1 2 디트 [ A 2 A y 1 B 2 B y 1 C 2 C y 1 ] , S y = 1 2 디트 [ A x A 2 1 B x B 2 1 C x C 2 1 ] , a = 디트 [ A x A y 1 B x B y 1 C x C y 1 ] , b = 디트 [ A x A y A 2 B x B y B 2 C x C y C 2 ] 스타일 표시({{aligned}) S_{x}&=mathfrac{1}{2}}\det{{{\bmatrix} \mathbf {A}^{2}& A_{y}&1\\ \mathbf {B}^{2}&B_{y}&1\\\\mathbf {C}^{2}&C_{y}&1\end{bmatrix},\[5pt] S_{y}&=nbfrac{1}{2}}\det{{{bmatrix} A_{x}& \mathbf {A}^{2}&1\B_{x}& \mathbf {B}^{2}&1\C_{x}& \mathbf {C}^{2}&1\end{bmatrix},\[5pt]a&=\det{bmatrix} A_{x}&A_{y}&1\\B_{x}&B_{y}&1\C_{x}&1\end{bmatrix},\[5pt]b&=\det{bmatrix} A_{x}&A_{y}& \mathbf {A}^{2}\B_{x}&B}&\mathbf {B}^{2}\C_{x}&C_{y}& \mathbf {C}^{2}\end{bmatrix}}\end{aligned}}} 그런 다음 v2 - 2Sv - b = 0{{displaystyle a \mathbf {v} ^{2}-2\mathbf {Sv} -b=0}을 가지며, 여기서 S = (Sx, Sy), {\displaystyle \mathbf {S} = (S_{x, S_{y}), 그리고 세 점들이 한 줄에 있지 않다고 가정할 때, 즉, 즉, 두 개의 점들이 S 2개의 점들이 S -D에서 일반화된 원을 갖는 선으로 볼 수 있다 isplaystyle \left \mathbf {v} -{\tfrac \mathbf {S}{a}}\right ^{2}=tfrac {\mathbf {b}}+{\tfrac {\mathbf{S}^{2}}^{a^{2}}}로, 둘레 중심 S에 표시 스타일 A를 부여한다. 유사한 접근법을 통해 사면체 의 둘레 방정식을 추론할 수 있습니다
모수 방정식 원 을 포함하는 평면에 수직인 단위 벡터 는 다음과 같이 주어진다.
n ^ = ( P 2 − P 1 ) × ( P 3 − P 1 ) ( P 2 − P 1 ) × ( P 3 − P 1 ) . {\stylewidehat {n}}을(를) 표시합니다. = netfrac {(P_{2}-P_{1})\times(P_{3}-P_{1})}{(P_{2}-P_{1})}}. 따라서 반지름, r, 중심, Pc, 원 위의 점, P0 및 원을 포함하는 평면의 법선 단위 n^, {\displaystyle {\widehat {n}}을 고려할 때, n^{\displaystyle {n}에 대해 양의 방향(즉, 오른손 방향)으로 진행되는 원의 매개변수 방정식은 다음과 같다:
R ( s ) = P c + 코스 ( s r ) ( P 0 − P c ) + 죄악 ( s r ) [ n ^ × ( P 0 − P c ) ] . (\displaystyle \mathrm {R}(s)=\mathrm {P_{c}} +\cos \left\frac {\mathrm {r}}{\right)(P_{0}-P_{c})+\sin \left\frac {\mathrm {rm {r}}}\right)\left[\wide{ntimes {{p}(P_0}(P_right}}}}}({c}\c}}] 삼선 및 무게중심 좌표 삼각 좌표 x : y : z : x + x + x + cz = 0.{\displaystyle{tfrac{a}}+{\tfrac{b}}+{\tfrac{c}{z}=0.} 무게 중심 좌표 x : z는 2 + 2 + 2 + 2 + cz = 0.{\frac{tfrac{tfrac{t^2}}를 나타낸다
원주의 등각 공역 은 x x cz = 0 3선 좌표와 = displaystyle y z 0 .{displaystyle z 0.}
고차원 또한 일반화된 방법을 사용하여 d차원에 포함 된 삼각형의 원주를 찾을 수 있습니다. A, B ,C 합니다 시스템을 원점에 C를 배치
a = A − C , b = B − C . 표시({style\mathbf {a} &=\mathbf {A} -\mathbf {C},\\mathbf {b} &=\mathbf {B} -\mathbf {C} .\end{aligned}) 원주율 은 다음과 같습니다.
r = ‖ a ‖ ‖ b ‖ ‖ a − b ‖ 2 ‖ a × b ‖ = ‖ a − b ‖ 2 죄악 θ = ‖ A − B ‖ 2 죄악 θ , {\displaystyle r={\mathfrac {a} \right\left\mathbf {b} \right\left\mathbf {a} -\mathbf {a} \ta \right\}={\mathbf} \right \\ta \mathbf} \right \right \mathbfraight = \mathbfraight \bfraight {\bf} \mathbf} \mathbfraft \mathbf} \\bf} \bf{{{\ 여기서 θ 는 a 사이 원주 중심 p 0 다음과 같이 주어진다.
p 0 = ( ‖ a ‖ 2 b − ‖ b ‖ 2 a ) × ( a × b ) 2 ‖ a × b ‖ 2 + C . {\displaystyle p_{0}=displaystyle p_{0}\right\^{2}\mathbf {b} -\left\mathbf {b}\times (\mathbf {a} \times \mathbf {a)}{2\left\\mathbf {a} \times \mathbf{a}\right\}+{C}\mathbf{C}. 이 공식은 교차곱이 다른 차원에서 정의되지 않기 때문에 3차원에서만 작동하지만 교차곱을 다음과 같은 동일성으로 대체하여 다른 차원으로 일반화할 수 있습니다.
( u × v ) × w = ( u ⋅ w ) v − ( v ⋅ w ) u , u × ( v × w ) = ( u ⋅ w ) v − ( u ⋅ v ) w , ‖ u × v ‖ 2 = ‖ u ‖ 2 ‖ v ‖ 2 − ( u ⋅ v ) 2 . 표시(\style{\mathbf {u} \times \mathbf {v})\times \mathbf {w} &=(\mathbf {u} \cdot \mathbf {w} )\mathbf {v} -(\mathbf {v} \mathbf {u} \times \mathbf{w} \mathbf} \mathbf} \mathbf{w} \mathbf} \mathbf} \mathbf} \mathbf} \m \\left\\mathbf {u} \times \mathbf {v} \right\^{2}&=\left\\mathbf {u} \right\^{2}\left\mathbf {v} \right\^{2}-(\mathbf {u} \cdot \mathbf {v})^{2}. \end{aligned}}} 둘레 중심 좌표 데카르트 좌표 원주 중심 = U Y ){ displaystyle left(U_{x}, U_{y}\right)} 데카르트 좌표는
U x = 1 D [ ( A x 2 + A y 2 ) ( B y − C y ) + ( B x 2 + B y 2 ) ( C y − A y ) + ( C x 2 + C y 2 ) ( A y − B y ) ] U y = 1 D [ ( A x 2 + A y 2 ) ( C x − B x ) + ( B x 2 + B y 2 ) ( A x − C x ) + ( C x 2 + C y 2 ) ( B x − A x ) ] 스타일 표시({{aligned}) U_{x}&=nbfrac{1}{D}}\left[(A_{x}^{2}+ A_{y}^{2}(B_{y}-C_{y})+(B_{x}^{2}+B_{y}^{2})(C_{y}-A_{y})+(C_{x}^{2}+C_{y}^{y})(A_{y}-B_{y}\right]\ \[5pt]U_{y}&=nbfrac{1}{D}}\left[(A_{x}^{2}+ A_{y}^{2}(C_{x}-B_{x})+(B_{x}^{2}+B_{y}^{2}(A_{x}-C_{x})+(C_{x}^{2}+C_{y}^{2})(B_{x}-A_{x}\right{x}})\end{}}} 와 함께
D = 2 [ A x ( B y − C y ) + B x ( C y − A y ) + C x ( A y − B y ) ] . {\displaystyle D=2\left} A_{x}(B_{y}-C_{y})+B_{x}(C_{y}-A_{y})+C_{x}(A_{y}-B_{y}\right]]\,} 일반성의 손실 없이, 이것 은 정점 A = A A = Ax ′,Ay = 0 , ). 표시 스타일 A-A A'_{x}) A'_{y}=(0,0). 이정점 ' = B A ({displaystyle B-A} 및 = C A displaystyle C-A}) 정점 A' 에서 이 정점까지의 벡터를 나타냅니다. 이 사소한 변환이 모든 삼각형 중심 U = U ′, Y ▁) ){displaystyle U' _{ 삼각형 △ A'B'C' '_{y}} 같습니다
U x ′ = 1 D ′ [ C y ′ ( B x ′ 2 + B y ′ 2 ) − B y ′ ( C x ′ 2 + C y ′ 2 ) ] , U y ′ = 1 D ′ [ B x ′ ( C x ′ 2 + C y ′ 2 ) − C x ′ ( B x ′ 2 + B y ′ 2 ) ] 스타일 표시({{aligned}) U'_{x}&=nbfrac{1}{D'}\left[C'_{y}({B'_{x})^{2}+{Y}^{2})-B'_{y}({C'_{x}}^{2})+{C'_{y}^{2}}\right,\[5] U'_{y}&=nbfrac{1}{D'}\left[B'_{x}}({C'_{x})^{2}+{C'_{x}}^{2}+{B'_{y}^{2}\right}\end{aligned}}} 와 함께
D ′ = 2 ( B x ′ C y ′ − B y ′ C x ′ ) . {\displaystyle D'=2(B'_{x}C'_{y}-B'_{y}C'_{x}).\,} 꼭짓점 A를 원점으로 변환하기 때문에, 원주율 r은 다음과 같이 계산될 수 있습니다.
r = ‖ U ′ ‖ = U x ′ 2 + U y ′ 2 {\displaystyle r=\U'\ =sksqrt {{U'_{x}}^{2}+{ U'_{y}}^{2}}} 그리고
U = U ′ + A 디스플레이 스타일 U=U'+ A} 삼선 좌표 원주 중심에 삼선 좌표 가 있습니다.
코스 α의 : 코스 β : 코스 γ {\displaystyle \cos \alpha :\cos \cos \calpha } 여기서 α, β, γ 는 삼각형의 각입니다.
변의 길이 a, b, c 의 관점에서, 삼선은[3]
a ( b 2 + c 2 − a 2 ) : b ( c 2 + a 2 − b 2 ) : c ( a 2 + b 2 − c 2 ) . {\displaystyle a\left(b^{2}+c^{2}-a^{2}\right):b\left(c^{2}+a^{2}-b^{2}\right):c\left(a^{2}+b^{2}-c^{2}\right)}. 무게중심 좌표 원주 중심에는 무게 중심 [4]
a 2 ( b 2 + c 2 − a 2 ) : b 2 ( c 2 + a 2 − b 2 ) : c 2 ( a 2 + b 2 − c 2 ) , {\displaystyle a^{2}\left(b^{2}+c^{2}-a^{2}\right): \;b^{2}\left(c^{2}+a^{2}-b^{2}\right): \;c^{2}\left(a^{2}+b^{2}-c^{2}\right),\,} 여기 서 a, b, care 에지 길이 CA ,AB
삼각형의 각도 α, β, γ 에 대하여, 원주 중심의[3]
죄악 2 α의 : 죄악 2 β : 죄악 2 γ . displaystyle \sin 2\alpha :\sin 2\context :\sin 2\contexts} 원주 중심 벡터 어떤 점의 데카르트 좌표는 꼭짓점의 좌표의 가중 평균이고, 가중치는 점의 무게중심 좌표를 합으로 정규화하여 다음과 같이 쓸 수 있습니다.
U = a 2 ( b 2 + c 2 − a 2 ) A + b 2 ( c 2 + a 2 − b 2 ) B + c 2 ( a 2 + b 2 − c 2 ) C a 2 ( b 2 + c 2 − a 2 ) + b 2 ( c 2 + a 2 − b 2 ) + c 2 ( a 2 + b 2 − c 2 ) . {\displaystyle U=displayfrac {a^{2}\left(b^{2}+c^{2}-a^{2}\right) A+b^{2}\left(c^{2}+a^{2}-b^{2}\right) B+c^{2}\left(a^{2}+b^{2}-c^{2}\right) C}{a^{2}\left(b^{2}+c^{2}-a^{2}\right)+b^{2}\left(c^{2}+a^{2}-b^{2}\right)+c^{2}\left(a^{2}+b^{2}-c^{2}\right)}}. 여기 서 U는 원주 중심의 벡터 이고 A, B, C 는 꼭짓점 벡터입니다.여기서 제수는 16S와 같고 , 여기 서 S는 삼각형의 면적입니다. 전술한 바와 같이
a = A − C , b = B − C . 표시({style\mathbf {a} &=\mathbf {A} -\mathbf {C},\\mathbf {b} &=\mathbf {B} -\mathbf {C} .\end{aligned}) 교차곱과 점선곱의 데카르트 좌표 유클리드 공간 에서, 주어진 세 개의 비공선점 P 1 , P2 3 공간 벡터 로 표현하기 위해 데카르트 좌표 를 사용하면 점 곱과 교차 곱을 사용하여 원의 반지름과 중심을 계산할 수 있습니다.
P 1 = [ x 1 y 1 z 1 ] , P 2 = [ x 2 y 2 z 2 ] , P 3 = [ x 3 y 3 z 3 ] \displaystyle \mathrm {P_{1} ={bmatrix}x_{1}\y_{1}\z_{1}\end{bmatrix},\mathrm{P_{2}} ={bmatrix}x_{2}\z_{2}\matrix{P_3} ={bmatrix} }\\y_{3}\z_{3}\end{bmatrix}} 그러면 원의 반지름은 다음과 같이 주어집니다.
r = P 1 − P 2 P 2 − P 3 P 3 − P 1 2 ( P 1 − P 2 ) × ( P 2 − P 3 ) {\displaystyle \mathrm {r} = newfrac \left P_{1}-P_{2}\right \left P_{3}-P_{1}-P_{2}\right}{2}\left(P_{2}-P_{3}\right)\times \left(P_{2}-{3})\right}\right}\right} 원의 중심은 선형 조합 에 의해 주어집니다.
P c = α의 P 1 + β P 2 + γ P 3 {\displaystyle \mathrm {P_{c}} =\alpha \,P_{1}+\beta \,P_{2}+\감마 \,P_{3}} 어디에
α의 = P 2 − P 3 2 ( P 1 − P 2 ) ⋅ ( P 1 − P 3 ) 2 ( P 1 − P 2 ) × ( P 2 − P 3 ) 2 β = P 1 − P 3 2 ( P 2 − P 1 ) ⋅ ( P 2 − P 3 ) 2 ( P 1 − P 2 ) × ( P 2 − P 3 ) 2 γ = P 1 − P 2 2 ( P 3 − P 1 ) ⋅ ( P 3 − P 2 ) 2 ( P 1 − P 2 ) × ( P 2 − P 3 ) 2 표시({style{aligned}\alpha = lightfrac{leftP_{2}-P_{3}\right)\cdot \left(P_{1}-P_{3}\right)\left(P_{1}-P_{2}\right)\left(P_{2}-{2}\right)\left(P_{2}\right)\light(P_{\light)\light)\light(P_{\light(P_{\light)\left( (P_{2}-P_{3}\right)\right ^{2}}\\\cdot ^{2}\left(P_{3}-P_{1}\right)\cdot \left(P_{3}-P_{2}\right){2}\left(P_{1}-{2}\right)\times\left(\left)\light_{P_2}\left(\left(\times\left)\left(\times\left)\ 삼각형을 기준으로 한 위치 원주 중심의 위치는 삼각형의 유형에 따라 달라집니다.
예각 삼각형(직각보다 작은 모든 각도)의 경우 원주 중심은 항상 삼각형 안에 있습니다. 직각 삼각형의 경우 원주 중심은 항상 빗변 의 중간 지점에 있습니다. 이것은 탈레스 정리 의 한 형태입니다. 둔각 삼각형(직각보다 한 각도가 큰 삼각형)의 경우 원주 중심은 항상 삼각형 바깥쪽에 있습니다. 예각 삼각형의 원주 중심은 삼각형 안에 있습니다.
직각 삼각형의 원주 중심은 빗변의 중간 지점에 있습니다.
둔각 삼각형의 원주 중심은 삼각형의 바깥쪽에 있습니다.
이러한 위치 특징은 원주 중심에 대해 위에 주어진 삼선 또는 무게 중심 좌표를 고려하여 볼 수 있습니다. 세 좌표 모두 내부 점에 대해 양수이고, 적어도 하나의 좌표는 외부 점에 대해 음수이며, 하나의 좌표는 0이고 삼각형의 한 변에 있는 비직각 점에 대해서는 양수입니다.
각도
외접원이 삼각형의 변과 이루는 각도는 변이 서로 만나는 각도와 일치합니다. 반대쪽 각도 α는 원과 두 번 만난다: 한 번은 양쪽 끝에서, 각 경우 에는 각도 α에서. (다른 두 각도와 유사하게) 이는 접선과 코드 사이의 각도가 대체 세그먼트의 각도와 같다는 대체 세그먼트 정리 때문입니다.
삼각형이 원의 중심을 맞춥니다. 이 섹션에서 정점 각도는 A, B, C로 표시 되며 모든 좌표는 3선 좌표 입니다.
스타이너 점: 원주와 스타이너 타원의 교차점의 정점이 아닙니다. b c b 2 − c 2 : c a c 2 − a 2 : a b a 2 − b 2 {\style {bc}{b^{2}-c^{2}}:{\frac {ca}{c^{2}-a^{2}}:{\frac {ab}{a^{2}-b^{2}}} 표시 (중심점 = 중심(ABC) 이 있는 스타이너 타원 은 A, B, C를 통과 하는 최소 면적의 타원입니다. 이 타원에 대한 방정식 1 1 x 1 cz = 0 displaystyle tfrac {1}{ax}}+{\tfrac {1}{cz 0 초 ( A + ω ) : 초 ( B + ω ) : 초 ( C + ω ) {\displaystyle \sec(A+\omega):\sec(B+\omega):\sec(C+\omega)} csc ( B − C ) : csc ( C − A ) : csc ( A − B ) . {\displaystyle \csc(B-C):\csc(C-A):\csc(A-B)} 기타 속성 원주 지름이라고 하며 원주 반경의 두 배와 동일한 원주의 지름 은 삼각형의 모든 변의 길이를 반대 각도 의 사인으로 나눈 값으로 계산할 수 있습니다.
지름 = a 죄악 A = b 죄악 B = c 죄악 C . display{style{text{c}}=tftfrac{a}{\sin A}=tftfrac{b}{\sin B}=tftfrac{c}{\sin C}} 사인의 법칙 의 결과로, 어느 쪽과 반대의 각도를 취하느냐는 중요하지 않습니다. 결과는 같을 것입니다.
원의 지름은 다음과 같이 표현할 수 있습니다.
지름 = a b c 2 ⋅ 지역 = A B B C C A 2 Δ A B C = a b c 2 s ( s − a ) ( s − b ) ( s − c ) = 2 a b c ( a + b + c ) ( − a + b + c ) ( a − b + c ) ( a + b − c ) 표시{style{aligned}{\text{cdot{text{area}}&{}=cdot{text{area}}=cdfrac{ABCA}{2 \Delta ABC }}\[5pt]& {}=nbfrac {bflac}{2pvsqrt {s(s-a)(s-b)(s-c)}}}\[5pt]& {}=sqfrac {2px}{\sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c) }}}\end{aligned}}} 여기 서 a, b, c 는 삼각형의 변의 길이 = b c {\ displaystyle tftfrac {a + c}{2 반지름 위의 s s b s c displaystyle \scriptstyle sqrt {s(s-a)(s-b)(s-c)} 공식 에 [5] 의한 삼각형의 면적입니다. 원의[6]
지름 = 2 ⋅ 지역 죄악 A 죄악 B 죄악 C . display{style{text{text}}=sksqrt{frac{2\cdot{text{area}}{\sin A\sin B\sin C}}} 삼각형의 9점 원의 지름은 원의 절반입니다.
주어진 삼각형에서 원주 중심은 항상 중심 및 직교 중심과 일직선입니다. 이들을 모두 통과하는 선을 오일러 선이 라고 합니다.
원주 중심의 등교 공역 은 직교 중심입니다.
세 점의 유용한 최소 경계 원은 원주(세 점이 최소 경계 원에 있는 경우) 또는 삼각형의 가장 긴 변의 두 점(두 점이 원의 직경을 정의하는 경우)으로 정의됩니다. 최소 경계 원과 원을 혼동하는 것이 일반적입니다.
세 개의 공선 점의 원은 세 개의 점이 놓여 있는 선이며, 종종 무한 반지름의 원 이라고 합니다. 거의 동일한 점들은 종종 원주의 계산에서 수치적 불안정성 을 초래합니다.
삼각형의 원은 점 집합 의 들라우네 삼각 측량과 밀접한 관계가 있습니다.
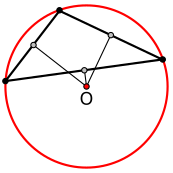
기하학에서 오일러의 정리 에 따르면, 원주 중심 O와 인센티브 I 사이의 거리는
O I ¯ = R ( R − 2 r ) , {\style {OI}}표시=svsqrt {R(R-2r)},} 여기 서 r은 원 반지름이고 R 은 원 반지름입니다. 따라서 원주 반지름은 인 반지름의 최소 두 배입니다( 오일러 의 삼각형 부등식).[7] [8]
O와 직교 중심 H 사이 의[9] [10]
O H ¯ = R 2 − 8 R 2 코스 A 코스 B 코스 C = 9 R 2 − ( a 2 + b 2 + c 2 ) . {\style{overline{OH}}=nbsqrt {R^{2}-8R^{2}\cos A\cos B\cos C}=nbsqrt {9R^{2}-(a^{2}+b^{2}+c^{2}}}}}을(를) 표시합니다. 중심 G와 9점 중심 N에 대하여 우리는 다음과 같은
I G ¯ < I O ¯ , 2 I N ¯ < I O ¯ , O I ¯ 2 = 2 R ⋅ I N ¯ . {\style}{\overline} IG}&<{\overline{ IO},\2{\overline{ IN}&<{\overline{ IO},\\{\overline{OI}}^{2}&=2R\cdot{overline{IN}}. \end{aligned}}} 변 a, b, c 를[11]
r R = a b c 2 ( a + b + c ) . {\displaystyle rR=displayfrac {discovery}{2(a+b+c) }}.} 원주율 R, 변 a, b , c, 그리고a 중위수 mb , mc , m을 사용하면, 우리는[12]
3 3 R ≥ a + b + c 9 R 2 ≥ a 2 + b 2 + c 2 27 4 R 2 ≥ m a 2 + m b 2 + m c 2 . 디스플레이({stylebegin{aligned}3{\sqrt{3}}R&\geq a+b+c\[5pt]9 R^{2}&\geq a^{2}+b^{2}+c^{2} }\\[5pt]{\frac{27}{4}}R^{2}&\geq m_{a}^{2}+m_{b}^{2}+m_{c}^{2}. \end{aligned}}} 만약 중앙값 m, 고도 h, 내부 이등분선 이 모두 삼각형의 동일한 꼭짓점에서 반경 R로 나온다면[13]
4 R 2 h 2 ( t 2 − h 2 ) = t 4 ( m 2 − h 2 ) . \"표시 스타일 4R^{2}h^{2}(t^{2}-h^{2})=t^{4}(m^{2}-h^{2})}. 카르노의 정리 에 따르면 원주 중심에서 세 변까지의 거리의 합은 원주 와 반지름의 합과 같습니다.여기서 세그먼트 길이는 세그먼트가 완전히 삼각형 외부에 있는 경우에만 음수로 간주됩니다.
삼각형이 원과 원 으로 두 개의 특정 원을 가지고 있다면, 원 위의 점을 꼭짓점으로 하여 같은 원과 원을 가진 다른 삼각형이 무한히 존재합니다. (이 폰세레 포리즘 의 경우 n = 3 ) 이러한 삼각형이 존재하기에 필요하고 충분한 조건은 위의 동일 OI ¯ = R - 2 overline {OI sqrt {R(R-2r)}
순환 다각형 순환 사변형 같은 원 위에 놓여 있는 점들의 집합을 원환 원환 모든 삼각형은 원환형이지만, 변이 3개 이상인 다각형은 일반적으로 그렇지 않습니다.
순환 다각형, 특히 4면 순환 사변형 은 다양한 특수한 특성을 가집니다. 특히, 순환 사각형의 반대각은 보조각 입니다(최대 180° 또는 µ 라디안 추가).
참고 항목 레퍼런스 ^ Whitworth, William Allen (1866). Trilinear Coordinates and Other Methods of Modern Analytical Geometry of Two Dimensions 199 . ^ a b Kimberling, Clark. "Part I: Introduction and Centers X(1) – X(1000)" . Encyclopedia of Triangle Centers . ^ Weisstein, Eric W. "Barycentric Coordinates" . MathWorld ^ Coxeter, H.S.M. (1969). "Chapter 1". Introduction to geometry 12–13 . ISBN 0-471-50458-0 ^ Dörrie, Heinrich (1965). 100 Great Problems of Elementary Mathematics . Dover. p. 379. ^ Nelson, Roger, "말 없는 증명을 통한 오일러의 삼각 부등식 ", Mathematics Magazine 81 (1), 2008년 2월, 58-61 ^ Svrtan, Dragutin; Veljan, Darko (2012). "Non-Euclidean versions of some classical triangle inequalities" . Forum Geometricorum . 12 : 197–209. ^ Gras, Marie-Nicole (2014). "Distances between the circumcenter of the extouch triangle and the classical centers" . Forum Geometricorum . 14 : 51–61. ^ Smith, G. C.; Leversha, Gerry (November 2007). "Euler and triangle geometry". The Mathematical Gazette 91 (522): 436–452. doi :10.1017/S0025557200182087 . JSTOR 40378417 . S2CID 125341434 . ^ Johnson, Roger A. (1929). Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle . Houghton Mifflin Co. p. 189, #298(d). hdl :2027/wu.89043163211 . 의해 고급 유클리드 기하학으로 재출판, 1960년 및 2007년.^ Posamentier, Alfred S.; Lehmann, Ingmar (2012). The Secrets of Triangles ^ Altshiller Court, Nathan (1952). College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle (2nd ed.). Barnes & Noble. p. 122, #96.
외부 링크 수학의 세계 상호적인 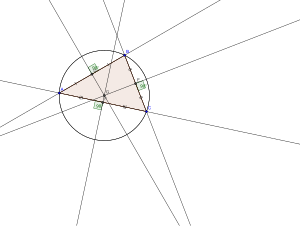



 궤적입니다.
궤적입니다.
 모두
모두 

![{\displaystyle {\begin{aligned}S_{x}&={\frac {1}{2}}\det {\begin{bmatrix}|\mathbf {A} |^{2}&A_{y}&1\\|\mathbf {B} |^{2}&B_{y}&1\\|\mathbf {C} |^{2}&C_{y}&1\end{bmatrix}},\\[5pt]S_{y}&={\frac {1}{2}}\det {\begin{bmatrix}A_{x}&|\mathbf {A} |^{2}&1\\B_{x}&|\mathbf {B} |^{2}&1\\C_{x}&|\mathbf {C} |^{2}&1\end{bmatrix}},\\[5pt]a&=\det {\begin{bmatrix}A_{x}&A_{y}&1\\B_{x}&B_{y}&1\\C_{x}&C_{y}&1\end{bmatrix}},\\[5pt]b&=\det {\begin{bmatrix}A_{x}&A_{y}&|\mathbf {A} |^{2}\\B_{x}&B_{y}&|\mathbf {B} |^{2}\\C_{x}&C_{y}&|\mathbf {C} |^{2}\end{bmatrix}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1649c42b7532a101a98ee8d0eb5f18f72a4922a1)


![{\displaystyle \mathrm {R} (s)=\mathrm {P_{c}} +\cos \left({\frac {\mathrm {s} }{\mathrm {r} }}\right)(P_{0}-P_{c})+\sin \left({\frac {\mathrm {s} }{\mathrm {r} }}\right)\left[{\widehat {n}}\times (P_{0}-P_{c})\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a70aa6cf6f613352caa88916c82a86f03bbc8b4)






![{\displaystyle {\begin{aligned}U_{x}&={\frac {1}{D}}\left[(A_{x}^{2}+A_{y}^{2})(B_{y}-C_{y})+(B_{x}^{2}+B_{y}^{2})(C_{y}-A_{y})+(C_{x}^{2}+C_{y}^{2})(A_{y}-B_{y})\right]\\[5pt]U_{y}&={\frac {1}{D}}\left[(A_{x}^{2}+A_{y}^{2})(C_{x}-B_{x})+(B_{x}^{2}+B_{y}^{2})(A_{x}-C_{x})+(C_{x}^{2}+C_{y}^{2})(B_{x}-A_{x})\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79248a1cfbeff74ea283e3c6c07a289fe188fb4d)
![D=2\left[A_{x}(B_{y}-C_{y})+B_{x}(C_{y}-A_{y})+C_{x}(A_{y}-B_{y})\right].\,](https://wikimedia.org/api/rest_v1/media/math/render/svg/34c6178eff86289b6ec6f7dd49c95d675180f944)


 좌표는
좌표는  다음과
다음과 ![{\displaystyle {\begin{aligned}U'_{x}&={\frac {1}{D'}}\left[C'_{y}({B'_{x}}^{2}+{B'_{y}}^{2})-B'_{y}({C'_{x}}^{2}+{C'_{y}}^{2})\right],\\[5pt]U'_{y}&={\frac {1}{D'}}\left[B'_{x}({C'_{x}}^{2}+{C'_{y}}^{2})-C'_{x}({B'_{x}}^{2}+{B'_{y}}^{2})\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae86c30103fce308b05684855b6c7241218358ad)





















![{\displaystyle {\begin{aligned}{\text{diameter}}&{}={\frac {abc}{2\cdot {\text{area}}}}={\frac {|AB||BC||CA|}{2|\Delta ABC|}}\\[5pt]&{}={\frac {abc}{2{\sqrt {s(s-a)(s-b)(s-c)}}}}\\[5pt]&{}={\frac {2abc}{\sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47584c5d8064a85b773192bd5c30ff505b51ac6a)
 .위의
.위의 헤론
헤론




![{\displaystyle {\begin{aligned}3{\sqrt {3}}R&\geq a+b+c\\[5pt]9R^{2}&\geq a^{2}+b^{2}+c^{2}\\[5pt]{\frac {27}{4}}R^{2}&\geq m_{a}^{2}+m_{b}^{2}+m_{c}^{2}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/790d28d5425086fee0f7465ed10d65aab26b5586)



