등각 다각형

등각 다각형 예제
직접	간접적	스큐
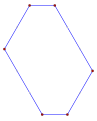
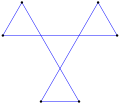
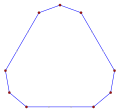
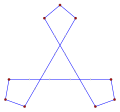
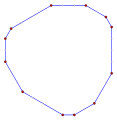
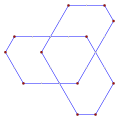
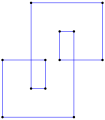
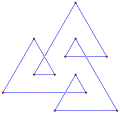
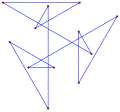
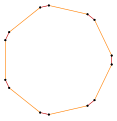
직사각형, <4>는 볼록한 직사각형 다각형으로, 내부 각 4개의 90°를 포함하고 있다.	오목한 간접 등각형 다각형, <6-2>는 이 육각형처럼 시계 반대방향으로, 이 테트로미노처럼 좌회전 5회, 우회전 1회를 가진다.	스큐 폴리곤은 입방체에서 빨간색과 파란색 가장자리가 번갈아 나타나는 이 스큐 팔각형처럼 평면에서 동일한 각도를 가진다.
직접	간접적	카운터-변형
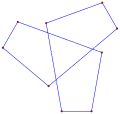
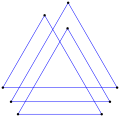
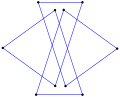
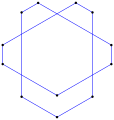
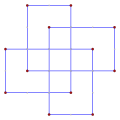
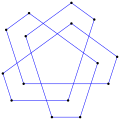
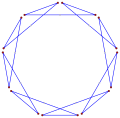
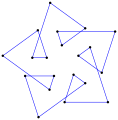
다중 회전 등각 다각형은 이 팔각형 <8/2>처럼 직각일 수 있는데, 8 90° 회전하여 총 720°이다.	오목한 간접 등각형 다각형, <5-2>, 반시계방향으로 좌회전 4회, 우회전 1회. (- 1.2.4.3.2)_60°	좌회전 3회, 우회전 3회, 합계 0°의 간접 등각 육각형 육각 <6-6>_90°이다.

유클리드 기하학에서 등각형 다각형은 정점 각도가 같은 다각형이다. 옆면의 길이도 같다면(즉, 등각형이라면) 일반 다각형이다. 등각 폴리곤은 두 개의 가장자리 길이를 번갈아 갖는 등각형 폴리곤이다.

명확성을 위해 평면 등각형 다각형은 직접 또는 간접이라고 할 수 있다. 직사각형 다각형은 평면에서 동일한 방향으로 회전하는 모든 각도를 가지며 다중 회전을 포함할 수 있다. 볼록한 등각형 다각형은 항상 직접적이다. 간접 등각형 다각형은 어떤 조합에서든 오른쪽 또는 왼쪽으로 회전하는 각도를 포함할 수 있다. 등각형 다각형은 등각형일 수 있지만 평면형이 아니기 때문에 직접이라고 볼 수 없다.

spirolateral n은_θ 시작에 복귀할 때까지 정수 가장자리 길이가 반복되는 일련의 n의 등각형 다각형의 특별한 경우로, 정점 내부 각도가 θ이다.

건설

이 볼록한 직사각형 육각형인 <6>는 60°의 각도를 가진 6개의 선으로 경계를 이룬다. 각 선은 그 방향에 수직으로 이동할 수 있다.	이 오목한 간접 등각 육각형 육각형인 <6-2>도 각각 90° 각도를 가진 6개의 선으로 경계를 이루며, 각 선은 독립적으로 움직이며, 정점을 새로운 교차점으로 이동시킨다.

등각형 다각형은 가장자리가 무한선으로 확장되는 일반 다각형 또는 일반 별 다각형으로 구성할 수 있다. 각 가장자리는 선의 방향에 수직으로 독립적으로 이동할 수 있다. 꼭지점은 인접한 선 쌍 사이의 교차점을 나타낸다. 이동한 각 선은 가장자리 길이와 두 가장자리 길이를 조정한다.^[1] 가장자리가 0 길이로 줄어들면 폴리곤이 퇴화되거나 음 길이로 줄어들면 내각과 외각이 역전된다.

내부 각도가 θ°인 편평한 측면 직각 다각형의 경우, 이동 대체 에지는 모든 정점을 180 θ°의 보조 각도로 반전시킬 수 있다. 홀수 면 직사각형 다각형은 부분적으로만 반전될 수 있으며, 보조 각도가 혼합되어 있다.

모든 등각형 다각형은 이 구조에 의해 비율로 조정될 수 있으며, 여전히 등각형 상태를 유지할 수 있다.

등각 다각형 정리

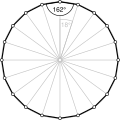
볼록 등각 p-곤의 경우, 각 내부 각도는 180(2/p)°이다. 이것이 등각형 다각형 정리다.

직사각형 모양의 p/q 별 폴리곤, 밀도 q의 경우, 각 내부 각도는 180(-1-2q/p)°이고, 1<2q<p. w=gcd(p,q)>1의 경우, 이것은 w-wound (p/w)/(q/w)별 다각형을 나타내며, 일반 케이스에 대해 퇴보한다.

오목한 간접 등각형(p_r+p_l)-곤은 우측_r 방향 정점과 좌측_l 방향 정점이 있으며, 순서에 관계없이 내부 각도가 180(-1-2/p_r_l)°이다. p_r 우회전 정점과 p_l 좌회전 정점과 q 총 회전을 갖는 간접 항성 등각형(p_r+p_l)-곤은 순서에 관계없이 180(-2q/p-p_r_l )°의 내부 각도를 갖는다. 좌우 턴 수가 같은 등각형 다각형은 총 턴이 0이며, 각도에 제약이 없다.

표기법

모든 직각 p-곤에는 p 정점을 포함하는 일반 폴리곤 {p} 및 일반 별 폴리곤 {p/q}과 같은 표기법 <p> 또는 <p/q>가 주어질 수 있다.

볼록 등각 p-곤 <p>는 내부 각도가 180(1-2/p)°이고, 직각 항성 등각 폴리곤은 내부 각도가 180(1-2q/p)°이다.

오목한 간접 등각 p-곤은 c 역회전 정점과 함께 표기법 <p-2c>를 부여할 수 있다. 예를 들어, <6-2>는 차이의 내부 각도가 90°인 육각, <4>, 1개의 카운터 변환 정점이다. 다항 간접 등변형 p-곤은 c 카운터 턴 정점과 q 총 턴을 갖는 표기법 </>^p-2c_q를 부여할 수 있다. 등각형 다각형 <p-p>는 내부 각도가 정의되지 않은 p-곤이지만, 명시적으로 <p-p>_θ로 표현할 수 있다.

기타 속성

Viviani의 정리는 등각형 다각형에 대한 것이다.^[2]

내부 지점에서 등각 다각형의 측면까지의 거리의 합은 점의 위치에 따라 달라지지 않으며, 그 다각형의 불변성이다.

주기적인 다각형은 만약 다른 면이 같다면 등각형이고 (즉, 면 1, 3, 5, ...가 같고 면 2, 4, ...가 같을 경우에만 등각형이다. 따라서 n이 홀수인 경우에는 주기적인 다각형이 정규적인 경우에만 등각형이다.^[3]

prime p의 경우, 모든 정수측 등각 p-곤은 규칙적이다. 더욱이 모든 정수측 등각형 p-곤은^k p-폴드 회전 대칭을 가진다.^[4]

An ordered set of side lengths $(a_{1},\dots ,a_{n})$ gives rise to an equiangular n-gon if and only if either of two equivalent conditions holds for the polynomial ${\displaystyle a_{1}+a_{2$ $}x+\cdots +a_{n-1}x^{n-2}+a_{n}x^{n-1}:}$ it equals zero at the complex value $e^{2\pi i/n};$ it is divisible by ${\displaystyle x^{2}-2x\cos(2\pi /n)+1.$ $}$ ^[5]

측면으로 직각형 다각형

직등각형 다각형은 정규, 등각형 또는 하부 대칭일 수 있다. <p/q>의 예시는 p별로, 밀도 q별로 세분화되어 있다.

등각 삼각형

등각 삼각형은 볼록하고 내부 각도가 60°여야 한다. 정삼각형이며 정삼각형인 <3>={3}이다. 자유의 유일한 정도는 가장자리 길이다.

정규₆, {3}, r

등각형 사방측정감시

2×3 정사각형 배열로^[6] 절개된 직사각형

직사각형 4각형 측정기들은 내부 각도가 90°이다. 유일한 등각형 사변측정감시로는 직사각형, <4>, 정사각형, {4}이(가) 있다.

정수의 측면 길이가 있는 등각형 사각형은 단위 정사각형으로 타일링할 수 있다.^[6]

정규₈, {4}, r
측방향₄ 2_90°, p

등각 펜타곤

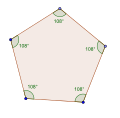
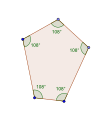
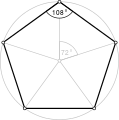
직각 펜타곤, <5>와 <5/2>는 각각 108°와 36°의 내부 각도를 가지고 있다.

등각 오각형 오각형에서 108° 내부 각도, <5

등각형 펜타곤은 규칙적일 수도 있고, 양쪽 대칭이 있을 수도 있고, 대칭이 없을 수도 있다.

정규₁₀, r
양자₂ 대칭, i
대칭 없음, a₁

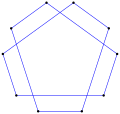
등각 펜타그램에서 36° 내부 각도, <5/2>

정규₁₀ 펜타그램, r
불규칙₂, d

등각형 육각형

가장자리 길이 비율이 1:2인 정삼각형이고 정삼각형이 있는 정삼각형입니다.^[6] 여긴 측두엽 2번이야_120°

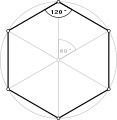
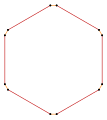
직각 육각형 육각형인 <6>와 <6/2>는 각각 120°와 60°의 내부 각도를 가진다.

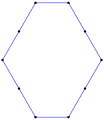
등각 육각형 육각의 120° 내부 각도, <6>

정수의 측면 길이가 있는 등각형 육각형은 단위 등각 삼각형으로 타일링할 수 있다.^[6]

정규₁₂, {6}, r
측방향₆(1,2),_120° p
측방향₂(1…3),_120° g
측방향(1,2,2),_120° i₄
측방향₂(1,2,2,2,1,3)_120°

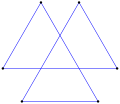
등각형 이중 삼각형의 60° 내부 각도, <6/2>

정규₆, 퇴보, r
측방향₆(1.3), _60°p
측방향₆(1,2),_60° p
측방향₆(2,_60°3)
측방향₂(1,2,3,4,3,2),_60° p

등각 헵타곤

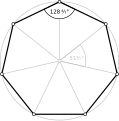
직각 헵타곤, <7>, <7/2>, <7/3>은 각각 128 4/7°, 77 1/7°, 25 5/7°의 내부 각도를 가진다.

등각 헵타곤의 128.57° 내부 각도, <7>

정규₁₄, {7}, r
불규칙₂, i

77.14° 등각 헵타그램의 내부 각도, <7/2>

정규₁₄, r
불규칙₂, i

등각 헵타그램의 25.71° 내부 각도, <7/3>

정규₁₄, r
불규칙₂, i

등각형 옥타곤

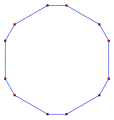
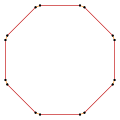
직각형 옥타곤, <8>, <8/2>, <8/3>은 각각 내부 각도가 135도, 90도, 45도이다.

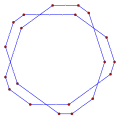
등각 8각형에서 135° 내부 각도, <8>

정규₁₆, r
측방향₈(1,2),_135° p
측방향(1…4),_135° g₂
균일하지 않은 잘림 사각형, p₂

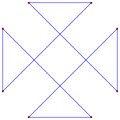
등각형 이중 사각형에서 90° 내부 각도, <8/2>

규칙적으로₈ 퇴화, r
측방향₂(1,2,2,3,3,2,2,1,), _90°d
측방향₂(2,1,3,2,2,3,1,2,2) _90°d

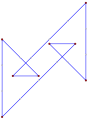
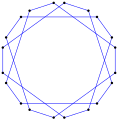
등각형 옥타그램에서 45° 내부 각도, <8/3>

정규₁₆, r
등각₈, p
등각₈, p
측방향₈(Spirolateral), (1,2),_45° p
등각₈, p
측방향(1…4),_45° g₂

등각형 엔네아곤

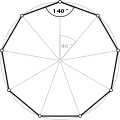
직등각형 enneagons, <9>, <9/2>, <9/3>, <9/4>는 각각 140°, 100°, 60°, 20°의 내부 각도를 가진다.

등각형 에네아곤 <9>에서 140° 내부 각도

정규₁₈, r
측방향₆(_140°1,1,3)

등각형 에네그램에서 100° 내부 각도, <9/2>

정규₉ {9/2}, p
측방향(1,1,5),_100° i₆
측방향_100°₃ 3, g

등각 3각 삼각형에서 60° 내부 각도, <9/3>

정규₆, 퇴보, r
불규칙₁, a
불규칙₁, a
불규칙₁, a

등각형 에네그램에서 20° 내부 각도, <9/4>

정규₁₈ {9/4}, r
측방향_20°₃ 3, g
불규칙₂, i

등각형 데카곤

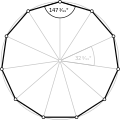
직각형 디카곤, <10>, <10/2>, <10/3>, <10/4>는 각각 144°, 108°, 72°, 36°의 내부 각도를 가진다.

등각형 데카곤 <10>에서 144° 내부 각도

정규₂₀, r
측방향₁₀(1,2),_144° p
측방향₂(1…5) _144°g

등각형 이중 사각 펜타곤 <10/2>에서 108° 내부 각도

규칙적이고 퇴보적인
측방향₁₀(1,2),_108° p
불규칙₂, p

등각 디카그램 <10/3>에서 72° 내부 각도

정규₂₀ {10/3}, r
등각₁₀, p
측방향₁₀(1,2),_72° p
불규칙₄, i
측방향₂(1…5) _72°g

등각형 이중 사각 펜타그램 <10/4>에서 36° 내부 각도

정규₁₀, 퇴보, r
측방향₁₀(1,2),_36° p
등각₁₀, p
등각₁₀, p
불규칙₂, p
불규칙₂, p
불규칙₂, p

등각형 헨데카곤스

직각 헨데카곤, <11>, <11/2>, <11/3>, <11/4>, <11/5>는 각각 3/117°, 114 6/11°, 81 9/11°, 49 1/11°, 16 4/11°의 내부 각도를 가지고 있다.

등각형 hendecagon에서 147° 내부 각도, <11>

정규₂₂, {11}, r

등각형 헨데카그램에서 114° 내부 각도, <11/2>

정규₂₂ {11/2}, r

등각형 헨데카그램에서 81° 내부 각도, <11/3>

정규₂₂ {11/3}, r

등각형 헨데카그램에서 49° 내부 각도, <11/4>

정규₂₂ {11/4}, r

등각형 헨데카그램에서 16° 내부 각도, <11/5>

정규₂₂ {11/5}, r

등각형 도데카곤

직각 도데카곤, <12>, <12/2>, <12/3>, <12/4>, <12/5>는 각각 150°, 120°, 90°, 60°, 30°의 내부 각도를 가지고 있다.

등각 도데카곤으로부터 150° 내부 각도, <12>

가장자리 길이가 정수인 볼록 용액은 패턴 블록, 정사각형, 정삼각형 및 30°옴비로 타일링할 수 있다.^[6]

정규₂₄, {12}, r
등각₁₂, p
측방향₁₂(1,2),_150° p
측방향₄(1…3),_150° g
측방향(1…4),_150° g₃
측방향₂(1…6) _150°g

등각형 2중 6각형에서 120° 내부 각도, <12/2>

규칙적으로₁₂ 퇴화, r
측방향₃, (1…4),_120° g
불규칙₂, d
불규칙₂, d

등각 3각 정사각형으로부터 90° 내부 각도, <12/3>

정규₈, 퇴보, r
측방향₂(1…3),_90° g
측방향₄(2…4) _90°g
측방향₈(_90°1,1,3)
측방향(1,2,2),_90° i₈
측방향₂(1…6) _90°g
불규칙₁, a

등각 4중 삼각형에서 60° 내부 각도, <12/4>

정규₆, 퇴보, r
측방향₆(1,3,5,1)_60°
측방향(1…4),_60° g₃
불규칙₁, a

등각 도데카그램에서 30° 내부 각도, <12/5>

정규₂₄ {12/5}, r
등각₁₂, p
측방향₁₂(1,2),_30° p
측방향₄(1…3),_30° g
측방향(1…4),_30° g₃
측방향₂(1…6) _30°g

등각 테트라데카곤스

직사각형 테트라데카곤, <14>, <14/2>, <14/3>, <14/4>, <14/6>, <14/5>는 각각 154 2/7°, 128 4/7°, 102 6/7°, 77 1/7°, 51/7°, 25/7°의 내부 각도를 가진다.

154.28° 등각 테트라데카곤으로부터 내부 각도, <14>

정규₂₈ {14}, r
등각₁₄, t{7}, p

등각형 이중 헵타곤으로부터 128.57° 내부 각도, <14/2>

규칙적으로₁₄ 퇴화, r
등각₁₄, t{7/2}, p
스피롤론트_128.57° 2

102.85° 등각형 테트라데카그램에서 내부 각도 <14/3>

정규₂₈ {14/3}, r
등각₁₄ t{7/3}, p

77.14° 등각형 이중 헵타그램 <14/4>에서 내부 각도

규칙적으로₁₄ 퇴화, r
등각₁₄, p
등각₁₄, p
스피롤론트_77.14° 2

등각형 테트라데카그램에서 51.43° 내부 각도, <14/5>

정규₂₈ {14/5}, r
등각₁₄, p
등각₁₄, p

등각형 이중 헵타그램에서 25.71° 내부 각도, <14/6>

규칙적으로₁₄ 퇴화, r
등각₁₄, p
등각₁₄, p
등각₁₄, p
불규칙₂, d

등각 펜타데카곤

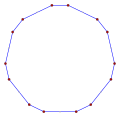
직각 펜타데카곤, <15>, <15/2>, <15/3>, <15/4>, <15/5>, <15/6>, <15/7>은 각각 156°, 132°, 108°, 84°, 60°, 12°의 내부 각도를 가지고 있다.

등각형 펜타데카곤으로부터 156° 내부 각도, <15>

정규₃₀, {15}, r

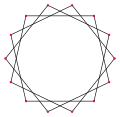
등각 펜타드카그램에서 132° 내부 각도, <15/2>

정규₃₀, {15/2}, r

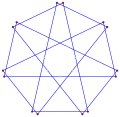
등각삼각형 오각형에서 108° 내부 각도, <15/3>

정규₁₀, 퇴보, r
spirolateral₅(1…3),_108° g

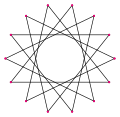
등각형 펜타데카그램에서 84° 내부 각도, <15/4>

정규₃₀, {15/4}, r

등각 5각 삼각형에서 60° 내부 각도, <15/5>

정규₆, 퇴보, r
불규칙₁, a

등각 3각 펜타그램에서 36° 내부 각도, <15/6>

정규₁₀, 퇴보, r
불규칙₁, a
측방향(1…4),_36° g₅

등각 펜타드카그램에서 12° 내부 각도, <15/7>

정규₃₀, {15/7}, r

등각형 육각형

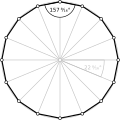
직사각형 육각형 육각각형, <16/2>, <16/3>, <16/4>, <16/5>, <16/6>, <16/7>은 각각 157.5도, 135도, 112.5도, 90도, 67.5도 45도, 22.5도 내부 각도를 가진다.

157.5° 등각 육각형 육각형으로부터 내부 각도, <16>

정규₃₂, {16}, r
등각₁₆, t{8}, p
측방향(1…4),_157.5° g₄

등각 2각 8각형에서 135° 내부 각도, <16/2>

정규₁₆, 퇴보, r
불규칙₁₆, p

등각 육각형 육각형에서 112.5° 내부 각도, <16/3>

정규₃₂, {16/3}, r

등각 4칸 정사각형으로부터 90° 내부 각도, <16/4>

정규₈, 퇴보, r
불규칙₁, a

등각 육각형 육각형에서 67.5° 내부 각도, <16/5>

정규₃₂, {16/5}, r

등각형 이중 삼각형 정규 옥타그램에서 45° 내부 각도, <16/6>

정규₁₆, 퇴보, r
spirolateral₈(1…3),_45° g

22.5° 등각 육각형 육각형에서 내부 각도, <16/7>

정규₃₂, {16/7}, r
등각₁₆, p

등각형 옥타데카곤

직각형 옥타데카곤, <18}, <18/3>, <18/4>, <18/5>, <18/6>, <18/6>, <18/7>, <18/8>은 각각 160도, 140도, 120도, 100도, 80도, 60도, 40도, 20도 내부 각도를 가진다.

등각형 옥타데카곤으로부터 160° 내부 각도, <18>

정규₃₆, {18}, r
등각₁₈, t{9}, p

등각형 이중음향 에네아곤으로부터 140° 내부 각도, <18/2>

규칙적이고 퇴보적인
측방향₁₈ 2_140°, p

등각 3각 육각 <18/3>의 120° 내부 각도

정규₁₈, 퇴보, r
불규칙적인₁

등각형 2중주 에네아그램 <18/4>의 내부 각도 100°

정규₁₈, 퇴보, r
측방향_100°₃ 2, g

등각형 옥타이드카그램 {18/5}의 내부 각도 80°

정규₃₆, {18/5}, r

등각 6각 삼각형의 60° 내부 각도 <18/6>

정규₆, 퇴보, r
불규칙적인₁

등각형 옥타이드카그램 <18/7>의 40° 내부 각도

정규₃₆, {18/7}, r
등각₁₈, p
등각₁₈, p
등각₁₈, p

등각형 이중선형 에너그램 <18/8>의 20° 내부 각도

정규₁₈, 퇴보, r
등각₁₈, p
등각₁₈, p
등각₁₈, p
등각₁₈, p
측방향₁₈ 2_20°, p
측방향₃ 6_20°, g

등각형 이코사곤

직각 이코사곤, <20>, <20/3>, <20/4>, <20/6>, <20/6>, <20/7>, <20/9>는 각각 162도, 126도, <20/6도>, <20/7도>, <20/9도, 90도, 72도, 54도, 18도 내부 각도를 가진다.

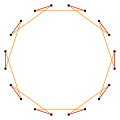
등각형 이코사곤으로부터 162° 내부 각도, <20>

정규₄₀, {20}, r
측방향₂₀(1.3), _162°p

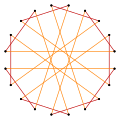
등각형 이중 삼각형 데카곤으로부터 144° 내부 각도, <20/2>

정규₂₀, 퇴보, r
측방향(1…4),_144° g₅

등각형 아이코사그램에서 126° 내부 각도, <20/3>

정규₄₀ {20/3}, p
측방향₂₀(1.3), _126°p

등각 4각 오각형 오각형에서 108° 내부 각도, <20/4>

규칙적으로₁₀ 퇴화, r
측방향(1…4),_108° g₅
불규칙₁, a

등각 5각 정사각형으로부터 90° 내부 각도, <20/5>

규칙적으로₈ 퇴화, r
측방향₄(1…5) _90°g
측방향₈(1,2,3,2,1),_90° i

등각형 이중 삼각형 데카그램에서 72° 내부 각도, <20/6>

규칙적으로₂₀ 퇴화, r
측방향₁₀(1,2),_72° p
측방향(1…4),_72° g₅

등각형 아이코사그램에서 54° 내부 각도, <20/7>

정규₄₀ {20/7}, r
등각₂₀, p
등각₂₀, p
등각₂₀, p

등각형 4중주 펜타그램에서 36° 내부 각도, <20/8>

규칙적으로₁₀ 퇴화, r
측방향(1…4),_36° g₅
불규칙적인₁

등각형 아이코사그램에서 18° 내부 각도, <20/9>

정규₄₀ {20/9}, r
등각₂₀, p
등각₂₀, p
등각₂₀, p
등각₂₀, p

참고 항목

스피롤론탈

참조

^ 마리우스 문테아누, 로라 문테아누, Rational Equiangular Polygons Applied Mathical, Vol.4 No.10, 2013년 10월
^ Elias Abboud "On Viviani's Organization and the Extensions" 페이지 2, 11
^ De Villiers, Michael, "Eqiangangular cyclic and quietronarycurrent polygons," Mathematical Gazette 95, 2011년 3월, 102-107년.
^ 맥클린, K. 로빈. "등각형 다각형을 위한 강력한 대수 도구," 2004년 11월, Mathematical Gazette 88, 513-514.
^ M. Bras-Amoros, M. Pujol: "Equiangular Polygons의 측면 길이"(코딩 이론가에게 보여짐), The American Mathematical Monthly, vol. 122, n. 5, 페이지 476–478, 2015년 5월. ISSN 0002-9890.
^ ^a ^b ^c ^d ^e Ball, Derek (2002), "Equiangular polygons", The Mathematical Gazette, 86 (507): 396–407, doi:10.2307/3621131, JSTOR 3621131, S2CID 233358516.

윌리엄스, R. 자연 구조의 기하학적 기초: 디자인 소스 북. 뉴욕: 도버 출판사, 1979. 페이지 32

외부 링크

등각 폴리곤의 특성: 그것은 무엇에 관한 것인가? 비비아니의 정리 Cut-the-knot에 대한 논의.
Weisstein, Eric W. "Equiangular Polygon". MathWorld.

[1] 마리우스 문테아누, 로라 문테아누, Rational Equiangular Polygons Applied Mathical, Vol.4 No.10, 2013년 10월

[ref1-2] Elias Abboud "On Viviani's Organization and the Extensions" 페이지 2, 11

[3] De Villiers, Michael, "Eqiangangular cyclic and quietronarycurrent polygons," Mathematical Gazette 95, 2011년 3월, 102-107년.

[4] 맥클린, K. 로빈. "등각형 다각형을 위한 강력한 대수 도구," 2004년 11월, Mathematical Gazette 88, 513-514.

[5] M. Bras-Amoros, M. Pujol: "Equiangular Polygons의 측면 길이"(코딩 이론가에게 보여짐), The American Mathematical Monthly, vol. 122, n. 5, 페이지 476–478, 2015년 5월. ISSN 0002-9890.

[ball-6] Ball, Derek (2002), "Equiangular polygons", The Mathematical Gazette, 86 (507): 396–407, doi:10.2307/3621131, JSTOR 3621131, S2CID 233358516.

[1]

[2]

[3]

[4]

[5]

[6]

Search

등각 다각형

네임스페이스

더

목차

건설

등각 다각형 정리

표기법

기타 속성

측면으로 직각형 다각형

등각 삼각형

등각형 사방측정감시

등각 펜타곤

등각형 육각형

등각 헵타곤

등각형 옥타곤

등각형 엔네아곤

등각형 데카곤

등각형 헨데카곤스

등각형 도데카곤

등각 테트라데카곤스

등각 펜타데카곤

등각형 육각형

등각형 옥타데카곤

등각형 이코사곤

참고 항목

참조

외부 링크