3-3 듀오프리즘

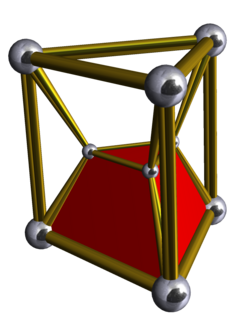3-3 듀오프리즘 슐레겔 도표
유형	균일 듀오프리즘
슐레플리 기호	{3}×{3} = {3}2
콕시터 다이어그램
세포	6 삼각 프리즘
얼굴	9개의 사각형, 삼각형 6개
가장자리	18
정점	9
정점수	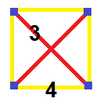사방형 디스페노이드
대칭	[3,2,3] = [6,2+,6], 주문 72
이중	3-3 듀오피라미드
특성.	볼록, 정점-정점-정점-변위-변위

4차원의 기하학에서 3-3 듀오프리즘 또는 삼각 듀오프리즘은 4차원 볼록 폴리스토프다.두 삼각형의 카르테시안 제품으로 구성할 수 있으며, 두 개의 폴리곤의 카르테시안 제품으로 구성된 무한 4차원 폴리토페즈 계열 중 가장 단순하다.

그것은 6개의 삼각 프리즘 세포에 9개의 정점, 18개의 가장자리, 15개의 면(정사각형 9개, 그리고 6개의 삼각형)을 가지고 있다.Coxeter 도표 와 대칭 [3,2,3], 순서 72가 있다.그것의 정점과 가장자리는 $3{\displaystyle \mathrm{}}$ ${\displaystyle \times }$ ${\displaystyle 3}$ $[\displaystyle 3\time$ 3}ruck의$$ 그래프를 형성한다.

하이퍼볼륨

3-3 듀오프리즘의 하이퍼볼륨은 가장자리 길이가 a인 V $4{\displaystyle {}_{}}$= 3 ${\displaystyle {16\mathrm{}}^{}}$ a 4 ${\$ 정삼각형의 면적의 $제곱{\displaystyle ,}$ ${\displaystyle \frac{A}{\mathrm{}}}$ = 3 ${\displaystyle {a\mathrm{}}^{}}$ = 2 ${\displaystyle a{}^{}}$ 2 ${\$^{}}}}}}}}{$3}{$3}$a^$2$\}\}.$

그래프

3-3 duoprism의 정점과 가장자리 그래프에는 9개의 정점과 18개의 가장자리가 있다.베를레캄프-반 린트-사이델 그래프와 콘웨이의 99그래프 문제에 대한 알 수 없는 해결책처럼, 모든 에지는 고유한 삼각형의 일부분이며 모든 비인접 쌍의 꼭지점은 고유한 사각형의 대각선이다.그것은 토로이드 그래프, 국소 선형 그래프, 매개변수가 있는 강력한 정규 그래프(9,4,1,2,3), $3{\displaystyle \mathrm{}}$ ${\displaystyle \times }$ ${\displaystyle 3}$ ${\displaystyle$ 3$\times 3}$ruck의$$ 그래프, 순서 9의 Paley 그래프다.^[1]This graph is also the Cayley graph of the group ${\displaystyle G=\langle a,b:a^{3}=b^{3}=1,\ ab=ba\rangle \simeq C_{3}\times C_{3}}$ with generating set ${\displaystyle S=\{a,a^{2},b,b^{2}\}}$.

이미지들

직교 투영

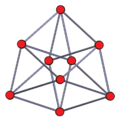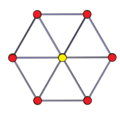그물	2회 회전으로 3D 투시 투영

대칭

5차원에서는 일부 균일한 5-폴리탑은 3-3 듀오프리즘 정점 수치를 가지며, 일부 균일한 5-폴리탑은 가장자리 길이가 동일하지 않고 따라서 대칭이 더 낮은 경우도 있다.

대칭	[[3,2,3]], 주문 72	[3,2, 주문 12]
콕시터 도표를 만들다
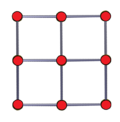
슐레겔 도표를 만들다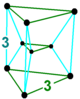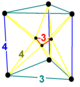
이름	α25	α035	t035	t03β5

양방향 16셀 벌집도 3-3 듀오프라즘 정점 수치를 갖고 있다.아래 대칭이 두 개 있는 벌집형 구조는 세 개 있다.

대칭	[3,2,3, 주문 36]	[3,2, 주문 12]	[3], 주문 6
콕시터 도표를 만들다
스큐 직교적 투영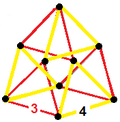

관련 복합 폴리곤

$C{\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {\mathrm{}}^{}}$ ${\$의 일반 복합 폴리토프 {4},₂ 4차원 공간에서 3-3 듀오프리즘으로 실제 표현된다$$.₃{4}₂은(는) 9개의 정점과 6개의 3개의 정점을 가지고 있다.그것의 대칭은 [4]₂ 순서 18이다.또한 대칭 [2],₃ 순서 9를 갖는 더 낮은 대칭 구조, 또는 {}×{}×{}}₃를 가지고 있다.빨간색과 파란색 3-에지가 구별되는 경우 대칭이다.^[2]

투시 투영

중심 정점과 일치하는 직교 투영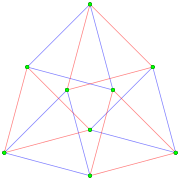

직교 투영, 요소 중첩을 방지하기 위한 간격띄우기 뷰.

관련 폴리토페스

k₂₂ n차원의 숫자

공간	유한한			유클리드 주	쌍곡선
n	4	5	6	7	8
콕시터 무리를 짓다	A2A2	E6	${\displaystyle {\stackrel{}{E}}_{}}$~ ${\displaystyle 6_{\mathrm{}}}$ ${\$ =E6+	${\displaystyle {\stackrel{\text{'}}{T}7}_{\mathrm{}}}$ ${\$ $=$E6++
콕시터 도표를 만들다
대칭	[[32,2,-1]]	[[32,2,0]]	[[32,2,1]]	[[32,2,2]]	[[32,2,3]]
주문	72	1440	103,680	∞
그래프				∞	∞
이름	−122	022	122	222	322

3-3 듀오피라미드

3-3 듀오피라미드
유형	균일 듀얼 듀오피라미드
슐레플리 기호	{3}+{3} = 2{3}
콕시터 다이어그램
세포	9개의 4각형 디스페노이드
얼굴	이등변 삼각형 18개
가장자리	15 (9+6)
정점	6 (3+3)
대칭	[3,2,3] = [6,2+,6], 주문 72
이중	3-3 듀오프리즘
특성.	볼록, 정점-정점-정점-변위-변위

3-3 duoprism의 이중은 3-3 duopyramid 또는 삼각 duopramid라고 불린다.4각형 디스페노이드 세포 9개, 삼각면 18개, 가장자리 15개, 꼭지점 6개가 있다.

직교 투영에서는 정점의 6곤 원과 투영에서 볼 수 있는 5-심플렉스처럼 모든 쌍을 연결하는 가장자리를 볼 수 있다.

정사영

관련 복합 폴리곤

일반 복합 폴리곤 {4}₃은(는) $C{\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {\mathrm{}}^{}}$ ${\$}}에 6개의 정점을 가지며, R$$ ${\displaystyle {\mathrm{}}^{}}$ ${\$^$4}$은 3-3 듀오피라미드의 동일한 정점 배열과 일치한다$$.3-3 듀오피라미드의 연결 가장자리에 해당하는 9개의 2-edge가 있으며, 2개의 삼각형을 연결하는 6개의 가장자리는 포함되지 않는다.색상의 가장자리 3세트를 가진 육각형 투영에서 볼 수 있다.정점과 가장자리의 배열을 통해 하나의 삼각형에서 각 꼭지점이 다른 하나의 꼭지점에 연결되는 완전한 양립자 그래프를 만든다.그것은 톰슨 그래프 또는 4-케이지라고도 불린다.^[3]

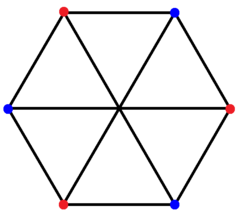파란색과 빨간색으로 6개의 정점이 있는 {4}3은(는) 9개의 2-에지로 연결되어 완전한 초당적 그래프로 표시된다.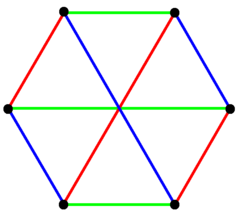

그것은 3개의 가장자리 세트로 이루어져 있으며, 여기서 컬러로 볼 수 있다.

참고 항목

• 3-4 듀오프리즘
• 테세락트 (4-4 듀오프리즘)
• 5-5 듀오프리즘
• 볼록 정규 4폴리토프
• 듀오실린더

메모들

참조

• 일반 폴리토페스, H. S. M. Coxeter, Dover Publishments, Inc., 1973, New York, 124 페이지.
• 콕시터, 기하학의 아름다움: 12편의 에세이, 도버 출판물, 1999년 ISBN0-486-40919-8(3장 4차원의 일반 스큐 폴리헤드라와 그 위상학적 유사성)
  • Coxeter, H. S. M. 정규 스큐 3차원 및 4차원 폴리헤드라.Proc. 런던 수학.Soc. 43, 33-62, 1937.
• 존 H. 콘웨이, 하이디 버기엘, 차임 굿맨-스트라스, 2008년 사물의 대칭성, ISBN 978-1-56881-220-5 (제26장)
• Norman JohnsonUniform Polytopes, 원고(1991)
  • N.W. 존슨:균일다각체와 허니컴의 이론, 박사학위.1966년 토론토 대학교의 논문
• 볼록스 폴리초라 목록, 제6장 조지 올셰프스키.
• 아폴로니아 볼 패킹과 스택형 폴리토페스 이산 & 계산 기하학, 2016년 6월, 제55권, 제4권, 페이지 801–826

외부 링크

• 간단히 설명된 네 번째 차원—듀오프라임을 "이중 프리즘"으로, 듀오킬린더를 "이중 실린더"로 설명
• 폴리글로스 – 고차원 용어의 용어집
• 기하학적 제품을 사용한 하이퍼스페이스 탐색