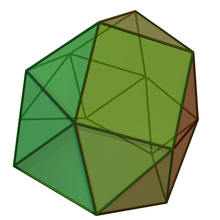
자이로평방형 삼각형

자이로평방형 삼각형
유형	존슨 J21 - J22 - J23
얼굴	1+3x3+6 삼각형 정사각형 3개 육각형 1개
가장자리	33
정점	15
꼭지점 구성	3(3.4.3.4) 2.3(33.6) 6(34.4)
대칭군	C3v
이중 다면체	-
특성.	볼록하게 하다
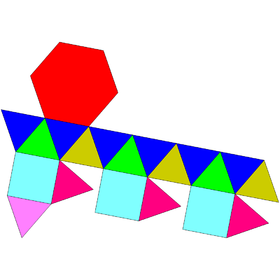
그물

기하학에서, 길쭉한 삼각형 큐폴라는 존슨 고형물(J₂₂)의 하나이다.삼각 큐폴라(J₃) 밑면에 육각형 항정신병증을 부착해 시공할 수 있다.이것을 "균형화"라고 하는데, 이는 항정신병증이 고체의 기저부, 또는 둘 이상의 고체의 기저부 사이에 결합된다는 것을 의미한다.

또한, 삼각형 큐폴라는 하나의 삼각형 큐폴라가 제거된 회전형 삼각형 바이쿠폴라(J₄₄)로 볼 수 있다.모든 큐폴레와 마찬가지로 베이스 폴리곤은 위쪽에 비해 면이 2배(이 경우, 아래 폴리곤은 위가 삼각형이기 때문에 육각형이다).

존슨 고체는 일반 폴리곤 면으로 구성되지만 균일한 폴리헤드라(Platonic 고형물, 아르키메데스 고형물, 프리즘 또는 항정신병)가 아닌 92개의 엄격히 볼록한 폴리헤드라 중 하나이다.그것들은 1966년에 처음으로 이 다면체들을 나열한 노먼 존슨이 이름을 지었다.^[1]

포뮬라과

모든 면이 정규이고 가장자리 길이가 a인 경우 부피 및 표면적에 대해 다음과 같은 공식을 사용할 수 있다.^[2]

${\displaystyle V=\좌({\frac {1}{3}{\sqrt{61}{2}}+18{\sqrt{3}}}}{1+{\sqrt{3}}}}}}}}{3}}}}\약 3.51605...a^{3}}$

${\displaystyle A=\왼쪽(3+{\frac {11{\sqrt{3}}{2}}\\오른쪽)a^{2}\약 12.5263...a^{2}}:$

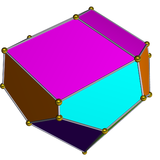
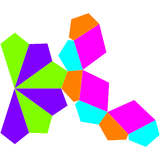
이중 다면체

세모난 삼각 큐폴라의 이중은 15개의 얼굴을 가지고 있다: 연 6개, 롬비 3개, 펜타곤 6개.

이중 회전 삼각 큐폴라	이중 그물

참조

외부 링크

• Eric W. Weisstein, Gyroelongated triangular cupola (Johnson solid) at MathWorld.