길쭉한 삼각 큐폴라

길쭉한 삼각 큐폴라
유형	존슨 J17 - J18 - J19
얼굴	1+3 삼각형 3x3 정사각형 육각형 1개
가장자리	27
정점	15
꼭지점 구성	6(42.6) 3(3.4.3.4) 6(3.43)
대칭군	C3v
이중 다면체	-
특성.	볼록하게 하다
그물

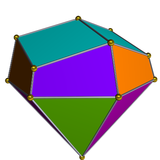
기하학에서 길쭉한 삼각 큐폴라는 존슨 고형물(J₁₈)의 하나이다.이름에서 알 수 있듯이 밑면에 육각 프리즘을 붙여 삼각형 큐폴라(J₃)를 길게 하여 시공할 수 있다.

존슨 고체는 일반 폴리곤 면으로 구성되지만 균일한 폴리헤드라(Platonic 고형물, 아르키메데스 고형물, 프리즘 또는 항정신병)가 아닌 92개의 엄격히 볼록한 폴리헤드라 중 하나이다.그것들은 1966년에 처음으로 이 다면체들을 나열한 노먼 존슨이 이름을 지었다.^[1]

포뮬라과

모든 면이 정규이고 가장자리 길이가 a인 경우 부피 및 표면적에 대해 다음과 같은 공식을 사용할 수 있다.^[2]

${\displaystyle V=\left({\frac {1}{6}}}\왼쪽(5{\sqrt{2}}+9}{\sqrt{3}\오른쪽)a^{3}\ 약 3.77659...a^{3}}$

${\displaystyle A=\왼쪽(9+{\frac {5{\\sqrt{3}}}{2}}\오른쪽)a^{2}\약 13.3301...a^{2}}:$

이중 다면체

길쭉한 삼각 큐폴라의 이중은 이등변 삼각형 6개, 롬비 3개, 사분변측정학 6개 등 15개의 면으로 되어 있다.

이중 신장 삼각 큐폴라	이중 그물

관련 다면체 및 허니컴

길쭉한 삼각 큐폴라는 네모난 피라미드와 네모난 피라미드로 공간을 다듬을 수 있다.^[3]

참조

외부 링크

• Eric W. Weisstein, Elongated triangular cupola (Johnson solid) at MathWorld.