3-7키스롬빌

3-7키스롬빌
3-7키스롬빌
유형	이중 반정형 쌍곡선 타일링
얼굴	직삼각형
가장자리	무한
정점	무한
콕시터 다이어그램
대칭군	[7,3], (*732)
회전군	[7,3]+, (732)
이중 다면체	잘린 3헥타르 정사각형 타일
면 구성	V4.6.14
특성.	면직의

기하학에서 3-7키스롬빌 타일링은 쌍곡면의 반정형 이중 타일링이다. 각 꼭지점에서 4개, 6개, 14개의 삼각형이 만나는 합치 우측 삼각형으로 구성된다.

이미지는 쌍곡면의 푸앵카레 디스크 모델 투영을 보여준다.

각 직각 삼각형 면은 정점의 세 가지 유형을 가지고 있기 때문에 V4.6.14라고 표시된다. 하나는 4개의 삼각형이 있고, 하나는 6개의 삼각형이 있고, 다른 하나는 14개의 삼각형이 있다. 그것은 각 꼭지점에 1개의 정사각형과 1개의 헵타곤, 1개의 4각각형이 있는 잘린 3각형 타일링의 이중 테셀레이션이다.

이름 지정

3-7 kisrhombille이라는 이름은 콘웨이가 붙여준 이름인데, 3-7 롬빅 타일링으로 보고, 키스 오퍼레이터에 의해 나누어져 각 롬버스에 중앙점을 더하고, 4개의 삼각형으로 나누어져 있다.

대칭

[7,3]의 미러 제거 하위 그룹은 없다. 유일한 작은 지수 부분군은 교대, [7,3],⁺ (732)이다.

[7,3], (*732)의 작은 인덱스 하위 그룹
유형	반사적	회전
색인을 달다	1	2
도표
콕시터 (svifold)	[7,3] = (*732)	[7,3]⁺ = (732)

관련 다면체 및 틸팅

3개의 등면(일반 또는 quasiregular) 기울기는 삼각형을 결합하여 이 타일링에서 구성할 수 있다.

여러 삼각형 점을 중심으로 한 투영
중심	헵타곤	삼각형	롬빅
푸앵카레 원반 본을 뜨다
클라인 원반 본을 뜨다
관련 타일링
관련 타일링	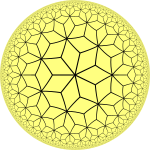헵타곤 타일링	삼각 타일링	롬빅 타일링

균일한 헵탄/삼각형 틸팅 v t
대칭: [7,3], (*732)							[7,3]⁺, (732)


{7,3}	t{7,3}	r{7,3}	t{3,7}	{3,7}	rr{7,3}	tr{7,3}	sr{7,3}
균일 듀얼


V7³	V3.14.14	V3.7.3.7	V6.6.7	V3⁷	V3.4.7.4	V4.6.14	V3.3.3.3.7

그것은 다면체 수열과 토폴로지적으로 관련이 있다. 토론을 참조하라. 이 그룹은 정점당 모든 가장자리 수를 가지며 평면의 다면선과 무한선을 통해 이등분 평면을 형성하는 데 특별하며, 중요한 (2,3,7) 삼각형 그룹인 헵각형 타일링에 대한 (2,3,7) 삼각형 그룹에 대한 반사 영역이다.

대칭이 (2,3,7)인 쌍곡면의 균일한 기울기를 참조하십시오.

키스롬빌 기울기는 정육면체부터 시작하여 얼굴 중심점에 의해 모서리에 얼굴이 나누어져 있거나 키스를 하는 롬빌 기울기의 순서에서 볼 수 있다.

n32 전분해 틸팅의 대칭 변이: 4.6.2n* v t
Sym. *n32 [n,3]	구면				유클리드	콤팩트 하이퍼브.		파라코.	비대칭 쌍곡선
Sym. *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
수치
구성.	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
듀얼스
구성.	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.1987	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i