삼각군

수학에서 삼각형 집단은 삼각형의 측면을 가로지르는 반사의 순서에 의해 기하학적으로 실현될 수 있는 집단을 말한다.삼각형은 일반적인 유클리드 삼각형, 구상의 삼각형 또는 쌍곡 삼각형이 될 수 있다.각 삼각형 그룹은 뫼비우스 삼각형이라고 불리는 응집 삼각형에 의한 유클리드 평면, 구면 또는 쌍곡면의 타일링의 대칭 그룹이며, 각각은 작용의 기본 영역이다.null

정의

l, m, n을 2보다 크거나 같은 정수로 한다.삼각형 그룹 Δ(l,m,n)는 각도 π/l, π/m, π/n(라디안으로 측정)을 가진 삼각형 측면의 반사에 의해 생성된 유클리드 평면, 2차원 구체, 실제 투영 평면 또는 쌍곡면의 움직임 그룹이다.인접한 두 변의 반사의 산물은 각도에 의한 회전이며, 각도는 2㎛, 2㎛, 2㎛/n이다.따라서 생성되는 반사에 a, b, c라는 라벨이 붙고 그 사이의 각도가 위에서 설명한 것과 같은 경우 다음과 같은 관계가 유지된다.

1. ${\displaystyle a^{2}=b^{2}=c^{2}=1}$
2. ${\displaystyle (ab)^{l}=(bc)^{n}=(ca)^{m}=1.}$

a, b, c 사이의 다른 모든 관계는 이러한 관계의 결과라는 것과 Δ(l,m,n)는 해당 공간의 별개의 움직임 그룹이라는 것이 정리다.따라서 삼각형 그룹은 그룹 프레젠테이션을 인정하는 반사 그룹이다.

${\displaystyle \Delta (l,m,n)=\langle a,b,c\mid a^{2}=b^{2}=c^{2}=(ab)^{l}=(bc)^{n}=(ca)^{m}=1\rangele .}$

이 프레젠테이션이 포함된 추상 그룹은 세 개의 생성자를 가진 Coxeter 그룹이다.null

분류

어떤 자연수 l, m, n > 1 정확히 고전적인 2차원 기하학(유클리드, 구면 또는 쌍곡)의 하나로서 각도가 있는 삼각형(π/l, π/m, π/n)을 인정하고, 공간은 삼각형의 반사로 타일화된다.삼각형의 각도의 합은 가우스-보넷 정리(Gauss-Bonnet organ)에 의해 기하학의 유형을 결정한다: 각도 합이 정확히 π이면 유클리드, π을 넘으면 구형, spherical보다 엄격히 작으면 쌍곡선이다.더욱이 주어진 각도를 가진 두 개의 삼각형들은 모두 합치된다.각 삼각형 그룹은 타일링을 결정하는데, 타일은 일반적으로 두 가지 색상으로 색칠되어 있어서, 인접한 두 타일은 모두 반대 색상을 갖는다.null

숫자 l, m, n > 1에 관해서는 다음과 같은 가능성이 있다.null

유클리드 사건

${\displaystyle {\frac{1}{l}+{\frac {1}{m}+{\frac {1}{n}=1.}$

삼각형 집단은 각도가 ((또는 180°)에 이르는 삼각형에 의해 유클리드 평면의 특정 테셀레이션(또는 타일링)의 무한대칭 집단을 말한다.순열까지 3중(l, m, n)은 3중(2,3,6), (2,4,4), (3,3)중 하나이다.해당 삼각형 그룹은 배경화면 그룹의 인스턴스다.null

(2,3,6)	(2,4,4)	(3,3,3)
이등분된 육각 타일링	테트라키스 네모난 타일링	삼각 타일링
정점에 레이블을 지정하고 반사가 작동하는 방식을 보여주는 더 자세한 다이어그램:

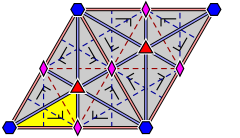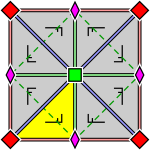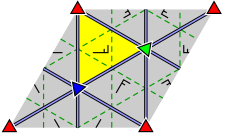구면 케이스

${\displaystyle {\frac{1}{l}+{\frac {1}{m}+{\frac {1}{n}}}1.}$

삼각형 그룹은 구면 삼각형 또는 뫼비우스 삼각형에 의한 단위 구체의 타일링의 유한 대칭 그룹으로, 각도는 π보다 큰 숫자로 합산된다.순열까지, 삼중(l,m,n)형태(2,3,3),(2,3,4),(2,3,5)또는(2,2,n), n>1 가지고 있다.구면 삼각형 그룹 정기적인 다면체의 3차원 유클리드 공간의 대칭들과:Δ(2,3,3)의 4면체, Δ(2,3,4)둘 다 큐브가 동일한 대칭 g을 가지고 있는 8면체(에 해당합니다 확인할 수 있습니다도두면체 및 이도면체 모두에 대해 Δ(2,3,5)를 측정한다.이면 대칭의 Δ(2,2,n), n > 1 그룹은 두 개의 동일한 정규 n-곤이 함께 결합하여 형성된 퇴행성 고형분인 디헤드라 계열의 대칭군 또는 두 꼭지점에서 n 디곤을 함께 결합하여 형성된 다면 호소헤드라 계열의 대칭군으로 해석할 수 있다.null

일반 다면체에 해당하는 구면 타일링은 다면체의 편심 소분법을 형성하고 그 결과로 생긴 점과 선을 한정된 구면에 투영함으로써 얻는다.사면체의 경우 4면이 있으며, 각 면은 중앙에서 교차하는 중위수에 의해 6개의 작은 조각으로 세분되는 정삼각형이다.그 결과 테셀레이션은 4 × 6=24개의 구형 삼각형(구형 디스다이나키스 큐브)을 가지고 있다.null

이러한 그룹은 구의 압축성에 해당하는 유한하다. – 구내의 디스크 영역은 처음에는 반지름 면적으로 성장하지만, 결국 전체 구를 덮는다.null

삼각형 기울기는 다음과 같다.

(2,2,2)	(2,2,3)	(2,2,4)	(2,2,5)	(2,2,6)	(2,2,n)
(2,3,3)		(2,3,4)		(2,3,5)

팔면체 및 이코사면체에 해당하는 구형 틸팅과 짝수 n이 있는 편면 구형 틸팅은 중심 대칭이다.따라서 이들 각각은 실제 투사 평면의 타원 타원 타원 타일링(tiling))을 결정한다.그것의 대칭군은 순서 2의 중심 요소인 원점(-I)을 통한 반사에 의한 구면 삼각형 집단의 몫이다.투영면은 타원형 기하학의 모형이기 때문에 그러한 그룹을 타원형 삼각형 그룹이라고 한다.^[1]null

쌍곡선 케이스

${\displaystyle {\frac{1}{l}+{\frac {1}{m}+{\frac {1}{n}}<1.}$

삼각형 그룹은 각도가 π보다 작은 숫자에 이르는 쌍곡선 삼각형에 의한 쌍곡면 타일링의 무한대칭 그룹이다.아직 나열되지 않은 모든 세 쌍은 쌍곡면의 기울기를 나타낸다.예를 들어, 삼중(2,3,7)은 (2,3,7) 삼각형 그룹을 생성한다.그러한 집단은 무한히 많다; 약간의 작은 값과 관련된 기울기:

쌍곡면

기본 도메인 삼각형의 푸앵카레 디스크 모델

오른쪽 삼각형 예제(2p q)
(2 3 7)	(2 3 8)	(2 3 9)	(2 3 ∞)
(2 4 5)	(2 4 6)	(2 4 7)	(2 4 8)	(2 4 ∞)
(2 5 5)	(2 5 6)	(2 5 7)	(2 6 6)	(2 ∞ ∞)
일반 삼각형 예제(p q r)
(3 3 4)	(3 3 5)	(3 3 6)	(3 3 7)	(3 3 ∞)
(3 4 4)	(3 6 6)	(3 ∞ ∞)	(6 6 6)	(∞ ∞ ∞)

쌍곡선 삼각형 그룹은 비유클리드 그룹의 예로서 그로모프 쌍곡선 그룹 이론에서 일반화되었다.null

폰 다이크 그룹

발전기에서 짝수 길이의 단어로 생성된 Δ(l,m,n)에서 지수 2의 부분군을 D(l,m,n)로 나타낸다.그러한 하위집단은 발터 폰 다이크의 이름을 따서 "일반적인" 삼각집단^[2] 또는 폰 다이크 집단이라고 부르기도 한다.구면, 유클리드, 쌍곡 삼각형의 경우, 이것들은 삼각형의 방향, 즉 회전 그룹의 방향을 보존하는 그룹의 원소에 해당한다.투사형(엘립틱) 삼각형의 경우 투사면이 방향성이 없으므로 "방향 보존"이라는 개념이 없기 때문에 그렇게 해석할 수 없다.그러나 반사는 국소 방향 반향이다(그리고 모든 다지관은 국소 방향 반향이다, 국소적 유클리드: 국소적 유클리드: 그들은 선을 고정하고 선의 각 지점에서 선을 가로질러 반사된다).^[3]null

그룹 D(l,m,n)는 다음 프레젠테이션으로 정의된다.

${\displaystyle D(l,m,n)=\langle x,y\mid x^{l},y^{m},(xy)^{n}\angle .}$

위의 발전기로 볼 때, 이것들은 x = ab, y = ca, yx = cb이다.기하학적으로 세 원소 x, y, xy는 삼각형의 꼭지점 3개에 대하여 2㎛/l, 2㎛, 2㎛/n씩 회전하는 것에 해당한다.null

D(l,m,n) ≅ D(m,l,n) ≅ D(n,m,l) ≅ D(l,m,n)는 l,m,n의 순서와 무관하다는 점에 유의한다.

쌍곡선 폰 다이크 그룹은 쌍곡면의 방향 유지 등위계로 구성된 이산형 그룹인 푸치안 그룹이다.null

겹경사

삼각형 그룹은 뫼비우스 삼각형이라고 불리는 작용(반사의 선으로 정의되는 삼각형)의 기본 영역인 삼각형 별 타일링을 보존하고 있으며, 정수는 정점에 모여 있는 (2l,2m,2n) 삼각형에 해당하는 세 개의 정수(l,m,n)에 의해 주어진다.합리적인 숫자(l/a,m/b,n/c)로 슈바르츠 삼각형에 해당하는 삼각형을 겹쳐서 기울이는 것도 있는데, 여기서 분모는 분자와 동일시된다.이는 aπ/l (resp.)의 각도에서 만나는 에지에 해당하며, 이는 순서 l을 가지고 있고 따라서 추상적인 그룹 요소로서 동일하지만 반사로 표현될 때 구별되는 2a³/l (resp.)의 회전에 해당한다.null

예를 들어 슈바르츠 삼각형(2 3 3)은 구의 밀도 1 타일링을, 삼각형(2 3/2)은 구의 밀도 3 타일링을 산출하지만, 추상적인 그룹은 동일하다.기울기가 겹치는 이러한 대칭은 삼각형 그룹으로 간주되지 않는다.null

역사

삼각형 집단은 적어도 1856년 윌리엄 로완 해밀턴에 의한 (회전) (2,3,5) 삼각 집단으로서 이코시안 미적분학에 관한 논문에서 이코사이드 집단의 발표까지 거슬러 올라간다.^[4]null

적용들

외부 영상
뒤틀린 모듈식 타일링[5] – 관련 틸팅을 모핀하여 지도(2,3,3,7) → (2,3,7)의 시각화.

삼각형 그룹은 산술 기하학에서 발생한다.그 모듈형 그룹 두가지 요소, S, T, S²)=1(T에 관계 없)(ST)³의 관계에 따라 모든 삼각형 그룹(2,3,n)중성자 온도=1, 보다 일반적으로 헤케 그룹 Hq 두가지 요소, S, T, 관계를 S2에 의거)에 의해 만들어진다(ST)q 관계=1( 없r를 첨가하여 위로는 회전 삼각형 그룹(2,3,∞) 와 지도에 의해 만들어진다elation on T)는 회전 삼각형 그룹(2,q,320)이며, Tⁿ = 1 관계를 추가하여 모든 삼각형 그룹(2,q,n)에 매핑된다. 모듈형 그룹은 Heck 그룹이다₃.그로텐디크의 데신 덴판트 이론에서 벨리 함수는 삼각형 그룹의 반사 영역에 의해 리만 표면의 테셀레이션을 발생시킨다.null

산발적인 26개 그룹은 모두 삼각형 그룹의 몫이며,^[6] 이 중 12개 그룹은 허위츠 그룹(2,3,7)이다.null

참고 항목

• 슈바르츠 삼각형
• 슈바르츠 삼각지도는 위쪽 반면에 대한 삼각형의 지도다.
• 기하군 이론

참조

이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "트리앵글 그룹" – 뉴스 · 신문 · 책 · 학자 · JSTOR (2010년 4월) (이 템플릿 메시지를 제거하는 방법과 시기 학습)

외부 링크

• 로버트 도슨 일부 구면 기울기(unted, 2004년 이전) (여러 가지 흥미로운 구면 기울기를 나타내며, 대부분은 삼각형 그룹 기울기가 아니다.)
• Elizabeth r Chen 삼각형 그룹(2010) 바탕 화면 배경 사진

이 글에는 크리에이티브 커먼스 귀속/공유-알리케 라이센스에 따라 라이센스가 부여된 PlanetMath의 트라이앵글 그룹의 자료가 통합되어 있다.