웨이브릿

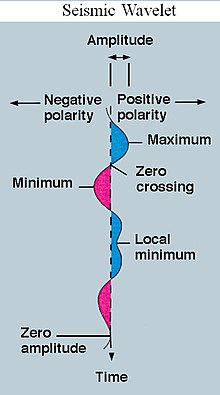
웨이브릿은 진폭이 0에서 시작하여 증가 또는 감소하다가 한 번 이상 0으로 돌아오는 파동 같은 진동입니다.웨이브릿은 "단순 진동"이라고 불립니다.맥박의 수와 방향에 따라 웨이브릿 분류법이 확립되었습니다.웨이브릿에는 신호 처리에 유용한 특정 특성이 포함되어 있습니다.

지진파

예를 들어, 중간 C의 주파수와 약 10분의 1초의 짧은 지속 시간을 가지도록 웨이브렛을 생성할 수 있습니다.이 웨이브릿을 멜로디의 녹음으로부터 생성된 신호로 컨볼루션 할 경우, 그 결과 신호는 곡에 미들 C 음이 언제 나타났는지를 결정하는 데 도움이 될 것이다.수학적으로 웨이브릿은 신호의 일부가 유사한 경우 신호와 상관합니다.상관관계는 많은 실용적인 웨이브릿 애플리케이션의 핵심입니다.

수학적 도구로서 웨이브렛은 오디오 신호와 이미지를 포함한 다양한 종류의 데이터에서 정보를 추출하는 데 사용할 수 있습니다.데이터를 완전히 분석하려면 웨이브릿 세트가 필요합니다."보완적" 웨이브릿은 분해 과정이 수학적으로 가역적이도록 간격이나 겹침 없이 신호를 분해합니다.따라서, 상보적인 웨이브릿 세트는 최소한의 손실만으로 원래의 정보를 회복하는 것이 바람직한 웨이브릿 기반의 압축/압축 해제 알고리즘에서 유용합니다.

형식적으로 표현하면, 이 표현은 정사각형 적분함수의 힐베르트 공간에 대한 완전한 직교정규함수 집합 또는 벡터 공간의 과잉 집합 또는 프레임에 관한 정사각형 적분함수의 웨이브릿 급수 표현이다.이것은 일관성 있는 상태를 통해 달성됩니다.

고전 물리학에서 회절 현상은 전파 파면의 각 점을 개별 구면 웨이브릿의 ^[1]집합으로 처리하는 호이겐스-프레스널 원리에 의해 설명된다.특징적인 굽힘 패턴은 간섭성 소스(레이저 등)로부터의 파장이 파장에 필적하는 슬릿/어퍼처와 조우할 때 가장 두드러집니다.이는 다른 길이의 경로를 통해 레지스터 표면에 이동하는 파면(또는 동등한 각 웨이브릿)의 서로 다른 포인트가 추가 또는 간섭되기 때문입니다.여러 개의 촘촘한 간격의 개구부(예: 회절 격자)는 다양한 강도의 복잡한 패턴을 초래할 수 있다.

어원학

웨이브릿이라는 단어는 디지털 신호 처리와 탐사 지구 ^[2]물리학에서 수십 년 동안 사용되어 왔다."작은 파도"를 뜻하는 프랑스어 온델레트는 1980년대 초 몰레와 그로스만에 의해 사용되었다.

웨이브릿 이론

웨이브릿 이론은 몇 가지 주제에 적용할 수 있다.모든 웨이브릿 변환은 연속 시간(아날로그) 신호에 대한 시간 주파수 표현의 형태로 간주될 수 있으므로 고조파 분석과 관련이 있습니다.다이애딕(옥타브 밴드) 구성의 이산 시간 필터 뱅크를 사용한 이산 시간(샘플링) 신호의 이산 웨이브릿 변환(시간 내 연속)은 해당 신호에 대한 웨이브릿 근사치이다.이러한 필터 뱅크의 계수를 웨이브릿 명명법에서는 시프트 및 스케일링 계수라고 합니다.이러한 필터 뱅크에는 유한 임펄스 응답(FIR) 또는 무한 임펄스 응답(IIR) 필터가 포함되어 있을 수 있습니다.연속 웨이브 렛 변환(CWT)을 형성하는 웨이브 렛은 푸리에 분석의 불확도 원리에 따라 달라집니다.어떤 이벤트가 포함된 신호가 주어지면 그 이벤트에 정확한 시간과 주파수 응답 스케일을 동시에 할당할 수 없습니다.시간 및 주파수 응답 척도의 불확실성의 곱은 하한을 갖는다.따라서 이 신호의 연속 웨이브릿 변환 스케일그램에서 이러한 이벤트는 시간 스케일 평면의 한 지점이 아닌 전체 영역을 표시합니다.또한 이산 웨이브릿 베이스는 불확실성 ^[3]^[4]^[5]^[6]원리의 다른 형태의 맥락에서 고려될 수 있다.

웨이브릿 변환은 크게 연속, 이산 및 다중 해상도 기반의 세 가지 클래스로 나뉩니다.

연속 웨이브릿 변환(연속 시프트 및 스케일 파라미터)

연속 웨이브릿 변환에서는 유한 에너지의 주어진 신호가 연속 주파수 대역 패밀리(또는 L 함수^p 공간² L(R)의 유사한 부분 공간)에 투영됩니다.예를 들어 신호는 모든 양의 주파수 f > 0에 대해 [f, 2f] 형식의 모든 주파수 대역에서 나타낼 수 있습니다.그런 다음, 결과적인 모든 주파수 성분에 대해 적절한 통합을 통해 원래 신호를 재구성할 수 있습니다.

주파수 대역 또는 하위 공간(하위 밴드)은 스케일 1에서 하위 공간의 스케일 버전입니다.이 부분공간은 대부분의 상황에서 모 웨이브릿인 L(R)에서 하나의² 생성함수 θ의 이동에 의해 생성됩니다.스케일 1 주파수 대역 [1, 2]의 예에서 이 함수는 다음과 같습니다.

\psi(t)=2,\operatorname {filename}(2t)-,\operatorname {filename}(t)=flac {sin(2\pi t)-\sin(\pi t)}{\pi t}

(정규화된) sync 함수를 사용합니다.Meyer's와 다른 두 가지 어머니 웨이브릿의 예는 다음과 같습니다.

마이어

모레

멕시코 모자

척도의 부분 공간 또는 주파수 대역[1/a, 2/a]기능을(가끔 아이 wavelets라고 불리는)에 의해 만들어진다.

\displaystyle \psi _{a,b}(t)=snap frac {1}{\snaphrt {a}}\psi \snaph\frac {t-b}{a}}\right}}}}

어디고가 손상되고 이동을 정의하는 규모와 b는 어떤 실수를 정의합니다 긍정적이다.그 한쌍(a, b)오른쪽 halfplane R+에 × 점 R을 정의합니다

함수의 규모의 부분 공간에 돌출부)이 있는 형태이다.

\displaystyle x_{a}(t)=\int _{\mathbb {R}}WT_{\psi }\{x\}(a,b)\cdot \psi _{a,b}(t),db}

작은 파도 계수

\displaystyle WT_{\psi }\{x\}(a,b)=\displayle x,\psi _{a,b}\rangle =\int _{\mathbb {R}}x(t){\psi _{a,b}(t)},dt.}

신호 x의 해석은 웨이브릿 계수를 신호의 스케일그램으로 조합할 수 있다.

일부 연속 웨이브릿 목록을 참조하십시오.

이산 웨이브릿 변환(이산 시프트 및 스케일 파라미터, 시간 내 연속)

모든 웨이브릿 계수를 사용하여 신호를 분석하는 것은 계산적으로 불가능하기 때문에 대응하는 웨이브릿 계수에서 신호를 재구성하기 위해 상부 하프플레인의 이산 서브셋을 선택하는 것이 충분한지 궁금할 수 있습니다.이러한 시스템 중 하나는 a > 1, b > 0의 실제 파라미터에 대한 아핀 시스템입니다.하프플레인의 해당 이산 서브셋은 z 단위의 m, n이 있는 모든 점(a^m, nb^m a)으로 구성됩니다.해당하는 하위 웨이브릿은 다음과 같이 제공됩니다.

(\displaystyle \psi _{m,n}(t)=paramfrac {1}{\paramrt {a^{m}}}\psi \leftfarc\frac {t-nba^{m}}}{a^{m}}}\오른쪽).}

다음 공식에 의한 유한 에너지의 신호 x의 재구성을 위한 충분한 조건

\displaystyle x(t)=\sum _{m\in \mathbb {Z}\sum _{n\in \mathbb {Z}}\sum x,\psi _{m,n}\rangle \cdot \psi _{m,n}(t)}\sum

함수

\{\psi _{m,n}:m,n\in \mathbb {Z} \}

{

\{\psi _{m,n}:m,n\in \mathbb {Z} \}

m

\{\psi _{m,n}:m,n\in \mathbb {Z} \}

、

\{\psi _{m,n}:m,n\in \mathbb {Z} \}

:

\{\psi _{m,n}:m,n\in \mathbb {Z} \}

、

\{\psi _{m,n}:m,n\in \mathbb {Z} \}

Z

}

{

displaystyle

\ { \

psi

_ {

m

,

n }

: m , n \

in

\

mathbb

{

Z }

\ }이 L(R

\{\psi _{m,n}:m,n\in \mathbb {Z} \}

)의² 직교 정규 기저를 형성하는 것입니다.

다중 해상도 기반 이산 웨이브릿 변환(시간 내 연속)

D4 웨이브릿

모든 이산화된 웨이브릿 변환에서는 상부 하프플레인의 각 경계 직사각형 영역에 대해 한정된 수의 웨이브릿 계수만 존재합니다.그러나 각 계수는 적분을 평가해야 합니다.특수한 상황에서 스케일링 및 시프트된 웨이브릿이 다중 분해능 분석을 형성하면 이러한 수치 복잡성을 피할 수 있다.즉, L(R)에² 아버지 웨이브릿θ라는 보조함수가 존재해야 하며 a는 정수임을 의미합니다.일반적인 선택은 a = 2 및 b = 1입니다.가장 유명한 아버지와 어머니 웨이브렛은 Daubechies 4탭 웨이브렛입니다.모든 직교 정규 이산 웨이브릿 기준이 다중 해상도 분석과 연관될 수 있는 것은 아닙니다. 예를 들어 Journe 웨이브렛은 다중 해상도 ^[7]분석을 허용하지 않습니다.

엄마와 아빠의 웨이브릿에서 서브스페이스를 구축한다.

\displaystyle V_{m}=\operatorname {span}(\phi _{m,n:n\in \mathbb {Z}), {\text{여기}}\phi _{m,n}(t)=2^{-m/2}\phi(2^{-m}t-n)})}

\displaystyle W_{m}=\operatorname {span}(\psi _{m,n:n\in \mathbb {Z}), {\text{여기}\psi _{m,n}(t)=2^{-m/2}\psi(2^{-m}t-n).}

father

V_{i}

V_{i}

i {

style V

_ {

i

} father

V_{i}

、 father wavelet

Wi는 주파수

영역 속성을 유지합니다.

이들로부터 시퀀스는

\displaystyle \{0\}\subset \dots \{1}\subset V_{0}\subset V_{-1}\subset V_{-2}\subset \dots \set L^{2}(\mathbb {R})}

는 L의 다중² 해상도 분석을 형성하고,

\dots ,W_{1},W_{0},W_{-1},\dots

서브스페이스는

\dots ,W_{1},W_{0},W_{-1},\dots

\dots ,W_{1},W_{0},W_{-1},\dots

W-1

W-1, W_{0}, W_

{0}, W_

{-1},

\

dots

}, 즉 W는_m 서브스페이스_m−1 내의 V의_m 직교 "차이"입니다.

V_{m}\oplus W_{m}=V_{m-1}.

샘플링 정리와 마찬가지로 샘플링 거리^m 2 이하의 공간_m V가 0~1/2 범위의^m-1 주파수 베이스밴드를 커버한다고 결론지을 수 있다.직교 보체로서 W는 밴드_m[1^m−1/2, 1/2^m]를 대략 커버합니다.

이러한 포함 및 직교 관계, $V_{0}\oplus W_{0}=V_{-1}$ V $V_{0}\oplus W_{0}=V_{-1}$ $V_{0}\oplus W_{0}=V_{-1}$ 0 $V_{0}\oplus W_{0}=V_{-1}$ - $V_{0}\oplus W_{0}=V_{-1}$ { $displaystyle V_{0}\oplus$ W_ ${-1$ = $V_{-$ 1}은 시퀀스 $h=\{h_{n}\}_{n\in \mathbb {Z} }$ $=$ { $h=\{h_{n}\}_{n\in \mathbb {Z} }$ n $h=\{h_{n}\}_{n\in \mathbb {Z} }$ } $h=\{h_{n}\}_{n\in \mathbb {Z} }$ $h=\{h_{n}\}_{n\in \mathbb {Z} }$ { $displaystyle$ h $\h_n} \mathbbb$ { n $}$ 의 존재를 따른다.신분을 만족시키다

\displaystyle g_{n}=\displayle \phi _{0,0},\phi _{-1,n}\rangle }

따라서

{\textstyle \phi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }g_{n}\phi (2t-n),}

(

{\textstyle \phi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }g_{n}\phi (2t-n),}

t )

{\textstyle \phi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }g_{n}\phi (2t-n),}

{\textstyle \phi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }g_{n}\phi (2t-n),}

n

{\textstyle \phi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }g_{n}\phi (2t-n),}

{\textstyle \phi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }g_{n}\phi (2t-n),}

g

{\textstyle \phi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }g_{n}\phi (2t-n),}

(

{\textstyle \phi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }g_{n}\phi (2t-n),}

2 t

{\textstyle \phi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }g_{n}\phi (2t-n),}

-

{\textstyle \phi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }g_{n}\phi (2t-n),}

)

{\textstyle \phi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }g_{n}\phi (2t-n),}

, {

textstyle \phi

( t ) =

sq rt

{2}

\sum _

{n\in

\mathbbb

{Z} }g_{n} \phi

( 2

{\textstyle \phi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }g_{n}\phi (2t-n),}

-

{\textstyle \phi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }g_{n}\phi (2t-n),}

n ) , 。

h_{n}=\displayle \psi _{0,0},\phi _{-1,n}\rangle

(

{\textstyle \psi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }h_{n}\phi (2t-n).}

{\textstyle \psi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }h_{n}\phi (2t-n).}

{\textstyle \psi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }h_{n}\phi (2t-n).}

n

{\textstyle \psi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }h_{n}\phi (2t-n).}

Z

{\textstyle \psi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }h_{n}\phi (2t-n).}

n

{\textstyle \psi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }h_{n}\phi (2t-n).}

(

{\textstyle \psi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }h_{n}\phi (2t-n).}

t -

{\textstyle \psi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }h_{n}\phi (2t-n).}

) .

{\textstyle \psi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }h_{n}\phi (2t-n).}

{

textstyle \psi

( t ) =

sq

rt

{2}}

\

sum

_ {

n\in \mathbb {Z} }h_{n}\phi (2t-n)

가 되도록 합니다.} 첫

{\textstyle \psi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }h_{n}\phi (2t-n).}

번째 쌍의 두 번째 항등식은 아버지 웨이브릿 θ의 정제 방정식이다

.

두 아이덴티티 쌍은 모두 고속 웨이브릿 변환 알고리즘의 기초를 형성합니다.

다중 분해능 분석으로부터 공간² L의 직교 분해를 도출한다.

L^{2}=V_{j_{0}\oplus W_{j_{0}-1}\oplus W_{j_{0}-2}\oplus W_{j_{0}-3}\oplus \cdots

모든 신호 또는

S\in L^{2}

S

S\in L^{2}

L

S\in L^{2}

2 {\

displaystyle S\in L^{

2}}에

S\in L^2

대해 이는 해당하는 하위 공간의 기본 함수에서 다음과 같이 표현합니다.

\displaystyle S=\sum _{k}c_{j_{0},k}\phi _{j_{0}+\sum _{j\leq j_{0}}\sum _{k}d_{j,k}\psi _{j,k}

여기서 계수는

{\displaystyle c_{j_{0},k}=\phi S,\phi _{j_{0},k}\rangle

그리고.

displaystyle d_{j,k}=\si_{j,k}\rangle .}

실용적이고 효율적인 이유로, 마더(프로토타입) 웨이브릿(기능)으로서 콤팩트한 서포트를 가지는 연속적으로 구별 가능한 기능을 선호합니다.단, 해석요건(연속 WT)과 일반적으로 이론상의 이유로 $L^{1}(\mathbb {R} )\cap L^{2}(\mathbb {R} ).$ ( $L^{1}(\mathbb {R} )\cap L^{2}(\mathbb {R} ).$ $L^{1}(\mathbb {R} )\cap L^{2}(\mathbb {R} ).$ 의 부분공간에서 웨이브릿 함수를 선택합니다 $.\displaystyle$ L $^{1}(\mathbb {R})\cap$ L $^{2$ }(\ $mathbb {R})$ Lbes는 $L^1(\R)\cap L^2(\R).$ 다음과 같습니다.y 통합 가능 및 정사각형 통합 가능

\displaystyle \int _{-\infty }^{\infty } \psi (t) \,dt <\infty }

그리고.

\displaystyle \int _{-\infty }^{\infty } \psi (t)^{2},dt <\infty .}

이 공간에 있으면 평균 0과 표준 제곱 1의 조건을 공식화할 수 있습니다.

\displaystyle \int _{-\infty }^{\infty }\psi(t),dt=0}

0 평균의 조건입니다.

\displaystyle \int _{-\infty }^{\infty } \psi (t)^{2},dt=1}

제곱 노름 1의 조건입니다.

δ가 연속 웨이브릿 변환용 웨이브릿이 되기 위해서는(정확한 문장은 여기를 참조), 안정적으로 반전 가능한 변환을 얻기 위해서는 모 웨이브릿이 허용성 기준(완전하게 말하면 반미분성의 일종)을 충족해야 한다.

이산 웨이브 렛 변환에서는 적어도 웨이브 렛 계열이² 공간 L(R)에서의 동일성의 표현이라는 조건이 필요하다.이산 WT의 대부분의 구성에서는 스케일링 함수로 웨이브릿을 정의하는 다중 해상도 분석을 사용합니다.이 스케일링 함수 자체는 함수 방정식의 해법입니다.

대부분의 상황에서는 θ가 소실 모멘트의 M이 더 많은 연속 함수, 즉 모든 정수 m < M으로 제한하면 유용합니다.

displaystyle \int _{-\infty}^{\infty}t^{m},\psi(t),dt=0.}

모 웨이브릿은 a의 배수로 스케일링(또는 확장)되고 b의 배수로 변환(또는 이동)되어 다음과 같이 된다(모렛의 최초 공식에 따라).

(\displaystyle \psi _{a,b}(t)={1 \over {brt {a}\psi \leftsvt-b \over a}\right).}

연속 WT의 경우 쌍(a, b)은 전체 반평면₊ R × R에 걸쳐 변화하며, 이산 WT의 경우 이 쌍은 아핀 그룹이라고도 하는 그것의 이산 서브셋에 걸쳐 변화한다.

이러한 함수는 종종 (연속) 변환의 기본 함수로 잘못 언급됩니다.사실 연속 푸리에 변환과 마찬가지로 연속 웨이브릿 변환에는 기초가 없습니다.시간 빈도 해석에서는 (델프라트 이후) 미묘하게 다른 공식을 사용합니다.

: 약약항 :

${\frac {1}{\sqrt {a}}}\int _{-\infty }^{\infty }\varphi _{a1,b1}(t)\varphi \left({\frac {t-b}{a}}\right)\,dt$ a ${\frac {1}{\sqrt {a}}}\int _{-\infty }^{\infty }\varphi _{a1,b1}(t)\varphi \left({\frac {t-b}{a}}\right)\,dt$ - ${\frac {1}{\sqrt {a}}}\int _{-\infty }^{\infty }\varphi _{a1,b1}(t)\varphi \left({\frac {t-b}{a}}\right)\,dt$ - ∞ ${\frac {1}{\sqrt {a}}}\int _{-\infty }^{\infty }\varphi _{a1,b1}(t)\varphi \left({\frac {t-b}{a}}\right)\,dt$ , ${\frac {1}{\sqrt {a}}}\int _{-\infty }^{\infty }\varphi _{a1,b1}(t)\varphi \left({\frac {t-b}{a}}\right)\,dt$ ( ${\frac {1}{\sqrt {a}}}\int _{-\infty }^{\infty }\varphi _{a1,b1}(t)\varphi \left({\frac {t-b}{a}}\right)\,dt$ ) ${\frac {1}{\sqrt {a}}}\int _{-\infty }^{\infty }\varphi _{a1,b1}(t)\varphi \left({\frac {t-b}{a}}\right)\,dt$ ${\frac {1}{\sqrt {a}}}\int _{-\infty }^{\infty }\varphi _{a1,b1}(t)\varphi \left({\frac {t-b}{a}}\right)\,dt$ - ${\frac {1}{\sqrt {a}}}\int _{-\infty }^{\infty }\varphi _{a1,b1}(t)\varphi \left({\frac {t-b}{a}}\right)\,dt$ $）$ d ${\frac {1}{\sqrt {a}}}\int _{-\infty }^{\infty }\varphi _{a1,b1}(t)\varphi \left({\frac {t-b}{a}}\right)\,dt$ t { $display$ \ $style$ \ $frac {$ }{ - \ $infty }^{$ \ $infty$ } \ $varphi$ _ { $a$ , $b1}$ ( $t$ ) \ $varphi \ fract$ { d $}$ } $right$ { d } { d } right } $right$ }
$\Psi (t)$ ( $t$ ) { $displaystyle \Psi$ ( t ) 에는 시간 간격이 한정되어 $\Psi (t)$ .

푸리에 변환과의 비교(연속 시간)

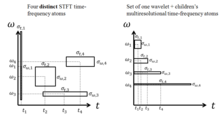
웨이브릿 변환은 종종 신호가 사인파의 합으로 표시되는 푸리에 변환과 비교됩니다.실제로 푸리에 변환은 모 웨이브릿 $\psi (t)=e^{-2\pi it}$ ( $\psi (t)=e^{-2\pi it}$ ) $\psi (t)=e^{-2\pi it}$ - $\psi (t)=e^{-2\pi it}$ $\psi (t)=e^{-2\pi it}$ i $\psi (t)=e^{-2\pi it}$ t \ $displaystyle \psi$ ( t) = $e^{-2\pi$ it $\psi (t)=e^{-2\pi it}$ 의 선택으로 연속 웨이브릿 변환의 특별한 경우로 볼 수 있다.일반적인 주요 차이점은 웨이브릿은 시간과 주파수 모두에서 국부화되지만 표준 푸리에 변환은 주파수에서만 국부화된다는 것입니다.Short-time Fourier Transform(STFT; 단시간 푸리에 변환)은 시간과 주파수가 국소화되어 있다는 점에서 웨이브릿 변환과 유사하지만 주파수/시간 분해능 트레이드오프에 문제가 있습니다.

창 커널을 할 수 .

itdisplaystyle \psi(t)=g(t-u)e^{-2\pi it}

g(t-u)

서

g(t-u)

g

g(t-u)

t

g(t-u)

-

g(t-u)

){

displaystyle

g (

{\textstyle \operatorname {rect} \left({\frac {t-u}{\Delta _{t}}}\right)}

-

{\textstyle \operatorname {rect} \left({\frac {t-u}{\Delta _{t}}}\right)}

g(t-u)

){

textstyle

\Delta _{t}

\

operatorname {rect

\

left

( { \

frac

{

{\textstyle \operatorname {rect} \left({\frac {t-u}{\Delta _{t}}}\right)}

t - u } { \

Delta _

{

t}

} \

right

}

{\textstyle \operatorname {rect} \left({\frac {t-u}{\Delta _{t}}}\right)}

} ,

\Delta _{t}

{\textstyle \operatorname {rect} \left({\frac {t-u}{\Delta _{t}}}\right)}

rect

\Delta _{t}

rect rect rect rect rect

rect

rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect rect as as파스발의 정리를 사용하여 웨이브렛의 에너지를 다음과 같이 정의할 수 있다.

E= _ frac pi } {{-\infty } {^{infty } {\infty } {\int }

이로부터 시간 u에 의한 윈도우 오프셋의 시간적 지지대의 제곱은 다음과 같이 주어진다.

^{2 dt}{\displaystyle _{t}^{2}=tfrac {1}\int t-u ^{2} \psi (t)^{2d}

$\xi$ 에 작용하는 창문의 스펙트럼 지지 제곱 $†(\displaystyle\xi)$

_{\ E \opha displaystyle _{\Omega2}=black {1}{2\pi E}{{\xi})

시간 영역에 직사각형 창이 있는 곱셈은 주파수 영역에서 $\operatorname {sinc} (\Delta _{t}\omega )$ $\operatorname {sinc} (\Delta _{t}\omega )$ ( $\operatorname {sinc} (\Delta _{t}\omega )$ $\operatorname {sinc} (\Delta _{t}\omega )$ $\operatorname {sinc} (\Delta _{t}\omega )$ ) ( \ $displaystyle \operatorname {sinc$ } ( \ $Delta$ _ ${$ t} \ $\operatorname {sinc} (\Delta _{t}\omega )$ obega ) 함수를 $\operatorname {sinc} (\Delta _{t}\omega )$ 사용하는 컨볼루션에 해당하므로 짧은 시간 창 또는 로컬화된 시간 창에 대한 가짜 호출 아티팩트가 발생합니다.연속 시간 푸리에 변환의 경우 $\Delta _{t}\to \infty$ t $\Delta _{t}\to \infty$ δ {\ $displaystyle \Delta$ _ ${t}\to$ \ $infty}$ 이며 $\Delta _{t}\to \infty$ , 이 회전은 푸리에 공간의 델타 함수와 함께 이루어지며, 결과적으로 $x(t)$ x $(\display$ x $(t$ 의 $x(t)$ 한 푸리에 변환이 됩니다.윈도우 기능은 가우스와 같은 다른 필터일 수 있습니다.윈도우 기능의 선택은 실제 푸리에 변환에 대한 근사 오차에 영향을 미칩니다.

주어진 분해능 셀의 시간 대역폭 곱은 STFT에서 초과할 수 없습니다.모든 STFT 기준 요소는 모든 시간적 이동 또는 오프셋에 대해 균일한 스펙트럼 및 시간적 지원을 유지하며, 따라서 낮은 주파수와 높은 주파수에 대한 시간에 동일한 분해능을 달성한다.분해능은 순수하게 샘플링 폭에 의해 결정됩니다.

이와는 대조적으로, 웨이브릿 변환의 멀티레볼루션 특성은 웨이브릿 변환의 스케일링 특성에 의해 높은 주파수에 대해 짧은 시간 폭을 유지하면서 낮은 주파수에 대한 대규모 시간적 지원을 가능하게 한다.이 특성은 기존의 시간 빈도 분석을 시간 척도 ^[8]분석으로 확장합니다.

STFT 시간 주파수 원자(왼쪽) 및 DWT 시간 척도 원자(오른쪽).시간 주파수 원자는 STFT에 사용되는 4가지 기본 함수입니다(즉, 4가지 개별 푸리에 변환 필요).DWT의 시간 스케일 원자는 단일 변환 기준 세트를 사용하여 고주파에는 작은 시간적 폭, 저주파에는 좋은 시간적 폭을 달성한다.

이산 웨이브릿 변환은 고속 푸리에 변환의 경우 O(N log N)에 비해 O(N) 시간이 걸리므로 계산적으로 덜 복잡합니다.이러한 계산상의 이점은 변환에 내재된 것이 아니라 주파수 로그 분할의 선택을 반영하며, 이는 DFT(Discrete Fourier ^[9]Transform)와 동일한 기본 함수를 사용하는 FFT(Fast Fourier Transform)의 등간격 주파수 분할과는 대조적입니다.또한 이 복잡도는 필터 크기가 신호 크기와 관련이 없는 경우에만 적용된다는 점도 중요합니다.섀넌 웨이브릿과 같이 컴팩트한 지원이 없는 웨이브릿은 O(N²)를 필요로 합니다.(예를 들어 로그 푸리에 변환도 O(N) 복잡도로 존재하지만 원래 신호는 특정 유형의 신호에서만 로그로 샘플링해야 합니다.)^[10]

의

패밀리은 다양한할 수 .

필터

직교 웨이브릿은 스케일링 필터에 의해 완전히 정의됩니다. 즉 길이 2N과 합계 1의 저역 통과 유한 임펄스 응답(FIR) 필터입니다.쌍직교 웨이브릿에서는 별도의 분해 및 재구성 필터가 정의된다.

직교 웨이브릿을 사용한 분석의 경우 하이패스 필터는 로우패스의 직교 미러 필터로 계산되며 재구성 필터는 분해 필터의 시간 역방향입니다.

도베치와 심플릿 웨이브렛은 스케일링 필터로 정의할 수 있습니다.

웨이브렛은 시간영역에서 웨이브렛 함수 δ(t)(즉, 모 웨이브렛) 및 스케일링 함수 δ(t)(아버지 웨이브렛이라고도 함)에 의해 정의된다.

웨이브릿 함수는 사실상 밴드 패스 필터이며 각 레벨에 대해 대역폭의 반을 스케일링합니다.이로 인해 전체 스펙트럼을 커버하기 위해서는 무한대의 레벨이 요구된다는 문제가 발생합니다.스케일링 함수는 변환의 가장 낮은 레벨을 필터링하여 모든 스펙트럼이 포함되도록 합니다.상세한^[11] 것에 대하여는, 을 참조해 주세요.

콤팩트 지지 웨이브릿은 길이가 유한하다고 간주할 수 있으며 스케일링 필터 g에 상당한다.

마이어 웨이브릿은 스케일링 함수로 정의할 수 있습니다.

웨이브릿에는 웨이브릿 함수 δ(t)로서 시간 영역 표현만 있습니다.

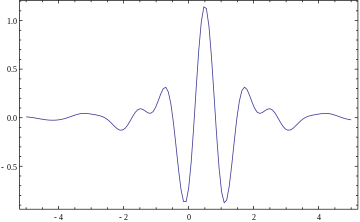
예를 들어 멕시코 해트 웨이브릿은 웨이브릿 함수로 정의할 수 있습니다.몇 가지 연속 웨이브릿 목록을 참조하십시오.

★★★

웨이브릿의 발달은 20세기 초 하르의 작품에서 시작하여 여러 개의 개별적인 사상열과 연관될 수 있다.이후 Dennis Gabor의 연구는 Gabor 원자(1946년)를 생산했는데, Gabor 원자는 웨이브렛과 유사하게 구성되어 유사한 목적에 적용되었다.

wavelet 이론에 그 이후로 주목할 만한 기여는 지속적인 작은 파도 변환(CWT)의 1975년(원래고 귀의 반응으로 들리기 위하여 공부하고 발견되는 달팽이관의 대해 변형을 불렀다)[12]피에르 Goupillaud, Grossmann 지금은 CWT(1982년), Jan-O으로 알려져 있Morlet의 배합에 츠바이크의 발견에 찾아볼 수 있다.lov이산 wavelets에 Strömberg의 초기 작품, 르 Gall–Tabatabai 선형 위상(1988년)[13][14][15]잉그리드 Daubechies의 직교 wavelets과 콤팩트 지원(1988년), Mallat의 비직교 multiresolution 체제(1989년), 알리 Akansu의 Binomial QMF(1990년), 나탈리 Delprat의 time-frequency에 5/3-taps 수직적 필터 뱅크(군수 수송)(1983년).terpretationAmir Said가 William A와 함께 개발한 계층형 트리의 집합 분할(SPIHT)에 대한 Newland의 조화 웨이브릿 변환(1993)과.1996년 ^[16]펄먼.

JPEG 2000 표준은 1997년부터 2000년까지 Touradj Ebrahimi(이후 JPEG 회장)^[17]가 의장을 맡은 JPEG(Joint Photographic Experts Group) 위원회에 의해 개발되었습니다.원래의 JPEG 형식에서 사용되는 DCT 알고리즘과 달리 JPEG 2000은 이산 웨이브릿 변환(DWT) 알고리즘을 사용합니다.손실 압축 알고리즘에는 CDF 9/7 웨이브릿 변환(1992년 Ingrid Daubechies에 의해 개발됨)을, 무손실 압축 ^[18]알고리즘에는 Le Gall-Tabatabai(LGT) 5/3 웨이브릿 변환(1988년 Didier Le Gall과 Ali J. Tabatabai에 의해 개발됨)을 사용한다.Motion JPEG 2000 확장을 포함한 JPEG 2000 기술은 ^[19]2004년 디지털 시네마의 비디오 코딩 표준으로 선정되었습니다.

★★★★★★★★★★★★

Alfréd Haar(1909)의 첫 번째 웨이브릿(Haar Wavelet)
1970년대 이후: George Zweig, Jean Morlet, Alex Grossmann
1980년대 이후 : 이브 마이어, 디디에 르갈, 알리 J. 타바타바이, 스테판 말라트, 잉그리드 도베치, 로널드 코이프만, 알리 아칸수, 빅터 위커하우저
1990년대 이후: Nathalie Delprat, Newland, Amir Said, William A.Pearlman, Touradj Ebrahimi, JPEG 2000

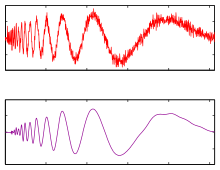
웨이브릿은 주어진 함수 또는 연속 시간 신호를 다른 스케일 성분으로 나누는 데 사용되는 수학 함수입니다.일반적으로 각 척도 성분에 주파수 범위를 할당할 수 있습니다.그런 다음 각 척도 성분을 척도와 일치하는 분해능으로 연구할 수 있습니다.웨이브릿 변환은 함수를 웨이브릿으로 표현한 것입니다.웨이브릿은 유한 길이 또는 빠르게 감소하는 진동 파형("마더 웨이브릿")의 스케일링 및 변환 복사본("딸 웨이브릿")입니다.웨이브릿 변환은 불연속성 및 날카로운 피크를 갖는 함수를 표현하고 유한, 비주기 및/또는 비정상 신호를 정확하게 분해 및 재구성하기 위한 기존의 푸리에 변환보다 장점이 있다.

웨이브릿 변환은 이산 웨이브릿 변환(DWT)과 연속 웨이브릿 변환(CWT)으로 분류됩니다.DWT와 CWT는 모두 연속시간(아날로그) 변환입니다.연속 시간(아날로그) 신호를 나타내는 데 사용할 수 있습니다.CWT는 가능한 모든 스케일 및 변환에 걸쳐 동작하지만 DWT는 스케일 및 변환 값 또는 표현 그리드의 특정 서브셋을 사용합니다.

각각 다른 애플리케이션에 적합한 다수의 웨이브릿 변환이 있습니다.전체 목록은 웨이브릿 관련 변환 목록을 참조하지만 일반적인 변환 목록은 다음과 같습니다.

연속 웨이브릿 변환(CWT)
이산 웨이브릿 변환(DWT)
고속 웨이브릿 변환(FWT)
리프팅 스킴 및 일반 리프팅 스킴
Wavelet 패킷 분해(WPD)
고정 웨이브릿 변환(SWT)
프랙셔널 푸리에 변환(FRFT)
프랙셔널 웨이브릿 변환(FRWT)

Transforms( 트랜스폼)

웨이브릿 변환이 특수한 경우인 일반화된 변환이 다수 있습니다.예를 들어, Yosef Joseph Segman은 하이젠베르크 그룹에 스케일을 도입하여 시간, 스케일 및 주파수의 함수인 연속 변환 공간을 만들었습니다.CWT는 결과 3d 시간 스케일 주파수 볼륨을 통과하는 2차원 슬라이스입니다.

일반화된 변환의 또 다른 예로는 CWT가 2차원 슬라이스인 채플릿 변환이 있습니다.

범용 변환의 중요한 응용 분야에는 고주파 분해능이 중요한 시스템이 포함됩니다.예를 들어, 직접 공간과 상호 공간 사이의 중간 다크필드 전자 광학 변환은 원자 군집의 조화 분석, 즉 결정 및 결정 ^[20]결함 연구에 널리 사용되어 왔다.이제 그 미션 전자 현미경 원자 주기성에picometer-scale 정보를 모든 종류의 nanostructure에서 디지털 영상을 보여 줄 수 있는, 높은 주파수 해상도( 같은 brushlets[24]과 ridgelets[25])과 패턴 recognition[21]와 중간 변환에 대하strain[22][23]애플리케이션의 범위는g.빠르게 노를 젓고.

프랙셔널 웨이브릿 변환(FRWT)은 프랙셔널 푸리에 변환 도메인에서의 고전적인 웨이브릿 변환의 일반화입니다.이 변환은 시간 영역 및 분수 영역 정보를 동시에 제공하고 시간-분할 주파수 ^[26]평면에 신호를 나타낼 수 있습니다.

프로그램

일반적으로 신호가 이미 샘플링된 경우 데이터 압축에는 DWT에 대한 근사치가 사용되며 신호 ^[27]분석에는 CWT가 사용됩니다.따라서 DWT 근사치는 공학 및 컴퓨터 과학에서 일반적으로 사용되며 CWT는 과학 연구에서 사용됩니다.

다른 변환과 마찬가지로 웨이브릿 변환을 사용하여 데이터를 변환한 다음 변환된 데이터를 인코딩하여 효과적인 압축을 수행할 수 있습니다.예를 들어 JPEG 2000은 쌍직교 웨이브렛을 사용하는 이미지 압축 표준입니다.즉, 프레임이 과완전하지만 꽉 끼는 프레임(벡터 공간의 프레임 유형 참조)이며, 분석과 합성 모두에 동일한 프레임 함수(복소 웨이브릿의 경우 결합 제외)가 사용된다. 즉, 정방향 변환과 역방향 변환 모두에서 사용된다.자세한 내용은 웨이브릿 압축을 참조하십시오.

이와 관련된 용도는 웨이브릿 수축이라고도 하는 웨이브릿 계수 임계값에 기초한 데이터의 평활/디노이즈에 사용됩니다.바람직하지 않은 주파수 성분에 대응하는 웨이브릿 계수를 적응적으로 임계값화함으로써 평활화 및/또는 노이즈 제거 연산을 실행할 수 있다.

웨이브릿 변환은 통신 애플리케이션에도 사용되기 시작하고 있습니다.Wavelet OFDM은 HD-PLC(Panasonic이 개발한 전력선 통신 기술) 및 IEEE 1901 표준에 포함된 옵션 모드 중 하나에 사용되는 기본 변조 방식입니다.Wavelet OFDM은 기존 FFT OFDM보다 더 깊은 노치를 달성할 수 있으며, Wavelet OFDM에는 가드 간격(일반적으로 FFT OFDM ^[28]시스템에서 상당한 오버헤드를 나타냄)이 필요하지 않습니다.

의

대부분의 경우 신호는 사인파의 합으로 잘 표현될 수 있습니다.그러나 갑작스러운 불연속성을 갖는 비연속 신호를 고려하십시오. 이 신호는 여전히 사인파의 합으로 표현될 수 있지만 무한수가 필요하며, 이는 깁스 현상이라고 알려진 관측치입니다.따라서 이 방법에는 무한대의 푸리에 계수가 필요하며 압축과 같은 많은 응용 프로그램에서는 실용적이지 않습니다.웨이브렛은 시간 현지화 동작(푸리에 변환과 웨이브렛 변환 모두 주파수 현지화되지만 웨이브렛에는 시간 현지화 특성이 추가됨) 때문에 불연속성을 갖는 신호를 설명하는 데 더 유용합니다.이 때문에 실제로 사용되는 많은 유형의 신호는 푸리에 도메인에서는 비희박하지만 웨이브릿 도메인에서는 매우 희박합니다.이는 신호 재구성, 특히 최근에 널리 사용되는 압축 감지 분야에서 특히 유용합니다.(단시간 푸리에 변환(STFT)은 시간과 주파수로도 국지화되지만 주파수-시간 분해능의 트레이드오프에 문제가 있는 경우가 많습니다).웨이브렛은 다중 해상도 분석으로 인해 더 나은 신호 표현입니다.)

이는 웨이브릿 변환이 현재 수많은 애플리케이션에 채택되고 있는 이유이며, 종종 기존의 푸리에 변환을 대체한다.분자역학, 카오스 이론,^[29] ab initio 계산, 천체물리학, 중력파 과도 데이터 분석,^[30]^[31] 밀도 매트릭스 국재화, 지진학, 광학, 난류 및 양자역학을 포함한 많은 물리학 분야들이 이러한 패러다임의 변화를 보아왔다.이러한 변화는 영상 처리, EEG,^[32] EMG, 심전도 분석, 뇌 리듬, DNA 분석, 단백질 분석, 기후학, 인간 성반응 분석,^[33] 일반 신호 처리, 음성 인식, 음향, ^[34]진동 신호, 컴퓨터 그래픽, 멀티프랙탈 분석, 희박 부호화에서도 일어났다.컴퓨터 비전과 화상 처리에서 스케일 공간 표현과 가우스 도함수 연산자의 개념은 표준 멀티 스케일 표현으로 간주된다.

제거

변환 에 의한 신호

노이즈 $x=s+v$ x $x=s+v$ + $x=s+v$ ${\displaystyle$ x $=s+v$ 를 측정한다고 가정합니다. 여기서 s는 신호를 나타내고 v는 노이즈를 나타냅니다.가 특정 웨이브릿 기준으로 희박한 표현을 $v\ \sim \ {\mathcal {N}}(0,\,\sigma ^{2}I)$ v $v\ \sim \ {\mathcal {N}}(0,\,\sigma ^{2}I)$ ~ $v\ \sim \ {\mathcal {N}}(0,\,\sigma ^{2}I)$ ( 0 $v\ \sim \ {\mathcal {N}}(0,\,\sigma ^{2}I)$ , $v\ \sim \ {\mathcal {N}}(0,\,\sigma ^{2}I)$ $v\ \sim \ {\mathcal {N}}(0,\,\sigma ^{2}I)$ I ) $v\ \sim \ {\mathcal {N}}(0,\,\sigma ^{2}I)$ { $display style$ v $\ sim$ \ { $N$ } （ $0$ , \ $sigma ^ {2$ } I $v\ \sim \ {\mathcal {N}}(0,\,\sigma ^{2}I)$ } } 。

$x의$ 웨이브릿 변환을 $y=W^{T}x=W^{T}s+W^{T}v=p+z$ $y=W^{T}x=W^{T}s+W^{T}v=p+z$ $y=W^{T}x=W^{T}s+W^{T}v=p+z$ $y=W^{T}x=W^{T}s+W^{T}v=p+z$ $y=W^{T}x=W^{T}s+W^{T}v=p+z$ $y=W^{T}x=W^{T}s+W^{T}v=p+z$ $y=W^{T}x=W^{T}s+W^{T}v=p+z$ $y=W^{T}x=W^{T}s+W^{T}v=p+z$ + $y=W^{T}x=W^{T}s+W^{T}v=p+z$ $y=W^{T}x=W^{T}s+W^{T}v=p+z$ v $y=W^{T}x=W^{T}s+W^{T}v=p+z$ p + z { $display$ $y=W^{T}x=W^{T}s+W^{T}v=p+z$ $= W$ = W = { T } x $y=W^{T}x=W^{T}s+W^{T}v=p+z$ = W = W { $T }$ s $y=W^{T}x=W^{T}s+W^{T}v=p+z$ + W $^{$ W } { $T}v=p+z$ $p=W^{T}s$ $p=W^{T}s$ $p=W^{T}s$ $p=W^{T}s$ s(\ $displaystyle$ p $=W^{T}s$ 신호 성분의 웨이브릿 변환. $z=W^{T}v$ $z=W^{T}v$ $z=W^{T}v$ $z=W^{T}v$ v \ $displaystyle$ z $=W^{$ $T}v$ 노이즈 성분의 웨이브릿 변환.

p의 대부분의 요소는 0 또는 0에 가깝습니다 $z\ \sim \ \ {\mathcal {N}}(0,\,\sigma ^{2}I)$ ~ $z\ \sim \ \ {\mathcal {N}}(0,\,\sigma ^{2}I)$ ( $z\ \sim \ \ {\mathcal {N}}(0,\,\sigma ^{2}I)$ , $z\ \sim \ \ {\mathcal {N}}(0,\,\sigma ^{2}I)$ $z\ \sim \ \ {\mathcal {N}}(0,\,\sigma ^{2}I)$ I $z\ \sim \ \ {\mathcal {N}}(0,\,\sigma ^{2}I)$ ) { $displaystyle z$ \ $sim \$ \ \ $mathcal$ { $N$ } （ $0$ , , , \ $sigma$ ^ {2 $}$ $I$ } }

W는 직교이므로 추정 문제는 iid 가우스 노이즈의 신호 회복에 해당합니다.p는 희박하기 때문에 한 가지 방법은 p에 대해 가우스 혼합 모델을 적용하는 것입니다.

$p\ \sim \ a{\mathcal {N}}(0,\,\sigma _{1}^{2})+(1-a){\mathcal {N}}(0,\,\sigma _{2}^{2})$ p $p\ \sim \ a{\mathcal {N}}(0,\,\sigma _{1}^{2})+(1-a){\mathcal {N}}(0,\,\sigma _{2}^{2})$ ~ $p\ \sim \ a{\mathcal {N}}(0,\,\sigma _{1}^{2})+(1-a){\mathcal {N}}(0,\,\sigma _{2}^{2})$ $p\ \sim \ a{\mathcal {N}}(0,\,\sigma _{1}^{2})+(1-a){\mathcal {N}}(0,\,\sigma _{2}^{2})$ ( 0 $p\ \sim \ a{\mathcal {N}}(0,\,\sigma _{1}^{2})+(1-a){\mathcal {N}}(0,\,\sigma _{2}^{2})$ , $p\ \sim \ a{\mathcal {N}}(0,\,\sigma _{1}^{2})+(1-a){\mathcal {N}}(0,\,\sigma _{2}^{2})$ 1 $p\ \sim \ a{\mathcal {N}}(0,\,\sigma _{1}^{2})+(1-a){\mathcal {N}}(0,\,\sigma _{2}^{2})$ ) $p\ \sim \ a{\mathcal {N}}(0,\,\sigma _{1}^{2})+(1-a){\mathcal {N}}(0,\,\sigma _{2}^{2})$ + ( $p\ \sim \ a{\mathcal {N}}(0,\,\sigma _{1}^{2})+(1-a){\mathcal {N}}(0,\,\sigma _{2}^{2})$ - $p\ \sim \ a{\mathcal {N}}(0,\,\sigma _{1}^{2})+(1-a){\mathcal {N}}(0,\,\sigma _{2}^{2})$ ) $p\ \sim \ a{\mathcal {N}}(0,\,\sigma _{1}^{2})+(1-a){\mathcal {N}}(0,\,\sigma _{2}^{2})$ ( $p\ \sim \ a{\mathcal {N}}(0,\,\sigma _{1}^{2})+(1-a){\mathcal {N}}(0,\,\sigma _{2}^{2})$ , $p\ \sim \ a{\mathcal {N}}(0,\,\sigma _{1}^{2})+(1-a){\mathcal {N}}(0,\,\sigma _{2}^{2})$ 2 $){$ $displaystyle$ p $\ sim$ \ $a$ { \ $mathcal$ { $N$ } ( 0 , , \ $sigma _$ { { $1$ } )+ ( 1 - $a$ ) { \ $mathcal$ { $N$ } ( $0$ , 0 , \ sigmigma ) } ( 0 , \ $sigma$ ) { { { { { { { { { { $2$ } } $p\ \sim \ a{\mathcal {N}}(0,\,\sigma _{1}^{2})+(1-a){\mathcal {N}}(0,\,\sigma _{2}^{2})$ } ) } { { $\sigma _{1}^{2}$ } } { { { { { { 2 $\sigma _{1}^{2}$ } } } } $}^{$ 2 $\sigma _{2}^{2}$ }}은 "미미한" 계수의 분산입니다.

${\tilde {p}}=E(p/y)=\tau (y)y$ ~ ${\tilde {p}}=E(p/y)=\tau (y)y$ ${\tilde {p}}=E(p/y)=\tau (y)y$ ( ${\tilde {p}}=E(p/y)=\tau (y)y$ / ${\tilde {p}}=E(p/y)=\tau (y)y$ ) ${\tilde {p}}=E(p/y)=\tau (y)y$ ${\tilde {p}}=E(p/y)=\tau (y)y$ ( $y$ ) ${\tilde {p}}=E(p/y)=\tau (y)y$ ( \ $displaystyle$ { $p$ } $= E$ ( $p$ / y ) $=$ \ $tau ($ $y$ ) ${\tilde {p}}=E(p/y)=\tau (y)y$ 、 $\tau (y)$ $）$ $\tau (y)$ display 、 \ $displaystyle$ $\tau (y)$ \ $tau$ ( y ) display $\tau (y)$ 、 display display display $\sigma _{1}^{2}$ $\sigma _{1}^{2}$ $display2$ $\sigma _{1}^{2}$ display2 $\sigma _{2}^{2}$ display2 display2 display2 display2 display2 display2 $\sigma _{1}^{2}$ display2 display2 display2 display2 display2 display2 display2 $\sigma _{2}^{2}$ display2 display2 역변환을 적용하면 희소성 가정으로 인해 예상된 소량의 신호가 손실됩니다.큰 계수는 주로 희소성으로 인한 신호를 나타낼 것으로 예상되며, 통계적으로 노이즈의 대부분이지만 매우 적은 수의 신호만이 이러한 낮은 크기 계수로 표시될 것으로 예상됩니다.따라서 영점 조정 동작은 노이즈의 대부분을 제거하며 신호는 많지 않을 것으로 예상됩니다.일반적으로 위의 임계값 계수는 이 공정 중에 수정되지 않습니다.웨이브릿 기반 노이즈 제거를 위한 일부 알고리즘은 그러한 감쇠에 의해 제거될 것으로 예상되는 소음의 양에 대한 통계적 추정치에 기초하여 더 큰 계수를 감쇠시킬 수도 있다.

마지막으로 역웨이브릿 변환을 적용하여 ${\tilde {s}}=W{\tilde {p}}$ ~ ${\tilde {s}}=W{\tilde {p}}$ ${\tilde {s}}=W{\tilde {p}}$ ~ {\ $displaystyle {s} =$ $W{\tilde {p}}}$

멀티스케일 기후 네트워크

Agarwal 등에서는 기후를 다양한 타임스케일로 복잡한 네트워크로 구축하고 조사하기 위해 웨이브릿 기반의 고급 선형 및 비선형 방법을 제안했다.다양한 타임스케일의 SST 데이터 세트를 사용하여 구축된 기후 네트워크는 웨이브릿 기반의 기후 프로세스 멀티스케일 분석이 프로세스가 한 타임스케일로 분석될 때 놓칠 수 있는 시스템 역학을 더 잘 이해할 수 있는 가능성을 가지고 있다.

웨이브릿 목록

이산 웨이브릿

베일킨(18)
무어 웨이브릿
BNC 웨이브릿(biorthogonal nearly coiflet) 웨이브릿
코이플렛(6, 12, 18, 24, 30)
Cohen-Daubechies-Fauveau 웨이브렛(CDF N/P 또는 Daubechies 바이오직교 웨이브렛이라고도 함)
도베키 웨이브릿 (2, 4, 6, 8, 10, 12, 14, 16, 18, 20 등)
이항-QMF(Daubechies 웨이브릿이라고도 함)
하르 웨이브릿
마티외 웨이브릿
레전드르 웨이브릿
빌라세노르 웨이브릿
심플릿^[38]

연속 웨이브릿

실수치

복소수치

「」를 참조해 주세요.

차플렛 변환
커브릿
디지털 시네마
필터 뱅크
프랙탈 압축
분수 푸리에 변환
JPEG 2000
불규칙한 간격을 포함한 모든 데이터에서 주기성을 계산하기 위한 최소 제곱 스펙트럼 분석
다중 해상도 분석
노이즈릿
비분리 웨이브릿
공간 축척
스케일 상관
시어릿
단시간 푸리에 변환
초광대역 무선 송신 웨이브릿
웨이브 패킷
Gabor wavelet #웨이브릿 공간^[39]
치수 축소
푸리에 관련 변환
스펙트로그램
Huygens-Fresnel 원리(물리 웨이브릿)

레퍼런스

^ 무선통신: 원칙과 실천, 프렌티스홀 통신엔지니어링과 신흥테크놀로지 시리즈, T. S. Rapport, 프렌티스홀, 2002년 페이지 126
^ Ricker, Norman (1953). "Wavelet Contraction, Wavelet Expansion, and the Control of Seismic Resolution". Geophysics. 18 (4): 769–792. Bibcode:1953Geop...18..769R. doi:10.1190/1.1437927.
^ Meyer, Yves(1992), Wavelets and Operators, 영국, 캠브리지 대학 출판부, ISBN 0-521-42000-8
^ Chui, Charles K.(1992), 샌디에이고 웨이브릿 소개, CA: 학술 출판사, ISBN 0-12-174584-8
^ 도깨비들, 잉그리드.(1992), 웨이브렛 10강좌, SIAM, ISBN 978-0-89871-274-2
^ Akansu, Ali N.; Haddad, Richard A.(1992), 다중 해상도 신호 분해:트랜스폼, 서브밴드, 웨이브릿, 보스턴, 매사추세츠: Academic Press, ISBN 978-0-12-047141-6
^ Larson, David R. (2007). "Wavelet Analysis and Applications (See: Unitary systems and wavelet sets)". Appl. Numer. Harmon. Anal. Birkhäuser: 143–171. {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)
^ 말라트, 스테판"신호 처리 웨이브릿 투어, 1998" 250-252
^ 스티븐 W. 스미스의 디지털 신호 처리에 대한 과학자와 엔지니어 가이드, 박사 8장 방정식 8-1: http://www.dspguide.com/ch8/4.htm
^ Haines, VG. V.; Jones, Alan G. (1988). "Logarithmic Fourier Transform" (PDF). Geophysical Journal (92): 171–178. doi:10.1111/j.1365-246X.1988.tb01131.x.
^ "A Really Friendly Guide To Wavelets – PolyValens". www.polyvalens.com.
^ Weisstein, Eric W. "Zweig, George -- from Eric Weisstein's World of Scientific Biography". scienceworld.wolfram.com. Retrieved 2021-10-20.
^ Sullivan, Gary (8–12 December 2003). "General characteristics and design considerations for temporal subband video coding". ITU-T. Video Coding Experts Group. Retrieved 13 September 2019.
^ Bovik, Alan C. (2009). The Essential Guide to Video Processing. Academic Press. p. 355. ISBN 9780080922508.
^ Gall, Didier Le; Tabatabai, Ali J. (1988). "Sub-band coding of digital images using symmetric short kernel filters and arithmetic coding techniques". ICASSP-88., International Conference on Acoustics, Speech, and Signal Processing: 761–764 vol.2. doi:10.1109/ICASSP.1988.196696. S2CID 109186495.
^ Said, Amir; Pearlman, William A. (June 1996). "A new fast and efficient image codec based on set partitioning in hierarchical trees". IEEE Transactions on Circuits and Systems for Video Technology. 6 (3): 243–250. doi:10.1109/76.499834. ISSN 1051-8215.
^ Taubman, David; Marcellin, Michael (2012). JPEG2000 Image Compression Fundamentals, Standards and Practice: Image Compression Fundamentals, Standards and Practice. Springer Science & Business Media. ISBN 9781461507994.
^ Unser, M.; Blu, T. (2003). "Mathematical properties of the JPEG2000 wavelet filters" (PDF). IEEE Transactions on Image Processing. 12 (9): 1080–1090. Bibcode:2003ITIP...12.1080U. doi:10.1109/TIP.2003.812329. PMID 18237979. S2CID 2765169. Archived from the original (PDF) on 2019-10-13.
^ Swartz, Charles S. (2005). Understanding Digital Cinema: A Professional Handbook. Taylor & Francis. p. 147. ISBN 9780240806174.
^ P. 허쉬, A.Howie, R.Nicholson, D. W. Pashley 및 M. J. Wheelan(1965/1977) 박결정 전자현미경(Butterworths, London/Krieger, Malabar FLA) ISBN 0-88275-376-2
^ P. 프라운도르프, J. 왕, E. 만델, M.Rose (2006) 디지털 다크필드 표, 현미경 및 마이크로 분석 12:S2, 1010–1011 (cf. arXiv: cond-mat/0403017)
^ Hÿtch, M. J.; Snoeck, E.; Kilaas, R. (1998). "Quantitative measurement of displacement and strain fields from HRTEM micrographs". Ultramicroscopy. 74 (3): 131–146. doi:10.1016/s0304-3991(98)00035-7.
^ Martin Rose(2006) 디지털 다크필드 분해를 사용한 HRTEM 영상의 격자 테두리 간격 측정(미국 미주리주(州) - 세인트루이스주)루이스)
^ F. G. Meyer와 R. R. Coifman(1997) 응용 및 계산 고조파 분석 4:147.
^ A. G. Flesia, H. Hel-Or, A.Averbucch, E. J. Candes, R. R. Coifman 및 D. L. Donoho (2001) 리지렛 패킷의 디지털 실장(Academical Press, New York).
^ Shi, J.; Zhang, N.-T.; Liu, X.-P. (2011). "A novel fractional wavelet transform and its applications". Sci. China Inf. Sci. 55 (6): 1270–1279. doi:10.1007/s11432-011-4320-x.
^ A.N. Akansu, W.A. Serdijn 및 I.W. Selesnick, 웨이브릿의 새로운 응용 프로그램: 리뷰, 물리 커뮤니케이션, 엘세비어, 제3호, 제1, 페이지 1-18, 2010년 3월.
^ Stefano Galli; O. Logvinov (July 2008). "Recent Developments in the Standardization of Power Line Communications within the IEEE". IEEE Communications Magazine. 46 (7): 64–71. doi:10.1109/MCOM.2008.4557044. S2CID 2650873. P1901 PHY/MAC 제안 개요
^ Wotherspoon, T.; et., al. (2009). "Adaptation to the edge of chaos with random-wavelet feedback". J. Phys. Chem. 113 (1): 19–22. Bibcode:2009JPCA..113...19W. doi:10.1021/jp804420g. PMID 19072712.
^ Abbott, Benjamin P.; et al. (LIGO Scientific Collaboration and Virgo Collaboration) (2016). "Observing gravitational-wave transient GW150914 with minimal assumptions". Phys. Rev. D. 93 (12): 122004. arXiv:1602.03843. Bibcode:2016PhRvD..93l2004A. doi:10.1103/PhysRevD.93.122004. S2CID 119313566.
^ V Necula, S Klimenko and G Mitselmakher (2012). "Transient analysis with fast Wilson-Daubechies time-frequency transform". Journal of Physics: Conference Series. 363 (1): 012032. Bibcode:2012JPhCS.363a2032N. doi:10.1088/1742-6596/363/1/012032.
^ J. 라피 외보철물을 위한 전완 EMG 신호의 기능 추출, Expert Systems with Applications 38 (2011) 4058–67.
^ J. 라피 외신호 처리 기술을 사용한 여성 성반응, Journal of Sexual Medicine 6 (2009) 3086–96. (pdf)
^ Rafiee, J.; Tse, Peter W. (2009). "Use of autocorrelation in wavelet coefficients for fault diagnosis". Mechanical Systems and Signal Processing. 23 (5): 1554–72. Bibcode:2009MSSP...23.1554R. doi:10.1016/j.ymssp.2009.02.008.
^ Agarwal, Ankit; Maheswaran, Rathinasamy; Marwan, Norbert; Caesar, Levke; Kurths, Jürgen (November 2018). "Wavelet-based multiscale similarity measure for complex networks" (PDF). The European Physical Journal B. 91 (11): 296. Bibcode:2018EPJB...91..296A. doi:10.1140/epjb/e2018-90460-6. eISSN 1434-6036. ISSN 1434-6028. S2CID 125557123.
^ Agarwal, Ankit; Marwan, Norbert; Rathinasamy, Maheswaran; Merz, Bruno; Kurths, Jürgen (13 October 2017). "Multi-scale event synchronization analysis for unravelling climate processes: a wavelet-based approach". Nonlinear Processes in Geophysics. 24 (4): 599–611. Bibcode:2017NPGeo..24..599A. doi:10.5194/npg-24-599-2017. eISSN 1607-7946.
^ Agarwal, Ankit; Caesar, Levke; Marwan, Norbert; Maheswaran, Rathinasamy; Merz, Bruno; Kurths, Jürgen (19 June 2019). "Network-based identification and characterization of teleconnections on different scales". Scientific Reports. 9 (1): 8808. Bibcode:2019NatSR...9.8808A. doi:10.1038/s41598-019-45423-5. eISSN 2045-2322. PMC 6584743. PMID 31217490.
^ Matlab Toolbox – URL : http://matlab.izmiran.ru/help/toolbox/wavelet/ch06_a32.html
^ Erik Hjelmoss (1999-01-21) Gabor Wavelets URL : http://www.ansatt.hig.no/erikh/papers/scia99/node6.html

추가 정보

Haar A., Zur Theory der Orthogonalen Funktionensysteme, Mathathische Annalen, 69, 페이지 331–371, 1910.
Ingrid Daubechies, Wavelet에 관한 10가지 강의, 산업 및 응용 수학 학회, 1992년, ISBN 0-89871-274-2
Ali Akansu와 Richard Haddad, 다중 해상도 신호 분해: 트랜스폼, 서브밴드, Wavelets, Academic Press, 1992, ISBN 0-12-047140-X
P. P. Vaidyanathan, 프렌티스 홀, 멀티레이트 시스템과 필터 뱅크, 1993, ISBN 0-13-605718-7
Gerald Kaiser, Wavelets 프렌들리 가이드, Birkhauser, 1994, ISBN 0-8176-3711-7
Mladen Victor Wickerhauser, 이론에서 소프트웨어로의 적응 웨이브릿 분석, A Peters Ltd, 1994, ISBN 1-56881-041-5
마르틴 베테를리와 옐레나 코바체비치, "웨이브릿과 서브밴드 코딩", 프렌티스 홀, 1995, ISBN 0-13-097080-8
바바라 버크 허바드, "웨이블렛에 따른 세계:「만드는 수학 기술 이야기」, 1998년, ISBN 1-56881-072-5, ISBN 978-1-56881-072-0
Stéphane Mallat, "신호처리의 웨이브릿 투어" 제2판, 아카데미 프레스, 1999, ISBN 0-12-466606-X
도날드Percival 및 Andrew T. Walden, Wavelet Methods for Time Series Analysis, Cambridge University Press, 2000, ISBN 0-521-68508-7
Ramazan Genchay, Faruk Selchuk and Brandon Whitcher, An Instruction to Wavelets and Other Filtering Methods in Finance and Economics, 2001, ISBN 0-12-279670-5
Paul S. Addison, The Illustrated Wavelet Transform Handbook, 물리연구소, 2002, ISBN 0-7503-0692-0
B. Boash 편집자, "시간 주파수 신호 분석 및 처리 – 포괄적인 참조", Elsevier Science, Oxford, 2003, ISBN 0-08-044335-4.
Tony F. Chan 및 "Jackie (Jianhong)" Shen, 이미지 처리 및 분석 – 변분법, PDE, 웨이브릿 및 확률적 방법, 응용수학회, ISBN 0-89871-589-X (2005)
Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Section 13.10. Wavelet Transforms", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
^[1]

외부 링크

"Wavelet analysis", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
웨이브렛에 관한 제1회 NJIT 심포지엄(1990년 4월 30일) (미국 제1회 웨이브렛 회의)
이항 QMF 도베키 웨이브릿
길버트 스트랭의 웨이브릿, American Scientist 82(1994) 250~255. (매우 짧고 훌륭한 소개)
UC Santa Barbara에서 웨이브렛에 관한 강좌,
Wavelet for Kids (PDF 파일) (개론 (매우 똑똑한 어린이용!))
WITS: 별자리는 어디 있어?-let으로 끝나는 수십 개의 웨이브릿 및 웨이브릿 관련 용어로 구성된 사전. -let에서 밴들렛, 윤곽선, 곡선, 노이즈렛, 웨지렛을 통해 -let으로 끝납니다.
프랙셔널 스플라인 웨이브릿 변환은 프랙셔널 b-스플라인을 기반으로 한 프랙셔널 웨이브릿 변환을 나타냅니다.
멀티스케일 기하학적 표현, 공간적, 방향성 및 주파수 선택성의 파노라마는 2차원 지향 웨이브릿 및 관련 기하학적 멀티스케일 변환에 대한 튜토리얼을 제공합니다.
René Puschinger의 웨이브렛 개요
"How Wavelets Allow Researchers to Transform — and Understand — Data". Quanta Magazine. 2021-10-13. Retrieved 2021-10-20.

^ "How Wavelets Allow Researchers to Transform — and Understand — Data". Quanta Magazine. 2021-10-13. Retrieved 2021-10-20.

[1] 무선통신: 원칙과 실천, 프렌티스홀 통신엔지니어링과 신흥테크놀로지 시리즈, T. S. Rapport, 프렌티스홀, 2002년 페이지 126

[2] Ricker, Norman (1953). "Wavelet Contraction, Wavelet Expansion, and the Control of Seismic Resolution". Geophysics. 18 (4): 769–792. Bibcode:1953Geop...18..769R. doi:10.1190/1.1437927.

[3] Meyer, Yves(1992), Wavelets and Operators, 영국, 캠브리지 대학 출판부, ISBN 0-521-42000-8

[4] Chui, Charles K.(1992), 샌디에이고 웨이브릿 소개, CA: 학술 출판사, ISBN 0-12-174584-8

[5] 도깨비들, 잉그리드.(1992), 웨이브렛 10강좌, SIAM, ISBN 978-0-89871-274-2

[6] Akansu, Ali N.; Haddad, Richard A.(1992), 다중 해상도 신호 분해:트랜스폼, 서브밴드, 웨이브릿, 보스턴, 매사추세츠: Academic Press, ISBN 978-0-12-047141-6

[7] Larson, David R. (2007). "Wavelet Analysis and Applications (See: Unitary systems and wavelet sets)". Appl. Numer. Harmon. Anal. Birkhäuser: 143–171. {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)

[8] 말라트, 스테판"신호 처리 웨이브릿 투어, 1998" 250-252

[9] 스티븐 W. 스미스의 디지털 신호 처리에 대한 과학자와 엔지니어 가이드, 박사 8장 방정식 8-1: http://www.dspguide.com/ch8/4.htm

[10] Haines, VG. V.; Jones, Alan G. (1988). "Logarithmic Fourier Transform" (PDF). Geophysical Journal (92): 171–178. doi:10.1111/j.1365-246X.1988.tb01131.x.

[11] "A Really Friendly Guide To Wavelets – PolyValens". www.polyvalens.com.

[12] Weisstein, Eric W. "Zweig, George -- from Eric Weisstein's World of Scientific Biography". scienceworld.wolfram.com. Retrieved 2021-10-20.

[13] Sullivan, Gary (8–12 December 2003). "General characteristics and design considerations for temporal subband video coding". ITU-T. Video Coding Experts Group. Retrieved 13 September 2019.

[14] Bovik, Alan C. (2009). The Essential Guide to Video Processing. Academic Press. p. 355. ISBN 9780080922508.

[15] Gall, Didier Le; Tabatabai, Ali J. (1988). "Sub-band coding of digital images using symmetric short kernel filters and arithmetic coding techniques". ICASSP-88., International Conference on Acoustics, Speech, and Signal Processing: 761–764 vol.2. doi:10.1109/ICASSP.1988.196696. S2CID 109186495.

[Said-16] Said, Amir; Pearlman, William A. (June 1996). "A new fast and efficient image codec based on set partitioning in hierarchical trees". IEEE Transactions on Circuits and Systems for Video Technology. 6 (3): 243–250. doi:10.1109/76.499834. ISSN 1051-8215.

[17] Taubman, David; Marcellin, Michael (2012). JPEG2000 Image Compression Fundamentals, Standards and Practice: Image Compression Fundamentals, Standards and Practice. Springer Science & Business Media. ISBN 9781461507994.

[Unser-18] Unser, M.; Blu, T. (2003). "Mathematical properties of the JPEG2000 wavelet filters" (PDF). IEEE Transactions on Image Processing. 12 (9): 1080–1090. Bibcode:2003ITIP...12.1080U. doi:10.1109/TIP.2003.812329. PMID 18237979. S2CID 2765169. Archived from the original (PDF) on 2019-10-13.

[19] Swartz, Charles S. (2005). Understanding Digital Cinema: A Professional Handbook. Taylor & Francis. p. 147. ISBN 9780240806174.

[20] P. 허쉬, A.Howie, R.Nicholson, D. W. Pashley 및 M. J. Wheelan(1965/1977) 박결정 전자현미경(Butterworths, London/Krieger, Malabar FLA) ISBN 0-88275-376-2

[21] P. 프라운도르프, J. 왕, E. 만델, M.Rose (2006) 디지털 다크필드 표, 현미경 및 마이크로 분석 12:S2, 1010–1011 (cf. arXiv: cond-mat/0403017)

[22] Hÿtch, M. J.; Snoeck, E.; Kilaas, R. (1998). "Quantitative measurement of displacement and strain fields from HRTEM micrographs". Ultramicroscopy. 74 (3): 131–146. doi:10.1016/s0304-3991(98)00035-7.

[23] Martin Rose(2006) 디지털 다크필드 분해를 사용한 HRTEM 영상의 격자 테두리 간격 측정(미국 미주리주(州) - 세인트루이스주)루이스)

[24] F. G. Meyer와 R. R. Coifman(1997) 응용 및 계산 고조파 분석 4:147.

[25] A. G. Flesia, H. Hel-Or, A.Averbucch, E. J. Candes, R. R. Coifman 및 D. L. Donoho (2001) 리지렛 패킷의 디지털 실장(Academical Press, New York).

[26] Shi, J.; Zhang, N.-T.; Liu, X.-P. (2011). "A novel fractional wavelet transform and its applications". Sci. China Inf. Sci. 55 (6): 1270–1279. doi:10.1007/s11432-011-4320-x.

[27] A.N. Akansu, W.A. Serdijn 및 I.W. Selesnick, 웨이브릿의 새로운 응용 프로그램: 리뷰, 물리 커뮤니케이션, 엘세비어, 제3호, 제1, 페이지 1-18, 2010년 3월.

[galli-28] Stefano Galli; O. Logvinov (July 2008). "Recent Developments in the Standardization of Power Line Communications within the IEEE". IEEE Communications Magazine. 46 (7): 64–71. doi:10.1109/MCOM.2008.4557044. S2CID 2650873. P1901 PHY/MAC 제안 개요

[29] Wotherspoon, T.; et., al. (2009). "Adaptation to the edge of chaos with random-wavelet feedback". J. Phys. Chem. 113 (1): 19–22. Bibcode:2009JPCA..113...19W. doi:10.1021/jp804420g. PMID 19072712.

[30] Abbott, Benjamin P.; et al. (LIGO Scientific Collaboration and Virgo Collaboration) (2016). "Observing gravitational-wave transient GW150914 with minimal assumptions". Phys. Rev. D. 93 (12): 122004. arXiv:1602.03843. Bibcode:2016PhRvD..93l2004A. doi:10.1103/PhysRevD.93.122004. S2CID 119313566.

[31] V Necula, S Klimenko and G Mitselmakher (2012). "Transient analysis with fast Wilson-Daubechies time-frequency transform". Journal of Physics: Conference Series. 363 (1): 012032. Bibcode:2012JPhCS.363a2032N. doi:10.1088/1742-6596/363/1/012032.

[32] J. 라피 외보철물을 위한 전완 EMG 신호의 기능 추출, Expert Systems with Applications 38 (2011) 4058–67.

[33] J. 라피 외신호 처리 기술을 사용한 여성 성반응, Journal of Sexual Medicine 6 (2009) 3086–96. (pdf)

[34] Rafiee, J.; Tse, Peter W. (2009). "Use of autocorrelation in wavelet coefficients for fault diagnosis". Mechanical Systems and Signal Processing. 23 (5): 1554–72. Bibcode:2009MSSP...23.1554R. doi:10.1016/j.ymssp.2009.02.008.

[AgarwalMaheswaranMarwan2018-35] Agarwal, Ankit; Maheswaran, Rathinasamy; Marwan, Norbert; Caesar, Levke; Kurths, Jürgen (November 2018). "Wavelet-based multiscale similarity measure for complex networks" (PDF). The European Physical Journal B. 91 (11): 296. Bibcode:2018EPJB...91..296A. doi:10.1140/epjb/e2018-90460-6. eISSN 1434-6036. ISSN 1434-6028. S2CID 125557123.

[AgarwalMarwanRathinasamy2017-36] Agarwal, Ankit; Marwan, Norbert; Rathinasamy, Maheswaran; Merz, Bruno; Kurths, Jürgen (13 October 2017). "Multi-scale event synchronization analysis for unravelling climate processes: a wavelet-based approach". Nonlinear Processes in Geophysics. 24 (4): 599–611. Bibcode:2017NPGeo..24..599A. doi:10.5194/npg-24-599-2017. eISSN 1607-7946.

[AgarwalCaesarMarwan2019-37] Agarwal, Ankit; Caesar, Levke; Marwan, Norbert; Maheswaran, Rathinasamy; Merz, Bruno; Kurths, Jürgen (19 June 2019). "Network-based identification and characterization of teleconnections on different scales". Scientific Reports. 9 (1): 8808. Bibcode:2019NatSR...9.8808A. doi:10.1038/s41598-019-45423-5. eISSN 2045-2322. PMC 6584743. PMID 31217490.

[38] Matlab Toolbox – URL : http://matlab.izmiran.ru/help/toolbox/wavelet/ch06_a32.html

[39] Erik Hjelmoss (1999-01-21) Gabor Wavelets URL : http://www.ansatt.hig.no/erikh/papers/scia99/node6.html

[40] "How Wavelets Allow Researchers to Transform — and Understand — Data". Quanta Magazine. 2021-10-13. Retrieved 2021-10-20.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[16]

[17]

[18]

[19]

[20]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[38]

[39]

[1]

Search

웨이브릿

네임스페이스

더

목차

어원학

웨이브릿 이론

연속 웨이브릿 변환(연속 시프트 및 스케일 파라미터)

이산 웨이브릿 변환(이산 시프트 및 스케일 파라미터, 시간 내 연속)

다중 해상도 기반 이산 웨이브릿 변환(시간 내 연속)

푸리에 변환과의 비교(연속 시간)

의

필터

★★★

★★★★★★★★★★★★

Transforms( 트랜스폼)

프로그램

의

제거

멀티스케일 기후 네트워크

웨이브릿 목록

이산 웨이브릿

연속 웨이브릿

실수치

복소수치

「」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

Search

웨이브릿

어원학

웨이브릿 이론

연속 웨이브릿 변환(연속 시프트 및 스케일 파라미터)

이산 웨이브릿 변환(이산 시프트 및 스케일 파라미터, 시간 내 연속)

다중 해상도 기반 이산 웨이브릿 변환(시간 내 연속)

푸리에 변환과의 비교(연속 시간)

의

필터

★★★

★★★★★★★★★★★★

Transforms( 트랜스폼)

프로그램

의

제거

멀티스케일 기후 네트워크

웨이브릿 목록

이산 웨이브릿

연속 웨이브릿

실수치

복소수치

「 」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

「」를 참조해 주세요.