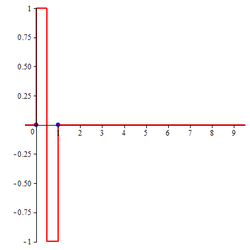
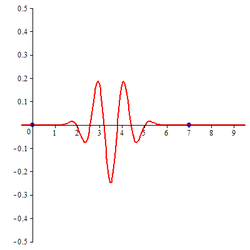
스플라인 함수를 사용하여 파장을 형성함
주문 1, 2, 3, 4, 5의 추기경 B 스플라인 파장을 압축적으로 지원하는 애니메이션. 파도 의 수학적 이론에서, 스플라인 파장은 스플라인 함수 를 사용하여 만들어진 파장이다.[1] 스플라인 파장의 종류는 다양하다. C.K가 도입한 보간성 스플라인 파장. 추이와 J.Z. 왕 교수는 어떤 스플라인 보간식 에 기초하고 있다.[2] 이 웨이블렛은 직교 하지만, 컴팩트 한 지지대를 가지고 있지 않다. B-스플라인 으로 구성되고 콤팩트한 지지대를 갖는 어떤 의미에서는 독특한 종류의 웨이블렛이 있다.비록 이 파도들이 직교하지 않지만, 그들은 그들을 꽤 유명하게 만든 몇몇 특별한 성질을 가지고 있다.[3] spline wavelet 이라는 용어는 이 spline wavelet의 종류에 있는 wavelet을 가리키는 데 가끔 사용된다.이 특별한 파동은 B-분할 파도 와 B-분할 파동이라고 도 불린다.[4] 배틀-르마리 웨이블렛도 스플라인 함수를 이용해 만든 웨이블렛이다.[5]
추기경 B-스플라인스 n 을 음이 아닌 고정 정수 로 한다.Let n n개 의 파생상품 이 어디에서나 연속적 으로 존재하도록 실제 숫자 의 집합에 걸쳐 정의된 모든 실제 가치 함수 집합을 의미한다.bi-infinite −2 sequence . . . . x 1 , x−1 0 , x, x 2 , . 모든 r +1r 에r x < x 그리고 r이 ±10에 가까워질 때 x 가r 매듭 집합이 {x r 순서 n의 스플라인 (spline)은 C 의n S (x )로r , 각 r에 대해 S(x )의 간격 제한(x, x r +1x 의 최대 n 의 실제 도 계수를 갖는 다항식 과 일치한다.
r 이 정수인 x r +1x 는r 추기경 스플라인 이라고 한다.정수 Z = {. . . . . . . . . . . . . . . . . . . . . . . . 정수의 집합은 추기경 스플라인(spline)의 매듭 집합에 대한 표준 선택이다. 달리 명시되지 않는 한 일반적으로 매듭 집합은 정수의 집합이라고 가정한다.
B 스플라인 추기경은 특별한 종류의 추기경 스플라인이다. 임의의 양의 정수 m 에 대해 N m x )으로 표시된 순서 m 의 추기경 B-스플라인(B-spline)은 다음과 같이 재귀적으로 정의된다.
N 1 ( x ) = { 1 0 ≤ x < 1 0 그렇지 않으면 {\displaystyle N_{1}(x)={\begin{case}1&0\leq x<1\\\0&{\text{otherwise}\case}}}} N m x ∫ 1 N 1 x t d t {\displaystyle N_{m}(x)=\int _{0}^{1 }{N_{m-1}(x-t)dt 1 displaystyle m>1 . 모든 순서의 B-분할에 대한 구체적인 표현과 그 그래프는 이 글의 뒷부분에 제시되어 있다.
추기경 B-분할의 속성 기본 속성 N m x {\displaystyle N_{m}(x)} 지원 은 닫힌 간격 0 , m ] {\displaystyle [0,m]} . 함수 N m x {\displaystyle N_{m}(x)} 것 m > 대한 m x {\ displaystyle N_ {m }( x) 0} . ∑ k ∞ N m k {\displaystyle \sum \sum k=-\infit }^{\n_{m}(x-k )= 모든 x . The cardinal B-splines of orders m and m-1 are related by the identity: N m ( x ) = x m − 1 N m − 1 ( x ) + m − x m − 1 N m − 1 ( x − 1 ) {\displaystyle N_{m}(x)={\frac {x}{m-1}}N_{m-1}(x)+{\frac {m-x}{m-1}}N_{m-1}(x-1)} N m (x ){\displaystyle N_{m}(x)} x m 2 {\ displaystyle ={\frac{ 2}}, m ( m N m (m 2 x ){\ displaystysty N_{m}\m}{2}}-x= 대해 대칭이다. N_{m}\왼쪽({\frac {m}{2}}+x\오른쪽)} The derivative of N m ( x ) {\displaystyle N_{m}(x)} N m ′ ( x ) = N m − 1 ( x ) − N m − 1 ( x − 1 ) {\displaystyle N_{m}^{\prime }(x)=N_{m-1}(x)-N_{m-1}(x-1)} ∫ − ∞ ∞ N m ( x ) d x = 1 {\displaystyle \int _{-\ft }^{\n_{m}(x)\,dx=1} 두 척도 관계 순서 m 의 추기경 B-분할은 다음과 같은 두 가지 척도 관계를 만족한다.
N m x ∑ k 0 m 2 m 1 k N m 2 x k {\displaystyle N_{m}(x)=\sum _{k=0}^{m2^{m+1}{m \c선택 }{}{m_{m-k 리에츠 속성 순서 m 의 추기경 B-스플라인(B-spline)은 Riesz 속성으로 알려진 다음과 같은 속성을 만족한다. 정사각형 합계 양면 시퀀스 c k } {\ displaystyle \{c_{k}\}_{k=-\fty }}}}} A {\displaystystyle A} B {\displaystysty B}
A ‖ { c k } ‖ 2 ≤ ‖ ∑ k = − ∞ ∞ c k N m ( x − k ) ‖ 2 ≤ B ‖ { c k } ‖ 2 {\displaystyle A\left\Vert \{c_{k}\}\right\Vert ^{2}\leq \left\Vert \sum _{k=-\infty }^{\infty }c_{k}N_{m}(x-k)\right\Vert ^{2}\leq B\left\Vert \{c_{k}\}\right\Vert ^{2}} 여기서‖ ⋅ {\displaystyle \Vert \cdot \Vert } 2 표준이다.
소목 B형 추기경 추기경 B-분할은 순서 1의 B-분할(즉 1 x {\displaystyle N_{1}(x 컴퓨터 대수 시스템을 사용하여 더 높은 순위의 추기경 B-분열을 위한 구체적인 표현을 얻어야 할 수 있다. 최대 6개 주문의 B-분할 추기경의 구체적인 표현은 다음과 같다. 추기경 B분할의 최대 4개의 순서 그래프도 전시된다. 영상에서, 해당 2-척도의 관계에 기여하는 용어의 그래프도 보여진다. 각 영상의 두 점은 B-스플라인을 지지하는 구간의 극치를 나타낸다.
상수 B-스플라인 순서 1의 B-스플라인, 즉 N 1 x {\displaystyle N_{1}(x)} 에 의해 정의된다.
N 1 ( x ) = { 1 0 ≤ x < 1 0 그렇지 않으면 {\displaystyle N_{1}(x)={\begin{case}1&0\leq x<1\\\0&{\text{otherwise}\case}}}} 이 B-스플라인에 대한 두 가지 척도 관계는
N 1 ( x ) = N 1 ( 2 x ) + N 1 ( 2 x − 1 ) {\displaystyle N_{1}(x)= N_{1}(2x)+N_{1}(2x-1)} 상수 B-스플라인 N 1 ( x ) {\displaystyle N_{1}(x)}
선형 B-스플라인 순서 2의 B-스플라인, 즉 N x {\displaystyle N_{2}(x)} . 그것은 에 의해 주어진다.
N 2 ( x ) = { x 0 ≤ x < 1 − x + 2 1 ≤ x < 2 0 그렇지 않으면 {\displaystyle N_{2}(x)={\begin}x&0\leq x<1\\-x+2&1\leq x<2\\\0&{\text{otherwise}\case}}}}}} 이 파랑의 두 축척 관계는
N 2 ( x ) = 1 2 N 2 ( 2 x ) + N 2 ( 2 x − 1 ) + 1 2 N 2 ( 2 x − 2 ) {\displaystyle N_{2}(x)={\frac {1}{1}{2}}N_{2}(2x)+N_{2}(2x-1)+{\frac {1}{1}{2}}N_{2}(2x-2)}} 선형 B-스플라인 N 2 ( x ) {\displaystyle N_{2}(x)}
2차 B-스플라인 순서 3의 B-스플라인, 즉 N 3 x {\displaystyle N_{3}(x)} 그것은 에 의해 주어진다.
N 3 ( x ) = { 1 2 x 2 0 ≤ x < 1 − x 2 + 3 x − 3 2 1 ≤ x < 2 1 2 x 2 − 3 x + 9 2 2 ≤ x < 3 0 그렇지 않으면 {\displaystyle N_{3}(x)={\begin{cases}{\frac {1}{2}}x^{2}&0\leq x<1\\-x^{2}+3x-{\frac {3}{2}}&1\leq x<2\\{\frac {1}{2}}x^{2}-3x+{\frac {9}{2}}&2\leq x<3\\0&{\text{otherwise}}\end{cases}}} 이 파랑의 두 축척 관계는
N 3 ( x ) = 1 4 N 3 ( 2 x ) + 3 4 N 3 ( 2 x − 1 ) + 3 4 N 3 ( 2 x − 2 ) + 1 4 N 3 ( 2 x − 3 ) {\displaystyle N_{3}(x)={\frac {1}{4}}N_{3}(2x)+{\frac {3}{4}}N_{3}(2x-1)+{\frac {3}{4}}N_{3}(2x-2)+{\frac {1}{4}}N_{3}(2x-3)} 2차 B-스플라인 N 3 ( x ) {\displaystyle N_{3}(x)}
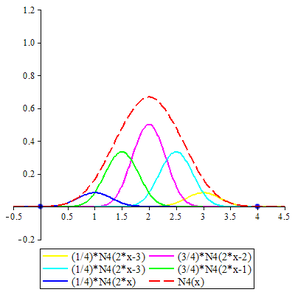
큐빅 B-스플라인 입방 B-스플라인(cubmit B-스플라인 , displaystyle N_{4}( .
N 4 ( x ) = { 1 6 x 3 0 ≤ x < 1 − 1 2 x 3 + 2 x 2 − 2 x + 2 3 1 ≤ x < 2 1 2 x 3 − 4 x 2 + 10 x − 22 3 2 ≤ x < 3 − 1 6 x 3 + 2 x 2 − 8 x + 32 3 3 ≤ x < 4 0 그렇지 않으면 {\displaystyle N_{4}(x)={\begin{cases}{\frac {1}{6}}x^{3}&0\leq x<1\\-{\frac {1}{2}}x^{3}+2x^{2}-2x+{\frac {2}{3}}&1\leq x<2\\{\frac {1}{2}}x^{3}-4x^{2}+10x-{\frac {22}{3}}&2\leq x<3\\-{\frac {1}{6}}x^{3}+2x^{2}-8x+{\frac {32}{3}}&3\leq x<4\\0&{\text{otherwise}}\end{cases}}} 입방 B-스플라인에 대한 두 가지 척도 관계는
N 4 ( x ) = 1 8 N 4 ( 2 x ) + 1 2 N 4 ( 2 x − 1 ) + 3 4 N 4 ( 2 x − 2 ) + 1 2 N 4 ( 2 x − 3 ) + 1 8 N 4 ( 2 x − 4 ) {\displaystyle N_{4}(x)={\frac {1}{8}}N_{4}(2x)+{\frac {1}{2}}N_{4}(2x-1)+{\frac {3}{4}}N_{4}(2x-2)+{\frac {1}{2}}N_{4}(2x-3)+{\frac {1}{8}}N_{4}(2x-4)} 큐빅 B-스플라인 N 4 ( x ) {\displaystyle N_{4}(x)}
비고 : 노란색 그래프 4 N 4 2 x 4 {\displaystyle {\frac }{4}N_{4}( .
양분 B-스플라인 이차수 B-스플라인(bi-quadratic N 5 {\displaystyle N_{5}(x)} .
N 5 ( x ) = { 1 24 x 4 0 ≤ x < 1 − 1 6 x 4 + 5 6 x 3 − 5 4 x 2 + 5 6 x − 5 24 1 ≤ x < 2 1 4 x 4 − 5 2 x 3 + 35 4 x 2 − 25 2 x + 155 24 2 ≤ x < 3 − 1 6 x 4 + 5 2 x 3 − 55 4 x 2 + 65 2 x − 655 24 3 ≤ x < 4 1 24 x 4 − 5 6 x 3 + 25 4 x 2 − 125 6 x + 625 24 4 ≤ x < 5 0 그렇지 않으면 {\displaystyle N_{5}(x)={\begin{cases}{\frac {1}{24}}x^{4}&0\leq x<1\\-{\frac {1}{6}}x^{4}+{\frac {5}{6}}x^{3}-{\frac {5}{4}}x^{2}+{\frac {5}{6}}x-{\frac {5}{24}}&1\leq x<2\\{\frac {1}{4}}x^{4}-{\frac {5}{2}}x^{3}+{\frac {35}{4}}x^{2}-{\frac {25}{2}}x+{\frac {155}{24}}&2\leq x<3\\-{\frac {1}{6}}x^{4}+{\frac {5}{2}}x^{3}-{\frac {55}{4}}x^{2}+{\frac {65}{2}}x-{\frac {655}{24}}&3\leq x<4\\{\frac {1}{24}}x^{4}-{\frac {5}{6}}x^{3}+{\frac {25}{4}}x^{2}-{\frac {125}{6}}x+{\frac {625}{24}}&4\leq x<5\\0&{\text{otherwise}}\end{cases}}} 두 척의 관계는
N 5 ( x ) = 1 16 N 5 ( 2 x ) + 5 16 N 5 ( 2 x − 1 ) + 10 16 N 5 ( 2 x − 2 ) + 10 16 N 5 ( 2 x − 3 ) + 5 16 N 5 ( 2 x − 4 ) + 1 16 N 5 ( 2 x − 5 ) {\displaystyle N_{5}(x)={\frac {1}{16}}N_{5}(2x)+{\frac {5}{16}}N_{5}(2x-1)+{\frac {10}{16}}N_{5}(2x-2)+{\frac {10}{16}}N_{5}(2x-3)+{\frac {5}{16}}N_{5}(2x-4)+{\frac {1}{16}}N_{5}(2x-5)} 퀸틱 B-스플라인 5중 B-스플라인(B-spline)은 N 6 (x ) {\displaystyle N_{6}(x)} .
N 6 ( x ) = { 1 120 x 5 0 ≤ x < 1 − 1 24 x 5 + 1 4 x 4 − 1 2 x 3 + 1 2 x 2 − 1 4 x + 1 20 1 ≤ x < 2 1 12 x 5 − x 4 + 9 2 x 3 − 19 2 x 2 + 39 4 x − 79 20 2 ≤ x < 3 − 1 12 x 5 + 3 2 x 4 − 21 2 x 3 + 71 2 x 2 − 231 4 x + 731 20 3 ≤ x < 4 1 24 x 5 − x 4 + 19 2 x 3 − 89 2 x 2 + 409 4 x − 1829 20 4 ≤ x < 5 − 1 120 x 5 + 1 4 x 4 − 3 x 3 + 18 x 2 − 54 x + 324 5 5 ≤ x < 6 0 그렇지 않으면 {\displaystyle N_{6}(x)={\begin{cases}{\frac {1}{120}}x^{5}&0\leq x<1\\-{\frac {1}{24}}x^{5}+{\frac {1}{4}}x^{4}-{\frac {1}{2}}x^{3}+{\frac {1}{2}}x^{2}-{\frac {1}{4}}x+{\frac {1}{20}}&1\leq x<2\\{\frac {1}{12}}x^{5}-x^{4}+{\frac {9}{2}}x^{3}-{\frac {19}{2}}x^{2}+{\frac {39}{4}}x-{\frac {79}{20}}&2\leq x<3\\-{\frac {1}{12}}x^{5}+{\frac {3}{2}}x^{4} -{\frac {21}{2}}x^{3}+{\frac {71}{2}}x^{2}-{\frac {231}{4}}x+{\frac {731}{20}}&3\leq x<4\\{\frac {1}{24}}x^{5}-x^{4}+{\frac {19}{2}}x^{3}-{\frac {89}{2}}x^{2}+{\frac {409}{4}}x-{\frac {1829}{20}}&4\leq x<5\\-{\frac {1}{120}}x^{5}+{\frac {1}{4}}x^{4}-3x^{3}+18x^{2}-54x+{\frac {324}{5}}&5\leq x<6\\0&{\text{otherwise}}\end{cases}}} 추기경 B-분할에 의해 생성된 다중 분해능 분석 순서 m 의N m x {\displaystyle N_{m}(x)} 다중 분해능 분석 을 생성한다. 실제로 위에서 설명한 이러한 기능의 기본 속성으로부터, 기능 N m {\displaystyle N_{m}(x)} 사각형 통합 이 가능하고2 R {\displaystyle L^{2}(R) 다중 분해능 분석을 설정하려면 다음과 같은 공식을 사용한다.
모든 정수 k j {\displaystyle k, j } N k j N m k x j {\displaystyle N_{m,kj}(x)= N_{m}(2^{k}x-j)} For each integer k {\displaystyle k} V k {\displaystyle V_{k}} L 2 ( R ) {\displaystyle L^{2}(R)} closure of the linear span of the set { N m , k j ( x ) : j = ⋯ , − 2 , − 1 , 0 , 1 , 2 , ⋯ } {\displaystyle \{N_{m,kj}(x):j=\cdots ,-2,-1,0,1,2,\cdots \}} 이러한 분석들이 다해상도 분석을 정의한다는 것은 다음과 같다.
The spaces V k {\displaystyle V_{k}} ⋯ ⊂ V − 2 ⊂ V − 1 ⊂ V 0 ⊂ V 1 ⊂ V 2 ⊂ ⋯ {\displaystyle \cdots \subset V_{-2}\subset V_{-1}\subset V_{0}\subset V_{1}\subset V_{2}\subset \cdots } 모든 V {\ displaystyle V_{k} L 2 R {\displaystyle ^{2}(R)} L 2 R {\displaystyle ^{2}(R)} . 모든 서브 스페이스 V k {\ displaystyle V_{k}} 우주 X에 각 정수 들어)Vk{\displaystyle V_{km그리고 4.9초 만}에}}은 아무런 조건이 없는 기준}. 집합을{Nm, kj()):j)⋯, − 2, − 1,0,1,2, ⋯}{\displaystyle\와 같이{N_{m,kj}()):j=\cdots ,-2,-1,0,1,2,\cdots{k\displaystyle}k(은 바나흐 공간 X에서 일련{xn}은 아무런 조건이 없는 기초 모든 permutatio.n 시퀀스 {x n 공간 X)[6] 추기경 B-스플라인에서 나온 웨이블렛 m 을 고정된 양의 정수로 하고 N x {\displaystyle N_{m}(x)} 순서 m의 기본 B-스플라인으로A function ψ m ( x ) {\displaystyle \psi _{m}(x)} L 2 ( R ) {\displaystyle L^{2}(R)} N m ( x ) {\displaystyle N_{m}(x)} L 2 ( R ) {\displaystyle L^{2}(R)} { ψ m ( x − j ) : j = ⋯ , − 2 , − 1 , 0 , 1 , 2 , ⋯ } {\displaystyle \{\psi _{m}(x-j):j=\cdots ,-2,-1,0,1,2,\cdots \}} W 0 {\displaystyle W_{0}} orthogonal complement of V 0 {\displaystyle V_{0}} V 1 {\displaystyle V_{1}} ψm x {\displaystyle \psi _{m}(x)} m 은 ψm x {\displaystyle \psi _{m}(x)} m 의 B-spline과 관련된 기본 파장임을추기경 B-spline N m x mm ( ) \displaystyle \ psi _{m}(x) , 다음
기본 보간 스플라인을 이용한 B-스플라인 상대 웨이블릿 기본 보간 스플라인 정의들 m 을 고정 양의 정수 m x {\displaystyle m}(x ( m 의 B-spline으로 한다Given a sequence { f j : j = ⋯ , − 2 , − 1 , 0 , 1 , 2 , ⋯ } {\displaystyle \{f_{j}:j=\cdots ,-2,-1,0,1,2,\cdots \}} { c m , k : k = ⋯ , − 2 , − 1 , 0 , 1 , 2 , ⋯ } {\displaystyle \{c_{m,k}:k=\cdots ,-2,-1,0,1,2,\cdots \}}
∑ k c m N m j m 2 k f j {\ displaystyle \sum _{k=-\inforty }^{{m,}N_{m}\reft(j+{{m}{2}}-k\ 오른쪽 )=f_{j }, j. 기본 스플라인 보간 문제 로 알려져 있다.시퀀스 f j }{\displaystyle \{f_{j}\}}}} 0 j {\ displaystyle \delta _ {0j 여기 Δ i displaysty \delta _ ij } Δ j
Δ i j , i j 0 , i {\ displaystyle \property_{ij}={\case} case}{} j\0, text{}}}}, } i\neq \end{ }}}}}, 기본적인 스플라인 보간 문제야 문제의 해결은 순서 m 의 기본적인 보간성 스플라인 을 산출한다. 이 스플라인에는 L m x {\displaystyle L_{m}(x)}
L m ( x ) = ∑ k = − ∞ ∞ c m , k N m ( x + m 2 − k ) {\displaystyle L_{m}(x)=\sum _{k=--\inflit }^{{m,k}N_{m}\왼쪽(x+{m}{2}}-k\오른쪽)}} 여기서 시퀀스 c m, k } {\displaystyle \{c_{m,k}\}\}}
∑ k = − ∞ ∞ c m k N m ( j + m 2 − k ) = δ 0 j {\displaystyle \sum _{k=-\inflt }^{}c_{m,k}N_{m}\왼쪽(j+{\frac{m}{2}}-k\right)=\delta _{0j} 인 기본적인 보간성 스플라인 L m {\displaystyle L_{m}(x)} 변환 을 사용하여 결정할 수 있다 다음 표기 사용
A ( z ) = ∑ k = − ∞ ∞ δ k 0 z k = 1 nothystyle A(z)=\{k=\ft ^{k0}z^1,}}} B m ( z ) = ∑ k = − ∞ ∞ N m ( k + m 2 ) z k {\displaystyle B_{m}(z)=\sum _{k=--\inflit }^{{n_}\{m}\좌측(k+{\frac{m}{2}}\오른쪽)z^{k}}}}}} C m ( z ) = ∑ k = − ∞ ∞ c m k z k k=-\ }{displaysty C_{m=\infit ^{{}}}}}}}}}}}}}}}}}} 는c, k {\ displaystyle c_{m,k}
B m ( z ) C m ( z ) = A ( z ) displaystyle B_{m}(z)_{m}(z)=A(z)} 우리가 얻는 것
C m z 1 B {\ displaystyle C_{m}(z)={\frac {1}{B_{m}(z 이것 m k {\ displaystyle c_{m,k}} .
구체적인 예로 사례 L 4 x {\displaystyle L_{4}(x)} B m z {\displaystyle B_{m}(z)}
B 4 ( x ) = ∑ k = − ∞ ∞ N 4 ( 2 + k ) z k {\displaystyle B_{4}(x)=\sum _{k=--\ft }^{\n_{4}(2+k)z^{k}}}}}} N 4 (k 2 {\displaystyle N_{4}(k+2 k 1 , 1 {\displaystyle k=-1,0,
N 4 ( 1 ) = 1 6 , N 4 ( 2 ) = 4 6 , N 4 ( 3 ) = 1 6 . {\displaystyle N_{4}(1)={\frac {1}{1}{6},N_{4}(2)={\frac {4}{6},N_{4}(3)={\frac {1}{6}}. } 따라서 B 4 z {\displaystyle B_{4}(z)}
B 4 ( z ) = 1 6 z − 1 + 4 6 z 0 + 1 6 z 1 = 1 + 4 z + z 2 6 z {\displaystyle B_{4}(z)={\frac {1}{6}z^{-1}+{4}{6}{6}}}z^{0}+{6}z^{1}{1}}}={\frac {1+4z+z^{6z}}}}}}}}}}}{6z}}}}}}}}}}}}}}}}}}}}}}}. 이것 4 {\displaystyle C_{4}(z)} .
C 4 ( z ) = 6 z 1 + 4 z + z 2 {\displaystyle C_{4}(z)={\frac {6z}{1+4z+z^{2}}: 이 식을 부분 분수로 나누고 각 항을 환상 영역에서 z 의 힘으로 확장하면 c 4 k {\ displaystyle c_{4,k} 그런 다음 이러한 값은 L 4 x {\displaystyle L_{4}(x)
L 4 ( x ) = ∑ k = − ∞ ∞ ( − 1 ) k 3 ( 2 − 3 ) k N 4 ( x + 2 − k ) {\displaystyle L_{4}(x)=\sum _{k=-\infit }^{k}{3}{\sqrt{3}}^{}{{{{\sqrt{3}}}}{{{{{{}}}}}}{{{{{{N_}(x+2-k)})}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} 기본 보간 스플라인을 이용한 웨이브레트 양의 정수 m 의 경우 bym (x {\displaystyle \psi _{m}(x)}
ψ I , m ( x ) = d m d x m L 2 m ( 2 x − 1 ) {\displaystyle \psi _{I,m}(x)={\frac {d^{m}{dx^{m}}L_{2m}(2x-1)} 순서 N m x {\displaystyle N_{m}(x)} . ψ I m {\ displaystyle \psi _{I,m} 첨자 는 보간성 스플라인 공식에 기초하고 있음을 나타내는 데 사용된다이 기본 웨이브는 압축적으로 지지되지 않는다.
예 보간 스플라인을 사용한 순서 2의 웨이블렛은 다음 명령을 통해 제공된다.
ψ I , 2 ( x ) = d 2 d x 2 L 4 ( 2 x − 1 ) {\displaystyle \psi _{I,2}(x)={\frac {d^{2}}{dx^{2}}L_{4}(2x-1)} 이제 4 x {\displaystyle L_{4}(x)}
ψ I , 2 ( x ) = d 2 d x 2 ∑ k = − ∞ ∞ ( − 1 ) k 3 ( 2 − 3 ) k N 4 ( 2 x + 1 − k ) {\displaystyle \psi _{I,2}(x)={\frac {d^{2}}{dx^{2}}}\sum _{k=-\infty }^{\infty }(-1)^{k}{\sqrt {3}}(2-{\sqrt {3}})^{ k }N_{4}(2x+1-k)} 이제 N m 1 x {\displaystyle N_{m}(x)} {\displaystyle N_{m-1(x)} ψ 2 x {\displaysty \psi _{2(x)}
ψ I , 2 ( x ) = ∑ k = − ∞ ∞ ( − 1 ) k 4 3 ( 2 − 3 ) k ( ( N 2 ( 2 x + k − 1 ) − 2 N 2 ( 2 x + k − 2 ) + N 2 ( 2 x + k − 3 ) ) {\displaystyle \psi _{I,2}(x)=\sum _{k=-\infty }^{\infty }(-1)^{k}4{\sqrt {3}}(2-{\sqrt {3}})^{ k }{\Big (}(N_{2}(2x+k-1)-2N_{2}(2x+k-2)+ N_{2}(2x+k-3){ \Big )}}} 다음 조각의 선형 함수는 ψ 2 x {\displaystyle \ psi _{2}(x)} 식 3 displaystyle k=-3,\ldots ψ x {\displaystyle \psi \{2}(x) .
ψ I , 2 ( x ) ≈ { 0.07142668 x + 0.17856670 − 2.5 < x ≤ − 2 − 0.48084803 x − 0.92598272 − 2 < x ≤ − 1.5 2.0088293 x + 2.8085333 − 1.5 < x ≤ − 1 − 7.5684795 x − 6.7687755 − 1 < x ≤ − 0.5 28.245949 x + 11.138439 − 0.5 < x ≤ 0 − 57.415316 x + 11.138439 0 < x ≤ 0.5 57.415316 x − 46.276878 0.5 < x ≤ 1 − 28.245949 x + 39.384388 1 < x ≤ 1.5 7.5684795 x − 14.337255 1.5 < x ≤ 2 − 2.0088293 x + 4.8173625 2 < x ≤ 2.5 0.48084803 x − 1.4068308 2.5 < x ≤ 3 − 0.07142668 x + 0.24999338 3 < x ≤ 3.5 0 o t h e r w i s e {\displaystyle \psi _{I,2}(x)\trawth {\begin}0.07142668x+0.17856670&-2. 5<x\leq -2\\-0.48084803x-0.92598272&-2<x\leq -1.5\\2.0088293x+2.8085333&-1.5<x\leq -1\\-7.5684795x-6.7687755&-1<x\leq -0.5\\28.245949x+11.138439&-0.5<x\leq 0\\-57.415316x+11.138439&0<x\leq 0.5\\57.415316x-46.276878&0.5<x\leq 1\\-28.245949x+39.384388&1<x\leq 1.5\\7.5684795x-14.337255&1. 5<x\leq 2\\-2.0088293x+4.8173625&2<x\leq 2.5\\\0.1684803x-1.4068308&2. 5<x\leq 3\\-0.07142668x+0.2499338&3<x\leq 3.5\\\0&{pair}\end{case}}}}} 두 척도 관계 wavelet 함수 ψ x {\displaystyle \psi _{m}(x)}
ψ I , m ( x ) = ∑ − ∞ ∞ q n N m ( 2 x − n ) {\displaystyle \psi _{I,m}(x)=\sum _{-\infty }^{\infty }q_{n}N_{m}(2x-n)} q n = ∑ j = 0 m ( − 1 ) j ( m j ) c m + n − j − 1 . {\displaystyle q_{n}=\sum _{j=0}^{m}(-1)^{j}{m \choose j}c_{m+n-j-1}. } 콤팩트하게 지원되는 B-스플라인 웨이브 보간파장을 사용하여 생성된 스플라인 파장은 압축적으로 지지되지 않는다. 압축적으로 지지되는 B-분할 파동은 찰스 K에 의해 발견되었다. 추이와 지안중 왕씨로 1991년에 출판되었다.[3] [7] The compactly supported B-spline wavelet relative to the cardinal B-spline N m ( x ) {\displaystyle N_{m}(x)} m discovered by Chui and Wong and denoted by ψ C , m ( x ) {\displaystyle \psi _{C,m}(x)} [ 0 , 2 m − 1 ] {\displaystyle [0,2m-1]} 이 파도들은 아래에서 설명하는 어떤 의미에서는 본질적으로 독특하다.
정의 오더 m 의 B-스플라인 파장은 다음과 같이 압축적으로 지원된다.
ψ C , m ( x ) = 1 2 2 m − 1 ∑ j = 0 2 m − 2 ( − 1 ) j N 2 m ( j + 1 ) d m d x m N 2 m ( 2 x − j ) {\displaystyle \psi _{C,m}(x)={\frac {1}{2^{2m-1}}}\sum _{j=0}^{2m-2}(-1)^{j}N_{2m}(j+1){\frac {d^{m}}{dx^{m}}}N_{2m}(2x-j)} 이것은 m번째 주문 스플라인이다. 특별한 경우로서, 오더 1의 B-스플라인 파슬릿이 콤팩트하게 지지되고 있다.
ψ C , 1 ( x ) = 1 2 N 2 ( 1 ) d d x N 2 ( 2 x ) = { 1 0 ≤ x < 1 2 − 1 1 2 ≤ x < 1 0 그렇지 않으면 {\displaystyle \psi _{C,1}(x)={\frac {1}{1}{2}}N_{2}(1){\frac {d}{dx}}}}}} N_{2}(2x)={\begin{case}1&0\leq x<{\frac {1}{1}{1}\-1&{\frac {1}{1}:{1}:{1}:{1}:{1}:{1}{1}}\leq x<1\0&{\text}{otherwise}}}}}}}}}}}}}} 잘 알려진 하르 파도타기 입니다.
특성. ψ C m x {\displaystyle \psi _{C,m}(x)} 0 , 2m 1 ] {\displaystyle [0,2m-1]} . wavelet ψ C m x {\displaystyle \psi _{C,m}(x)} If η ( x ) ∈ W 0 {\displaystyle \eta (x)\in W_{0}} W 0 {\displaystyle W_{0}} 2 m − 1 {\displaystyle 2m-1} η ( x ) = c 0 ψ C , m ( x − n 0 ) {\displaystyle \eta (x)=c_{0}\psi _{C,m}(x-n_{0})} c 0 {\displayst yle c_{0}} 일부 displaystyle {0} . [8] ψ C m x {\displaystyle \psi _{C,m}(x)} m 에 대칭이고m 에 대칭이다.두 척도 관계 ψm x {\displaystyle \property _{m}(x)}
ψ C , m ( x ) = ∑ n = 0 3 m − 2 q n N m ( 2 x − n ) {\displaystyle \psi _{C,m}(x)=\sum _{n=0}^{3m-2}q_{n}N_{m}(2x-n)} q n = ( − 1 ) n 2 m − 1 ∑ j = 0 m ( m j ) N 2 m ( n − j + 1 ) {\displaystyle q_{n}={\frac {(-1)^{n}}{2^{m-1}}}\sum _{j=0}^{m}{m \choose j}N_{2m}(n-j+1)} 분해관계 압축적으로 지원되는 B-스플라인 파슬릿의 분해 관계는 다음과 같은 형태를 가진다.
N m ( 2 x − l ) = ∑ k = − ∞ ∞ [ a m , l − 2 k N m ( x − k ) + b m , l − 2 k ψ C , m ( x − k ) ] {\displaystyle N_{m}(2x-l)=\sum _{k=-\infit }^{\infit }\왼쪽[a_,l-2k}N_{m}(x-k)+b_{m,l-2k}\psi _{C,m}(x-k)\rig} 여기서a m, j {\ displaystyle a_{m,j} m, j {\ displaystyle b_{m,j}
a m , j = − ( − 1 ) j 2 ∑ l = − ∞ ∞ q − j + 2 m − 2 l + 1 c 2 m , l , {\displaystyle a_{m,j}=-{\frac {(1)^{j}}{2}}\sum _{l=-\infl}^{{l=-\infl_{-j+2m-2l+1}c_{2m,l}} b m , j = ( − 1 ) j 2 ∑ l = − ∞ ∞ p − j + 2 m − 2 l + 1 c 2 m , l . {\displaystyle b_{m,j}={\frac {(1)-^{j}}{2}}\sum _{l=-\nfl}^{{l=-\fl}{p_{-j+2m-2l+1}c_{2m,l} } 여기서 순서 c 2m , l {\ displaystyle c_{2m,l} m 의 기본 보간형 추기경 스플라인 파장의 계수 순서다
소규모 주문의 B-분할 파장을 압축적으로 지원 오더 1의 B-스플라인 파장을 콤팩트하게 지지 순서가 1인 B-분할 파장에 대한 2-척도의 관계는 다음과 같다.
ψ C , 1 ( x ) = N 1 ( 2 x ) − N 1 ( 2 x − 1 ) {\displaystyle \psi _{C,1}(x)= N_{1}(2x)-N_{1}(2x-1)} 순서 1의 콤팩트하게 지원되는 B-스플라인 파장에 대한 닫힌 폼 표현은
ψ C , 1 ( x ) = { 1 0 ≤ x < 1 2 − 1 1 2 ≤ x < 1 0 그렇지 않으면 {\displaystyle \psi _{C,1}(x)={\begin{pase}1&0\leq x<{1}{\frac{1}{1}{1}{1}{1}{1}}\frac {1}{1}{{1}}}}\req x 1\0&{otherwise}\case}}}}}}}}}}}}}}}}}}}}}\case}}}}}}} 주문 2의 B-스플라인 파슬릿을 콤팩트하게 지지 2차 순서의 B-분할 파장에 대한 2-척도 관계는
ψ C , 2 ( x ) = 1 12 ( N 2 ( 2 x ) − 6 N 2 ( 2 x − 1 ) + 10 N 2 ( 2 x − 2 ) − 6 N 2 ( 2 x − 3 ) + N 2 ( 2 x − 4 ) ) {\displaystyle \psi \c,2}(x)={\frac {1}{1}{12}\좌측(N_{2}-6N_{2}(2x-1)+10N_{2}(2x-2)-6N_{2}(2x-3)+{2}-{2}-{2}(2x-3)+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ N_{2}(2x-4)\오른쪽)} 순서 2의 콤팩트하게 지원되는 B-스플라인 파장을 위한 폐쇄형 표현은
ψ C , 2 ( x ) = { 1 6 x 0 ≤ x < 1 2 − 7 6 x + 2 3 1 2 ≤ x < 1 8 3 x − 19 6 1 ≤ x < 3 2 − 8 3 x + 29 6 3 2 ≤ x < 2 7 6 x − 17 6 2 ≤ x < 5 2 − 1 6 x + 1 2 5 2 ≤ x < 3 0 otherwise {\displaystyle \psi _{C,2}(x)={\begin{cases}{\frac {1}{6}}x&0\leq x<{\frac {1}{2}}\\-{\frac {7}{6}}x+{\frac {2}{3}}&{\frac {1}{2}}\leq x<1\\{\frac {8}{3}}x-{\frac {19}{6}}&1\leq x<{\frac {3}{2}}\\-{\frac {8}{3}}x+{\frac {29}{6}}&{\frac {3}{2}}\leq x<2\\{\frac {7}{6}}x-{\frac {17}{6}}&2\leq x<{\frac {5}{2}}\\-{\frac {1}{6}}x+{\frac {1}{2}}&{\frac {5}{2}}\leq x<3\\0&{\text{otherwise}}\end{cases}}} Compactly supported B-spline wavelet of order 3 The two-scale relation for the compactly supported B-spline wavelet of order 3 is
ψ C , 3 ( x ) = 1 480 [ ( N 3 ( 2 x ) − 29 N 3 ( 2 x − 1 ) + 147 N 3 ( 2 x − 2 ) − 303 N 3 ( 2 x − 3 ) + {\displaystyle \psi _{C,3}(x)={\frac {1}{480}}{\Big [}(N_{3}(2x)-29N_{3}(2x-1)+147N_{3}(2x-2)-303N_{3}(2x-3)+} 303 N 3 ( 2 x − 4 ) − 147 N 3 ( 2 x − 5 ) + 29 N 3 ( 2 x − 6 ) − N 3 ( 2 x − 7 ) ] {\displaystyle 303N_{3}(2x-4)-147N_{3}(2x-5)+29N_{3}(2x-6)-N_{3}(2x-7){\Big ]}} The closed form expression for compactly supported B-spline wavelet of order 3 is
ψ C , 3 ( x ) = { 1 240 x 2 0 ≤ x < 1 2 − 31 240 x 2 + 2 15 x − 1 30 1 2 ≤ x < 1 103 120 x 2 − 221 120 x + 229 240 1 ≤ x < 3 2 − 313 120 x 2 + 1027 120 x − 1643 240 3 2 ≤ x < 2 22 5 x 2 − 779 40 x + 339 16 2 ≤ x < 5 2 − 22 5 x 2 + 981 40 x − 541 16 5 2 ≤ x < 3 313 120 x 2 − 701 40 x + 2341 80 3 ≤ x < 7 2 − 103 120 x 2 + 809 120 x − 3169 240 7 2 ≤ x < 4 31 240 x 2 − 139 120 x + 623 240 4 ≤ x < 9 2 − 1 240 x 2 + 1 24 x − 5 48 9 2 ≤ x < 5 0 otherwise {\displaystyle \psi _{C,3}(x)={\begin{cases}{\frac {1}{240}}x^{2}&0\leq x<{\frac {1}{2}}\\-{\frac {31}{240}}x^{2}+{\frac {2}{15}}x-{\frac {1}{30}}&{\frac {1}{2}}\leq x<1\\{\frac {103}{120}}x^{2}-{\frac {221}{120}}x+{\frac {229}{240}}&1\leq x<{\frac {3}{2}}\\-{\frac {313}{120}}x^{2}+{\frac {1027}{120}}x-{\frac {1643}{240}}&{\frac {3}{2}}\leq x<2\\{\frac {22}{5}}x^{2}-{\frac {779}{40}}x+{\frac {339}{16}}&2\leq x<{\frac {5}{2}}\\-{\frac {22}{5}}x^{2}+{\frac {981}{40}}x-{\frac {541}{16}}&{\frac {5}{2}}\leq x<3\\{\frac {313}{120}}x^{2}-{\frac {701}{40}}x+{\frac {2341}{80}}&3\leq x<{\frac {7}{2}}\\-{\frac {103}{120}}x^{2}+{\frac {809}{120}}x-{\frac {3169}{240}}&{\frac {7}{2}}\leq x<4\\{\frac {31}{240}}x^{2}-{\frac {139}{120}}x+{\frac {623}{240}}&4\leq x<{\frac {9}{2}}\\-{\frac {1}{240}}x^{2}+{\frac {1}{24}}x-{\frac {5}{48}}&{\frac {9}{2}}\leq x<5\\0&{\text{otherwise}}\end{cases}}} Compactly supported B-spline wavelet of order 4 The two-scale relation for the compactly supported B-spline wavelet of order 4 is
ψ C , 4 ( x ) = 1 40320 [ N 4 ( 2 x ) − 124 N 4 ( 2 x − 1 ) + 1677 N 4 ( 2 x − 2 ) − 7904 N 4 ( 2 x − 3 ) + 18482 N 4 ( 2 x − 4 ) − {\displaystyle \psi _{C,4}(x)={\frac {1}{40320}}{\Big [}N_{4}(2x)-124N_{4}(2x-1)+1677N_{4}(2x-2)-7904N_{4}(2x-3)+18482N_{4}(2x-4)-} 24264 N 4 ( 2 x − 5 ) + 18482 N 4 ( 2 x − 6 ) − 7904 N 4 ( 2 x − 7 ) + 1677 N 4 ( 2 x − 8 ) − 124 N 4 ( 2 x − 9 ) + N 4 ( 2 x − 10 ) ] {\displaystyle 24264N_{4}(2x-5)+18482N_{4}(2x-6)-7904N_{4}(2x-7)+1677N_{4}(2x-8)-124N_{4}(2x-9)+N_{4}(2x-10){\Big ]}} The closed form expression for compactly supported B-spline wavelet of order 4 is
ψ C , 4 ( x ) = { 1 30240 x 3 0 ≤ x < 1 2 − 127 30240 x 3 + 2 315 x 2 − 1 315 x + 1 1890 1 2 ≤ x < 1 19 280 x 3 − 47 224 x 2 + 2147 10080 x − 103 1440 1 ≤ x < 3 2 − 1109 2520 x 3 + 465 224 x 2 − 32413 10080 x + 16559 10080 3 2 ≤ x < 2 5261 3360 x 3 − 33463 3360 x 2 + 42043 2016 x − 145193 10080 2 ≤ x < 5 2 − 35033 10080 x 3 + 93577 3360 x 2 − 148517 2016 x + 216269 3360 5 2 ≤ x < 3 4832 945 x 3 − 27691 560 x 2 + 113923 720 x − 28145 168 3 ≤ x < 7 2 − 4832 945 x 3 + 58393 1008 x 2 − 52223 240 x + 2048227 7560 7 2 ≤ x < 4 35033 10080 x 3 − 75827 1680 x 2 + 981101 5040 x − 234149 840 4 ≤ x < 9 2 − 5261 3360 x 3 + 38509 1680 x 2 − 112487 1008 x + 30347 168 9 2 ≤ x < 5 1109 2520 x 3 − 24077 3360 x 2 + 78311 2016 x − 141311 2016 5 ≤ x < 11 2 − 19 280 x 3 + 1361 1120 x 2 − 14617 2016 x + 4151 288 11 2 ≤ x < 6 127 30240 x 3 − 55 672 x 2 + 5359 10080 x − 11603 10080 6 ≤ x < 13 2 − 1 30240 x 3 + 1 1440 x 2 − 7 1440 x + 49 4320 13 2 ≤ x < 7 0 otherwise {\displaystyle \psi _{C,4}(x)={\begin{cases}{\frac {1}{30240}}x^{3}&0\leq x<{\frac {1}{2}}\\-{\frac {127}{30240}}x^{3}+{\frac {2}{315}}x^{2}-{\frac {1}{315}}x+{\frac {1}{1890}}&{\frac {1}{2}}\leq x<1\\{\frac {19}{280}}x^{3}-{\frac {47}{224}}x^{2}+{\frac {2147}{10080}}x-{\frac {103}{1440}}&1\leq x<{\frac {3}{2}}\\-{\frac {1109}{2520}}x^{3}+{\frac {465}{224}}x^{2}-{\frac {32413}{10080}}x+{\frac {16559}{10080}}&{\frac {3}{2}}\leq x<2\\{\frac {5261}{3360}}x^{3}-{\frac {33463}{3360}}x^{2}+{\frac {42043}{2016}}x-{\frac {145193}{10080}}&2\leq x<{\frac {5}{2}}\\-{\frac {35033}{10080}}x^{3}+{\frac {93577}{3360}}x^{2}-{\frac {148517}{2016}}x+{\frac {216269}{3360}}&{\frac {5}{2}}\leq x<3\\{\frac {4832}{945}}x^{3}-{\frac {27691}{560}}x^{2}+{\frac {113923}{720}}x-{\frac {28145}{168}}&3\leq x<{\frac {7}{2}}\\-{\frac {4832}{945}}x^{3}+{\frac {58393}{1008}}x^{2}-{\frac {52223}{240}}x+{\frac {2048227}{7560}}&{\frac {7}{2}}\leq x<4\\{\frac {35033}{10080}}x^{3}-{\frac {75827}{1680}}x^{2}+{\frac {981101}{5040}}x-{\frac {234149}{840}}&4\leq x<{\frac {9}{2}}\\-{\frac {5261}{3360}}x^{3}+{\frac {38509}{1680}}x^{2}-{\frac {112487}{1008}}x+{\frac {30347}{168}}&{\frac {9}{2}}\leq x<5\\{\frac {1109}{2520}}x^{3}-{\frac {24077}{3360}}x^{2}+{\frac {78311}{2016}}x-{\frac {141311}{2016}}&5\leq x<{\frac {11}{2}}\\-{\frac {19}{280}}x^{3}+{\frac {1361}{1120}}x^{2}-{\frac {14617}{2016}}x+{\frac {4151}{288}}&{\frac {11}{2}}\leq x<6\\{\frac {127}{30240}}x^{3}-{\frac {55}{672}}x^{2}+{\frac {5359}{10080}}x-{\frac {11603}{10080}}&6\leq x<{\frac {13}{2}}\\-{\frac {1}{30240}}x^{3}+{\frac {1}{1440}}x^{2}-{\frac {7}{1440}}x+{\frac {49}{4320}}&{\frac {13}{2}}\leq x<7\\0&{\text{otherwise}}\end{cases}}} Compactly supported B-spline wavelet of order 5 The two-scale relation for the compactly supported B-spline wavelet of order 5 is
ψ C , 5 ( x ) = 1 5806080 [ N 5 ( 2 x ) − 507 N 5 ( 2 x − 1 ) + 17128 N 5 ( 2 x − 2 ) − 166304 N 5 ( 2 x − 3 ) + 748465 N 5 ( 2 x − 4 ) {\displaystyle \psi _{C,5}(x)={\frac {1}{5806080}}{\Big [}N_{5}(2x)-507N_{5}(2x-1)+17128N_{5}(2x-2)-166304N_{5}(2x-3)+748465N_{5}(2x-4)} − 1900115 N 5 ( 2 x − 5 ) + 2973560 N 5 ( 2 x − 6 ) − 2973560 N 5 ( 2 x − 7 ) + 1900115 N 5 ( 2 x − 8 ) {\displaystyle -1900115N_{5}(2x-5)+2973560N_{5}(2x-6)-2973560N_{5}(2x-7)+1900115N_{5}(2x-8)} − 748465 N 5 ( 2 x − 9 ) + 166304 N 5 ( 2 x − 10 ) − 17128 N 5 ( 2 x − 11 ) + 507 N 5 ( 2 x − 12 ) − N 5 ( 2 x − 13 ) ] {\displaystyle -748465N_{5}(2x-9)+166304N_{5}(2x-10)-17128N_{5}(2x-11)+507N_{5}(2x-12)-N_{5}(2x-13){\Big ]}} The closed form expression for compactly supported B-spline wavelet of order 5 is
ψ C , 5 ( x ) = { 1 8709120 x 4 0 ≤ x < 1 2 − 73 1244160 x 4 + 1 8505 x 3 − 1 11340 x 2 + 1 34020 x − 1 272160 1 2 ≤ x < 1 9581 4354560 x 4 − 19417 2177280 x 3 + 1303 96768 x 2 − 19609 2177280 x + 6547 2903040 1 ≤ x < 3 2 − 118931 4354560 x 4 + 366119 2177280 x 3 − 186253 483840 x 2 + 121121 311040 x − 427181 2903040 3 2 ≤ x < 2 759239 4354560 x 4 − 3146561 2177280 x 3 + 6466601 1451520 x 2 − 13202873 2177280 x + 26819897 8709120 2 ≤ x < 5 2 − 2980409 4354560 x 4 + 5183893 725760 x 3 − 13426333 483840 x 2 + 426589 8960 x − 12635243 414720 5 2 ≤ x < 3 7873577 4354560 x 4 − 16524079 725760 x 3 + 7385369 69120 x 2 − 17868671 80640 x + 497668543 290304 3 ≤ x < 7 2 − 14714327 4354560 x 4 + 108543091 2177280 x 3 − 56901557 207360 x 2 + 1454458651 2177280 x − 5286189059 8709120 7 2 ≤ x < 4 15619 3402 x 4 − 33822017 435456 x 3 + 15828929 32256 x 2 − 597598433 435456 x + 277413649 193536 4 ≤ x < 9 2 − 15619 3402 x 4 + 38150335 435456 x 3 − 20157247 32256 x 2 + 859841695 435456 x − 64472345 27648 9 2 ≤ x < 5 14714327 4354560 x 4 − 4466137 62208 x 3 + 165651247 290304 x 2 − 875490655 435456 x + 4614904015 1741824 5 ≤ x < 11 2 − 7873577 4354560 x 4 + 30717383 725760 x 3 − 179437319 483840 x 2 + 16606729 11520 x − 869722273 414720 11 2 ≤ x < 6 2980409 4354560 x 4 − 12698561 725760 x 3 + 16211669 96768 x 2 − 19138891 26880 x + 3289787993 2903040 6 ≤ x < 13 2 − 759239 4354560 x 4 + 10519741 2177280 x 3 − 10403603 207360 x 2 + 71964499 311040 x − 3481646837 8709120 13 2 ≤ x < 7 118931 4354560 x 4 − 1774639 2177280 x 3 + 630259 69120 x 2 − 14096161 311040 x + 245108501 2903040 7 ≤ x < 15 2 − 9581 4354560 x 4 + 21863 311040 x 3 − 407387 483840 x 2 + 9758873 2177280 x − 25971499 2903040 15 2 ≤ x < 8 73 1244160 x 4 − 4343 2177280 x 3 + 5273 207360 x 2 − 313703 2177280 x + 380873 1244160 8 ≤ x < 17 2 − 1 8709120 x 4 + 1 241920 x 3 − 1 17920 x 2 + 3 8960 x − 27 35840 17 2 ≤ x < 9 0 otherwise {\displaystyle \psi _{C,5}(x)={\begin{cases}{\frac {1}{8709120}}x^{4}&0\leq x<{\frac {1}{2}}\\-{\frac {73}{1244160}}x^{4}+{\frac {1}{8505}}x^{3}-{\frac {1}{11340}}x^{2}+{\frac {1}{34020}}x-{\frac {1}{272160}}&{\frac {1}{2}}\leq x<1\\{\frac {9581}{4354560}}x^{4}-{\frac {19417}{2177280}}x^{3}+{\frac {1303}{96768}}x^{2}-{\frac {19609}{2177280}}x+{\frac {6547}{2903040}}&1\leq x<{\frac {3}{2}}\\-{\frac {118931}{4354560}}x^{4}+{\frac {366119}{2177280}}x^{3}-{\frac {186253}{483840}}x^{2}+{\frac {121121}{311040}}x-{\frac {427181}{2903040}}&{\frac {3}{2}}\leq x<2\\{\frac {759239}{4354560}}x^{4}-{\frac {3146561}{2177280}}x^{3}+{\frac {6466601}{1451520}}x^{2}-{\frac {13202873}{2177280}}x+{\frac {26819897}{8709120}}&2\leq x<{\frac {5}{2}}\\-{\frac {2980409}{4354560}}x^{4}+{\frac {5183893}{725760}}x^{3}-{\frac {13426333}{483840}}x^{2}+{\frac {426589}{8960}}x-{\frac {12635243}{414720}}&{\frac {5}{2}}\leq x<3\\{\frac {7873577}{4354560}}x^{4}-{\frac {16524079}{725760}}x^{3}+{\frac {7385369}{69120}}x^{2}-{\frac {17868671}{80640}}x+{\frac {497668543}{290304}}&3\leq x<{\frac {7}{2}}\\-{\frac {14714327}{4354560}}x^{4}+{\frac {108543091}{2177280}}x^{3}-{\frac {56901557}{207360}}x^{2}+{\frac {1454458651}{2177280}}x-{\frac {5286189059}{8709120}}&{\frac {7}{2}}\leq x<4\\{\frac {15619}{3402}}x^{4}-{\frac {33822017}{435456}}x^{3}+{\frac {15828929}{32256}}x^{2}-{\frac {597598433}{435456}}x+{\frac {277413649}{193536}}&4\leq x<{\frac {9}{2}}\\-{\frac {15619}{3402}}x^{4}+{\frac {38150335}{435456}}x^{3}-{\frac {20157247}{32256}}x^{2}+{\frac {859841695}{435456}}x-{\frac {64472345}{27648}}&{\frac {9}{2}}\leq x<5\\{\frac {14714327}{4354560}}x^{4}-{\frac {4466137}{62208}}x^{3}+{\frac {165651247}{290304}}x^{2}-{\frac {875490655}{435456}}x+{\frac {4614904015}{1741824}}&5\leq x<{\frac {11}{2}}\\-{\frac {7873577}{4354560}}x^{4}+{\frac {30717383}{725760}}x^{3}-{\frac {179437319}{483840}}x^{2}+{\frac {16606729}{11520}}x-{\frac {869722273}{414720}}&{\frac {11}{2}}\leq x<6\\{\frac {2980409}{4354560}}x^{4}-{\frac {12698561}{725760}}x^{3}+{\frac {16211669}{96768}}x^{2}-{\frac {19138891}{26880}}x+{\frac {3289787993}{2903040}}&6\leq x<{\frac {13}{2}}\\-{\frac {759239}{4354560}}x^{4}+{\frac {10519741}{2177280}}x^{3}-{\frac {10403603}{207360}}x^{2}+{\frac {71964499}{311040}}x-{\frac {3481646837}{8709120}}&{\frac {13}{2}}\leq x<7\\{\frac {118931}{4354560}}x^{4}-{\frac {1774639}{2177280}}x^{3}+{\frac {630259}{69120}}x^{2}-{\frac {14096161}{311040}}x+{\frac {245108501}{2903040}}&7\leq x<{\frac {15}{2}}\\-{\frac {9581}{4354560}}x^{4}+{\frac {21863}{311040}}x^{3}-{\frac {407387}{483840}}x^{2}+{\frac {9758873}{2177280}}x-{\frac {25971499}{2903040}}&{\frac {15}{2}}\leq x<8\\{\frac {73}{1244160}}x^{4}-{\frac {4343}{2177280}}x^{3}+{\frac {5273}{207360}}x^{2}-{\frac {313703}{2177280}}x+{\frac {380873}{1244160}}&8\leq x<{\frac {17}{2}}\\-{\frac {1}{8709120}}x^{4}+{\frac {1}{241920}}x^{3}-{\frac {1}{17920}}x^{2}+{\frac {3}{8960}}x-{\frac {27}{35840}}&{\frac {17}{2}}\leq x<9\\0&{\text{otherwise}}\end{cases}}} Images of compactly supported B-spline wavelets B-spline wavelet of order 1 B-spline wavelet of order 2 B-spline wavelet of order 3 B-spline wavelet of order 4 B-spline wavelet of order 5
Battle-Lemarie wavelets The Battle-Lemarie wavelets form a class of orthonormal wavelets constructed using the class of cardinal B-splines. The expressions for these wavelets are given in the frequency domain; that is, they are defined by specifying their Fourier transforms. The Fourier transform of a function of t , say, F ( t ) {\displaystyle F(t)} F ^ ( ω ) {\displaystyle {\hat {F}}(\omega )}
Definition Let m be a positive integer and let N m ( x ) {\displaystyle N_{m}(x)} m . The Fourier transform of N m ( x ) {\displaystyle N_{m}(x)} N ^ m ( ω ) {\displaystyle {\hat {N}}_{m}(\omega )} ϕ m ( t ) {\displaystyle \phi _{m}(t)} m -th order Battle-Lemarie wavelet is that function whose Fourier transform is
ϕ ^ m ( ω ) = N ^ m ( ω ) ( ∑ k = − ∞ ∞ N ^ m ( ω + 2 π k ) 2 ) 1 / 2 . {\displaystyle {\hat {\phi }}_{m}(\omega )={\frac {{\hat {N}}_{m}(\omega )}{\left(\sum _{k=-\infty }^{\infty }\vert {\hat {N}}_{m}(\omega +2\pi k)\vert ^{2}\right)^{1/2}}}.} The m -th order Battle-Lemarie wavelet is the function ψ B L , m ( t ) {\displaystyle \psi _{BL,m}(t)}
ψ ^ B L , m ( ω ) = − e − i ω / 2 ϕ ^ m ( ω + 2 π ) ¯ ϕ ^ m ( ω 2 ) ϕ ^ m ( ω 2 + π ) ¯ {\displaystyle {\hat {\psi }}_{BL,m}(\omega )=-{\frac {e^{-i\omega /2}\,\,{\overline {{\hat {\phi }}_{m}(\omega +2\pi )}}\,\,{\hat {\phi }}_{m}\left({\frac {\omega }{2}}\right)}{\overline {{\hat {\phi }}_{m}\left({\frac {\omega }{2}}+\pi \right)}}}} References Further reading Amir Z Averbuch and Valery A Zheludev (2007). "Wavelet transforms generated by splines" (PDF) . International Journal of Wavelets, Multiresolution and Information Processing . 257 (5). Retrieved 21 December 2014 . Amir Z. Averbuch, Pekka Neittaanmaki, and Valery A. Zheludev (2014). Spline and Spline Wavelet Methods with Applications to Signal and Image Processing Volume I . Springer. ISBN 978-94-017-8925-7 {{cite book }}: CS1 maint: multiple names: authors list (link ) 




![[0,m]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1be36490b34e5d66e9566fa907c0e78fb3cd4540)











 대한 두 개의 양의 실수
대한 두 개의 양의 실수 










































 (가) 시퀀스
(가) 시퀀스 
 Kronecker 델타 함수
Kronecker 델타 함수 


 (는) 다음 방정식 시스템의 해결책이 된다.
(는) 다음 방정식 시스템의 해결책이 된다.

























 k
k



![[0,2m-1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a4e81b590032684241d6e9edff81e78992e983a)





 (와)
(와) 


![N_{m}(2x-l)=\sum _{{k=-\infty }}^{{\infty }}\left[a_{{m,l-2k}}N_{m}(x-k)+b_{{m,l-2k}}\psi _{{C,m}}(x-k)\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8de48d579d0c60f2aef862e9decacb08085aeea)










![303N_{3}(2x-4)-147N_{3}(2x-5)+29N_{3}(2x-6)-N_{3}(2x-7){\Big ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a26f3087ceb8326c2ae414e786e72f758af43b9)


![24264N_{4}(2x-5)+18482N_{4}(2x-6)-7904N_{4}(2x-7)+1677N_{4}(2x-8)-124N_{4}(2x-9)+N_{4}(2x-10){\Big ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/954587d75fd014fdc1674edda8f74c2ad842938f)



![-748465N_{5}(2x-9)+166304N_{5}(2x-10)-17128N_{5}(2x-11)+507N_{5}(2x-12)-N_{5}(2x-13){\Big ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22c1c022791fb4a2286a3b64e1dfac9b8233c78d)