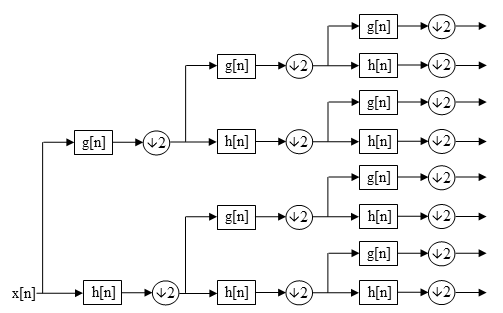
웨이블렛 패킷 분해

Wavelet packet decomposition

원래 WPD(Wavelet Packet Decisioning)라고도 하는 Optimal Subband Tree Structuring(SB-TS)으로 알려져 있으며(때로는 Wavelet Packets 또는 Subband Tree로만 알려져 있다)은 이산파형파형파형파형파형파형파형파형파형(DWT)보다 이산시간(sampled) 신호가 더 많은 필터를 통과하는 파형파형파형파형파형파형파형파형파형파형파형파형파형파형파형파형파형파형파형파형 변환이다.

소개

DWT에서 각 레벨은 이산 시간 로우 및 하이패스 4중 미러 필터를 통해 이전 파장 근사 계수(cAj)만 통과시켜 계산한다.[1][2]단, WPD에서는 세부사항(1-D 케이스의 경우j cD), cHj, cVj, cDj(2-D 케이스의 경우)와 근사계수가 모두 분해되어 완전한 이항 트리를 만든다.[3][2][4][5][6][7]

Wavelet 패킷 3단계 분해g[n]는 저역 근사 계수, h[n]는 고역 통과 상세 계수

분해 수준이 n개인 경우 WPD는 DWT에 대한 (n + 1) 집합과 반대로 2개의n 다른 계수(또는 노드) 집합을 생성한다.그러나 다운샘플링 공정으로 인해 전체 계수 수는 여전히 동일하고 중복성은 없다.

압축의 관점에서 표준 파장 변환은 저주파를 향해 2의 힘으로 증가하는 파장 베이스로 제한되기 때문에 최상의 결과를 만들어내지 못할 수 있다.또 다른 베이스 조합이 특정 신호에 대해 보다 바람직한 표현을 만들어 내는 것일 수 있다.[5] 서브밴드 트리 구조화에는 특정 비용함수(엔트로피, 에너지 압축 등)와 관련하여 가장 바람직한 데이터 표현을 제공하는 최적의 베이스 집합을 찾는 몇 가지 알고리즘이 있다.[1][2] 신호 처리 및 통신 분야에서는 에너지 압축(엔트로피), 하위 대역 상관 등을 포함한 관심 성능 지표와 관련하여 정기, 다이오드, 불규칙 등 다양한 종류의 서브밴드 트리(직교적 기반) 선택을 다루는 관련 연구가 있었다.[4] [6] [7]

이산 파장 변환 이론(시간 변수에서 연속)은 이산(시료 채취) 신호를 변환하는 근사치를 제공한다.이와는 대조적으로 이산 시간 서브밴드 변환 이론은 이미 샘플링된 신호의 완벽한 표현을 가능하게 한다.[5][8]

갤러리

  • Daubechies12-packet-functions.png
  • Daubechies12-packet-spectrum.png

적용들

사전 임상 진단에서 웨이블렛 패킷이 성공적으로 적용되었다.[9]

참조

  1. ^ a b Coifman RR & Wickerhauser MV, 1992.최상의 기반 선택을 위한 엔트로피 기반 알고리즘, 정보이론에 관한 IEEE 거래, 38(2)
  2. ^ a b c A.N. Akansu와 Y.류우, 신호 분해 기법 (초청 용지), 광학 공학 저널, 시각 통신 및 이미지 처리 특별호, vol.30, 페이지 912-920, 1991년 7월.
  3. ^ 도베키스, I. (1992년), 10개의 파도타기 강의, SIAM
  4. ^ a b H. 카글러, Y. 류, A.N.Akansu, 통계적으로 최적화된 PR-QMF 설계, Proc.SPIE 시각 통신 및 이미지 처리, vol. 1605, 페이지 86-94, 1991.
  5. ^ a b c A.N. Akansu와 R.A. Haddaddd, Multiresolution 신호 분해: 변환, 하위 밴드 및 웨이브릿.보스턴, MA: 아카데미 프레스, ISBN978-0-12-047141-6, 1992.
  6. ^ a b A. Benyassine과 A.N.아칸수, 이산 다복선 트랜스시버 , Proc를 위한 서브 채널의 성능 분석 및 최적 구조IEEE Proc.IEEE 국제회로 및 시스템 심포지엄(ISCAS), 페이지 1456-1459, 1995년 4월.
  7. ^ a b 엠빅토이 타즈베이 A.N.DSSSS 통신 시스템, IEEE Transfer를 위한 시간 주파수 조절기에서 Akansu, Adaptive Subband Transforms.1995년 11월, 제 43권, 페이지 2776-2782, 신호 처리.
  8. ^ A.N. Akansu, W.A. Serdijn, I.W. Selesnick, 신호 처리에서의 Wavelet Transforms: A Review of Emergining Applications, Physical Communication, Exvier, vol. 3, 1 페이지 1–18, 2010년 3월.
  9. ^ Zhang, Y.; Dong, Z. (2015). "Preclinical Diagnosis of Magnetic Resonance (MR) Brain Images via Discrete Wavelet Packet Transform with Tsallis Entropy and Generalized Eigenvalue Proximal Support Vector Machine (GEPSVM)". Entropy. 17 (4): 1795–1813. Bibcode:2015Entrp..17.1795Z. doi:10.3390/e17041795.

외부 링크

  • 파장 패킷 분해의 구현은 MATLAB 파장 툴박스에서 확인할 수 있다. [1].
  • R에 대한 구현은 Wavethresh 패키지 [2]에서 확인할 수 있다.
  • C++의 파장 패킷 코드와 함께 파장 패킷의 일러스트레이션 및 구현은 [3]에서 확인할 수 있다.
  • JWave: Haar, Daubechies, Coiflet, Legendre wavelet을 사용하여 1-D 및 2-D wavelet 패킷을 위한 자바에서의 구현.