리프팅 방식

리프팅 체계는 파장을 설계하고 이산 파장 변환(DWT)을 수행하는 기술이다.구현에서, 파장 변환을 수행하는 동안 이러한 단계를 병합하여 파장 필터를 설계하는 것이 가치 있는 경우가 많다.이를 제2세대 웨이블렛 변형이라고 한다.이 기술은 빔 스윌든스에 의해 소개되었다.^[1]

리프팅 체계는 유한 필터를 가진 모든 이산형 파장 변환을 일련의 초등 콘볼루션 연산자, 소위 리프팅 단계라고 불리는 것으로 인수하여 산술 연산의 수를 거의 2배 감소시킨다.신호 경계의 처리도 단순화된다.^[2]

이산형 파장 변환은 동일한 신호에 여러 필터를 별도로 적용한다.그것과는 대조적으로 리프팅 방식의 경우 신호가 지퍼처럼 나뉘어져 있다.그런 다음 분할된 신호에 걸쳐 일련의 콘볼루션-누적 연산을 적용한다.

기본 사항

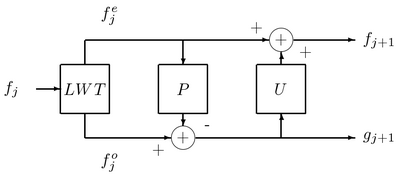
리프팅 구조에서 표현된 가장 단순한 버전의 전방 파장 변환은 위의 그림에 나타나 있다.${\displaystyle P}$ ${\displaystyle P}$은(는) 예측 단계를 의미하며$$, 이 단계는 별도로 고려될 것이다.예측 단계는 파월트 변환에서 파월트 함수를 계산한다.이것은 하이패스 필터다.업데이트 단계는 스케일링 기능을 계산하여 데이터의 버전을 부드럽게 만든다.

위에서 언급한 바와 같이, 리프팅 체계는 2차 파장을 이용하여 DWT를 수행하기 위한 대안 기법이다.리프팅 방식을 사용하여 DWT를 수행하기 위해서는 해당 리프팅 및 스케일링 단계가 2차 파장에서 도출되어야 한다.특정 웨이블렛의 분석 필터(${\displaystyle }$, ${\displaystyle h}$ ${\displaystyle g,h}$)는 먼저 다상 행렬로 작성된다.

${\displaystyle P(z)={\begin{bmatrix}h_{\text{ven}(z)&g_{\text{d}}}\h_{datad}}}{bmatrix},}$

여기서 ${\displaystyle \det }$ P${\displaystyle }$( ${\displaystyle z}$)${\displaystyle }$= ${\displaystyle {}^{}}$- ${\displaystyle m^{}}$ ${\$

다상 행렬은 분석 저역-통과 및 고역-통과 필터를 포함하는 2 × 2 행렬로, 각각 짝수 및 홀수 다항식 계수로 분할되어 정규화된다.여기서부터 행렬은 2 × 2 상각 및 하각 삼각형 행렬로 인수되며, 각 행렬은 대각선 입력이 1과 같다.상위 삼각형 행렬에는 예측 단계에 대한 계수가 포함되며, 하위 삼각 행렬에는 업데이트 단계에 대한 계수가 포함되어 있다.스케일링 단계 계수를 도출하기 위해 대각 값을 제외한 모든 0으로 구성된 행렬을 추출할 수 있다.다상 행렬은 양식에 요소화되어 있다.

${\displaystyle P(z)={\begin{bmatrix}a(1+z^{-1})\0&1\end{bmatrix}{bmatrix}}{\bgin{bmatrix}1&0\b(1+z)&1\end{bmatrix},},}$

$여기$서 ${\displaystyle a}$은(는) 예측 단계의 계수, $b{\displaystyle }$ ${\displaystyle b}$은(는) 업데이트 단계의 계수다.

확장 단계뿐만 아니라 여러 예측 및 업데이트 단계를 포함하는 더 복잡한 추출의 예가 아래에 나와 있다. ${\displaystyle a}$은(는) 첫 번째 예측 단계의 계수, $b{\displaystyle }$ ${\displaystyle b}$은(는) 첫 번째 업데이트 단계의 계수, $c{\displaystyle }$ ${\displaystyle c}$은(는) 두 번째 예측 단계의 계수다.p, $d{\displaystyle }$ ${\displaystyle d}$은(는) 두 번째 업데이트 단계의 계수, ${\displaystyle {k\mathrm{}}_{}}$ 1 ${\$1}은(는) 홀수치 스케일링 계수$$, $k{\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$}}은$$ 짝수 스케일링 계수:

${\displaystyle P(z)={\begin{bmatrix}1&a(1+z^{-1})\\0&1\end{bmatrix}}{\begin{bmatrix}1&0\\b(1+z)&1\end{bmatrix}}{\begin{bmatrix}1&c(1+z^{-1})\\0&1\end{bmatrix}}{\begin{bmatrix}1&0\\d(1+z)&1\end{bmatrix}}{\begin{bmatrix}k_{1}&0\\0&k_{2}\end{bmatrix}}.}$

행렬 이론에 따르면 다항식 항목과 결정 인수가 1인 행렬은 위에서 설명한 대로 인수될 수 있다.따라서 유한 필터를 사용한 모든 파장 변환은 일련의 리프팅 및 스케일링 단계로 분해될 수 있다.Daubechies와 Sweldens는 리프팅 스텝 추출에 대해 더 자세히 논의한다.^[3]

CDF 9/7 필터

CDF 9/7 변환을 수행하려면 예측 2단계와 업데이트 2단계 등 총 4단계 리프팅 단계가 필요하다.리프팅 계수화는 다음과 같은 필터링 단계로 이어진다.^[3]

${\displaystyle d_{l}=d_{l}+a(s_{l}+s_{l+1}),}$

${\displaystyle s_{l}=s_{l}+b(d_{l}+d_{l-1}),}$

${\displaystyle d_{l}=d_{l}+c(s_{l}+s_{l+1}),}$

${\displaystyle s_{l}=s_{l}+d(d_{l}+d_{l-1}),}$

${\displaystyle d_{l}=k_{1}d_{l}}$

${\displaystyle s_{l}=k_{2}s_{l}.}$

특성.

완벽한 재구성

리프팅 계획에 의한 모든 변환은 반전될 수 있다.모든 완벽한 재구축 필터 뱅크는 유클리드 알고리즘에 의해 리프팅 단계로 분해될 수 있다.즉, "리프팅-폐기 가능 필터 뱅크"와 "완벽한 재구축 필터 뱅크"는 같은 것을 의미한다.완벽한 재구축 필터 뱅크 2개마다 일련의 리프팅 단계에 의해 서로 변형될 수 있다.보다 잘 이해하기 위해 $P{\displaystyle }$ ${\displaystyle P}$과 Q ${\displaystyle Q}$이(가) 동일한$$ 결정 인자를 가진 다상 행렬인 경우 $P{\displaystyle }$ ${\displaystyle P}$에서 Q ${\displaystyle$ $Q$$}$까지의 리프팅 시퀀스는 게으른 다상 행렬 $I{\displaystyle }$ ${\displaystytyle$ I$}$에서 P${\displaystyle {}^{}}$- ${\displaystyle 1^{}q}$ {down Q {displaysty Q {\$displaystyption$ Q$}$까지와 동일하다$$.$e$ P$^{-1}\cdot$ Q$}$.

스피드업

속도 상승은 2배이다.이는 리프팅이 완벽한 재구축 필터 뱅크로 제한되기 때문에 가능한 것이다.즉, 리프팅은 완벽한 재구성에 의해 야기되는 중복을 어떻게든 짜내는 것이다.

변환은 메모리 오버헤드만 일정하게 유지한 채 입력 데이터의 메모리(제자리, 제자리)에서 즉시 수행될 수 있다.

비선형성

경련 수술은 다른 수술로 대체될 수 있다.완벽한 재구성을 위해 추가 작업의 역직성만 관련이 있다.이러한 방식으로 콘볼루션의 반올림 오류를 허용할 수 있으며 비트 실재 재구성이 가능하다.단, 비선형성에 의해 수치 안정성이 저하될 수 있다.이는 변환된 신호가 손실 압축에서처럼 처리되는 경우 반드시 존중되어야 한다.모든 재구성 가능한 필터 뱅크는 리프팅 스텝 측면에서 표현될 수 있지만, 리프팅 스텝에 대한 일반적인 설명은 웨이블렛 패밀리에 대한 설명에서 명확하지 않다.그러나, 예를 들어, 코헨-다우베키스의 단순한 경우–Feaubeau Wavelet, 리프팅 스텝에 대한 명시적인 공식이 있다.

사라지는 순간, 안정성 및 규칙성 증가

리프팅은 결과로 발생하는 바이오르토곤 파동의 소멸 순간 수를 증가시키기 위해 바이오르토곤 필터를 수정하며, 이들의 안정성과 규칙성을 희망한다.소멸 모멘트 수를 늘리면 신호가 규칙적인 지역의 파월 계수 진폭이 감소하여 표현이 더 희박해진다.그러나 리프팅으로 소멸 모멘트를 증가시키면 웨이블렛 지지대도 증가하는데, 이는 격리된 특이점에 의해 생성되는 큰 계수의 수를 증가시키는 역효과다.각 리프팅 단계는 필터 바이오토건성을 유지하지만 리에즈 경계와 그에 따른 웨이브렛 바이오토건 베이스의 안정성에 대한 제어력을 제공하지 않는다.기초가 직교하면 이중 기초는 원래 기초와 동일하다.따라서 원래 기준과 유사한 이중 기준을 갖는 것은 안정성의 지표다.그 결과, 이중 웨이블렛은 원래 웨이브만큼 소멸되는 모멘트가 많고 비슷한 크기의 지지대가 있을 때 일반적으로 안정성이 향상된다.리프팅 절차도 이중 웨이브의 소멸 모멘트를 증가시키는 이유다.이중 웨이블렛의 규칙성도 개선할 수 있다.리프팅 설계는 소멸 순간 수를 조정하여 계산한다.결과적인 이오르토곤 파장의 안정성과 규칙성은 최선의 것을 바라면서 후방으로 측정된다.이것이 이 웨이블렛 설계 절차의 주된 약점이다.

일반화 리프팅

일반화된 리프팅 방식은 조엘 솔레와 필리프 살렘비에가 개발해 솔레의 박사학위 논문에 실렸다.^[4]고전적인 리프팅 방식을 기본으로 하며, 제도 구조에 숨겨진 제약을 타파하여 일반화한다.고전적인 리프팅 방식은 다음과 같은 세 가지 종류의 조작을 가지고 있다.

1. 게으른 파장 변환은 $f{\displaystyle {}_{}^{}}$ ${\displaystyle j_{}^{}}$${\displaystyle {}_{}}$[ ${\displaystyle n_{}}$ ${\displaystyle ]}$ ${\displaystyle f_{j}[n$$]}$ 신호의 f j${\displaystyle {}_{}^{}}$[${\displaystyle n}$ ${\displaystyle ]}$로 표시된 홀수 샘플스 신호와$$ f ${\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}n}$ ${\displaystyle ]}$ ${\displaystyle f_{$$j}^{$$n]$로 표시된 짝수 샘플 신호의 두 개의 새로운 신호로$$ 나누어진다$.$
2. 예측 단계는 짝수 표본에 기초하여 홀수 표본에 대한 예측을 계산한다(또는 그 반대).이 예측은 홀수 샘플에서 차감되어 오류 $신호{\displaystyle {}_{}}$ g ${\displaystyle j_{}}$+ ${\displaystyle 1{}_{}}$[ n${\displaystyle }$] ${\displaystyle g_{j+1}[n]}$을(를) 생성한다$.$
3. 업데이트 단계는 서브샘플링 중에 일부 에너지가 제거된 상태에서 저주파 분기를 다시 보정한다.고전적인 리프팅의 경우, 이것은 다음 예측 단계를 위한 신호를 "준비"하기 위해 사용된다.예측된 홀수 ${\displaystyle {샘플}_{}}$ $g{\displaystyle {}_{}}$+ ${\displaystyle 1_{}}$[ ${\displaystyle n}$ ${\displaystyle ]}$ ${\displaystyle g_{j+1}[n]$을 사용하여$$ 짝수 샘플 f $j{\displaystyle {}_{}^{}}$ [n ${\displaystyle ]}$ $[\displaystyle f_{j}^{e}}}($또는 그 반대)을 준비한다.$$이 업데이트는 짝수 샘플에서 빼서 $f{\displaystyle {}_{}}$ ${\displaystyle j_{}}$+ ${\displaystyle 1_{}}$[ ${\displaystyle n}$ ${\displaystyle ]}$ $[\displaystyle f_{j+1}[n]}$로 표시된 신호를 생성한다$.$

그 계획은 구조상 되돌릴 수 없다.수신기에서 업데이트 단계는 짝수 샘플에 결과를 다시 추가한 다음 홀수 샘플에 추가하기 위해 정확하게 동일한 예측을 계산하는 것이 가능하다.원래 신호를 회복하려면 게으른 웨이브렛 변환을 뒤집어야 한다.일반화된 리프팅 방식은 동일한 세 가지 종류의 작업을 가지고 있다.그러나, 이 계획은 고전적인 리프팅을 제공하는 추가 굴절 제한을 피하며, 이것은 약간의 결과를 가져온다.예를 들어, 모든 단계의 설계는 계획 부정성을 보장해야 한다(추가 굴절 제한을 피할 경우 보장되지 않음).

정의

일반화된 리프팅 방식은 다음과 같은 규칙을 따르는 디아디드 변환이다.

1. 입력을 짝수 검체 스트림과 홀수 검체 스트림으로 분리한다.이것은 때때로 게으른 파도타기라고 불린다.
2. 예측 매핑을 계산한다.이 단계에서는 짝수(또는 그 반대)를 고려하여 홀수 표본을 예측하려고 한다.There is a mapping from the space of the samples in ${\displaystyle f_{j}^{e}[n]}$ to the space of the samples in ${\displaystyle g_{j+1}[n]}$. In this case the samples (from ${\displaystyle f_{j}^{e}[n]}$) chosen to be the reference for ${\displaystyle$$f_{j}^{o}[n]}$을(를) 컨텍스트라고 한다$$.그것은 다음과 같이 표현될 수 있다.

   ${\displaystyle \textstyle g_{j+1}[n]=P(f_{j}^{o}[n];f_{j}^{e}[n]]}}$

3. 업데이트 매핑을 계산한다.이 단계는 홀수 예측 표본을 고려하여 짝수 표본을 업데이트하려고 한다.만약 있다면 다음 예측 단계를 위한 일종의 준비일 것이다.그것은 다음과 같이 표현될 수 있다.

   ${\displaystyle \textstyle f_{j+1}[n]=U(f_{j}^{e}[n];g_{j+1}[n])}$

분명히 이러한 매핑은 어떤 함수가 될 수 없다.계획 자체의 반전성을 보장하기 위해 변환에 관련된 모든 매핑은 되돌릴 수 있어야 한다.매핑이 발생하여 유한 집합(분해된 경계 값 신호)에 도달하는 경우, 이 조건은 매핑이 주입(일 대 일)이라고 말하는 것과 같다.게다가, 만약 매핑이 한 세트에서 같은 카디널리티의 집합으로 간다면, 그것은 비굴해야 한다.

일반 리프팅 계획에서 이 단계를 매핑에 포함시킴으로써 추가/수축 제한을 피할 수 있다.이런 방식으로 고전적인 리프팅 체계가 일반화된다.

디자인

일부 설계는 예측 단계 맵핑을 위해 개발되었다.업데이트 단계가 정확히 어떻게 유용한지에 대한 답변이 남아 있기 때문에 업데이트 단계 설계는 철저히 검토되지 않았다.이 기법의 주요 적용 분야는 영상 압축이다.다음과 같은 몇 가지 흥미로운 언급이 있다.^[5][6][7][8]

적용들

• Wavelet은 정수를 정수에 매핑하는 변환
• 비트-정확한 재구성을^[9] 통한 푸리에 변환
• 필요한 횟수의 매끄러움 요소와 소멸 모멘트를 갖는 웨이블렛의 구성
• 주어진 패턴과^[10] 일치하는 웨이브렛의 구성
• JPEG 2000의 이산형 파장 변환 구현
• 데이터 기반 변환(예: 가장자리 회피 파장^[11])
• Wavelet 변환은 분리할 수 없는 격자(예: Quincunx 격자^[12] 위의 빨간색-검은색 물결표)에서 이루어진다.

참고 항목

• 암호학의 Feistel 체계는 추가와 함께 데이터를 나누고 함수 응용을 교대하는 것과 거의 동일한 개념을 사용한다.Feistel 체계와 리프팅 체계에서 이것은 대칭 en-decing과 디코딩에 사용된다.

참조

외부 링크

• 리프팅 계획 – 인수 알고리즘에 대한 간략한 설명
• 리프팅 시스템 소개