척도상관

통계에서 척도 상관 계수는 시계열과 같은 시간적 구성요소를 갖는 데이터에 적용할 수 있는 상관 계수의 한 형태다. 그것은 평균적인 단기 상관관계다. 신호에 여러 구성 요소(느리고 빠른)가 있는 경우, 느린 구성 요소의 기여를 무시한 채 신호의 빠른 구성 요소에 대해서만 스케일링된 상관 계수를 계산할 수 있다.^[1] 이 필터링과 같은 작동은 신호의 사인파 특성에 대해 가정할 필요가 없다는 장점이 있다.

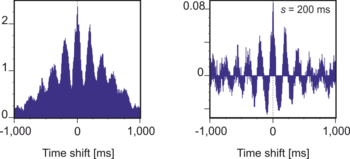
예를 들어 뇌신호 연구에서 연구자들은 고주파 성분(베타 및 감마 범위; 25-80Hz)에 관심이 많고 더 낮은 주파수 범위(알파, 세타 등)에는 관심이 없을 수 있다. 이 경우, 해당 주파수의 기간에 해당하는 분석의 척도, s를 선택하여 25Hz 이상의 주파수(예: 25Hz 진동에 대해 s = 40ms)에 대해서만 스케일 상관관계를 계산할 수 있다.

정의

두 신호 사이의 스케일 상관관계는 해당 신호의 짧은 세그먼트에서 계산된 평균 상관관계로 정의된다. 먼저 주어진 스케일 $s{\displaystyle }$ ${\displaystyle$ s}에$$대한 신호의 총 길이$$ $T{\displaystyle }$ ${\displaystyle$ T$}$에 $들어갈$ 수 있는 $세그먼트$ K ${\displaystyle$ K$}$의 수를 결정해야 한다$.$

${\displaystyle K=\operatorname {round} \left({\frac {T}{s}}}\오른쪽).}$

다음으로, $r{\displaystyle {}_{}}$ ${\displaystyle k_{}}$ ${\$${k$$}$가 $세그먼트$ k ${\$$displaystyle$ $k}$에 대한 피어슨의 상관 계수인 경우$,$ $전체{\displaystyle {\stackrel{}{}}_{}}$ ${\displaystyle {신호}_{}}$에 대한 스케일링 상관 계수는 다음과 같이 계산된다$.$

${\displaystyle {\r}_{s}={\frac {1}{K}\sum \limits _{k=1}^{K}r_{k}.}$

효율성

니콜리치 외 연구진은 자세한 분석에서 저속 구성 요소의 기여도가 감쇠되는 정도는 저울 선택, 저속 구성 요소와 고속 구성 요소 사이의 진폭 비율, 진동 주파수 차이 등 세 가지 요인에 따라 결정된다는 것을 보여주었다.^[1] 진동 주파수의 차이가 클수록 느린 성분의 기여도가 계산된 상관 계수에서 더 효율적으로 제거된다. 마찬가지로, 고속 구성요소에 비해 느린 구성요소의 검정력이 작을수록 상관관계가 더 잘 수행된다.

교차 상관에 적용

고주파 성분의 상관관계가 다른 시간적 지연에서 어떻게 변하는지 조사하기 위해 자동 및 교차 상관에 규모 상관관계를 적용할 수 있다. 매 시간 이동에 대한 교차 스케일-상관을 적절히 계산하려면 매 시간 이동 후에 신호를 다시 분할해야 한다. 즉, 분할을 적용하기 전에 신호는 항상 이동한다. 이후 축소된 상관관계는 시각적 피질에서 동기화 허브를 조사하기 위해 사용되어 왔다. 축소된 상관관계는 기능적 네트워크를 추출하는 데도 사용될 수 있다.^[3]

필터링 방법보다 장점

많은 경우 스펙트럼 방법에 기초한 신호 필터링보다 스케일링된 상관관계가 선호되어야 한다. 스케일링된 상관관계의 장점은 신호의 스펙트럼 특성(예: 신호의 사인파 모양)에 대한 가정을 하지 않는다는 것이다. 니콜리치 ^[1]외 느린 구성요소를 제거하기 위한 Wiener-Khinchin 정리의 사용이 스케일링된 상관관계를 통해 얻은 결과보다 낮다는 것을 보여주었다. 이러한 이점은 특히 신호가 비주기적이거나 뉴런 작용 전위가 감지된 타임스탬프와 같은 이산 이벤트로 구성되었을 때 명백해진다.

관련 방법

여러 척도에 걸친 상관 구조에 대한 자세한 통찰은 다중 솔루션 상관 관계 분석을 사용하여 시각화를 통해 제공할 수 있다.^[4]

참고 항목

• 자기 상관
• 일관성(신호 처리)
• 콘볼루션
• 상관 관계
• 교차상관
• 위상 상관 관계
• 스펙트럼 밀도
• 교차스펙트럼
• 비너-킨친 정리

참조

자유 출처

• 확장된 상호 상관 관계를 계산하기 위한 무료 소스 코드와 MATLAB용 인터페이스를 여기에서 다운로드할 수 있다: http://www.raulmuresan.ro/sources/corrlib/
• python의 간단한 데모 코드: https://github.com/dankonikolic/Scaled-Correlation