도베키 웨이브렛

이 글은 검증을 위해 추가 인용문이 필요합니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.출처 : 'Daubechies wavelet'– 뉴스 · 신문 · 서적 · 학자 · JSTOR (2009년 8월) (이 템플릿 메시지 삭제 방법 및 삭제 시기 확인)

Daubechies 20 2-d 웨이브렛(Wavelet Fn X 스케일링 Fn)

Daubechies 웨이브렛은 Ingrid Daubechies의 연구에 기초한 직교 웨이브렛 계열로 이산 웨이브렛 변환을 정의하며, 주어진 지지에서 최대 수의 소실 모멘트를 특징으로 한다.이 클래스의 각 웨이브릿 유형에는 직교 다중 해상도 분석을 생성하는 스케일링 함수(아버지 웨이브릿이라고 함)가 있습니다.

특성.

일반적으로 Daubechies 웨이브릿은 주어진 지지 폭(계수 수) ^[1]2A에 대해 가장 높은 수의 소실 모멘트를 가지도록 선택됩니다(이것은 최상의 평활성을 의미하지는 않습니다).탭 길이 또는 수를 사용하는 DN과 소실 모멘트의 수를 나타내는 dbA라는 두 가지 명명 방식이 사용되고 있습니다.D4와 db2는 같은 웨이브릿 변환입니다.

모멘트와 직교 조건의 대수 방정식의 가능한^A−1 2개의 해 중에서 스케일링 필터가 극한 위상을 가지는 것을 선택한다.웨이브릿 변환은 고속 웨이브릿 변환을 사용하여 쉽게 실행할 수 있습니다.도베키 웨이브렛은 신호의 자기 유사성이나 프랙탈 문제, 신호 불연속성 등 광범위한 문제를 해결하는데 널리 사용된다.

Daubechies 웨이브렛은 결과적인 스케일링 및 웨이브렛 함수의 관점에서 정의되지 않습니다.실제로 클로즈드 형식으로 기록할 수 없습니다.다음 그래프는 적절한 횟수만큼 역변환 [1 0 0 0 0 ...]으로 구성된 수치 기법인 캐스케이드 알고리즘을 사용하여 생성됩니다.

스케일링 및 웨이브릿 기능
상기 함수의 주파수 스펙트럼 진폭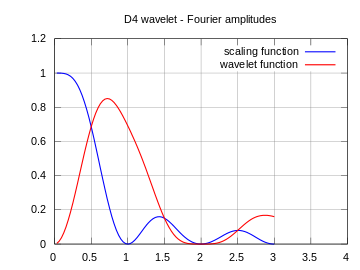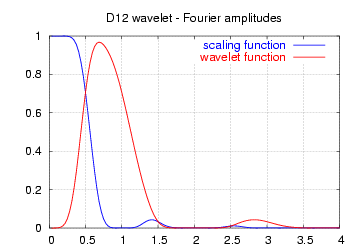

여기에 표시된 스펙트럼은 하이패스 및 로우패스 필터의 주파수 응답이 아니라 스케일링(파란색) 및 웨이브릿(빨간색) 함수의 연속 푸리에 변환의 진폭입니다.

도베키 직교 웨이브릿 D2–D20 response. db1–db10이 일반적으로 사용됩니다.지수 번호는 계수 N개의 수를 나타냅니다.각 웨이브릿은 계수의 절반에 해당하는 제로 모멘트 또는 소실 모멘트의 수를 가집니다.예를 들어 D2는 소실 모멘트가 1개, D4는 2개 등이다.소실 모멘트는 신호의 다항식 행동 또는 정보를 나타내는 웨이브릿 능력을 제한합니다.예를 들어 소실 모멘트가 1개인 D2는 하나의 계수 또는 일정한 신호 성분의 다항식을 쉽게 부호화할 수 있습니다.D4는 2개의 계수, 즉 상수와 선형 신호 성분으로 다항식을 부호화하며, D6은 3개의 다항식, 즉 상수와 선형 및 2차 신호 성분을 부호화한다.그럼에도 불구하고 이러한 신호 부호화 능력은 스케일 누출 현상과 변환 적용 중 이산 시프트 동작(아래)에서 발생하는 시프트 불변성의 결여의 영향을 받습니다.선형, 2차(예를 들어) 신호 성분을 나타내는 하위 시퀀스는 포인트가 시퀀스의 짝수 또는 홀수 위치에 정렬되는지 여부에 따라 변환에 의해 다르게 처리됩니다.시프트 불변성의 중요한 특성이 없기 때문에 시프트 불변(이산) 웨이브릿 변환의 여러 다른 버전이 개발되었습니다.

건설

이 섹션은 독자들에게 혼란스럽거나 불분명할 수 있습니다.특히, 정의되지 않은 수학 기호(예: a, p, P)가 있습니다. 섹션을 명확하게 하는 데 도움을 주세요. 토크 페이지에 이 건에 대한 논의가 있을 수 있습니다.(2019년 9월) (이 템플릿메시지 삭제 방법 및 삭제 시기 확인)

스케일링 시퀀스(저역 통과 필터)와 웨이브릿 시퀀스(밴드 통과 필터)(이 구조에 대한 자세한 내용은 직교 웨이브릿 참조)는 모두 합계가 2이고 제곱합이 2가 되도록 정규화됩니다.일부 응용 프로그램에서는 $합계$가 2$(\$인 것으로 정규화되어 있으므로 두 계수의 시퀀스 및 모든 시프트가 서로 직교합니다.

근사 순서 A를 갖는 직교 이산 웨이브릿 변환의 스케일링 시퀀스에 대한 일반 표현을 사용하여

${\displaystyle a(Z)=2^{1-A}(1+Z)^{A}p(Z),}$

N = 2A, p는 실계수를 가지며 p(1) = 1, deg(p) = A - 1일 때 직교성 조건을 다음과 같이 쓸 수 있다.

$(\displaystyle a(Z)a\left(Z^{-1}\right)+a(-Z)a\left(-Z^{-1}\right)=4,}$

또는 동등하게

${\displaystyle(2-X)^{A(X)+X^{A}P(2-X)=2^{A}\qquad(*),}$

로랑 다항식으로

$({displaystyle X:=flac {1}{2}}\left(2-Z-Z^{-1}\오른쪽)}$

모든 대칭 시퀀스를 $생성$하고 X${\displaystyle }$( -${\displaystyle Z}$ ) ${\displaystyle =2}$ -${\displaystyle X}$ (${\displaystyle Z}$)$$. { $displaystyle$ X ( - Z ) =$2$- X ($$Z ) } 또한 P(X)는 대칭 Laurent-polyomial을 나타냅니다.

${\displaystyle P(X(Z)=p(Z)p\left(Z^{-1}\오른쪽).}$

부터

${\displaystyle X(e^{iw})=1-\cos(w)}$

${\displaystyle p(e^{display}p(e^{-display})= p(e^{display})^{2}}$

P는 세그먼트 [0,2]에서 음이 아닌 값을 취한다.

식(*)은 각 A에 대해 하나의 최소 해를 가지며, 이는 X의 잘린 멱급수의 링에서 나눗셈으로 구할 수 있다.

${\displaystyle P_{A}(X)=\sum _{k=0}^{A-1}{\binom {A+k-1}{A-1}2^{-k}X^{k}.}$

분명히 이것은 (0,2)에 양의 값을 가지고 있습니다.

(*)에 대한 균질 방정식은 X = 1에 대해 반대칭이며, 따라서 일반 해를 가진다.

${{displaystyle X^{A}(X-1)R\left(X-1)^{2}\right),}$

R을 사용하여 실제 계수를 갖는 몇 가지 다항식을 사용합니다.그게 총액

$({displaystyle P(X)=P_{A}(X)+X^{A}(X-1)R\left((X-1)^{2}\오른쪽)}$

[0,2] 구간에서 음이 아니어야 하며 이는 R 계수에 대한 일련의 선형 제한으로 해석된다.구간 [0,2]의 P 값은 $일정량{\displaystyle {\mathrm{}}^{}}$ 4${\displaystyle A^{}}$ -${\displaystyle {}^{}{r}^{}}$ ,$${$displaystyle$ 4$^{A-r}$에 의해 제한되며, 부등식 조건이 무한히 많은 선형 프로그램에서 r 결과를 최대화한다$$.

해결하려면

${\displaystyle P(X(Z)=p(Z)p\left(Z^{-1}\오른쪽)}$

p는 스펙트럼 인수분해 반응이라고 불리는 기술을 사용한다.Fejér-Riesz-algorithm.다항식 P(X)는 선형 인자로 분할됩니다.

$\displaystyle P(X)=(X-\mu _{1})\cdots(X-\mu _{N}),\qquad N=A+1+2\deg(R)}$

각 선형 인수는 로랑 다항식을 나타낸다.

${\displaystyle X(Z)-\mu =-{\frac {1}{2}}Z+1-\mu-{\frac {1}{-1}Z^{-1}$

두 개의 선형 인자로 나눌 수 있습니다.두 선형 요인 중 하나를 p(Z)에 할당할 수 있으므로 두 개의 가능한 솔루션을 얻을^N 수 있습니다.극단 위상의 경우 단위 원 내부 또는 위에 p(Z)의 모든 복잡한 루트를 가진 것을 선택하므로 실재한다.

Daubechies 웨이브릿 변환에는 한 쌍의 선형 필터가 사용됩니다.쌍의 각 필터는 직교 미러 필터여야 합니다.직교 미러 필터 특성을 이용하여 선형 $필터{\displaystyle {}_{}}$ $(\$})의$$ 계수를 풀면 4차 필터의 계수 값은 다음과 같다.

${\displaystyle c_{0}=syslogfrac {1+{\syslogrt {3}},\syslogc c_{1}=syslogfrac {3+{\syslogrt {3}},\syslogc_{2}=syslogfrac {3-{\syslogrt {3}}}, {syslog}}}$

가장 낮은 근사 순서의 스케일링 시퀀스

아래는 D2-20의 스케일링 함수에 대한 계수입니다.웨이브릿 계수는 스케일링 함수 계수의 순서를 반대로 한 다음 매초마다 $D4$ 웨이브릿${\$ {-0.$1830127$, -0.3169873, 1.1830127, -0.6830127} $$기호를 반대로 하여 도출됩니다.이는 수학적으로 b ${\displaystyle k_{}}$ $=$( -${\displaystyle {}^1}$) ${\displaystyle {}^{}{}_{}}$ a${\displaystyle N_{}}$ -${\displaystyle 1_{}}$ -$$ { $displaystyle$ b$_$ { k } $a$_ { N - 1 - $k$} { k } a _ { N - 1 -$$k }처럼 보입니다.여기서 k는 웨이브릿 시퀀스의 계수, b는 스케일링 시퀀스의 계수입니다.N은 웨이브릿 지수, 즉 D2의 경우 2이다.

구조의 일부는 또한 바이오직교 코헨-도베치를 도출하는 데 사용된다.–Feau Wavelet(CDF)

실행

Mathematica 등의 소프트웨어는 Daubechies wavelet을^[2] 직접 지원하지만 MATLAB(이 경우 Daubechies 4)에서는 기본 구현이 가능합니다.이 실장에서는 기간화를 사용하여 유한 길이 신호의 문제를 처리합니다.그 밖에도 보다 정교한 방법을 사용할 수 있지만 변환된 신호의 맨 끝에만 영향을 미치기 때문에 이러한 방법을 사용할 필요가 없는 경우가 많습니다.주기화는 MATLAB 벡터 표기법에 의한 정방향 변환에서 직접 수행되며 역방향 변환에서는 다음을 사용하여 수행됩니다.circshift()기능:

변환, D4

분석 대상 신호로는 짝수 원소의 열 벡터인 S가 미리 정의되어 있다고 가정한다.D4 계수는 [1 + 33, 3 + 33, 3 - 33, 1 - 33]/4입니다.

N = 길이(S); s1 = S(1:2:N - 1) + sqrt(3) * S(2:2:N); d1 = S(2:2:N) - sqrt(3) / 4 * s1 - (sqrt(3) - 2) / 4 * [s1(N / 2); s1(1:N / 2 - 1)]; s2 = s1 - [d1(2:N / 2); d1(1)]; s = (sqrt(3) - 1) / sqrt(2) * s2; d = - (sqrt(3) + 1) / sqrt(2) * d1; 

역변환, D4

d1 = d * ((sqrt(3) - 1) / sqrt(2)); s2 = s * ((sqrt(3) + 1) / sqrt(2)); s1 = s2 + 순환 시프트(d1, - 1); S(2:2:N) = d1 + sqrt(3) / 4 * s1 + (sqrt(3) - 2) / 4 * 순환 시프트(s1, 1); S(1:2:N - 1) = s1 - sqrt(3) * S(2:2:N); 

이항 QMF

1990년에 Ali Akansu에 의해 이항 직교 미러 필터 뱅크(이항 QMF)가 Daubechies 웨이브렛 필터와 동일하다는 것이 입증되었으며, 그 성능은 이산 시간 신호 처리 관점에서 ^[3][4]알려진 부분 공간 솔루션 중에서 순위가 매겨졌다.이는 1987년 ^[5][6]수정 에르미트 변환(MHT)의 개발을 이끈 이항 계수 및 에르미트 다항식에 대한 이전 연구의 연장선이었다.이항 QMF 필터의 크기 제곱 함수는 연속 ^[7][8]영역의 웨이브릿 규칙성과 관련된 2-밴드 완전 재구성 QMF(PR-QMF) 설계 공식에서 고유한 최대 평탄 함수입니다.

「 」를 참조해 주세요.

• 고속 웨이브릿 변환

레퍼런스

외부 링크

Wikimedia Commons에는 Daubechies 웨이브렛과 관련된 미디어가 있습니다.

• Ingrid Daubechies:1992년 SIAM 웨이브릿 10강좌
• 프로시저 1차 NJWavelet, Subbands and Transforms에 관한 IT 심포지엄, 1990년 4월
• Akansu, Ali N.; Haddad, Richard A. (1992), Multiresolution Signal Decomposition: Transforms, Subbands, and Wavelets, Boston, MA: Academic Press, ISBN 978-0-12-047141-6
• A.N. Akansu, 필터 뱅크 및 Wavelet 신호 처리: A.N. Akansu, Critical Review, Pro.SPIE 비디오 통신 및 의료 애플리케이션용 PACS(초대 문서), 페이지 330-341, vol. 1977, 베를린, 1993년 10월.
• Carlos Cabrelli, Ursula Molter: "일반화된 자기 유사성", 수학 분석 및 응용 저널, 230: 251–260, 1999.
• 웨이브릿 하드웨어 구현
• 를 클릭합니다"Daubechies wavelets", Encyclopedia of Mathematics, EMS Press, 2001 [1994].
• I. 카플란, Daubechies D4 웨이브릿 트랜스폼
• Jensen; la Cour-Harbo (2001). Ripples in Mathematics. Berlin: Springer. pp. 157–160. ISBN 3-540-41662-5.
• 지안홍(재키) Shen and Gilbert Stren, Applied and Computational Harmonic Analysis, 5(3), Daubechies 필터의 점근율, 스케일링 함수 및 웨이브렛.